2.1.1: Introducción a las fracciones y números mixtos
- Page ID
- 111426
- Identificar el numerador y denominador de una fracción.
- Representar una fracción como parte de un todo o parte de un conjunto.
Introducción
Muchos problemas en las matemáticas tratan con números enteros, que se utilizan para contar unidades enteras de cosas. Por ejemplo, se puede contar a los estudiantes en un salón de clases y el número de billetes de dólar. Se necesitan otros tipos de números para describir unidades que no son enteras. Por ejemplo, un acuario podría estar parcialmente lleno. Un grupo puede tener una reunión, pero sólo algunos de los integrantes están presentes.
Las fracciones son números que se utilizan para referirse a una parte de un todo. Esto incluye medidas que no se pueden escribir como números enteros. Por ejemplo, el ancho de un trozo de papel de cuaderno es de más de 8 pulgadas pero menos de 9 pulgadas. La parte de más de 8 pulgadas se escribe como una fracción. Aquí, investigará cómo se pueden escribir y usar fracciones para representar cantidades que son partes del todo.
Identificación de Numeradores y Denominadores
Un todo se puede dividir en partes de igual tamaño. En el siguiente ejemplo, un rectángulo se ha dividido en ocho cuadrados iguales. Cuatro de estos ocho cuadrados están sombreados.
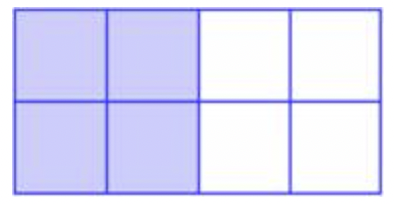
El área sombreada puede ser representada por una fracción. Una fracción se escribe verticalmente como dos números con una línea entre ellos.
El denominador (el número inferior) representa el número de partes iguales que componen el conjunto. El numerador (el número superior) describe el número de partes que está describiendo. Por lo que volviendo al ejemplo anterior, el rectángulo se ha dividido en 8 partes iguales, y 4 de ellas han sido sombreadas. Puedes usar la fracción\(\ \frac{4}{8}\) para describir la parte sombreada del conjunto.
En\(\ \frac{4}{8}\), el 4 es el numerador y cuenta cuántas partes están sombreadas. El 8 es el denominador y cuenta cuántas partes se requieren para hacer el conjunto.
Partes de un juego
El modelo rectangular anterior proporciona una buena introducción básica a las fracciones. No obstante, ¿qué haces con situaciones que no se pueden modelar tan fácilmente sombreando parte de una figura? Por ejemplo, piensa en la siguiente situación:
Marc trabaja como Gerente de Aseguramiento de Calidad en una planta automotriz. Cada hora, inspecciona 10 autos;\(\ \frac{4}{5}\) de esos pasan inspección.
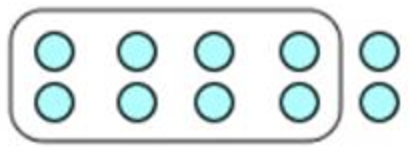
En este caso, 10 autos conforman a todo el grupo. Cada automóvil se puede representar como un círculo, como se muestra a continuación.
Para mostrar\(\ \frac{4}{5}\) de todo el grupo, primero hay que dividir todo el grupo en 5 partes iguales. (Esto lo sabes porque la fracción tiene un denominador de 5.)
Para mostrar\(\ \frac{4}{5}\), círculo 4 de las partes iguales.
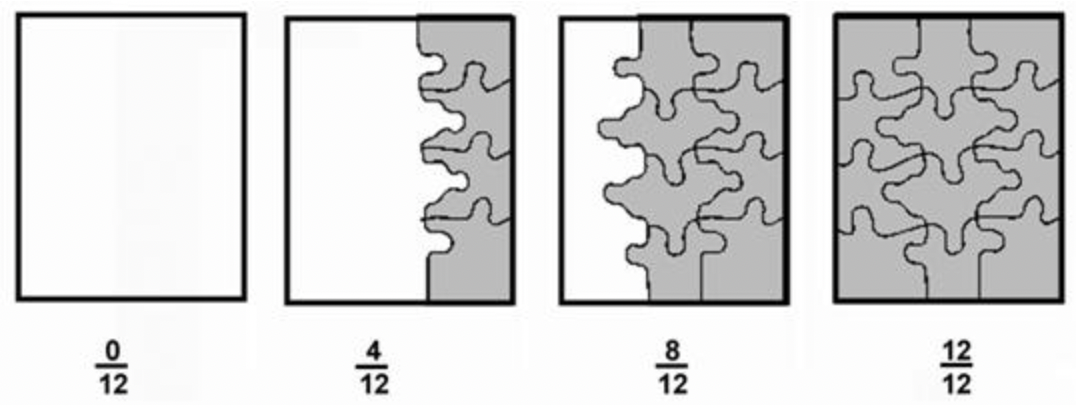
Aquí hay otro ejemplo. Imagina que Aneesh está armando un rompecabezas hecho de 12 piezas. Al principio, ninguna de las piezas se ha puesto en el rompecabezas. Esto quiere decir que\(\ \frac{0}{12}\) del rompecabezas está completo. Aneesh luego junta cuatro piezas. El rompecabezas está\(\ \frac{4}{12}\) completo. Pronto, agrega cuatro piezas más; 8 de 12 piezas ahora están conectadas. Esta fracción se puede escribir como\(\ \frac{8}{12}\). Por último, Aneesh agrega cuatro piezas más. El rompecabezas es entero, usando las 12 piezas. La fracción se puede escribir como\(\ \frac{12}{12}\).
Tenga en cuenta que el número en el denominador no puede ser cero. El denominador dice cuántas partes componen el conjunto. Entonces si este número es 0, entonces no hay partes y por lo tanto no puede haber entero.
El numerador puede ser cero, ya que dice cuántas partes estás describiendo. Observe que en el ejemplo de rompecabezas anterior, puede usar la fracción\(\ \frac{0}{12}\) para representar el estado del rompecabezas cuando se hayan colocado 0 piezas.
Las fracciones también se pueden utilizar para analizar datos. En la tabla de datos a continuación, 3 de cada 5 tiradas de una moneda surgieron cabezas, y 2 de 5 tiradas llegaron a la cola. Del número total de tiradas de monedas, la porción que era cabezas se puede escribir como\(\ \frac{3}{5}\). La porción que era colas se puede escribir como\(\ \frac{2}{5}\).
| Toss de monedas | Resultado |
| 1 | Cabezales |
| 2 | Tails |
| 3 | Cabezales |
| 4 | Cabezales |
| 5 | Tails |
Sophia, Daphne y Charlie están participando en una carrera de relevos para recaudar dinero para la caridad. Primero, Sophia correrá 2 millas. Entonces, Daphne correrá 5 millas. Por último, Charlie terminará la carrera corriendo 3 millas. ¿Qué fracción de la carrera correrá Daphne?
- 5 millas
- \(\ \frac{5}{10}\)
- \(\ \frac{2}{5}\)
- \(\ \frac{5}{3}\)
- Contestar
-
- Incorrecto. Daphne correrá 5 millas, pero eso no indica la parte fraccionaria de la carrera que correrá. Para encontrar la fracción, primero encuentra toda la longitud de la carrera combinando las distancias que correrán las tres personas: 2+5+3=10. Entonces considera la distancia que recorrerá Daphne. La respuesta correcta es\(\ \frac{5}{10}\).
- Correcto. Toda la carrera tiene 10 millas de largo, y Daphne correrá 5 millas. Esto significa que correrá\(\ \frac{5}{10}\) de la carrera.
- Incorrecto. Para encontrar la fracción, primero encuentra toda la longitud de la carrera combinando las distancias que correrán las tres personas: 2+5+3=10. Entonces considera la distancia que recorrerá Daphne. La respuesta correcta es\(\ \frac{5}{10}\).
- Incorrecto. Para encontrar la fracción, primero encuentra toda la longitud de la carrera combinando las distancias que correrán las tres personas: 2+5+3=10. Entonces considera la distancia que recorrerá Daphne. La respuesta correcta es\(\ \frac{5}{10}\).
Partes de un Todo
El concepto de “partes de un todo” se puede modelar con pizzas y rebanadas de pizza. Por ejemplo, imagina que una pizza se corta en 4 trozos, y alguien toma 1 pieza. Ahora,\(\ \frac{1}{4}\) de la pizza se ha ido y\(\ \frac{3}{4}\) permanece. Obsérvese que ambas fracciones tienen un denominador de 4, lo que hace referencia al número de rebanadas en las que se ha cortado la pizza entera.
Joaquim prepara un pastel de arándanos para una cena compartida. El pastel total se corta en 6 rebanadas iguales. Después de que todos coman postre, solo queda una rebanada del pastel. ¿Qué fracción del pastel queda?
Solución
| \(\ \frac{?}{6}\) | El pastel se cortó en seis rebanadas iguales, por lo que el denominador de la fracción será 6. |
| \(\ \frac{1}{6}\) | Sólo queda 1 rebanada, por lo que el numerador de la fracción será 1. |
| \(\ \frac{1}{6}\)de los restos de pastel. |
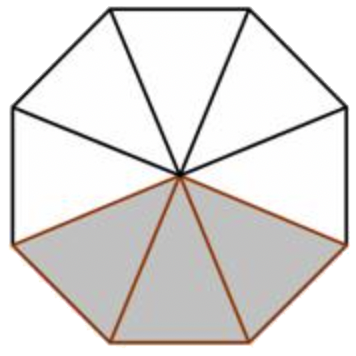Escribe una fracción para representar la porción del octágono que no está sombreada.
Solución
| \(\ \frac{?}{8}\) | El octágono tiene ocho secciones iguales, por lo que el denominador de la fracción será 8. |
| \(\ \frac{5}{8}\) | Cinco secciones no están sombreadas, por lo que el numerador de la fracción será 5. |
| \(\ \frac{5}{8}\)del octágono no está sombreado. |
Contextos de medición
Se puede usar una fracción para representar la cantidad en un contenedor. Esta taza medidora se\(\ \frac{3}{4}\) llena con un líquido. Tenga en cuenta que si la copa estuviera\(\ \frac{4}{4}\) llena, sería una taza entera.
También puedes usar fracciones para medir el largo, ancho o alto de algo que no sea una unidad completa. Usando una regla de 12 pulgadas, se mide un caparazón que mide 6 pulgadas de largo. Sabes que 12 pulgadas equivale a un pie. Entonces, la longitud de este caparazón es\(\ \frac{6}{12}\) de un pie; la regla de 12 pulgadas es el “todo”, y la longitud del caparazón es la “parte”.
¿Qué fracción representa la porción de la forma que está sombreada?
- \(\ \frac{8}{7}\)
- \(\ \frac{7}{8}\)
- Contestar
-
- Incorrecto. El número total de partes que componen el conjunto, 8, es el denominador. Ese es el número por debajo de la barra de fracciones. El número de partes sombreadas, 7, es el numerador. Ese es el número por encima de la barra de fracciones. La respuesta correcta es\(\ \frac{7}{8}\).
- Correcto. El número total de partes que componen el conjunto, 8, es el denominador (por debajo de la barra de fracción). El número de partes sombreadas, 7, es el numerador (por encima de la barra de fracción).
Resumen
Las fracciones se utilizan para representar partes de un todo. Puede usar fracciones al describir sustancias, cantidades o diagramas que no estén completos. También se utilizan fracciones para describir números de personas u objetos que no conforman un grupo completo. Las fracciones se escriben con numerador y denominador. El numerador (por encima de la barra de fracciones) indica el número de partes que se describen, y el denominador (por debajo de la barra de fracciones) indica el número de partes que componen el todo.