4.2.1: Comprender las proporciones

Última actualización
Guardar como PDF

Page ID: 111187

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Determinar si una proporción es verdadera o falsa.
Encontrar un desconocido en una proporción.
Resolver problemas de aplicación usando proporciones.

Introducción

Una verdadera proporción es una ecuación que establece que dos proporciones son iguales. Si conoces una proporción en una proporción, puedes usar esa información para encontrar valores en la otra proporción equivalente. Usar proporciones puede ayudarte a resolver problemas como aumentar una receta para alimentar a una multitud más grande de personas, crear un diseño con ciertas características consistentes o ampliar o reducir una imagen a escala.

Por ejemplo, imagina que quieres ampliar una fotografía de 5 pulgadas por 8 pulgadas para que se ajuste a un marco de madera que hayas comprado. Si quieres que el borde más corto de la foto ampliada mida 10 pulgadas, ¿cuánto tiempo tiene que ser la foto para que la imagen se escale correctamente? Puede configurar una proporción para determinar la longitud de la foto ampliada.

Determinar si una proporción es verdadera o falsa

Una proporción suele escribirse como dos fracciones equivalentes. Por ejemplo:

$\ \frac{12 \text { inches }}{1 \text { foot }}=\frac{36 \text { inches }}{3 \text { feet }}$

Observe que la ecuación tiene una relación a cada lado del signo igual. Cada relación compara las mismas unidades, pulgadas y pies, y las relaciones son equivalentes porque las unidades son consistentes, y$\ \frac{12}{1}$ es equivalente a$\ \frac{36}{3}$.

Las proporciones también podrían comparar dos proporciones con las mismas unidades. Por ejemplo, Juanita tiene dos recipientes de mezcla de limonada de diferentes tamaños. Ella quiere compararlos. Ella podría establecer una proporción para comparar el número de onzas en cada recipiente con el número de porciones de limonada que se pueden hacer de cada recipiente.

$\ \frac{40 \text { ounces }}{84 \text { ounces }}=\frac{10 \text { servings }}{21 \text { servings }}$

Dado que las unidades para cada ratio son las mismas, puedes expresar la proporción sin las unidades:

$\ \frac{40}{84}=\frac{10}{21}$

Al utilizar este tipo de proporción, es importante que los numeradores representen la misma situación. En el ejemplo anterior representan 40 onzas por 10 raciones. Los denominadores también deben representar la misma situación, que es onzas para raciones.

Juanita también podría haber establecido la proporción para comparar las proporciones de los tamaños de los contenedores con el número de porciones de cada contenedor.

$\ \frac{40 \text { ounces }}{10 \text { servings }}=\frac{84 \text { ounces }}{21 \text { servings }}$

En ocasiones necesitarás averiguar si dos ratios son, de hecho, una proporción verdadera o falsa. A continuación se muestra un ejemplo que muestra los pasos para determinar si una proporción es verdadera o falsa.

Ejemplo

¿La proporción es verdadera o falsa?

$\ \frac{100 \text { miles }}{4 \text { gallons }}=\frac{50 \text { miles }}{2 \text { gallons }}$

Solución

millas (consultar)

Las unidades son consistentes a través de los numeradores.

galones (check)

Las unidades son consistentes a través de los denominadores.

Escribe cada proporción en la forma más simple.

\ (\\ begin {array} {l}
\ frac {100\ div 4} {4\ div 4} =\ frac {25} {1}\
\ frac {50\ div 2} {2\ div 2} =\ frac {25} {1}\
\ frac {25} {1} {1} =\ frac {25} {1}
\ end {array}\)

Dado que las fracciones simplificadas son equivalentes, la proporción es verdadera.

La proporción es cierta.

Identificar proporciones verdaderas

Para determinar si una proporción compara proporciones iguales o no, puedes seguir estos pasos.

Verifique para asegurarse de que las unidades en las relaciones individuales sean consistentes ya sea vertical u horizontalmente. Por ejemplo,$\ \frac{\text { miles }}{\text { hour }}=\frac{\text { miles }}{\text { hour }}$ o$\ \frac{\text { miles }}{\text { miles }}=\frac{\text { hour }}{\text { hour }}$ son configuraciones válidas para una proporción.
Exprese cada proporción como una fracción simplificada.
Si las fracciones simplificadas son las mismas, la proporción es verdadera; si las fracciones son diferentes, la proporción es falsa.

En ocasiones es necesario crear una proporción antes de determinar si es verdad o no. A continuación se muestra un ejemplo.

Ejemplo

Una oficina cuenta con 3 impresoras para 18 computadoras. Otra oficina cuenta con 20 impresoras para 105 computadoras. ¿La relación entre impresoras y computadoras es la misma en estas dos oficinas?

Solución

$\ \frac{\text { printers }}{\text { computers }}=\frac{\text { printers }}{\text { computers }}$	Identificar la relación.
$\ \frac{3 \text { printers }}{18 \text { computers }}=\frac{20 \text { printers }}{105 \text { computers }}$	Escribe proporciones que describan cada situación, y ponerlas iguales entre sí.
Impresoras (check)	Verifique que las unidades en los numeradores coincidan.
Computadoras (check)	Verifique que las unidades en los denominadores coincidan. Simplifica cada fracción y determina si son equivalentes.
\ (\\ begin {array} {c} \ frac {3\ div 3} {18\ div 3} =\ frac {1} {6}\ \ frac {20\ div 5} {105\ div 5} =\ frac {4} {21}\ \ frac {1} {6}\ neq\ frac {4} {21} \ end {array}\)	Dado que las fracciones simplificadas no son iguales (designadas por el$\ \neq$ signo), la proporción no es cierta.

La relación entre impresoras y computadoras no es la misma en estas dos oficinas.

Hay otra manera de determinar si una proporción es verdadera o falsa. Este método se llama “encontrar el producto cruzado” o “multiplicación cruzada”.

Para cruzar multiplicar, multiplicas el numerador de la primera relación en la proporción por el denominador de la otra proporción. Después multiplica el denominador de la primera relación por el numerador de la segunda proporción en la proporción. Si estos productos son iguales, la proporción es verdadera; si estos productos no son iguales, la proporción no es cierta.

Esta estrategia para determinar si una proporción es verdadera se llama multiplicación cruzada porque el patrón de la multiplicación parece una “x” o un entrecruzamiento. A continuación se muestra un ejemplo de encontrar un producto cruzado, o multiplicación cruzada.

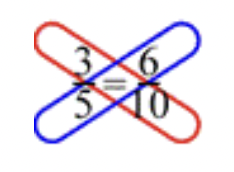
$Screen Shot 2021-04-29 en 3.54.27 PM.png$

En este ejemplo, multiplicas$\ 3 \cdot 10=30$, y luego multiplicas$\ 5 \cdot 6=30$. Ambos productos son iguales, por lo que la proporción es cierta.

A continuación se muestra otro ejemplo de determinar si una proporción es verdadera o falsa mediante el uso de productos cruzados.

Ejemplo

¿La proporción es verdadera o falsa?

$\ \frac{5}{6}=\frac{9}{8}$

Solución

$captura de pantalla 2021-04-29 en 3.png$	Identificar la relación cruzada de productos.
\ (\\ begin {array} {l} 5\ cdot 8=40\\ 6\ cdot 9=54 \ end {array}\)	Utilice productos cruzados para determinar si la proporción es verdadera o falsa.
$\ 40 \neq 54$	Dado que los productos no son iguales, la proporción es falsa.

La proporción es falsa.

Ejercicio

¿La proporción es$\ \frac{3}{5}=\frac{24}{40}$ verdadera o falsa?

Cierto
Falso

Contestar

Correcto. Usando productos cruzados, lo encuentras$\ 3 \cdot 40=120$ y$\ 5 \cdot 24=120$, así los productos cruzados son iguales y la proporción es cierta.
Incorrecto. Los productos cruzados son iguales, por lo que la proporción es cierta. La respuesta correcta es cierta.

Encontrar una cantidad desconocida en una proporción

Si sabes que la relación entre cantidades es proporcional, puedes usar proporciones para encontrar cantidades faltantes. A continuación se muestra un ejemplo.

Ejemplo

Resolver por la cantidad desconocida,$\ n$.

$\ \frac{n}{4}=\frac{25}{20}$

Solución

$\ 20 \cdot n=4 \cdot 25$	Multiplicar cruz.
$\ 20 n=100$	Estás buscando un número que al multiplicarlo por 20 obtienes 100.
\ (\\ begin {array} {r} 5\\\\ 20\ longdiv {100} \ end {array}\)	Puedes encontrar este valor dividiendo 100 por 20.

$\ n=5$

Ahora volvamos al ejemplo original. Imagina que quieres ampliar una fotografía de 5 pulgadas por 8 pulgadas para hacer la longitud 10 pulgadas y mantener la proporción del ancho a la longitud igual. Se puede configurar una proporción para determinar el ancho de la foto ampliada.

$Screen Shot 2021-04-29 a las 10.39.23 PM.png$

Ejemplo

Encuentra la longitud de una fotografía cuyo ancho es de 10 pulgadas y cuyas proporciones son las mismas que una fotografía de 5 pulgadas por 8 pulgadas.

Solución

$\ \frac{\text { width }}{\text { length }}$	Determinar la relación.
Foto original: $\ \frac{5 \text { inches wide }}{8 \text { inches long }}$ Foto ampliada: $\ \frac{10 \text { inches wide }}{n \text { inches long }}$	Escribe una relación que compare el largo con el ancho de cada fotografía. Usa una letra para representar la cantidad que no se conoce (el ancho de la foto ampliada).
$\ \frac{5}{8}=\frac{10}{n}$	Escribe una proporción que establezca que las dos proporciones son iguales.
$\ 5 \cdot n=8 \cdot 10$	Multiplicar cruz.
$\ 5 n=80$	Estás buscando un número que, cuando se multiplica por 5, te dé 80.
\ (\\ begin {array} {l} \ frac {5 n} {5} =\ frac {80} {5}\ n=\ frac {80} {5} \ end {array}\)	Divide ambos lados por 5 para aislar la variable.
$\ n=16$	\ (\\ begin {array} {r} 16\\\\ 5\ longdiv {80} \ end {array}\)

La longitud de la fotografía ampliada es de 16 pulgadas.

Resolver problemas de aplicación usando proporciones

Establecer y resolver una proporción es una estrategia útil para resolver una variedad de problemas de razonamiento proporcional. En estos problemas, siempre es importante determinar cuál es el valor desconocido, para luego identificar una relación proporcional que pueda usar para resolver para el valor desconocido. A continuación se presentan algunos ejemplos.

Ejemplo

Entre una especie de aves tropicales, 30 de cada 50 aves son hembras. Si cierto santuario de aves tiene una población de 1,150 de estas aves, ¿cuántas de ellas esperarías que fueran hembras?

Solución

Let$\ x$ =el número de aves hembras en el santuario.	Determinar el ítem desconocido: el número de aves hembras en el santuario. Asigna una letra a esta cantidad desconocida.
$\ \frac{30 \text { female birds }}{50 \text { birds }}=\frac{x \text { female birds in sanctuary }}{1,150 \text { birds in sanctuary }}$	Establecer una proporción, estableciendo las proporciones iguales.
$\ \frac{30 \div 10}{50 \div 10}=\frac{3}{5}$ $\ \frac{3}{5}=\frac{x}{1150}$	Simplifica la relación de la izquierda para facilitar la próxima multiplicación cruzada.
\ (\\ comenzar {alineado} 3\ cdot 1150 &=5\ cdot x\\ 3.450 &=5 x \ end {alineado}\)	Multiplicar cruz.
\ (\\ begin {array} {r} 690\\\ 5\ longdiv {3.450} \ end {array}\)	¿Qué número, cuando se multiplica por 5, da un producto de 3,450? Puedes encontrar este valor dividiendo 3,450 por 5.
$\ x=690$aves

Se esperaría que 690 aves en el santuario fueran hembras.

Ejemplo

A Sandra le toma 1 hora procesar palabras 4 páginas. A este ritmo, ¿cuánto tardará en completar 27 páginas?

Solución

$\ \frac{4 \text { pages }}{1 \text { hour }}=\frac{27 \text { pages }}{x \text { hours }}$	Configura una proporción comparando las páginas que escribe y el tiempo que lleva escribirlas.
$\ 4 \cdot x=1 \cdot 27$	Multiplicar cruz.
$\ 4 x=27$	Estás buscando un número que, cuando se multiplica por 4, te dé 27.
\ (\\ begin {array} {r} 6.75\\\ 4\ longdiv {27.00} \ end {array}\)	Puedes encontrar este valor dividiendo 27 por 4.
$\ x=6.75 \text { hours }$

Sandra tardará 6.75 horas en completar 27 páginas.

Ejercicio

Un mapa utiliza una escala donde 2 pulgadas representa 5 millas. Si la distancia entre dos ciudades se muestra en un mapa como 20 pulgadas, ¿a cuántas millas de distancia están las dos ciudades?

50 pulgadas
50 millas
8 millas
100 millas

Contestar

Incorrecto. La distancia entre las ciudades se mide en pulgadas en el mapa, pero en millas en la actualidad. La respuesta correcta es de 50 millas.
Correcto. Estableciendo la proporción$\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$, encuentras esas$\ x=50$ millas.
Incorrecto. Cuando resuelves una proporción, cruzas multiplicas:$\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$,$\ 2 x=5 \cdot 20$. La respuesta correcta es de 50 millas.
Incorrecto. Cuando resuelves una proporción, cruzas multiplicas:$\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$,$\ 2 x=5 \cdot 20$. La respuesta correcta es de 50 millas.

Resumen

Una proporción es una ecuación que compara dos proporciones. Si las proporciones son equivalentes, la proporción es verdadera. Si no, la proporción es falsa. Encontrar un producto cruzado es otro método para determinar si una proporción es verdadera o falsa. La multiplicación cruzada también es útil para encontrar una cantidad desconocida en una relación proporcional. Establecer y resolver proporciones es una habilidad que es útil para resolver una variedad de problemas.

\(\ \frac{\text { printers }}{\text { computers }}=\frac{\text { printers }}{\text { computers }}\)	Identificar la relación.
\(\ \frac{3 \text { printers }}{18 \text { computers }}=\frac{20 \text { printers }}{105 \text { computers }}\)	Escribe proporciones que describan cada situación, y ponerlas iguales entre sí.
Impresoras (check)	Verifique que las unidades en los numeradores coincidan.
Computadoras (check)	Verifique que las unidades en los denominadores coincidan. Simplifica cada fracción y determina si son equivalentes.
\ (\\ begin {array} {c} \ frac {3\ div 3} {18\ div 3} =\ frac {1} {6}\ \ frac {20\ div 5} {105\ div 5} =\ frac {4} {21}\ \ frac {1} {6}\ neq\ frac {4} {21} \ end {array}\)	Dado que las fracciones simplificadas no son iguales (designadas por el\(\ \neq\) signo), la proporción no es cierta.

\(\ 20 \cdot n=4 \cdot 25\)	Multiplicar cruz.
\(\ 20 n=100\)	Estás buscando un número que al multiplicarlo por 20 obtienes 100.
\ (\\ begin {array} {r} 5\\\\ 20\ longdiv {100} \ end {array}\)	Puedes encontrar este valor dividiendo 100 por 20.

\(\ \frac{\text { width }}{\text { length }}\)	Determinar la relación.
Foto original: \(\ \frac{5 \text { inches wide }}{8 \text { inches long }}\) Foto ampliada: \(\ \frac{10 \text { inches wide }}{n \text { inches long }}\)	Escribe una relación que compare el largo con el ancho de cada fotografía. Usa una letra para representar la cantidad que no se conoce (el ancho de la foto ampliada).
\(\ \frac{5}{8}=\frac{10}{n}\)	Escribe una proporción que establezca que las dos proporciones son iguales.
\(\ 5 \cdot n=8 \cdot 10\)	Multiplicar cruz.
\(\ 5 n=80\)	Estás buscando un número que, cuando se multiplica por 5, te dé 80.
\ (\\ begin {array} {l} \ frac {5 n} {5} =\ frac {80} {5}\ n=\ frac {80} {5} \ end {array}\)	Divide ambos lados por 5 para aislar la variable.
\(\ n=16\)	\ (\\ begin {array} {r} 16\\\\ 5\ longdiv {80} \ end {array}\)

Let\(\ x\) =el número de aves hembras en el santuario.	Determinar el ítem desconocido: el número de aves hembras en el santuario. Asigna una letra a esta cantidad desconocida.
\(\ \frac{30 \text { female birds }}{50 \text { birds }}=\frac{x \text { female birds in sanctuary }}{1,150 \text { birds in sanctuary }}\)	Establecer una proporción, estableciendo las proporciones iguales.
\(\ \frac{30 \div 10}{50 \div 10}=\frac{3}{5}\) \(\ \frac{3}{5}=\frac{x}{1150}\)	Simplifica la relación de la izquierda para facilitar la próxima multiplicación cruzada.
\ (\\ comenzar {alineado} 3\ cdot 1150 &=5\ cdot x\\ 3.450 &=5 x \ end {alineado}\)	Multiplicar cruz.
\ (\\ begin {array} {r} 690\\\ 5\ longdiv {3.450} \ end {array}\)	¿Qué número, cuando se multiplica por 5, da un producto de 3,450? Puedes encontrar este valor dividiendo 3,450 por 5.
\(\ x=690\)aves

\(\ \frac{4 \text { pages }}{1 \text { hour }}=\frac{27 \text { pages }}{x \text { hours }}\)	Configura una proporción comparando las páginas que escribe y el tiempo que lleva escribirlas.
\(\ 4 \cdot x=1 \cdot 27\)	Multiplicar cruz.
\(\ 4 x=27\)	Estás buscando un número que, cuando se multiplica por 4, te dé 27.
\ (\\ begin {array} {r} 6.75\\\ 4\ longdiv {27.00} \ end {array}\)	Puedes encontrar este valor dividiendo 27 por 4.
\(\ x=6.75 \text { hours }\)