5.1.1: Convertir porcentajes, decimales y fracciones

Objetivos de aprendizaje

• Describir el significado de porcentaje.
• Representar un número como decimal, porcentaje y fracción.

Introducción

Tres formatos comunes para los números son fracciones, decimales y porcentajes. Los porcentajes se utilizan a menudo para comunicar una cantidad relativa. Probablemente los hayas visto usados para descuentos, donde el porcentaje de descuento puede aplicarse a diferentes precios. Los porcentajes también se utilizan cuando se habla de impuestos y tasas de interés sobre ahorros y préstamos.

El significado del porcentaje

Un porcentaje es una relación de un número a 100. Por ciento significa “por 100”, o “cuántos de cada 100”. Utiliza el símbolo% después de un número para indicar por ciento.

Observe que 12 de los 100 cuadrados en la cuadrícula de abajo han sido sombreados en verde. Esto representa 12 por ciento (12 por 100).

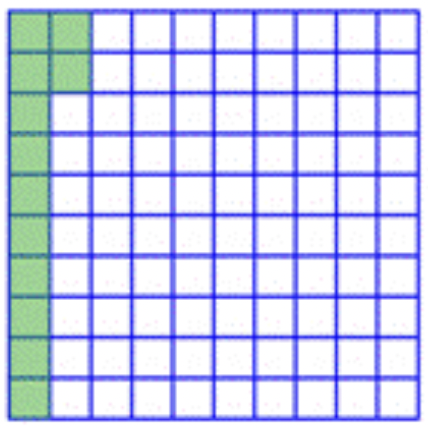\(\ 12 \%=12 \text { percent }=12 \text { parts out of } 100=\frac{12}{100}\)

¿Cuántos de los cuadrados de la cuadrícula anterior no están sombreados? Dado que 12 están sombreados y hay un total de 100 cuadrados, 88 están sin sombrear. La porción no sombreada de toda la rejilla es de 88 partes de 100, o 88% de la rejilla. Observe que las porciones sombreadas y no sombreadas juntas forman el 100% de la cuadrícula (100 de 100 cuadrados).

Ejemplo

¿Qué porcentaje de la cuadrícula está sombreada?

Solución

La cuadrícula se divide en 100 cuadrados más pequeños, con 10 cuadrados en cada fila. 23 cuadrados de cada 100 cuadrados están sombreados.

23% de la cuadrícula está sombreada.

Ejemplo

¿Qué porcentaje del cuadrado grande está sombreado?

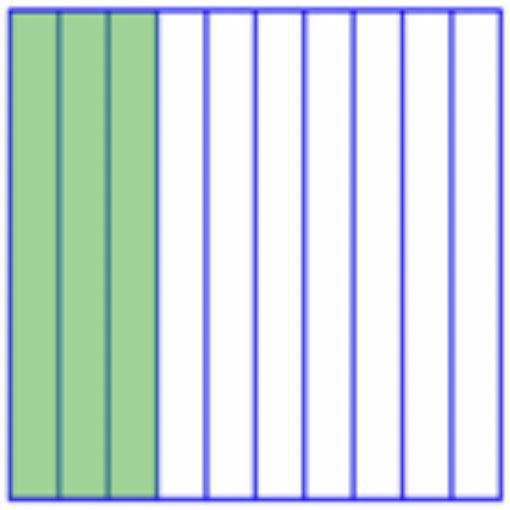
Solución

La cuadrícula se divide en 10 rectángulos. Para porcentajes, es necesario mirar 100 partes de igual tamaño del conjunto. Se puede dividir cada uno de los 10 rectángulos en 10 piezas, dando 100 partes.

30 cuadrados pequeños de cada 100 cuadrados están sombreados.

El 30% del cuadrado grande está sombreado.

Ejercicio

¿Qué porcentaje de esta cuadrícula está sombreada?

1. 3%
2. 11%
3. 38%
4. 62%

Responder

1. Incorrecto. Tres columnas completas de 10 cuadrados están sombreadas, más otros 8 cuadrados de la siguiente columna. Entonces, hay 30+8, o 38, cuadrados sombreados de los 100 cuadrados en la plaza grande. La respuesta correcta es 38%.
2. Incorrecto. Tres columnas completas de 10 cuadrados están sombreadas, más otros 8 cuadrados de la siguiente columna. Entonces, hay 30+8, o 38, cuadrados sombreados de los 100 cuadrados en la plaza grande. La respuesta correcta es 38%.
3. Correcto. Tres columnas completas de 10 cuadrados están sombreadas, más otros 8 cuadrados de la siguiente columna. Entonces, hay 30+8, o 38, cuadrados sombreados de los 100 cuadrados en la plaza grande. Esto significa que el 38% del cuadrado grande está sombreado.
4. Incorrecto. Hay 62 cuadrados pequeños sin sombra de los 100 que hay en el cuadrado grande, por lo que el porcentaje del cuadrado grande que está sin sombra es del 62%. No obstante, la pregunta planteaba qué porcentaje está sombreado. Hay 38 cuadrados sombreados de los 100 cuadrados en el cuadrado grande, por lo que la respuesta correcta es 38%.

Reescritura de porcentajes, decimales y fracciones

A menudo es útil cambiar el formato de un número. Por ejemplo, puede resultarle más fácil agregar decimales que agregar fracciones. Si puedes escribir las fracciones como decimales, puedes agregarlas como decimales. Entonces puedes reescribir tu suma decimal como una fracción, si es necesario.

Los porcentajes se pueden escribir como fracciones y decimales en muy pocos pasos.

Ejemplo

Escribe el 25% como fracción simplificada y como decimal.

Solución

Escribir como una fracción.	\(\ 25 \%=\frac{25}{100}\)	Dado que% significa “de 100”, 25% significa 25 de cada 100. Se escribe esto como una fracción, usando 100 como denominador.
	\(\ \frac{25}{100}=\frac{25 \div 25}{100 \div 25}=\frac{1}{4}\)	Simplifica la fracción dividiendo el numerador y el denominador por el factor común 25.
Escribir como decimal.	\(\ 25 \%=\frac{25}{100}=0.25\)	También puedes simplemente mover el punto decimal en el número entero 25 dos lugares a la izquierda para obtener 0.25.

\(\ 25 \%=\frac{1}{4}=0.25\)

Observe en el diagrama de abajo que el 25% de una cuadrícula también es\(\ \frac{1}{4}\) de la cuadrícula, como encontró en el ejemplo.

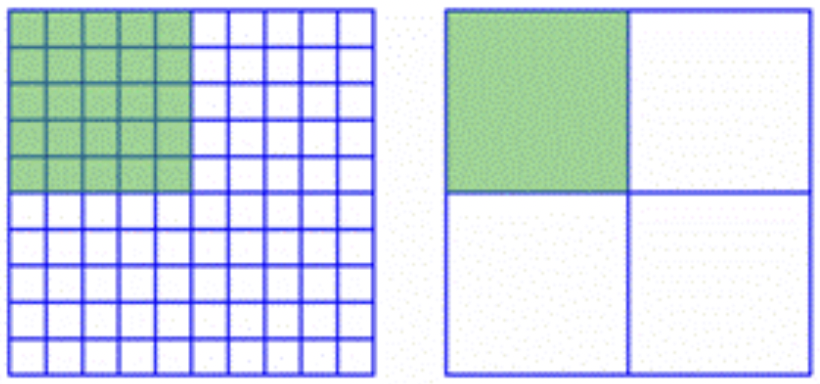
Observe que en el ejemplo anterior, reescribir un porcentaje como decimal toma solo un desplazamiento del punto decimal. Puedes usar fracciones para entender por qué es así. Cualquier porcentaje se\(\ x\) puede representar como la fracción\(\ \frac{x}{100}\), y cualquier fracción se\(\ \frac{x}{100}\) puede escribir como decimal moviendo el punto decimal en\(\ x\) dos lugares hacia la izquierda. Por ejemplo, 81% se puede escribir como\(\ \frac{81}{100}\), y dividir 81 por 100 resulta en 0.81. La gente suele saltarse el paso de fracción intermediaria y simplemente convierte un porcentaje a un decimal moviendo el punto decimal dos lugares hacia la izquierda.

De la misma manera, reescribir un decimal como porcentaje (o como fracción) requiere pocos pasos.

Ejemplo

Escribe 0.6 como porcentaje y como fracción simplificada.

Solución

Escribir como porcentaje.	\(\ 0.6=0.60=60 \%\)	Escribe 0.6 como 0.60, que es 60 centésimas. 60 centésimas es 60 por ciento. También puede mover el punto decimal dos lugares a la derecha para encontrar el porcentaje equivalente.
Escribir como una fracción.	\(\ 0.6=\frac{6}{10}\)	Para escribir 0.6 como fracción, se lee el decimal, 6 décimas, y escribe 6 décimas en forma de fracción.
	\(\ \frac{6}{10}=\frac{6 \div 2}{10 \div 2}=\frac{3}{5}\)	Simplifica la fracción dividiendo el numerador y el denominador por 2, un factor común.

\(\ 0.6=60 \%=\frac{3}{5}\)

En este ejemplo, el porcentaje no es un número entero. Puedes manejar esto de la misma manera, pero suele ser más fácil convertir el porcentaje a un decimal y luego convertir el decimal a una fracción.

Ejemplo

Escribe 5.6% como decimal y como fracción simplificada.

Solución

Escribir como decimal.	\(\ 5.6 \%=0.056\)	Mueve el punto decimal dos lugares hacia la izquierda. En este caso, inserte un 0 delante del 5 (05.6) para poder mover el decimal a la izquierda dos lugares.
Escribir como una fracción.	\(\ 0.056=\frac{56}{1,000}\)	Escribe la fracción como leerías el decimal. El último dígito está en el lugar de las milésimas, por lo que el denominador es 1,000.
	\(\ \frac{56}{1,000}=\frac{56 \div 8}{1,000 \div 8}=\frac{7}{125}\)	Simplifica la fracción dividiendo el numerador y el denominador entre 8, un factor común.

\(\ 5.6 \%=\frac{7}{125}=0.056\)

Ejercicio

Escribe 0.645 como porcentaje y como fracción simplificada.

1. 64.5% y\(\ \frac{129}{200}\)
2. 0.645% y\(\ \frac{645}{1,000}\)
3. 645% y\(\ \frac{645}{1}\)
4. 64.5% y\(\ \frac{200}{129}\)

Responder

1. Correcto. \(\ 0.645=64.5 \%=\frac{129}{200}\)
2. Incorrecto. \(\ 0.645=64.5 \%\), no\(\ 0.645 \%\). Recuerda que cuando conviertes un decimal a un porcentaje, tienes que mover el punto decimal dos lugares a la derecha. La respuesta correcta es\(\ 64.5 \%\) y\(\ \frac{129}{200}\).
3. Incorrecto. \(\ 0.645=64.5 \%\), no\(\ 645 \%\). Recuerda que cuando conviertes un decimal a un porcentaje, tienes que mover el punto decimal dos lugares a la derecha. La respuesta correcta es\(\ 64.5 \%\) y\(\ \frac{129}{200}\).
4. Incorrecto. Para escribir 0.645 como porcentaje, mueva el punto decimal dos lugares a la derecha:\(\ 64.5 \%\). Para escribir 0.645 como fracción, usa 645 como numerador. El valor posicional del último dígito (el 5) es milésimas, por lo que el denominador es 1,000. La fracción es\(\ \frac{645}{1,000}\). El mayor factor común de 645 y 1,000 es 5, por lo que puedes dividir el numerador y denominador por 5 para obtener\(\ \frac{129}{200}\). La respuesta correcta es\(\ 64.5 \%\) y\(\ \frac{129}{200}\).

Para escribir una fracción como decimal o por ciento, se puede escribir la fracción como una fracción equivalente con un denominador de 10 (o cualquier otra potencia de 10 como 100 o 1,000), que luego se puede convertir a un decimal y luego a un porcentaje.

Ejemplo

Escribir\(\ \frac{3}{4}\) como decimal y como porcentaje.

Solución

Escribir como decimal.	\(\ \frac{3}{4}=\frac{3 \cdot 25}{4 \cdot 25}=\frac{75}{100}\)	Encuentra una fracción equivalente con 10, 100, 1,000, u otra potencia de 10 en el denominador. Dado que 100 es un múltiplo de 4, puedes multiplicar 4 por 25 para obtener 100. Multiplica tanto el numerador como el denominador por 25.
	\(\ \frac{75}{100}=0.75\)	Escribe la fracción como decimal con el 5 en el lugar centésimas.
Escribir como porcentaje.	\(\ 0.75=75 \%\)	Para escribir el decimal como porcentaje, mueva el punto decimal dos lugares hacia la derecha.

\(\ \frac{3}{4}=0.75=75 \%\)

Si es difícil encontrar una fracción equivalente con un denominador de 10, 100, 1,000, y así sucesivamente, siempre se puede dividir el numerador por el denominador para encontrar el equivalente decimal.

Ejemplo

Escribir\(\ \frac{3}{8}\) como decimal y como porcentaje.

Solución

Escribir como decimal.	\(\ \frac{3}{8}=3 \div 8\) \ (\\ begin {array} {r} 0.375\\\ 8\ longdiv {3.000} \ end {array}\)	Divide el numerador por el denominador. \(\ 3 \div 8=0.375\)
Escribir como porcentaje.	\(\ 0.375=37.5 \%\)	Para escribir el decimal como porcentaje, mueva el punto decimal dos lugares hacia la derecha.

\(\ \frac{3}{8}=0.375=37.5 \%\)

Ejercicio

Escribir\(\ \frac{4}{5}\) como decimal y como porcentaje.

1. \(\ 80.0 \text { and } 0.8 \%\)
2. \(\ 0.4 \text { and } 4 \%\)
3. \(\ 0.8 \text { and } 80 \%\)
4. \(\ 0.8 \text { and } 8 \%\)

Responder

1. Incorrecto. Observe que 10 es múltiplo de 5, por lo que puede reescribir\(\ \frac{4}{5}\) usando 10 como denominador. Multiplica el numerador y denominador por 2 para obtener\(\ \frac{8}{10}\). El decimal equivalente es 0.8. Se puede escribir esto como un porcentaje moviendo el punto decimal dos lugares hacia la derecha. Ya que 0.8 tiene un solo lugar a la derecha, incluir 0 en el lugar centésimas:\(\ 0.8=0.80=80 \%\). La respuesta correcta es 0.8 y 80%.
2. Incorrecto. Para encontrar un equivalente decimal para\(\ \frac{4}{5}\), primero convierta la fracción a décimas. Multiplica el numerador y denominador por 2 para obtener\(\ \frac{8}{10}\). El decimal equivalente es 0.8 So,\(\ \frac{4}{5}\) y 0.4 no son cantidades equivalentes. La respuesta correcta es 0.8 y 80%.
3. Correcto. La respuesta es\(\ \frac{4}{5}=0.8=80 \%\).
4. Incorrecto. Es cierto que\(\ \frac{4}{5}=0.8\), pero esto no equivale al 8%. Para escribir 0.8 como porcentaje, mueva el punto decimal dos lugares a la derecha:\(\ 0.8=0.80=80 \%\). La respuesta correcta es 0.8 y 80%.

Números Mixtos

Todos los ejemplos anteriores involucran fracciones y decimales menores a 1, por lo que todos los porcentajes que has visto hasta ahora han sido inferiores al 100%.

También son posibles porcentajes mayores al 100%. Se utilizan porcentajes superiores al 100% para describir situaciones en las que hay más de un entero (fracciones y decimales mayores a 1 se utilizan por la misma razón).

En el siguiente diagrama, el 115% está sombreado. Cada cuadrícula se considera un todo, y se necesitan dos rejillas para 115%.

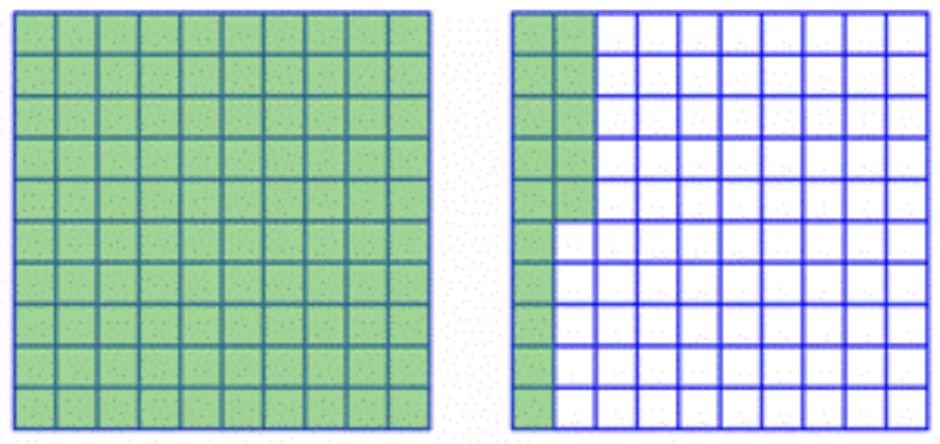
Expresado como decimal, el porcentaje 115% es 1.15; como fracción, es\(\ 1 \frac{15}{100}\), o\(\ 1 \frac{3}{20}\). Observe que aún puede convertir entre porcentajes, fracciones y decimales cuando la cantidad es mayor que un todo.

Los números mayores a uno que incluyen una parte fraccionaria se pueden escribir como la suma de un número entero y la parte fraccionaria. Por ejemplo, el número mixto\(\ 3 \frac{1}{4}\) es la suma del número entero 3 y la fracción\(\ \frac{1}{4} \cdot 3 \frac{1}{4}=3+\frac{1}{4}\).

Ejemplo

Escribir\(\ 2 \frac{7}{8}\) como decimal y como porcentaje.

Solución

Escribir como decimal.	\(\ 2 \frac{7}{8}=2+\frac{7}{8}\)	Escribe la fracción mixta como 2 enteros más la parte fraccionaria.
	\(\ \frac{7}{8}=7 \div 8\) \ (\\ begin {array} {r} 0.875\\\ 8\ longdiv {7.000} \ end {array}\)	Escribe la parte fraccionaria como decimal dividiendo el numerador por el denominador\(\ 7 \div 8=0.875\).
	\(\ 2+0.875=2.875\)	Agrega 2 al decimal.
Escribir como porcentaje.	\(\ 2.875=287.5 \%\)	Ahora puedes mover el punto decimal dos lugares a la derecha para escribir el decimal como porcentaje.

\(\ 2 \frac{7}{8}=2.875=287.5 \%\)

Tenga en cuenta que un número entero puede escribirse como un porcentaje. 100% significa un todo; entonces dos enteros serían 200%.

Ejemplo

Escribe 375% como decimal y como fracción simplificada.

Solución

Escribir como decimal.	\(\ 375 \%=3.75\)	Mueve el punto decimal dos lugares hacia la izquierda. Tenga en cuenta que hay un número entero junto con el decimal ya que el porcentaje es superior al 100%.
Escribir como una fracción.	\(\ 3.75=3+0.75\)	Escribe el decimal como una suma del número entero y la parte fraccionaria.
	\(\ 0.75=\frac{75}{100}\)	Escribe la parte decimal como fracción.
	\(\ \frac{75}{100}=\frac{75 \div 25}{100 \div 25}=\frac{3}{4}\)	Simplifica la fracción dividiendo el numerador y el denominador por un factor común de 25.
	\(\ 3+\frac{3}{4}=3 \frac{3}{4}\)	Suma la parte del número entero a la fracción.

\(\ 375 \%=3.75=3 \frac{3}{4}\)

Ejercicio

Escribir 4.12 como porcentaje y como fracción simplificada.

1. \(\ 0.0412 \% \text { and } \frac{412}{100}\)
2. \(\ 412 \% \text { and } 4 \frac{3}{25}\)
3. \(\ 412 \% \text { and } \frac{103}{250}\)
4. \(\ 4.12 \% \text { and } 4 \frac{3}{25}\)

Responder

1. Incorrecto. Para convertir 4.12 a un porcentaje, mueva el punto decimal dos lugares a la derecha, no a la izquierda. La respuesta correcta es 412% y\(\ 4 \frac{3}{25}\).
2. Correcto. 4.12 equivale a 412%, y la forma simplificada de\(\ 4 \frac{12}{100}\) es\(\ 4 \frac{3}{25}\).
3. Incorrecto. 4.12 hace igual 412%, pero también es equivalente a\(\ 4 \frac{12}{100}\), no\(\ \frac{412}{1,000}\). La respuesta correcta es 412% y\(\ 4 \frac{3}{25}\).
4. Incorrecto. Para convertir 4.12 a un porcentaje, mueva el punto decimal dos lugares hacia la derecha. La respuesta correcta es 412% y\(\ 4 \frac{3}{25}\).

Resumen

Los porcentajes son una forma común de representar cantidades fraccionarias, tal como lo son los decimales y las fracciones. Cualquier número que pueda escribirse como decimal, fracción o porcentaje también se puede escribir usando las otras dos representaciones.