6.3.1: Básculas de Temperatura

Objetivos de aprendizaje

• Anote los puntos de congelación y ebullición del agua en las escalas de temperatura Celsius y Fahrenheit.
• Convierta de una escala de temperatura a otra, usando fórmulas de conversión.

Introducción

Enciende la televisión cualquier mañana y verás meteorólogos hablando del pronóstico del tiempo del día. Además de decirte cómo serán las condiciones climáticas (soleado, nublado, lluvioso, bochornoso), también te dicen el pronóstico del día para temperaturas altas y bajas. Un caluroso día de verano puede llegar a los 100 ^o en Filadelfia, mientras que un día fresco de primavera puede tener un mínimo de 40 ^o en Seattle.

Sin embargo, si has estado en otros países, puedes notar que los meteorólogos miden el calor y el frío de manera diferente fuera de Estados Unidos. Por ejemplo, un meteorólogo de televisión en San Diego puede pronosticar un máximo de 89 ^o, pero un pronosticador similar en Tijuana, México, que está a solo 20 millas al sur, puede mirar el mismo patrón meteorológico y decir que la temperatura alta del día va a ser de 32 ^o. ¿Qué está pasando aquí?

La diferencia es que los dos países utilizan diferentes escalas de temperatura. En Estados Unidos, las temperaturas suelen medirse utilizando la escala Fahrenheit, mientras que la mayoría de los países que utilizan el sistema métrico utilizan la escala Celsius para registrar temperaturas. Aprender sobre las diferentes escalas, incluyendo cómo convertir entre ellas, te ayudará a descubrir cómo va a ser el clima, sin importar en qué país te encuentres.

Medición de la temperatura en dos escalas

Fahrenheit y Celsius son dos escalas diferentes para medir la temperatura.

Aquí se muestra un termómetro que mide una temperatura de 22 ^o Celsius.		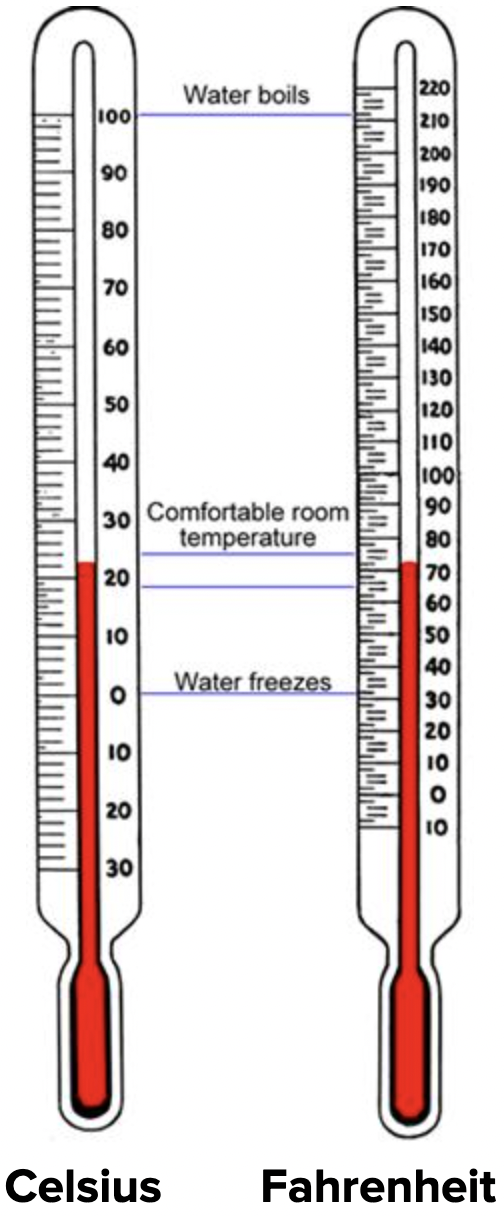Un termómetro que mide una temperatura de 72 ^o Fahrenheit que se muestra aquí.
En la escala Celsius, el agua se congela a 0 ^o y hierve a 100 ^o.		En la escala Fahrenheit, el agua se congela a 32 ^o y hierve a 212 ^o.
Si Estados Unidos adoptara la escala Celsius, las temperaturas pronosticadas rara vez irían por debajo de -30 ^o o por encima de 45 ^o. (Se puede pronosticar una temperatura de -18 ^o para un día frío de invierno en Michigan, mientras que se puede predecir una temperatura de 43 ^o para un caluroso día de verano en Arizona.)		En Estados Unidos, las temperaturas pronosticadas medidas en Fahrenheit rara vez van por debajo de -20 ^o o por encima de 120 ^o. (Se puede pronosticar una temperatura de 0 ^o para un día frío de invierno en Michigan, mientras que se puede predecir una temperatura de 110 ^o para un caluroso día de verano en Arizona.)
La mayoría de los edificios de oficinas mantienen una temperatura interior entre 18 ^o Celsius y 24 ^o Celsius para mantener cómodos a los empleados.		La mayoría de los edificios de oficinas mantienen una temperatura interior entre 65 ^o Fahrenheit y 75 ^o Fahrenheit para mantener cómodos a los empleados.

Ejercicio

Un cocinero pone un termómetro en una olla de agua para ver qué tan caliente está. El termómetro lee 132 ^o, pero el agua aún no está hirviendo. ¿Qué escala de temperatura mide el termómetro?

1. Celsius
2. Fahrenheit

Contestar

1. Incorrecto. En la escala Celsius, el agua hierve a 100 ^o, por lo que si el agua no está hirviendo y la medición es superior a 100 ^o, entonces no puede ser Celsius. La respuesta correcta es Fahrenheit.
2. Correcto. El agua hierve a 212 ^o en la escala Fahrenheit, por lo que una medición de 132 ^o en una escala de Fahrenheit es legítima para el agua caliente (pero no hirviendo).

Conversión entre las escalas

Al mirar los dos termómetros que se muestran, se pueden hacer algunas comparaciones generales entre las escalas. Por ejemplo, muchas personas tienden a sentirse cómodas en temperaturas exteriores entre 50 ^o Fahrenheit y 80 ^o Fahrenheit (o entre 10 ^o Celsius y 25 ^o Celsius). Si un meteorólogo predice una temperatura promedio de 0 ^o Celsius (^{o 32 o} Fahrenheit), entonces es una apuesta segura que necesitarás una chaqueta de invierno.

En ocasiones, es necesario convertir una medida Celsius a su medida exacta de Fahrenheit o viceversa. Por ejemplo, ¿y si quieres conocer la temperatura de tu hijo en Fahrenheit, y el único termómetro que tienes mide la temperatura en medida Celsius? Convertir la temperatura entre los sistemas es un proceso sencillo siempre y cuando utilice las fórmulas que se proporcionan a continuación.

Formulas de conversión de temperatura

Para convertir una medida de Fahrenheit en una medida Celsius, use esta fórmula.

\(\ C=\frac{5}{9}(F-32)\)

Para convertir una medida Celsius en una medición de Fahrenheit, use esta fórmula.

\(\ F=\frac{9}{5} C+32\)

¿Cómo se desarrollaron estas fórmulas? Vinieron de comparar las dos escalas. Dado que el punto de congelación es 0 ^o en la escala Celsius y 32 ^o en la escala Fahrenheit, restamos 32 al convertir de Fahrenheit a Celsius, y sumamos 32 al convertir de Celsius a Fahrenheit.

También hay una razón para las fracciones\(\ \frac{5}{9}\) y\(\ \frac{9}{5}\). Hay 100 grados entre los puntos de congelación (0 ^o) y ebullición (100 ^o) del agua en la escala Celsius y 180 grados entre los puntos similares (32 ^o y 212 ^o) en la escala Fahrenheit. Escribiendo estas dos escalas como una relación,\(\ \frac{F^{\circ}}{C^{\circ}}\), da\(\ \frac{180^{\circ}}{100^{\circ}}=\frac{180^{\circ} \div 20}{100^{\circ} \div 20}=\frac{9}{5}\). Si volteas la proporción para ser\(\ \frac{C^{\circ}}{F^{\circ}}\), obtienes\(\ \frac{100^{\circ}}{180^{\circ}}=\frac{100^{\circ} \div 20}{180^{\circ} \div 20}=\frac{5}{9}\). Observe cómo se utilizan estas fracciones en las fórmulas de conversión.

El siguiente ejemplo ilustra la conversión de la temperatura Celsius a temperatura Fahrenheit, utilizando el punto de ebullición del agua, que es de 100 ^o Celsius.

Ejemplo

El punto de ebullición del agua es de 100 ^o Celsius. ¿A qué temperatura hierve el agua en la escala Fahrenheit?

Solución

\(\ F=\frac{9}{5} C+32\)	Se da una temperatura Celsius. Para convertirlo a la escala Fahrenheit, usa la fórmula de la izquierda.
\(\ F=\frac{9}{5}(100)+32\) \(\ F=\frac{900}{5}+32\)	Sustituye 100\(\ C\) y multiplica.
\(\ F=\frac{900 \div 5}{5 \div 5}+32\) \(\ F=\frac{180}{1}+32\)	Simplifica\(\ \frac{900}{5}\) dividiendo el numerador y el denominador por 5.
\(\ F=212\)	Agregar 180+32

El punto de ebullición del agua es de 212 ^o Fahrenheit.

Ejemplo

El agua se congela a 32 ^o Fahrenheit. En la escala Celsius, ¿qué temperatura es esta?

Solución

\(\ C=\frac{5}{9}(F-32)\)	Se da una temperatura de Fahrenheit. Para convertirlo a la escala Celsius, usa la fórmula de la izquierda.
\(\ C=\frac{5}{9}(32-32)\)	Sustituir 32\(\ F\) y restar.
\(\ C=\frac{5}{9}(0)\)	Cualquier número multiplicado por 0 es 0.
\(\ C=0\)

El punto de congelación del agua es de 0 ^o Celsius.

Los dos problemas anteriores utilizaron las fórmulas de conversión para verificar algunas conversiones de temperatura que se discutieron anteriormente: los puntos de ebullición y congelación del agua. El siguiente ejemplo muestra cómo se pueden usar estas fórmulas para resolver un problema del mundo real usando diferentes escalas de temperatura.

Ejemplo

Dos científicos están haciendo un experimento diseñado para identificar el punto de ebullición de un líquido desconocido. Un científico obtiene un resultado de 120 ^o Celsius; el otro obtiene un resultado de 250 ^o Fahrenheit. ¿Qué temperatura es más alta y por cuánto?

Solución

¿Cuál es la diferencia entre 120 ^o Celsius y 250 ^o Fahrenheit?	Una temperatura se da en grados Celsius, y la otra se da en grados Fahrenheit. Para encontrar la diferencia entre ellos, necesitamos medirlos en la misma escala.
\(\ F=\frac{9}{5} C+32\)	Usa la fórmula de conversión para convertir 120 ^o Celsius a grados Fahrenheit. (En su lugar podrías convertir 250 ^o Fahrenheit a grados Celsius; esto se explica en el texto que sigue a este ejemplo).
\(\ F=\frac{9}{5}(120)+32\)	Sustituto 120 para\(\ C\).
\(\ F=\frac{1080}{5}+32\)	Multiplicar.
\(\ F=\frac{1080 \div 5}{5 \div 5}+32\)	Simplifica\(\ \frac{1080}{5}\) dividiendo el numerador y el denominador por 5.
\(\ F=\frac{216}{1}+32\)	Agregar\(\ 216+32\).
\(\ F=248\)	Eso lo has encontrado\(\ 120^{\circ} \mathrm{C}=248^{\circ} \mathrm{F}\).
\(\ 250^{\circ}-248^{\circ}=2^{\circ} \text { Fahrenheit }\)	Para encontrar la diferencia entre 248 ^o Fahrenheit y 250 ^o Fahrenheit, restar.

250 ^o Fahrenheit es la temperatura más alta en 2 ^o Fahrenheit.

Podrías haber convertido 250 ^o Fahrenheit a grados Celsius en su lugar, y luego encontrar la diferencia en las dos medidas. (Si lo hubieras hecho de esta manera, habrías encontrado que 250 ^o F=121.1 ^o C, y que 121.1 ^o Celsius es 1.1 ^o Celsius superior a 120 ^o Celsius.) Sea cual sea la forma que elija, es importante comparar las mediciones de temperatura dentro de la misma escala y aplicar las fórmulas de conversión con precisión.

Ejercicio

Tatiana está investigando destinos vacacionales, y ve que la temperatura media del verano en Barcelona, España es de alrededor de los 26 ^o centígrados. ¿Cuál es la temperatura promedio en grados Fahrenheit?

1. \(\ 79^{\circ} \text { Fahrenheit }\)
2. \(\ -3^{\circ} \text { Fahrenheit }\)
3. \(\ 45^{\circ} \text { Fahrenheit }\)
4. \(\ 58^{\circ} \text { Fahrenheit }\)

Contestar

1. Correcto. Tatiana puede encontrar el equivalente Fahrenheit resolviendo la ecuación\(\ F=\frac{9}{5}(26)+32\). El resultado es 78.8 ^o Fahrenheit, que redondea a 79 ^o Fahrenheit.
2. Incorrecto. Usaste la fórmula equivocada. Para encontrar el equivalente Fahrenheit, usa la fórmula\(\ F=\frac{9}{5} C+32\). La respuesta correcta es 79 ^o Fahrenheit.
3. Incorrecto. Usted aplicó mal la fórmula; intente sustituir 26 por\(\ C\) en la fórmula\(\ F=\frac{9}{5} C+32\). La respuesta correcta es 79 ^o Fahrenheit.
4. Incorrecto. Usted aplicó mal la fórmula; intente sustituir 26 por\(\ C\) en la fórmula\(\ F=\frac{9}{5} C+32\). La respuesta correcta es 79 ^o Fahrenheit.

Resumen

La temperatura a menudo se mide en una de dos escalas: la escala Celsius y la escala Fahrenheit. Un termómetro Celsius medirá el punto de ebullición del agua a 100 ^o y su punto de congelación a 0 ^o; un termómetro de Fahrenheit medirá los mismos eventos a 212 ^o para el punto de ebullición del agua y 32 ^o como su punto de congelación. Puede utilizar fórmulas de conversión para convertir una medida realizada en una escala a otra escala.