7.3.1: Sólidos
- Page ID
- 111354
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identificar sólidos geométricos.
- Encuentra el volumen de sólidos geométricos.
- Encuentra el volumen de un sólido geométrico compuesto.
Introducción
Vivir en un mundo bidimensional sería bastante aburrido. Agradecidamente, todos los objetos físicos que ves y usas todos los días, como computadoras, teléfonos, autos y zapatos, existen en tres dimensiones. Todos ellos tienen largo, ancho y alto. (Incluso los objetos muy delgados como una hoja de papel son tridimensionales. El grosor de una hoja de papel puede ser de una fracción de milímetro, pero sí existe).
En el mundo de la geometría, es común ver figuras tridimensionales. En matemáticas, un lado plano de una figura tridimensional se llama cara. Los poliedros son formas que tienen cuatro o más caras, siendo cada una un polígono. Estos incluyen cubos, prismas y pirámides. A veces incluso se pueden ver figuras individuales que son compuestos de dos de estas figuras. Echemos un vistazo a algunos poliedros comunes.
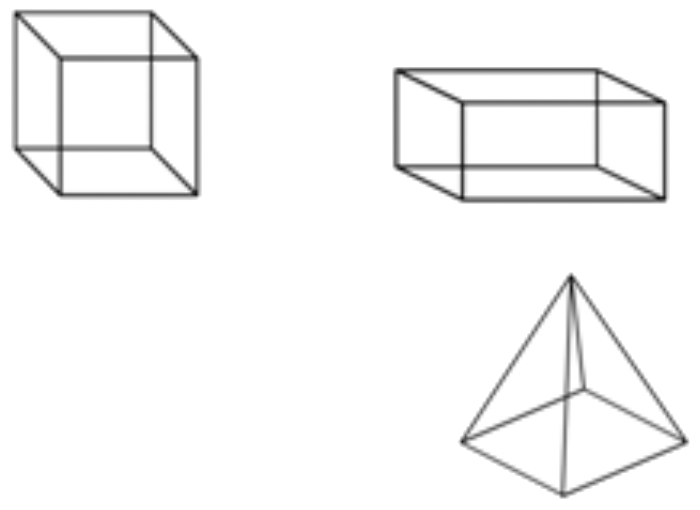
Identificación de Sólidos
El primer conjunto de sólidos contiene bases rectangulares. Echa un vistazo a la tabla a continuación, que muestra cada figura tanto en forma sólida como transparente.
| Nombre | Definición | Forma Sólida | Forma Transparente |
| Cube | Un poliedro de seis lados que tiene cuadrados congruentes como caras. |  |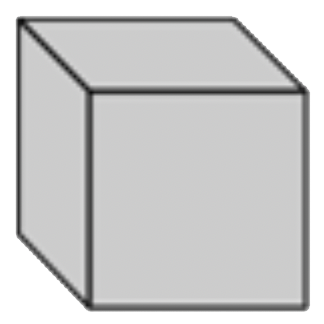
 |
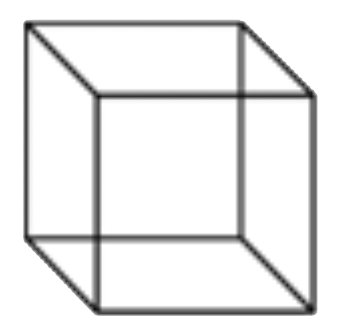| Prisma rectangular | Un poliedro que tiene tres pares de caras congruentes, rectangulares y paralelas. |  |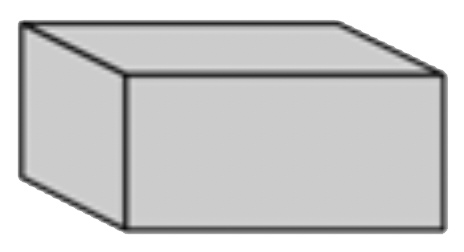
 |
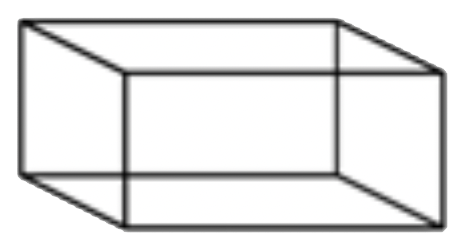| Pyramid | Un poliedro con una base poligonal y una colección de caras triangulares que se encuentran en un punto. |  |
 |
Observe los diferentes nombres que se utilizan para estas figuras. Un cubo es diferente a un cuadrado, aunque a veces se confunden entre sí; un cubo tiene tres dimensiones, mientras que un cuadrado solo tiene dos. Del mismo modo, describirías una caja de zapatos como un prisma rectangular (no simplemente un rectángulo), y las antiguas pirámides de Egipto como... bueno, ¡como pirámides (no triángulos)!
En este siguiente conjunto de sólidos, cada figura tiene una base circular.
| Nombre | Definición | Forma Sólida | Forma Transparente |
| Cilindro | Una figura sólida con un par de bases circulares paralelas y una cara redonda y lisa entre ellas. |  |
 |
 |
 |
Tómate un momento para comparar una pirámide y un cono. Observe que una pirámide tiene una base rectangular y caras planas y triangulares; un cono tiene una base circular y un cuerpo liso y redondeado.
Por último, veamos una forma que es única: una esfera.
| Nombre | Definición | Forma Sólida | Forma Transparente |
| Esfera | Una figura sólida y redonda donde cada punto de la superficie está a la misma distancia del centro. |  |
 |
Hay muchos objetos esféricos a tu alrededor: balones de fútbol, pelotas de tenis y pelotas de beisbol que son tres elementos comunes. Si bien pueden no ser perfectamente esféricas, generalmente se les conoce como esferas.
Una figura tridimensional tiene las siguientes propiedades:
- Tiene una base rectangular.
- Tiene cuatro caras triangulares.
¿Qué clase de sólido es?
Solución
 |
Una base rectangular indica que debe ser un cubo, un prisma rectangular o una pirámide. |
 |
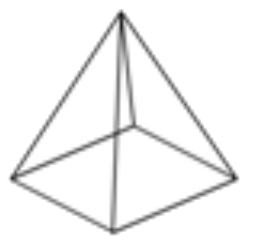Dado que las caras son triangulares, debe ser una pirámide. |
El sólido es una pirámide.
Volumen
Recordemos que el perímetro mide una dimensión (largo), y el área mide dos dimensiones (largo y ancho). Para medir la cantidad de espacio que ocupa una figura tridimensional, se utiliza otra medida llamada volumen.
Para visualizar qué mide el “volumen”, mire hacia atrás a la imagen transparente del prisma rectangular mencionado anteriormente (o simplemente piense en una caja de zapatos vacía). Imagina apilar cubos idénticos dentro de esa caja para que no haya huecos entre ninguno de los cubos. Imagínese llenar toda la caja de esta manera. Si contaras el número de cubos que caben dentro de ese prisma rectangular, tendrías su volumen.
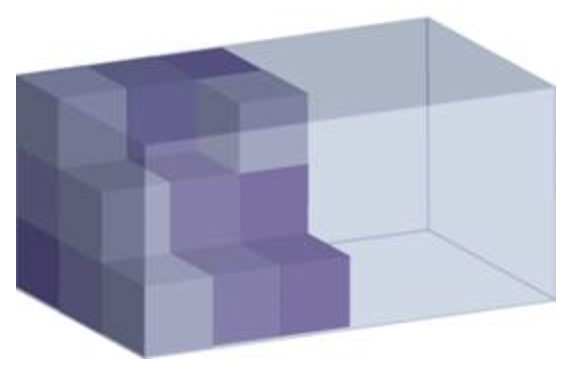
El volumen se mide en unidades cúbicas. La caja de zapatos ilustrada anteriormente puede medirse en pulgadas cúbicas (generalmente representadas como en 3 o pulgadas 3), mientras que la Gran Pirámide de Egipto se mediría más apropiadamente en metros cúbicos (m 3 o metros 3).
Para encontrar el volumen de un sólido geométrico, podrías crear una versión transparente del sólido, crear un montón de cubos 1 por 1 por 1 y luego apilarlos cuidadosamente dentro. Sin embargo, ¡eso llevaría mucho tiempo! Una manera mucho más fácil de encontrar el volumen es familiarizarse con algunas fórmulas geométricas, y usarlas en su lugar.
Repasemos una vez más los sólidos geométricos y enumeremos la fórmula de volumen para cada uno.
Al mirar a través de la lista a continuación, puede notar que algunas de las fórmulas de volumen se parecen a sus fórmulas de área. Para encontrar el volumen de un prisma rectangular, se encuentra el área de la base y luego se multiplica eso por la altura.
| Nombre | Forma Transparente | Fórmula de volumen |
| Cube |  |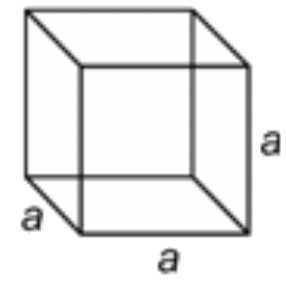
\(\ V=a \cdot a \cdot a=a^{3}\) \(\ a=\text { the length of one side }\) |
| Prisma rectangular |  |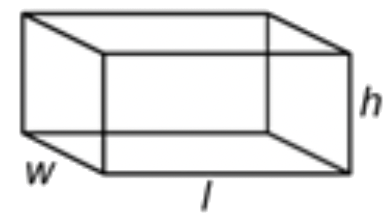
\(\ V=l \cdot w \cdot h\) \ (\\ begin {array} {l} |
 |
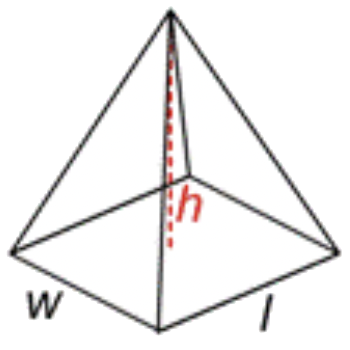\(\ V=\frac{l \cdot w \cdot h}{3}\) \ (\\ begin {array} {l} |
Recuerda que todos los cubos son prismas rectangulares, por lo que la fórmula para encontrar el volumen de un cubo es el área de la base del cubo multiplicada por la altura.
Ahora veamos sólidos que tienen una base circular.
| Nombre | Forma Transparente | Fórmula de volumen |
| Cilindro |  |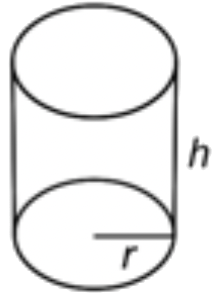
\(\ V=\pi \cdot r^{2} \cdot h\) \ (\\ begin {array} {l} |
| Cono |  |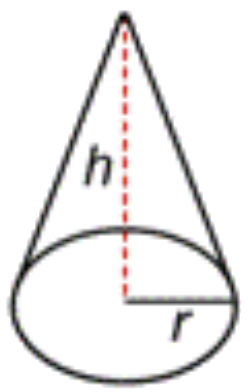
\(\ V=\frac{\pi \cdot r^{2} \cdot h}{3}\) \ (\\ begin {array} {l} |
Aquí\(\ \pi\) vuelve a ver el número.
El volumen de un cilindro es el área de su base,\(\ \pi r^{2}\), multiplicada por su altura,\(\ h\).
Compara la fórmula para el volumen de un cono (\(\ V=\frac{\pi \cdot r^{2} \cdot h}{3}\)) con la fórmula para el volumen de una pirámide (\(\ V=\frac{l \cdot w \cdot h}{3}\)). El numerador de la fórmula de cono es la fórmula de volumen para un cilindro, y el numerador de la fórmula piramidal es la fórmula de volumen para un prisma rectangular. Luego divide cada uno por 3 para encontrar el volumen del cono y la pirámide. Buscar patrones y similitudes en las fórmulas puede ayudarte a recordar qué fórmula se refiere a un sólido dado.
Por último, a continuación se proporciona la fórmula para una esfera. Observe que el radio es cúbico, no cuadrado y que la cantidad\(\ \pi r^{3}\) se multiplica por\(\ \frac{4}{3}\).
| Nombre | Forma de estructura de alambre | Fórmula de volumen |
| Esfera |  |
\(\ V=\frac{4}{3} \pi r^{3}\) \(\ r=\text { radius }\) |
Aplicación de las Fórmulas
Ya sabes identificar los sólidos, y también conoces las fórmulas de volumen para estos sólidos. Para calcular el volumen real de una forma dada, todo lo que necesita hacer es sustituir las dimensiones del sólido en la fórmula y calcular.
En los ejemplos a continuación, observe que se utilizan unidades cúbicas (metros 3, pulgadas 3, pies 3).
Encuentra el volumen de un cubo con longitudes laterales de 6 metros.
Solución
|
\(\ V=a \cdot a \cdot a=a^{3}\) \(\ a=\text { side length }\) |
Identificar la fórmula adecuada a utilizar. |
| \(\ V=6 \cdot 6 \cdot 6=6^{3}\) | Sustituir\(\ a=6\) en la fórmula. |
| \(\ 6 \cdot 6 \cdot 6=216\) | Calcular el volumen. |
\(\ \text { Volume }=216 \text { meters }^{3}\)
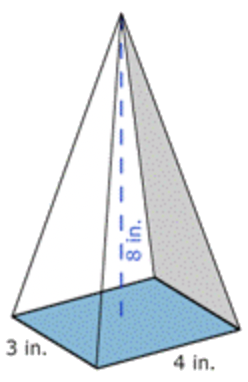
Encuentra el volumen de la forma que se muestra a continuación.
Solución
| Pyramid | Identificar la forma. Tiene una base rectangular y se eleva a un punto, por lo que es una pirámide. |
| \(\ V=\frac{l \cdot w \cdot h}{3}\) | Identificar la fórmula adecuada a utilizar. |
| \ (\\ begin {array} {l} l&=\ texto {longitud}\\ w&=\ texto {ancho}\\ h&=\ texto {altura}\\\ 4&=\ texto {longitud}\\ 3&=\ texto {ancho}\\ 8&=\ texto {altura} \ end {array}\) |
Usa la imagen para identificar las dimensiones. Después sustituya\(\ l=4, w=3, \text{and }h=8\) en la fórmula. |
| \ (\\ begin {array} {c} V=\ frac {4\ cdot 3\ cdot 8} {3}\\ V=\ frac {96} {3}\\ =32 \ end {array}\) |
Calcular el volumen. |
El volumen de la pirámide es\(\ 32 \text { inches }^{3}\).
Encuentra el volumen de la forma que se muestra a continuación.
Usa 3.14 para\(\ \pi\), y redondea la respuesta a la centésima más cercana.
Solución
| Cilindro | Identificar la forma. Tiene una base circular y tiene espesor uniforme (o altura), por lo que es un cilindro. |
| \(\ V=\pi \cdot r^{2} \cdot h\) | Identificar la fórmula adecuada a utilizar. |
| \(\ V=\pi \cdot 7^{2} \cdot 1\) | Usa la imagen para identificar las dimensiones. Después sustituya\(\ r=7\) y\(\ h=1\) en la fórmula. |
| \ (\\ begin {array} {c} V=\ pi\ cdot 49\ cdot 1\\ =49\ pi\\ \ aprox 153.86 \ end {array}\) |
Calcular el volumen, utilizando 3.14 como aproximación para\(\ \pi\). |
El volumen es de 49\(\ \pi\) o aproximadamente\(\ 153.86 \text { feet }^{3}\).
Encuentra el volumen de un prisma rectangular que mide 8 pulgadas de largo, 3 pulgadas de ancho y 10 pulgadas de alto.
- \(\ 24 \text { inches}^{2}\)
- \(\ 30 \text { inches}^{2}\)
- \(\ 240 \text { inches}^{3}\)
- \(\ 720 \text { inches}^{3}\)
- Contestar
-
- Incorrecto. Parece que multiplicaste 8 pulgadas por 3 pulgadas para llegar a\(\ 24 \text { inches}^{2}\). Esta es el área de la base, no el volumen del prisma rectangular. La respuesta correcta es\(\ 240 \text { inches}^{3}\).
- Incorrecto. Parece que multiplicaste 3 pulgadas por 10 pulgadas para llegar a\(\ 30 \text { inches}^{2}\). Esta es el área de una cara del prisma rectangular, no el volumen del prisma rectangular. La respuesta correcta es\(\ 240 \text { inches}^3\).
- Correcto. Para encontrar el volumen del prisma rectangular, use la fórmula\(\ V=l \cdot w \cdot h\) y luego sustituya en los valores la longitud, la anchura y la altura. \(\ 8 \text{ inches }\cdot 3\text{ inches }\cdot 10\text{ inches }=240 \text{ inches}^3\).
- Incorrecto. Vuelve a verificar tu multiplicación. Para encontrar el volumen del prisma rectangular, use la fórmula\(\ V=l \cdot w \cdot h\) y luego sustituya en los valores la longitud, la anchura y la altura. La respuesta correcta es\(\ 240 \text { inches}^3\).
Sólidos compuestos
Los sólidos geométricos compuestos están hechos de dos o más sólidos geométricos. También puede encontrar el volumen de estos sólidos, siempre y cuando pueda averiguar los sólidos individuales que componen la forma compuesta.
Mira la imagen de una cápsula a continuación. Cada extremo es una media esfera. Se puede encontrar el volumen del sólido desarmándolo. ¿En qué sólidos puedes romper esta forma?
Se puede romper en un cilindro y dos medias esferas.
Dos medias esferas forman una entera, así que si conoces las fórmulas de volumen para un cilindro y una esfera, puedes encontrar el volumen de esta cápsula.
Si el radio de los extremos esféricos es de 6 pulgadas, encuentra el volumen del sólido debajo. Use 3.14 para\(\ \pi\). Redondea tu respuesta final al número entero más cercano.
Solución
 |
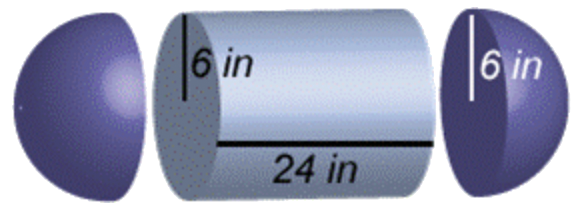Identificar los sólidos compuestos. Esta cápsula puede ser pensada como un cilindro con una media esfera en cada extremo. |
|
Volumen de un cilindro:\(\ \pi \cdot r^{2} \cdot h\) Volumen de una esfera:\(\ \frac{4}{3} \pi r^{3}\) |
Identificar las fórmulas adecuadas a utilizar. |
|
Volumen de un cilindro:\(\ \pi \cdot 6^{2} \cdot 24\) Volumen de una esfera:\(\ \frac{4}{3} \pi \cdot 6^{3}\) |
Sustituir las dimensiones en las fórmulas. La altura de un cilindro se refiere a la sección entre las dos bases circulares. Esta dimensión se da como 24 pulgadas, entonces\(\ h=24\). |
|
Volumen del cilindro: \ (\\ comenzar {alineado} Volumen de la esfera: \ (\\ comenzar {alineado} |
El radio de la esfera es de 6 pulgadas. Se puede utilizar\(\ r=6\) en ambas fórmulas. Calcular el volumen del cilindro y la esfera. |
|
Volumen de la cápsula: \(\ 2712.96+904.32 \approx 3617.28\) |
Agregar los volúmenes. |
El volumen de la cápsula es\(\ 1,152 \pi\) o aproximadamente\(\ 3617 \text { inches}^{3}\).
Un escultor talla un prisma rectangular a partir de una pieza sólida de madera. Entonces, en la parte superior, ahuecó una pirámide invertida. El sólido, y sus dimensiones, se muestran a la derecha. ¿Cuál es el volumen de la pieza terminada?
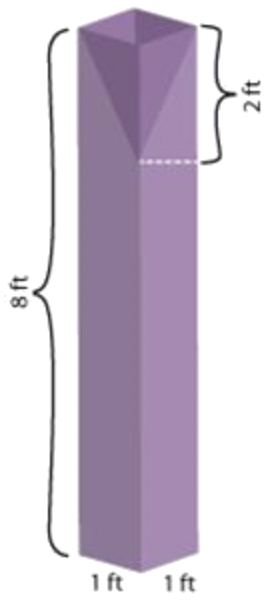
Solución
| Identificar los sólidos compuestos. Esta escultura puede pensarse como un prisma rectangular con una pirámide quitada. | |
| Volumen del prisma rectangular:\(\ l \cdot w \cdot h\) | Identificar las fórmulas adecuadas a utilizar. |
| Volumen de pirámide:\(\ \frac{l \cdot w \cdot h}{3}\) | |
|
Volumen del prisma rectangular:\(\ 1 \cdot 1 \cdot 8=8\) Volumen de pirámide:\(\ \frac{1 \cdot 1 \cdot 2}{3}=\frac{2}{3}\) |
Sustituir las dimensiones en las fórmulas, y calcular. |
| Volumen de escultura:\(\ V=8-\frac{2}{3}=7\frac{1}{3}\) | Restar el volumen de la pirámide del volumen del prisma rectangular. |
El volumen de la escultura es\(\ 7 \frac{1}{3} \text { feet }^{3}\).
Una máquina toma un cilindro sólido con una altura de 9 mm y un diámetro de 7 mm, y perfora un agujero a través de él. El agujero que crea tiene un diámetro de 3mm. ¿Cuál de las siguientes expresiones encontraría correctamente el volumen del sólido?
- \(\ \left(\pi \cdot 7^{2} \cdot 9\right)-\left(\pi \cdot 3^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)-\left(\pi \cdot 1.5^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 7^{2} \cdot 9\right)+\left(\pi \cdot 3^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)+\left(\pi \cdot 1.5^{2} \cdot 9\right)\)
- Contestar
-
- Incorrecto. Recuerda que la fórmula para el volumen de un cilindro es\(\ \pi r^{2} h\), no\(\ \pi d^{2} h\). La respuesta correcta es\(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)-\left(\pi \cdot 1.5^{2} \cdot 9\right)\).
- Correcto. Encuentras el volumen de todo el cilindro multiplicando\(\ \pi \cdot 3.5^{2} \cdot 9\), luego restas el cilindro vacío en el medio, que se encuentra multiplicando\(\ \pi \cdot 1.5^{2} \cdot 9\).
- Incorrecto. Recuerda que la fórmula para el volumen de un cilindro es\(\ \pi r^{2} h\), no\(\ \pi d^{2} h\). Además, debes restar el volumen del cilindro interior del volumen del cilindro exterior, no agregarlo. La respuesta correcta es\(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)-\left(\pi \cdot 1.5^{2} \cdot 9\right)\).
- Incorrecto. Has calculado los volúmenes correctos para los cilindros exterior e interior, pero debes restar el interior del exterior en lugar de sumarlos. La respuesta correcta es\(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)-\left(\pi \cdot 1.5^{2} \cdot 9\right)\).
Resumen
Los sólidos tridimensionales tienen longitud, anchura y altura. Se utiliza una medida llamada volumen para determinar la cantidad de espacio que ocupan estos sólidos. Para encontrar el volumen de un sólido geométrico específico, puede usar una fórmula de volumen que sea específica de ese sólido. En ocasiones, encontrarás sólidos geométricos compuestos. Se trata de sólidos que combinan dos o más sólidos básicos. Para encontrar el volumen de estos, identificar los sólidos más simples que componen la figura compuesta, encontrar los volúmenes de esos sólidos y combinarlos según sea necesario.