9.3.1: Propiedades asociativas, conmutativas y distributivas
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identificar y utilizar las propiedades conmutativas para la adición y multiplicación.
- Identificar y utilizar las propiedades asociativas para la suma y multiplicación.
- Identificar y utilizar la propiedad distributiva.
Introducción
Hay muchas veces en álgebra cuando se necesita simplificar una expresión. Las propiedades de los números reales proporcionan herramientas para ayudarle a tomar una expresión complicada y simplificarla.
Las propiedades asociativas, conmutativas y distributivas del álgebra son las propiedades más utilizadas para simplificar las expresiones algebraicas. Querrás tener una buena comprensión de estas propiedades para que los problemas en álgebra sean más fáciles de resolver.
Las propiedades conmutativas de la suma y la multiplicación
Puede encontrar rutinas diarias en las que se puede cambiar el orden de las tareas sin cambiar el resultado. Por ejemplo, piensa en servir una taza de café por la mañana. Acabarías con la misma sabrosa taza de café ya sea que agregaras los ingredientes de alguna de las siguientes maneras:
- Vierte 12 onzas de café en la taza, luego agrega un chorrito de leche.
- Agrega un chorrito de leche a la taza, luego agrega 12 onzas de café.
El orden en que añadas los ingredientes no importa. De la misma manera, no importa si primero te pones tu zapato izquierdo o derecho antes de salir a trabajar. Siempre y cuando estés usando ambos zapatos cuando salgas de tu casa, ¡estás en el camino correcto!
En matemáticas, decimos que estas situaciones son conmutativas—el resultado será el mismo (el café se prepara a tu gusto; sales de casa con ambos zapatos puestos) sin importar el orden en que se realicen las tareas.
De igual manera, la propiedad conmutativa de suma establece que cuando se están sumando dos números, su orden se puede cambiar sin afectar la suma. Por ejemplo, 30+25 tiene la misma suma que 25+30.
30+25=55
25+30=55
La multiplicación se comporta de manera similar. La propiedad conmutativa de la multiplicación establece que cuando se multiplican dos números, su orden se puede cambiar sin afectar al producto. Por ejemplo, 7⋅12 tiene el mismo producto que 12⋅7.
7⋅12=84
12⋅7=84
Estas propiedades se aplican a todos los números reales. Echemos un vistazo a algunos ejemplos adicionales.
| Ecuación Original | Ecuación reescrita |
| 1.2+3.8=5 | 3.8+1.2=5 |
| 12+18=58 | 18+12=58 |
| 14+(−10)=4 | (−10)+14=4 |
| 13+(−123)=−113 | (−123)+13=−113 |
| (−5.2)+(−3.6)=−8.8 | (−3.6)+(−5.2)=−8.8 |
Para cualquier número real a y b, a+b=b+a.
La resta no es conmutativa. Por ejemplo, 4−7 no tiene la misma diferencia que 7−4. El − signo aquí significa resta.
No obstante, recordemos que se 4−7 puede reescribir como 4+(−7), ya que restar un número es lo mismo que sumar su opuesto. Aplicando la propiedad conmutativa para la adición aquí, se puede decir que 4+(−7) es lo mismo que (−7)+4. Observe como esta expresión es muy diferente a 7−4.
Ahora mira algunos ejemplos de multiplicación.
| Ecuación Original | Ecuación reescrita |
| 4.5⋅2=9 | 2⋅4.5=9 |
| (−5)⋅3=−15 | 3⋅(−5)=−15 |
| 15⋅5=1 | 5⋅15=1 |
| (−14)⋅(−810)=15 | (−810)⋅(−14)=15 |
Para cualquier número real a y b, a⋅b=b⋅a.
El orden no importa siempre y cuando las dos cantidades se estén multiplicando juntas. Esta propiedad funciona para números reales y para variables que representan números reales.
Así como la resta no es conmutativa, tampoco la división es conmutativa. 4÷2no tiene el mismo cociente que 2÷4.
Escribe la expresión de una (−15.5)+35.5 manera diferente, usando la propiedad conmutativa de suma, y muestra que ambas expresiones dan como resultado la misma respuesta.
Solución
| (−15.5)+35.5=20 | Añadiendo. |
| 35.5+(−15.5) | Usando la propiedad conmutativa, puede cambiar el -15.5 y el 35.5 para que estén en un orden diferente. |
| \ (\\ begin {array} {c} 35.5+ (-15.5)\\ 35.5-15.5=20 \ end {array}\) |
Sumar 35.5 y -15.5 es lo mismo que restar 15.5 de 35.5. La suma es 20. |
(−15.5)+35.5=20y 35.5+(−15.5)=20
Reescribir 52⋅y de una manera diferente, utilizando la propiedad conmutativa de la multiplicación. Tenga en cuenta que y representa un número real.
- 5y⋅2
- 52y
- 26⋅2⋅y
- y⋅52
- Contestar
-
- Incorrecto. No se puede cambiar un dígito de 52 y adjuntarlo a la variable y. La respuesta correcta es y⋅52.
- Incorrecto. Esta es otra forma de reescribir 52⋅y, pero no se ha utilizado la propiedad conmutativa. La respuesta correcta es y⋅52.
- Incorrecto. No es necesario tener en cuenta 52 en 26⋅2. La respuesta correcta es y⋅52.
- Correcto. Se invierte el orden de los factores.
Las propiedades asociativas de la suma y la multiplicación
La propiedad asociativa de suma establece que los números en una expresión de suma se pueden agrupar de diferentes maneras sin cambiar la suma. Puedes recordar el significado de la propiedad asociativa recordando que cuando te asocias con familiares, amigos y compañeros de trabajo, terminas formando grupos con ellos.
A continuación se presentan dos formas de simplificar el mismo problema de adición. En el primer ejemplo, 4 se agrupa con 5, y 4+5=9.
4+5+6=9+6=15
Aquí, el mismo problema se trabaja agrupando 5 y 6 primero, 5+6=11.
4+5+6=4+11=15
En ambos casos, la suma es la misma. Esto ilustra que al cambiar la agrupación de números al sumar se obtiene la misma suma.
Los matemáticos suelen utilizar paréntesis para indicar qué operación debe realizarse primero en una ecuación algebraica. Aquí se reescriben los problemas de adición de arriba, esta vez usando paréntesis para indicar la agrupación asociativa.
(4+5)+6=9+6=15
4+(5+6)=4+11=15
Es claro que los paréntesis no afectan a la suma; la suma es la misma independientemente de dónde se coloquen los paréntesis.
Para cualquier número real a b, y c,
(a+b)+c=a+(b+c).
El siguiente ejemplo muestra cómo se puede utilizar la propiedad asociativa para simplificar expresiones con números reales.
Reescribir 7+2+8.5−3.5 de dos maneras diferentes usando la propiedad asociativa de suma. Mostrar que las expresiones dan la misma respuesta.
Solución
|
\ (\\ begin {array} {r} |
La propiedad asociativa no se aplica a expresiones que implican sustracción. Entonces, reescribe la expresión como suma de un número negativo. |
| \ (\\ begin {array} {r} (7+2) +8.5+ (-3.5)\\ 9+8.5+ (-3.5)\\ 17.5+ (-3.5)\\ 17.5+ (-3.5)\ 17.5-3.5=14 \ end {array}\) |
Grupo 7 y 2, y sumarlos juntos. Después, agregue 8.5 a esa suma. Por último, sumar -3.5, que es lo mismo que restar 3.5. Restar 3.5. La suma es 14. |
| \ (\\ begin {array} {r} 7+2+ (8.5+ (-3.5))\\ 7+2+5\\ 9+5 \ end {array}\) |
Agrupar 8.5 y -3.5, y sumarlos juntos para obtener 5. Después agrega 7 y 2, y agrega esa suma al 5. La suma es 14. |
(7+2)+8.5−3.5=14y 7+2+(8.5+(−3.5))=14
La multiplicación tiene una propiedad asociativa que funciona exactamente igual que la de suma. La propiedad asociativa de la multiplicación establece que los números en una expresión de multiplicación pueden reagruparse usando paréntesis. Por ejemplo, la siguiente expresión se puede reescribir de dos maneras diferentes usando la propiedad asociativa.
Expresión original: −52⋅6⋅4
Expresión 1: (−52⋅6)⋅4=(−302)⋅4=−15⋅4=−60
Expresión 2: −52⋅(6⋅4)=−52⋅24=−1202=−60
Los paréntesis no afectan al producto. El producto es el mismo independientemente de dónde estén los paréntesis.
Para cualquier número real a, b, y c, (a⋅b)⋅c=a⋅(b⋅c).
Reescribir 12⋅(56⋅6) usando sólo la propiedad asociativa.
- (12⋅56)⋅6
- (56⋅6)⋅12
- 6⋅(56⋅12)
- 12⋅5
- Contestar
-
- Correcto. Aquí, los números se reagrupan. Ahora 12 y 56 se agrupan entre paréntesis en lugar de 56 y 6.
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión usando la propiedad asociativa de multiplicación. La forma en que se agrupan debe cambiar. La respuesta correcta es (12⋅56)⋅6.
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión usando la propiedad asociativa de multiplicación. Sólo la forma en que se agrupan debe cambiar. La respuesta correcta es (12⋅56)⋅6.
- Incorrecto. Multiplicar entre paréntesis no es una aplicación de la propiedad. La respuesta correcta es (12⋅56)⋅6.
Uso de las propiedades asociativas y conmutativas
Encontrarás que las propiedades asociativas y conmutativas son herramientas útiles en álgebra, especialmente cuando evalúas expresiones. Usando las propiedades conmutativa y asociativa, puede reordenar los términos en una expresión para que los números compatibles estén uno al lado del otro y se agrupen juntos. Los números compatibles son números que son fáciles de calcular para usted, como 5+5, o 3⋅10, o 12−2, o 100÷20. (El criterio principal para los números compatibles es que “funcionen bien” juntos). Los dos ejemplos a continuación muestran cómo se hace esto.
Evaluar la expresión 4⋅(x⋅27) cuando x=−34.
Solución
| 4⋅(x⋅27) | Expresión original. |
| 4⋅((−34)⋅27) | Sustituto −34 de x. |
| \ (\\ begin {array} {r} \ izquierda (4\ cdot\ izquierda (-\ frac {3} {4}\ derecha)\ derecha)\ cdot 27\ \ izquierda (-\ frac {12} {4}\ derecha)\ cdot 27 \ end {array}\) |
Utilice la propiedad asociativa de la multiplicación para reagrupar los factores de manera que 4 y −34 estén uno al lado del otro. Multiplicar 4 por −34 primero hace que la expresión sea un poco más fácil de evaluar que multiplicar −34 por 27. |
| −3⋅27=−81 | Multiplicar. 4tiempos −34=−3, y −3 tiempos 27 es −81. |
4⋅(x⋅27)=−81cuando x=(−34)
Simplificar: 4+12+3+4−8
Solución
| 4+12+3+4−8 | Expresión original. |
| 12+3+4+4+(−8) | Identificar números compatibles. 4+4es 8, y hay un −8. presente. Recordemos que se puede pensar en −8 como +(−8). Utilice la propiedad conmutativa de adición para agruparlos. |
| 12+3+(4+4+(−8)) | Utilice la propiedad asociativa para agrupar 4+4+(−8). |
| 12+3+0 | Agregar 4+4+(−8). |
| 12+3+0=15 | Agrega el resto de los términos. |
4+12+3+4−8=15
Simplifica la expresión: −5+25−15+2+8
- 5
- 15
- 30
- 55
- Contestar
-
- Incorrecto. Cuando utilice la propiedad conmutativa para reorganizar los apéndices, asegúrese de que los agregados negativos lleven sus signos negativos. La respuesta correcta es 15.
- Correcto. Utilice la propiedad conmutativa para reorganizar la expresión de modo que los números compatibles estén uno al lado del otro y, a continuación, utilice la propiedad asociativa para agruparlos.
- Incorrecto. Comprueba tu suma y resta, y piensa en el orden en el que estás sumando estos números. Utilice la propiedad conmutativa para reorganizar los agregados de manera que los números compatibles estén uno al lado del otro. La respuesta correcta es 15.
- Incorrecto. Parece que ignoraste los signos negativos aquí. Cuando utilice la propiedad conmutativa para reorganizar los apéndices, asegúrese de que los agregados negativos lleven sus signos negativos. La respuesta correcta es 15.
La propiedad distributiva
La propiedad distributiva de multiplicación es una propiedad muy útil que permite reescribir expresiones en las que está multiplicando un número por una suma o diferencia. El inmueble establece que el producto de una suma o diferencia, tal como 6(5−2), es igual a la suma o diferencia de productos, en este caso, 6(5)−6(2).
\ (\\ begin {array} {l}
6 (5-2) =6 (3) =18\\
6 (5) -6 (2) =30-12=18
\ end {array}\)
La propiedad distributiva de la multiplicación se puede utilizar cuando se multiplica un número por una suma. Por ejemplo, supongamos que desea multiplicar 3 por la suma de 10+2.
3(10+2)=?
Según esta propiedad, se pueden sumar los números 10 y 2 primero y luego multiplicar por 3, como se muestra aquí: 3(10+2)=3(12)=36. Alternativamente, primero puedes multiplicar cada adenda por el 3 (esto se llama distribuir el 3), y luego puedes agregar los productos. Este proceso se muestra aquí.
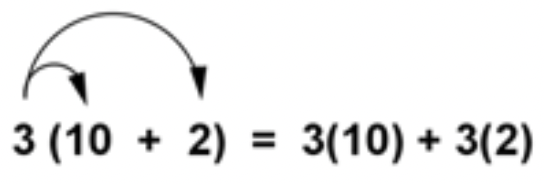
\ (\\ begin {array} {l}
3 (10+2) =3 (12) =36\\
3 (10) +3 (2) =30+6=36
\ end {array}\)
Los productos son los mismos.
Dado que la multiplicación es conmutativa, se puede utilizar la propiedad distributiva independientemente del orden de los factores.
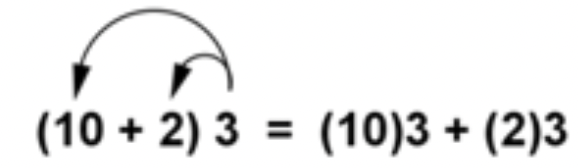
Para cualquier número real a b, y c:
La multiplicación distribuye sobre la suma:
a(b+c)=ab+ac
La multiplicación distribuye sobre la resta:
a(b−c)=ab−ac
Reescriba la expresión 10(9−6) usando la propiedad distributiva.
- 10(6)−10(9)
- 10(3)
- 10(6−9)
- 10(9)−10(6)
- Contestar
-
- Incorrecto. Dado que la resta no es conmutativa, no se puede cambiar el orden. La respuesta correcta es 10(9)−10(6).
- Incorrecto. Esta es una forma correcta de encontrar la respuesta. Pero la pregunta le pidió que reescribiera el problema usando la propiedad distributiva. La respuesta correcta es 10(9)−10(6)
- Incorrecto. Cambiaste el orden del 6 y el 9. Tenga en cuenta que la resta no es conmutativa y no utilizó la propiedad distributiva. La respuesta correcta es 10(9)−10(6).
- Correcto. El 10 se distribuye correctamente para que se utilice para multiplicar el 9 y el 6 por separado.
Distribuir con variables
Siempre y cuando las variables representen números reales, la propiedad distributiva se puede usar con variables. La propiedad distributiva es importante en álgebra, y a menudo verá expresiones como esta: 3(x−5). Si se le pide que amplíe esta expresión, puede aplicar la propiedad distributiva tal como lo haría si estuviera trabajando con enteros.
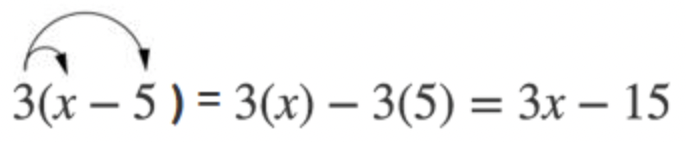
Recuerda, cuando multiplicas un número y una variable, solo puedes escribirlos uno al lado del otro para expresar la cantidad multiplicada. Entonces, la expresión “tres veces la variable x” se puede escribir de varias maneras: 3x, 3(x), o 3⋅x.
Utilice la propiedad distributiva para expandir la expresión 9(4+x).
Solución
| 9(4+x) | Expresión original. |
| 9(4)+9(x) | Distribuir el 9 y multiplicar. |
| 36+9x | Multiplicar. |
9(4+x)=36+9x
Utilice la propiedad distributiva para evaluar la expresión 5(2x−3) when x=2.
Solución
| 5(2x−3) | Expresión original. |
| 5(2x)−5(3) | Distribuir el 5. |
| 10x−15 | Multiplicar. |
|
10(2)−15 20−15=5 |
Sustituir 2 por x, y evaluar. |
Cuando x=2,5(2x−3)=5.
En el ejemplo anterior, ¿qué crees que pasaría si sustituyeras x=2 antes de distribuir el 5? ¿Obtendrías la misma respuesta de 5? El siguiente ejemplo muestra lo que sucedería.
Utilice la propiedad distributiva para evaluar la expresión 5(2x−3) when x=2.
Solución
| 5(2x−3) | Expresión original. |
| 5(2(2)−3) | Sustituto 2 para x. |
| \ (\\ begin {array} {c} 5 (4-3)\\ 5 (4) -5 (3) \ end {array}\) |
Multiplicar. |
| 20−15=5 | Restar y evaluar. |
Cuando x=2,5(2x−3)=5.
Combinando términos similares
La propiedad distributiva también puede ayudarte a entender una idea fundamental en álgebra: que cantidades como 3x y se 12x pueden sumar y restar de la misma manera que los números 3 y 12. Veamos un ejemplo y veamos cómo se puede hacer.
Agregar: 3x+12x
Solución
| 3(x)+12(x) | 3xes 3 veces x, y 12x es 12 veces x |
| x(3+12) | De estudiar la propiedad distributiva (y también usar la propiedad conmutativa), sabes que x(3+12) es lo mismo que 3(x)+12(x). |
| \ (\\ begin {array} {c} x (15)\\ \ text {o}\\ 15 x \ end {array}\) |
Combina los términos entre paréntesis: 3+12=15. |
3x+12x=15x
¿Ves lo que pasó? Al pensar en el x como una cantidad distribuida, se puede ver eso 3x+12x=15x. (Si no estás seguro de esto, intenta sustituir cualquier número por en esta expresión... ¡encontrarás que es cierto!)
Los grupos de términos que consisten en un coeficiente multiplicado por la misma variable se denominan “términos similares”. La siguiente tabla muestra algunos grupos diferentes de términos similares:
| Grupos de términos similares |
| 3x,7x,−8x,−0.5x |
| −1.1y,−4y,−8y |
| 12t,25t,100t,1t |
| 4ab,−8ab,2ab |
Siempre que veas términos similares en una expresión o ecuación algebraica, puedes sumarlos o restarlos tal como sumarías o restarías números reales. Entonces, por ejemplo,
10y+12y=22y, y 8x−3x−2x=3x.
Ten cuidado de no combinar términos que no tengan la misma variable: 6xy ¡no lo 4x+2y es!
Simplificar: 10y+5y+9x−6x−x.
Solución
| 10y+5y+9x−6x−x | Hay términos similares en esta expresión, ya que todos consisten en un coeficiente multiplicado por la variable x o y. Tenga en cuenta que −x es lo mismo que (−1)x. |
| 15y+2x | Agregar términos similares. 10y+5y=15y, y 9x−6x−x=2x. |
10y+5y+9x−6x−x=15y+2x
Simplificar: 12x−x+2x−8x.
- 23x
- 5
- 5x
- x
- Contestar
-
- Incorrecto. Parece que agregaste todos los términos. Observe que −x y −8x son negativos. La respuesta correcta es 5x.
- Incorrecto. Combinaste los enteros correctamente, ¡pero recuerda incluir también la variable! La respuesta correcta es 5x.
- Correcto. Cuando combinas estos términos similares, terminas con una suma de 5x
- Incorrecto. Parece que le restaste todos los términos 12x. Observe que −x y −8x son negativos, pero eso 2x es positivo. La respuesta correcta es 5x.
Resumen
Las propiedades conmutativas, asociativas y distributivas le ayudan a reescribir una expresión algebraica complicada en una que sea más fácil de tratar. Cuando reescribe una expresión por una propiedad conmutativa, cambia el orden de los números que se agregan o multiplican. Cuando reescribe una expresión usando una propiedad asociativa, agrupa un par diferente de números usando paréntesis. Se pueden utilizar las propiedades conmutativas y asociativas para reagrupar y reordenar cualquier número en una expresión siempre que la expresión esté compuesta completamente por adiciones o factores (y no una combinación de ellos). La propiedad distributiva se puede utilizar para reescribir expresiones para una variedad de propósitos. Cuando estás multiplicando un número por una suma, puedes sumar y luego multiplicar. También puedes multiplicar primero cada adenda y luego sumar los productos juntos. El mismo principio se aplica si estás multiplicando un número por una diferencia.


