15.3.1: Fórmulas racionales y variación
- Page ID
- 111207
- Resolver una fórmula para una letra especificada.
- Identificar variación directa, inversa y conjunta.
- Encuentra lo desconocido en un problema de variación.
- Resolver problemas de aplicación que involucran variación directa.
- Resolver problemas de aplicación que involucran variación inversa.
- Resolver problemas de aplicación que involucran variación articular.
Introducción
Las fórmulas racionales pueden ser herramientas útiles para representar situaciones de la vida real y para encontrar respuestas a problemas reales. Las ecuaciones que representan variación directa, inversa y conjunta son ejemplos de fórmulas racionales que pueden modelar muchas situaciones de la vida real. Como verás, si puedes encontrar una fórmula, normalmente puedes darle sentido a una situación.
Trabajar con Fórmulas
Al resolver problemas usando fórmulas racionales, a menudo es útil resolver primero la fórmula para la variable especificada. Por ejemplo, los problemas laborales te piden calcular cuánto tiempo tardará a diferentes personas trabajando a diferentes velocidades para terminar una tarea. Los modelos algebraicos de tales situaciones a menudo involucran ecuaciones racionales derivadas de la fórmula de trabajo,\(\ W=r t\). La cantidad de trabajo realizado\(\ (W)\) es producto de la tasa de trabajo\(\ (r)\) y del tiempo dedicado a trabajar\(\ (t)\). Usando álgebra, puedes escribir la fórmula de trabajo de 3 maneras:
\ (\\ begin {array} {c}
w=r t\
\ text {Encuentra el tiempo} (t). t=\ frac {W} {r} (\ text {divide ambos lados por} r)\\
\ text {Encuentra la tasa} (r). r=\ frac {W} {t} (\ text {divide ambos lados por} t)
\ end {array}\)
La fórmula para encontrar la densidad de un objeto es\(\ D=\frac{m}{v}\), donde\(\ D\) está la densidad,\(\ m\) es la masa del objeto y\(\ v\) es el volumen del objeto. Reorganice la fórmula para resolver para la masa\(\ (m)\) y luego para el volumen\(\ (v)\).
Solución
| \(\ D=\frac{m}{v}\) | Comience con la fórmula para la densidad. |
| \(\ v \cdot D=\frac{m}{v} \cdot v\) | Multiplique ambos lados de la ecuación por\(\ v\) para aislar\(\ m\). |
| \ (\\ begin {array} {c} v\ cdot d=M\ cdot\ frac {v} {v}\\ v\ cdot d=M\ cdot 1\\ v\ cdot d=M \ end {array}\) |
Simplifique y reescriba la ecuación, resolviendo para\(\ m\). |
| \ (\\ begin {array} {c} \ frac {v\ cdot D} {D} =\ frac {m} {D}\ \ frac {D} {D}\ cdot v =\ frac {m} {D} {D}\ 1\ cdot v =\ frac {m} {D} {D}\ v=\ frac {m} {D} \ end {array}\) |
Para resolver la ecuación\(\ D=\frac{m}{v}\) en términos de\(\ v\), necesitarás hacer los mismos pasos hasta este punto, y luego dividir ambos lados por\(\ D\). |
Ahora veamos un ejemplo usando la fórmula para el volumen de un cilindro.
La fórmula para encontrar el volumen de un cilindro es\(\ V=\pi r^{2} h\), donde\(\ V\) está el volumen,\(\ r\) es el radio y\(\ h\) es la altura del cilindro. Reorganice la fórmula para resolver la altura\(\ (h)\).
Solución
| \(\ V=\pi r^{2} h\) | Comienza con la fórmula para el volumen de un cilindro. |
| \ (\\ begin {array} {l} \ frac {V} {\ pi r^ {2}} =\ frac {\ pi r^ {2} h} {\ pi r^ {2}}\ \ frac {V} {\ pi r^ {2}} =h \ end {array}\) |
Divide ambos lados por\(\ \pi r^{2}\) para aislarlos\(\ h\). Simplificar. Encuentras la altura,\(\ h\), Simplifica. Encuentras la altura,\(\ \frac{V}{\pi r^{2}}\). |
\(\ h=\frac{V}{\pi r^{2}}\)
Variación directa
Las ecuaciones de variación son ejemplos de fórmulas racionales y se utilizan para describir la relación entre variables. Por ejemplo, imagina un estacionamiento lleno de autos. El número total de llantas en el estacionamiento depende del número total de autos. Álgebraicamente, se puede representar esta relación con una ecuación.
\(\ \text { Number of tires }=4 \cdot \text { number of cars }\)
El número 4 te indica la tasa a la que están relacionados los autos y las llantas. Llamas a la tasa la constante de variación. Es una constante porque este número no cambia. Debido a que el número de autos y el número de llantas están vinculados por una constante, los cambios en el número de autos hacen que el número de llantas cambie de manera proporcional y constante. Este es un ejemplo de variación directa, donde el número de llantas varía directamente con el número de autos.
Se puede utilizar la ecuación de automóvil y neumático como base para escribir una ecuación algebraica general que funcione para todos los ejemplos de variación directa. En el ejemplo, el número de llantas es la salida, 4 es la constante, y el número de autos es la entrada. Ingresemos esos términos genéricos en la ecuación. Obtienes:
\(\ \text { output }=\text { constant } \cdot \text { input }\)
Esa es la fórmula para todas las ecuaciones de variación directa.
\ (\\ begin {array} {c}
\ text {Número de llantas} =4\ cdot\ text {número de autos}\\
\ text {output} =\ text {constante}\ cdot\ text {input}
\ end {array}\)
Busquemos una manera general de representar la variación directa. Cuando empezamos a hablar de entrada y salida en una ecuación, a menudo llamamos a la ecuación una función. La salida de una función (ecuación) también se conoce como la variable dependiente y generalmente se representa simbólicamente como\(\ y\). La entrada se llama la variable independiente, representada por el símbolo\(\ x\). Representemos la constante con la letra\(\ k\). Ahora pon esos símbolos en la ecuación.
\ (\\ begin {array} {c}
\ text {número de llantas} =4\ cdot\ text {número de autos}\\
\ text {output} =\ text {constante}\ cdot\ text {input}\\
y=kx
\ end {array}\)
¡Y ya lo has hecho! Todas las ecuaciones de variación directa pueden ser descritas por la ecuación\(\ y=k x\).
Veamos otro ejemplo de variación directa. Mary trabaja en un puesto de carretera en la granja familiar de pollos, vendiendo huevos por $1.99 por caja los fines de semana ocupados. Cuando los clientes compran muchos cartones a la vez, tiene que sumar los totales con lápiz y papel, y se preocupa por cometer errores. Por suerte para Mary, esta es una relación de variación directa: la salida (costo total) es igual a la entrada (número de cajas) multiplicada por una constante (el precio por caja). Ella puede usar una ecuación de variación directa para hacer una tabla de precios para usar como atajo.
En este caso:
\(\ \text { total cost }=\text { carton price } \cdot \text { number of cartons. Total cost }=1.99 \cdot \text { number of cartons. }\)
| Número de cajas | Precio total |
| 1 | $1.99 |
| 2 | 3,98 |
| 3 | $5.97 |
| 4 | $7.96 |
| 5 | $9.95 |
| 6 | 11,94$ |
Vamos a graficar la función de costo del huevo/caja de cartón.
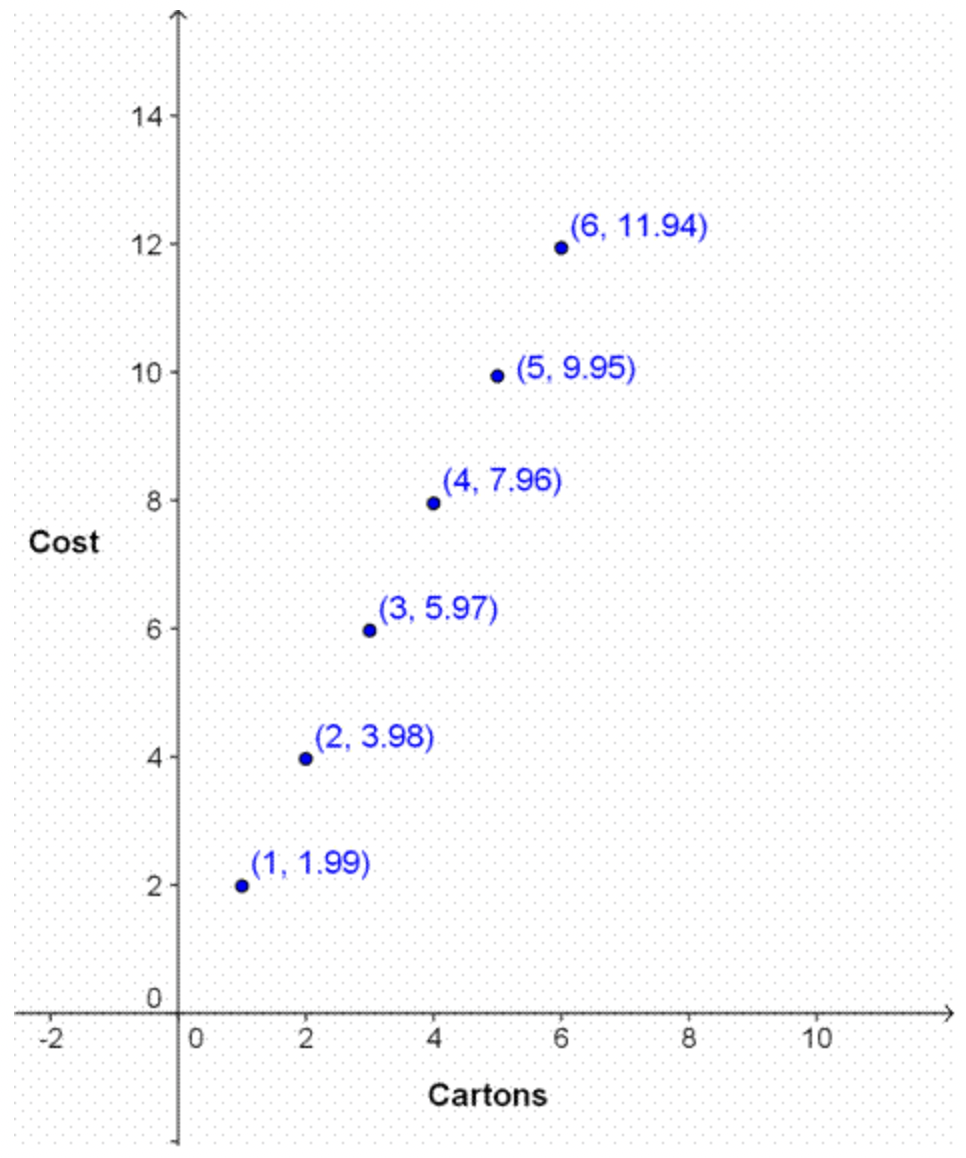
Esta función está conformada por puntos individuales porque el puesto de la granja solo vende cajas enteras de huevos. Pero se puede ver que todos los puntos están espaciados uniformemente, y parecen estar en línea recta. También se puede ver que aunque no está trazado, el punto\(\ (0,0)\) satisface la función. El costo de 0 cartones sería de 0 dólares.
Ahora veamos la gráfica de una ecuación de variación directa continua y veamos en qué se diferencia de la gráfica anterior. (En la gráfica de una función continua, existen puntos de datos individuales en cada punto de la línea, a diferencia del ejemplo de huevo anterior donde no tiene sentido hablar del precio de 1.235 cajas de huevos!)
Imagine que un grifo vierte agua en una tina a razón de 2.5 galones por minuto. La cantidad de agua en la tina varía directamente con la cantidad de tiempo que el grifo ha estado funcionando. Se puede representar la relación entre el tiempo y el agua en la tina con la siguiente fórmula.
\(\ \text { Total gallons of water }=2.5 \text { gallons of water/minute} \cdot \text{time in minutes}\)
Utilizando\(\ g\) para representar galones totales de agua y\(\ t\) para representar el tiempo, puede abreviar esta relación como\(\ g=2.5 t\), que se ve muy similar a la fórmula estándar para funciones proporcionales,\(\ y=k x\).
Hagamos una tabla para trazar la relación del tiempo versus la cantidad de agua en la tina. Después de 1 minuto, 2.5 galones están en la tina. Después de 2 minutos, el total es de 5 galones, y así sucesivamente. Para encontrar la cantidad total de agua en la tina en cualquier momento, puedes multiplicar el tiempo por 2.5 galones por minuto. Seis minutos deberían darte suficientes puntos para hacer una gráfica útil.
| Tiempo | Total de galones |
| 1 | 2.5 |
| 2 | 5.0 |
| 3 | 7.5 |
| 4 | 10.0 |
| 5 | 12.5 |
| 6 | 15.0 |
Ahora puedes graficar esos puntos.
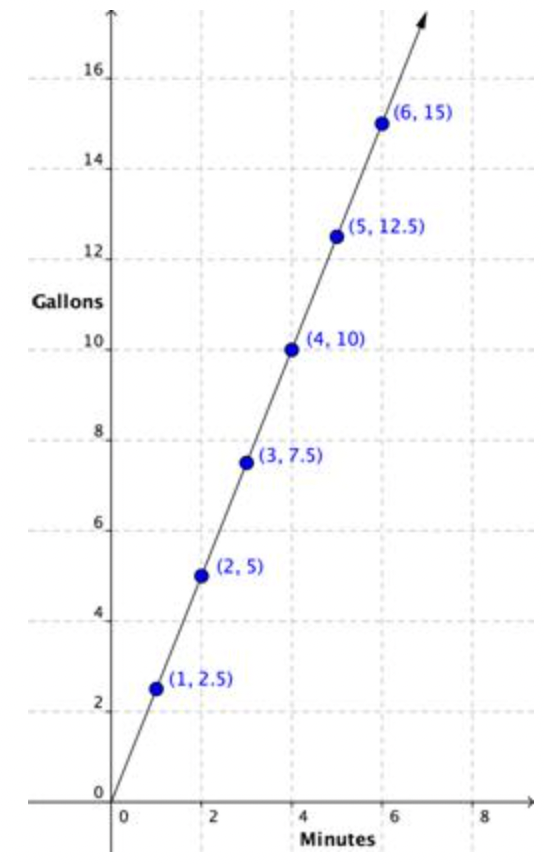
Esta vez, usa una línea para conectar los puntos, porque tanto el tiempo como el agua aumentan continuamente. Los puntos se encuentran en una línea recta que comienza en el origen y se eleva en un ángulo constante, al igual que la última gráfica. En el ejemplo de huevo, no tenía sentido comprar 2.5 cajas de huevos, por lo que no trazaste una línea para conectar los puntos. Pero con el ejemplo de agua, se puede medir el número total de galones después de 2.5 minutos, así que conectar los puntos tiene sentido.
Cuando las variables en una función cambian a una tasa constante como esta, tienen una relación proporcional. Esta tasa constante de cambio se llama la constante de variación.
Resolver para\(\ k\), la constante de variación, en un problema de variación directa donde\(\ y=300\) y\(\ x=10\).
Solución
| \(\ y=k x\) | Escribe la fórmula para una relación de variación directa. |
| \(\ 300=k \cdot 10\) | Sustituir valores conocidos en la ecuación. |
|
\(\ \frac{300}{10}=\frac{10 k}{10}\) \(\ 30=k\) |
Resuelve\(\ k\) dividiendo ambos lados de la ecuación por 10. |
La constante de variación,\(\ k\), es 30.
¿Qué línea a continuación es una gráfica que muestra la variación directa?
- Línea 1
- Línea 2
- Línea 3
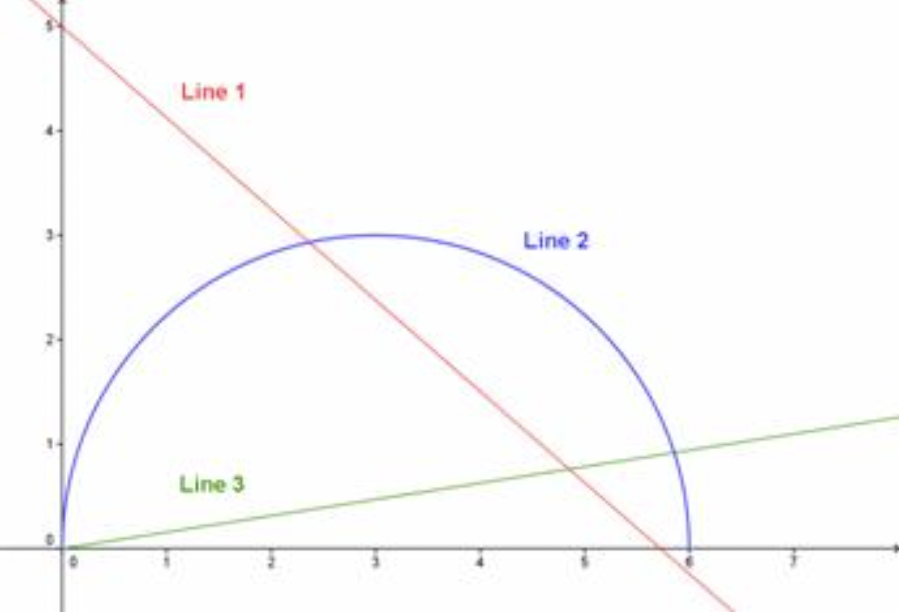
- Contestar
-
- Incorrecto. La línea 1 es una línea, pero no pasa por el origen. Esto significa que la relación no varía directamente. La respuesta correcta es la Línea 3.
- Incorrecto. La línea 2 es una curva, no una línea, por lo que no puede ser un ejemplo de variación directa. La respuesta correcta es la Línea 3.
- Correcto. La línea 3 es una línea que incluye el origen, lo que la convierte en un ejemplo de variación directa.
Variación inversa
Otro tipo de variación se llama variación inversa. En estas ecuaciones, la variable dependiente equivale a una constante dividida por la variable independiente. En forma simbólica, esta es la ecuación\(\ y=\frac{k}{x}\), donde\(\ y\) está la variable dependiente,\(\ k\) es la constante, y\(\ x\) es la variable independiente. Compare esto con la ecuación para una función que tenga variación directa entre las variables, como la fórmula de variación directa de\(\ y=k x\). La única diferencia es que la variable independiente está ahora en el denominador.
Un ejemplo de una variación inversa es la velocidad requerida para viajar entre dos ciudades en una cantidad de tiempo determinada.
Digamos que necesitas conducir de Boston a Chicago, que es de aproximadamente 1,000 millas. Cuanto más tiempo tengas, más lento podrás ir. Si quieres llegar en 20 horas, necesitas recorrer 50 millas por hora (¡suponiendo que no dejes de conducir!) , porque\(\ \frac{1,000}{20}=50\). Pero si puedes tardar 40 horas en llegar ahí, solo tienes que promediar 25 millas por hora, ya que\(\ \frac{1,000}{40}=25\).
La ecuación para averiguar qué tan rápido viajar a partir de la cantidad de tiempo que tienes es\(\ \text { speed }=\frac{\text { miles }}{\text { time }}\). Esta ecuación debería recordarte la fórmula de distancia\(\ d=r t\). Si resuelves\(\ d=r t\) por\(\ r\), obtienes\(\ r=\frac{d}{t}\), o\(\ \text { speed }=\frac{\text { miles }}{\text { time }}\).
En el caso del viaje de Boston a Chicago, puedes escribir\(\ s=\frac{1,000}{t}\). Observe que esta es la misma forma que la fórmula de la función de variación inversa,\(\ y=\frac{k}{x}\).
Aquí hay una tabla que muestra varios tiempos y velocidades que satisfacen la ecuación:
| Tiempo | Velocidad (millas por hora) |
| 1 | 1,000 |
| 5 | 200 |
| 10 | 100 |
| 12.5 | 80 |
| 20 | 50 |
| 25 | 40 |
| 40 | 25 |
Ahora bien, si trazas esos puntos, verás que la gráfica es definitivamente una curva, no una línea.
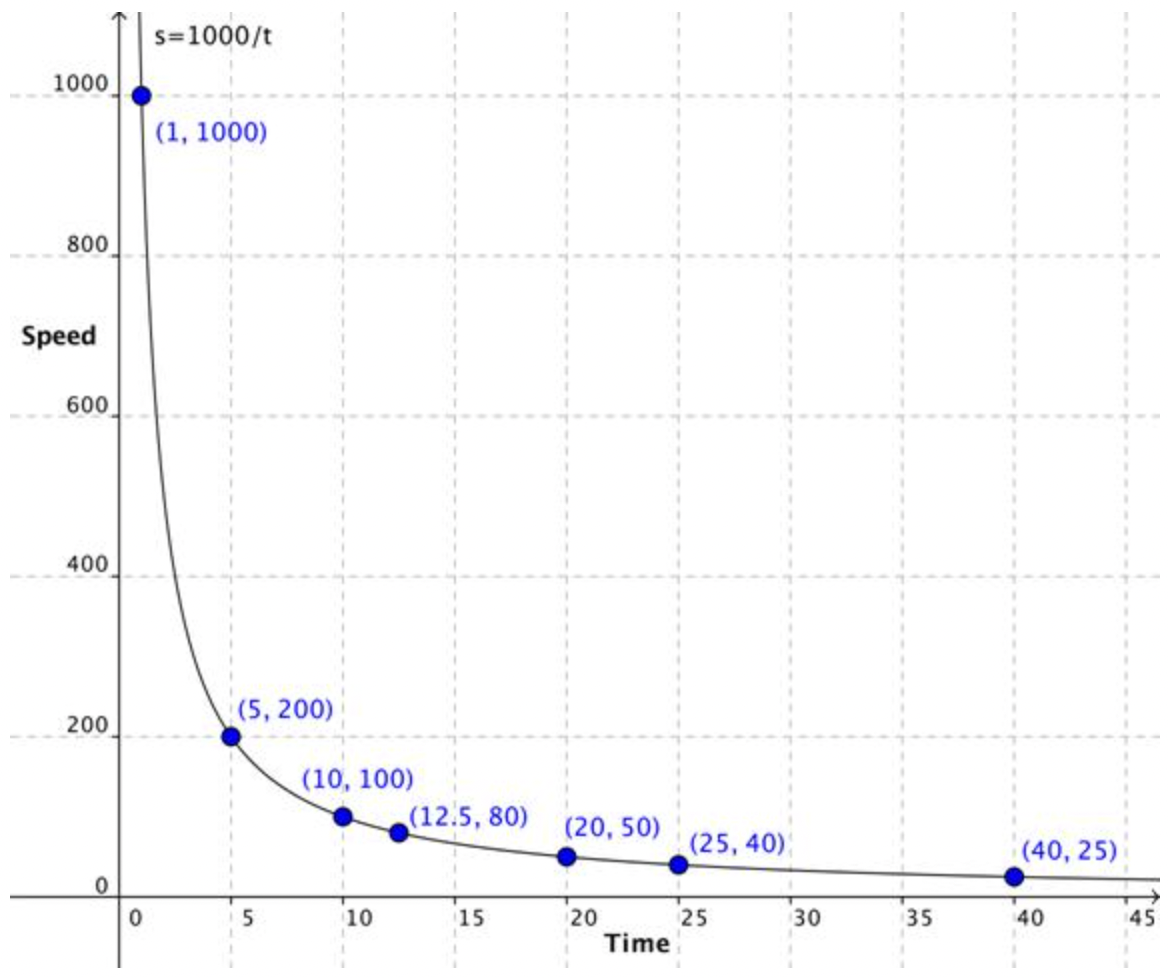
Resolver para\(\ k\), la constante de variación, en un problema de variación inversa donde\(\ x=5\) y\(\ y=25\).
Solución
| \(\ y=\frac{k}{x}\) | Escribe la fórmula para una relación de variación inversa. |
| \(\ 25=\frac{k}{5}\) | Sustituir valores conocidos en la ecuación. |
|
\ (\\ begin {array} {c} \(\ 125=k\) |
Resuelve\(\ k\) multiplicando ambos lados de la ecuación por 5. |
La constante de variación,\(\ k\), es 125.
La temperatura del agua en el océano varía inversamente con la profundidad del agua. Cuanto más profundo se sumerge una persona, más fría se vuelve el agua. A una profundidad de 1,000 metros, la temperatura del agua es de 5 o Celsius. ¿Cuál es la temperatura del agua a una profundidad de 500 metros?
Solución
| \ (\\ begin {array} {r} y=\ frac {k} {x}\\ \ text {temp} =\ frac {k} {\ text {profundidad}} \ end {array}\) |
Se le dice que esta es una relación inversa, y que la temperatura del agua\(\ (y)\) varía inversamente con la profundidad del agua\(\ (x)\). |
| \ (\\ begin {array} {r} 5=\ frac {k} {1,000}\\ 1,000\ cdot 5=\ frac {k} {1,000}\ cdot 1,000 \ end {array}\) |
Sustituir valores conocidos en la ecuación. |
| \ (\\ begin {array} {l} 5.000=\ frac {1,000 k} {1,000}\\ 5.000=k \ end {array}\) |
Resolver para\(\ k\). |
| \ (\\ begin {array} {l} \ texto {temp} =\ frac {k} {\ texto {profundidad}}\ \ texto {temp} =\ frac {5,000} {500}\ \ texto {temp} =10 \ end {array}\) |
Ahora que\(\ k\), se conoce la constante de variación, usa esa información para resolver el problema: encontrar la temperatura del agua a 500 metros. |
A 500 metros, la temperatura del agua es de 10 o Celsius.
En una función de variación inversa, ¿qué sucede con la salida a medida que la entrada se hace más pequeña?
- Se hace más grande.
- Se hace más pequeño.
- Contestar
-
- Correcto. Dado que la salida es una constante dividida por la entrada, a medida que disminuye la entrada, la constante se divide por un número cada vez más pequeño. Esto significa que en una función de variación inversa, la salida continúa aumentando a medida que la entrada se hace más pequeña.
- Incorrecto. En una función de variación directa, la salida se encogerá a medida que la entrada se contrae, pero justo lo contrario ocurre en una función de variación inversa. La respuesta correcta es que se hace más grande.
Variación conjunta
Un tercer tipo de variación se llama variación conjunta. La variación conjunta es lo mismo que la variación directa excepto que hay dos o más cantidades. Por ejemplo, el área de un rectángulo se puede encontrar usando la fórmula\(\ A=l w\), donde\(\ l\) está la longitud del rectángulo y\(\ w\) es el ancho del rectángulo. Si cambia el ancho del rectángulo, entonces el área cambia. Del mismo modo, si cambias la longitud del rectángulo, entonces el área también cambiará. Se puede decir que el área del rectángulo “varía conjuntamente con la longitud y el ancho del rectángulo”.
La fórmula para el volumen de un cilindro,\(\ V=\pi r^{2} h\) es otro ejemplo de variación conjunta. El volumen del cilindro varía conjuntamente con el cuadrado del radio y la altura del cilindro. La constante de variación es\(\ \pi\).
El área de un triángulo varía conjuntamente con las longitudes de su base y altura. Si el área de un triángulo es\(\ 30 \text { inches }^{2}\) cuando la base es de 10 pulgadas y la altura es de 6 pulgadas, encuentra la variación constante y el área de un triángulo cuya base es de 15 pulgadas y la altura es de 20 pulgadas.
Solución
| \(\ y=k x z\) | Se le dice que se trata de una relación de variación conjunta, y que el área de un triángulo\(\ (A)\) varía conjuntamente con las longitudes de la base\(\ (b)\) y la altura\(\ (h)\). |
| \ (\\ begin {array} {r} 30=k\ cdot 10\ cdot 6\\ 30=60 k\\ \ frac {30} {60} =\ frac {60 k} {60}\ \ frac {1} {2} =k \ end {array}\) |
Sustituir valores conocidos en la ecuación, y resolver para\(\ k\). |
| \ (\\ begin {array} {r} \ text {Área} =k\ cdot\ text {base}\ cdot\ text {altura}\ \ qquad\ begin {array} {c} \ text {Área} =( 15) (20)\ left (\ frac {1} {2}\ derecha)\ \ texto {Área} =\ frac {300} {2}\\ \ text {Área} =150\ texto {pulgadas cuadradas} \ end {array} \ end {array}\) |
Ahora que\(\ k\) se sabe, resuelva para el área de un triángulo cuya base es de 15 pulgadas y la altura es de 20 pulgadas. |
La constante de variación,\(\ k\), es\(\ \frac{1}{2}\), y el área del triángulo es de 150 pulgadas cuadradas.
Encontrar\(\ k\) ser no\(\ \frac{1}{2}\) debería ser sorprendente. Ya sabes que el área de un triángulo es media base por altura,\(\ A=\frac{1}{2} b h\). ¡El\(\ \frac{1}{2}\) en esta fórmula es exactamente lo mismo\(\ \frac{1}{2}\) que calculaste en este ejemplo!
\(\ k\)es la constante de variación. En todos los casos,\(\ k \neq 0\).
- Variación directa:\(\ y=k x\)
- Variación inversa:\(\ y=\frac{k}{x}\)
- Variación conjunta:\(\ y=k x z\)
Es importante poder distinguir si una aplicación está variando directa, inversamente o conjuntamente.
Una roca que pesa 120 libras en la Tierra pesa 20 libras en la superficie de la luna. De igual manera, un astronauta que pesa 240 libras en la Tierra pesará 40 libras en la luna. ¿Es este un ejemplo de variación directa, inversa o conjunta?
- Variación directa
- Variación inversa
- Variación conjunta
- Contestar
-
- Correcto. Estos pesos revelan variación directa. A medida que el peso de un artículo aumenta en la Tierra, también su peso aumentará en la superficie de la luna.
- Incorrecto. Si esto fuera una relación inversa, entonces a medida que aumentaba el peso de un ítem en la Tierra, su peso sobre la superficie de la luna caería. Este no es el caso. La respuesta correcta es la variación directa.
- Incorrecto. El problema sólo da dos variables: una entrada (peso en la Tierra) y una salida (peso en la luna). Si esto fuera un ejemplo de variación conjunta, se habrían presentado más variables. La respuesta correcta es la variación directa.
Resumen
Las fórmulas racionales se pueden usar para resolver una variedad de problemas que involucran tarifas, tiempos y trabajo. Las ecuaciones de variación directa, inversa y conjunta son ejemplos de fórmulas racionales. En variación directa, las variables tienen una relación directa: a medida que una cantidad aumenta, la otra cantidad también aumentará. A medida que una cantidad disminuye, la otra cantidad disminuye. En variación inversa, las variables tienen una relación inversa: a medida que una variable aumenta, la otra disminuye, y viceversa. La variación conjunta es lo mismo que la variación directa excepto que hay dos o más variables.


