16.3.1: Resolver ecuaciones radicales

Última actualización
Guardar como PDF

Page ID: 111275

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Resuelve ecuaciones que contienen radicales.
Reconocer soluciones extrañas.
Resolver problemas de aplicación que involucren ecuaciones radicales como parte de la solución.

Introducción

Una ecuación que contiene una expresión radical se denomina ecuación radical. Resolver ecuaciones radicales requiere aplicar las reglas de los exponentes y seguir algunos principios algebraicos básicos. En algunos casos, también requiere estar atento a los errores generados al elevar cantidades desconocidas a una potencia pareja.

Cuadrando ambos lados

Una estrategia básica para resolver ecuaciones radicales es aislar primero el término radical, y luego elevar ambos lados de la ecuación a un poder para eliminar el radical. (El motivo del uso de los poderes quedará claro en un momento.) Este es el mismo tipo de estrategia que utilizó para resolver otras ecuaciones no radicales: reorganizar la expresión para aislar la variable que desea conocer, y luego resolver la ecuación resultante.

Hay dos ideas clave que vas a utilizar para resolver ecuaciones radicales. El primero es que si$\ a=b$, entonces$\ a^{2}=b^{2}$. (Esta propiedad le permite cuadrar ambos lados de una ecuación y estar seguro de que los dos lados siguen siendo iguales). El segundo es que si la raíz cuadrada de cualquier número no negativo$\ x$ es cuadrada, entonces obtienes$\ x$:$\ (\sqrt{x})^{2}=x$. (Esta propiedad le permite “eliminar” los radicales de sus ecuaciones.)

Empecemos con una ecuación radical que puedes resolver en unos pocos pasos:$\ \sqrt{x}-3=5$.

Ejemplo

Resolver. $\ \sqrt{x}-3=5$

Solución

\ (\\ begin {array} {r} \ sqrt {x} -3&=5\\ +3&+3\ \ hline \ end {array}\)	Agrega 3 a ambos lados para aislar el término variable en el lado izquierdo de la ecuación.
$\ \sqrt{x}=8$	Recoger términos similares.
\ (\\ comenzar {alineado} (\ sqrt {x}) ^ {2} &=8^ {2}\\ x &=64 \ end {alineado}\)	Cuadrar ambos lados para eliminar el radical, ya que$\ (\sqrt{x})^{2}=x$. ¡Asegúrate de cuadrar los 8 también! Entonces simplifique.

$\ x=64$es la solución a$\ \sqrt{x}-3=5$.

Para verificar tu solución, puedes sustituir 64 in por$\ x$ en la ecuación original. ¿Lo hace$\ \sqrt{64}-3=5$? Sí, la raíz cuadrada de 64 es 8, y$\ 8-3=5$.

Observe cómo combinó términos similares y luego cuadró ambos lados de la ecuación en este problema. Este es un método estándar para eliminar un radical de una ecuación. Es importante aislar un radical en un lado de la ecuación y simplificar lo más posible antes de cuadrar. Cuantos menos términos haya antes de la cuadratura, menos términos adicionales se generarán por el proceso de cuadratura.

En el ejemplo anterior, sólo la variable$\ x$ estaba por debajo del radical. A veces necesitarás resolver una ecuación que contenga múltiples términos debajo de un radical. Sigue los mismos pasos para resolverlos, pero presta atención a un punto crítico: cuadrar ambos lados de una ecuación, no términos individuales. Observa cómo se resuelven los dos siguientes problemas.

Ejemplo

Resolver. $\ \sqrt{x+8}=3$

Solución

$\ (\sqrt{x+8})^{2}=(3)^{2}$	Observe cómo el radical contiene un binomio:$\ x+8$. Cuadra ambos lados para eliminar el radical.
\ (\\ comenzar {alineado} x+8 &=9\\ x &=1 \ end {alineado}\)	$\ (\sqrt{x+8})^{2}=x+8$. Ahora simplifique la ecuación y resuelva para$\ x$.
\ (\\ comenzar {alineado} \ sqrt {1+8} &=3\\ \ sqrt {9} &=3\\ 3 &=3 \ end {alineado}\)	Comprueba tu respuesta. Sustituir 1 por$\ x$ en la ecuación original produce una declaración verdadera, por lo que la solución es correcta.

$\ x=1$es la solución a$\ \sqrt{x+8}=3$.

Ejemplo

Resolver. $\ 1+\sqrt{2 x+3}=6$

Solución

\ (\\ begin {array} {r} 1+\ sqrt {2 x+3} -1=6-1\\ \ sqrt {2 x+3} =5\\ (\ sqrt {2 x+3}) ^ {2} =( 5) ^ {2} \ end {array}\)	Comience restando 1 de ambos lados para aislar el término radical. Después cuadrar ambos lados para eliminar el binomio del radical.
\ (\\ comenzar {alineado} 2 x+3 &=25\\ 2 x &=22\\ x &=11 \ final {alineado}\)	Simplifica la ecuación y resuelve para$\ x$.
\ (\\ begin {alineado} 1+\ sqrt {2 (11) +3} &=6\\ 1+\ sqrt {22+3} &=6\\ 1+\ sqrt {25} &=6\\ 1+5 &=6\\ 6 &=6 \ end {alineado}\)	Comprueba tu respuesta. Sustituir 11 por$\ x$ en la ecuación original produce una declaración verdadera, por lo que la solución es correcta.

$\ x=11$es la solución para$\ 1+\sqrt{2 x+3}=6$.

Resolviendo ecuaciones radicales

Sigue los cuatro pasos para resolver ecuaciones radicales.

Aislar la expresión radical.
Cuadrar ambos lados de la ecuación: Si$\ x=y$ entonces$\ x^{2}=y^{2}$.
Una vez eliminado el radical, resuelva por lo desconocido.
Consulta todas las respuestas.

Ejercicio

Resolver. $\ \sqrt{3 x+22}=4$

$\ x=2$
$\ x=\frac{16}{3}$
$\ x=-2$
$\ x=-6$

Responder

Incorrecto. Comprueba tu respuesta. Si sustitues$\ x=2$ en la ecuación, obtienes$\ \sqrt{3(2)+22}=4$, o$\ \sqrt{28}=4$. Esto no es correcto. Recuerda cuadrar ambos lados y luego resolver para$\ x$. La respuesta correcta es$\ x=-2$.
Incorrecto. Parece que cuadraste ambos lados pero ignoraste el$\ +22$ debajo del radical. Recuerda incluir todo el binomio cuando cuadras ambos lados; luego resuelve para$\ x$. La respuesta correcta es$\ x=-2$.
Correcto. Al cuadrar ambos lados, encuentras$\ (\sqrt{3 x+22})^{2}=(4)^{2}$ se vuelve$\ 3 x+22=16$, así$\ 3 x=-6$ y$\ x=-2$.
Incorrecto. Parece que solo cuadraste el lado izquierdo de la ecuación. Recuerda cuadrar ambos lados:$\ (\sqrt{3 x+22})^{2}=(4)^{2}$, que se convierte$\ 3 x+22=16$. Ahora resuelve para$\ x$. La respuesta correcta es$\ x=-2$.

Soluciones Extrañas

Seguir reglas es importante, pero también lo es prestar atención a las matemáticas que tienes delante, especialmente al resolver ecuaciones radicales. Eche un vistazo a este próximo problema que demuestra un potencial escollo de cuadrar ambos lados para eliminar al radical.

Ejemplo

Resolver. $\ \sqrt{a-5}=-2$

Solución

$\ (\sqrt{a-5})^{2}=(-2)^{2}$	Cuadrar ambos lados para quitar el término$\ a-5$ del radical.
\ (\\ begin {array} {r} a-5=4\\ a=9 \ end {array}\)	Escribe la ecuación simplificada, y resuelve para$\ a$.
\ (\\ comenzar {alineado} \ sqrt {9-5} &=-2\\ \ sqrt {4} &=-2\\ 2 &\ neq-2 \ final {alineado}\)	Ahora verifique la solución sustituyéndola$\ a=9$ en la ecuación original. t no comprueba!

Sin solución.

La respuesta$\ a=9$ no produce una declaración verdadera cuando se sustituye de nuevo en la ecuación original. ¿Qué pasó?

Consulta el problema original:$\ \sqrt{a-5}=-2$. Observe que el radical se establece igual a -2, y recuerde que la raíz cuadrada principal de un número sólo puede ser positiva. Esto significa que ningún valor para$\ a$ dará como resultado una expresión radical cuya raíz cuadrada positiva es -2! Te habrás dado cuenta de eso de inmediato y concluyeron que no había soluciones para$\ a$. Pero, ¿por qué el proceso de cuadratura creó una respuesta$\ a=9$,, que resultó ser incorrecta?

La respuesta está en el proceso de cuadrar a sí mismo. Cuando elevas un número a una potencia par, ya sea la segunda, cuarta o ^50ª potencia, puedes introducir una solución falsa porque el resultado de una potencia par es siempre un número positivo. Piénsalo:$\ 3^{2}$ y$\ (-3)^{2}$ son ambos 9, y$\ 2^{4}$ y$\ (-2)^{4}$ son ambos 16. Entonces cuando cuadraste -2 y obtuviste 4 en este problema, artificialmente volviste positiva la cantidad. Es por eso que aún pudiste encontrar un valor para$\ a$; ¡resolviste el problema como si estuvieras resolviendo$\ \sqrt{a-5}=2$! (La solución correcta$\ \sqrt{a-5}=-2$ es en realidad “ninguna solución”).

Los valores incorrectos de la variable, como los que se introducen como resultado del proceso de cuadratura, se denominan soluciones extrañas. Las soluciones extrañas pueden parecer la solución real, pero puedes identificarlas porque no crearán una declaración verdadera cuando se sustituyan de nuevo en la ecuación original. Esta es una de las razones por las que revisar tu trabajo es tan importante. Si no revisas tus respuestas sustituyéndolas de nuevo en la ecuación original, es posible que estés introduciendo soluciones extrañas en el problema.

Echa un vistazo al siguiente problema. Observe cómo es el problema original$\ x+4=\sqrt{x+10}$, pero después de que ambos lados están cuadrados, se vuelve$\ x^{2}+8 x+16=x+10$. Al cuadrar ambos lados puede haber introducido una solución extraña.

Ejemplo

Resolver. $\ x+4=\sqrt{x+10}$

Solución

$\ (x+4)^{2}=(\sqrt{x+10})^{2}$	Cuadrar ambos lados para quitar el término$\ x+10$ del radical.
\ (\\ comenzar {alineado} (x+4) (x+4) &=x+10\\ x^ {2} +8 x+16 &=x+10\ x^ {2} +8 x-x+16-10 &=0\\ x^ {2} +7 x+6 &=0\\ (x+6) (x+1) &=0 \\ end { alineado}\)	Ahora simplifica y resuelve la ecuación. Combina términos similares, y luego factor.
\ (\\ begin {array} {r} (x+6) =0 &\ quad\ text {o}\ quad & (x+1) =0\\ x=-6 &\ quad\ text {o}\ quad& x=-1 \ end {array}\)	Establezca cada factor igual a cero y resuelva para$\ x$.
\ (\\ begin {array} {cc} -6+4=\ sqrt {-6+10} & -1+4=\ sqrt {-1+10}\ -2=\ sqrt {4} & 3=\ sqrt {9}\\ -2=2 & 3=3\\ \ text {FALSO! } &\ text {¡VERDADERO! } \ end {array}\)	Ahora comprueba ambas soluciones sustituyéndolas en la ecuación original. Ya que$\ x=-6$ produce una declaración falsa, es una solución extraña.

$\ x=-1$es la única solución

Puede ser difícil entender por qué existen soluciones extrañas en absoluto. Pensar en soluciones extrañas al graficar la ecuación puede ayudarte a dar sentido a lo que está sucediendo.

Se puede graficar$\ x+4=\sqrt{x+10}$ en un plano de coordenadas dividiéndolo en un sistema de dos ecuaciones:$\ y=x+4$ y$\ y=\sqrt{x+10}$. A continuación se muestra la gráfica. Observe cómo las dos gráficas se cruzan en un punto, cuando el valor de$\ x$ es -1. Este es el valor de$\ x$ que satisface ambas ecuaciones, por lo que es la solución al sistema.

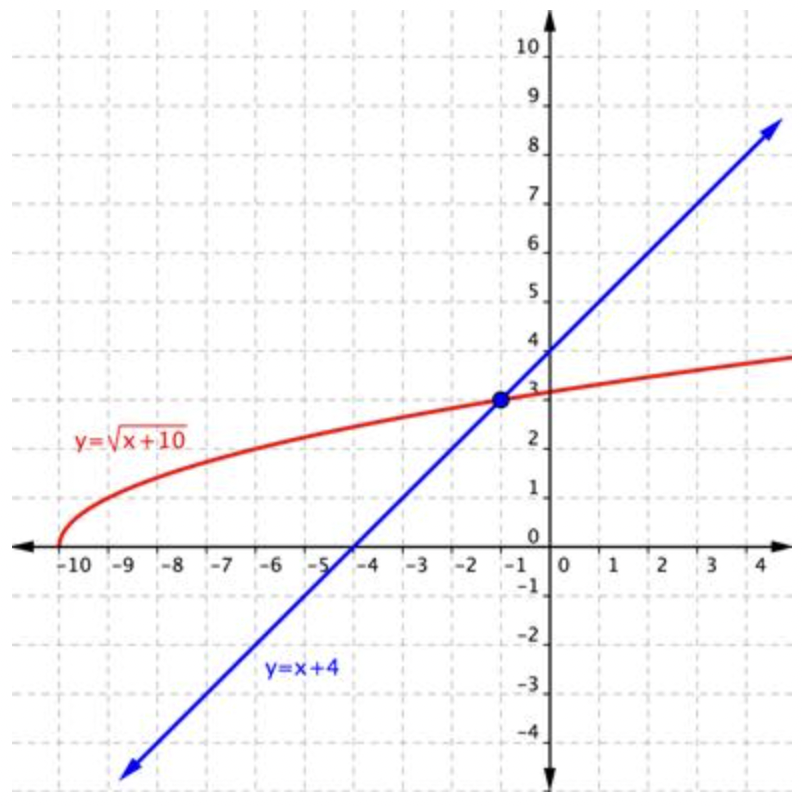
$Screen Shot 2021-07-13 a las 4.41.28 PM.png$

Ahora, siguiendo el trabajo que hicimos en el problema del ejemplo, cuadremos ambas expresiones para eliminar la variable del radical. En lugar de resolver la ecuación ahora$\ x+4=\sqrt{x+10}$ estamos resolviendo la ecuación$\ (x+4)^{2}=(\sqrt{x+10})^{2}$, o$\ x^{2}+8 x+16=x+10$. Las gráficas de$\ y=x^{2}+8 x+16$ y$\ y=x+10$ se trazan a continuación. Observe cómo las dos gráficas se cruzan en dos puntos, cuando los valores de$\ x$ son -1 y -6.

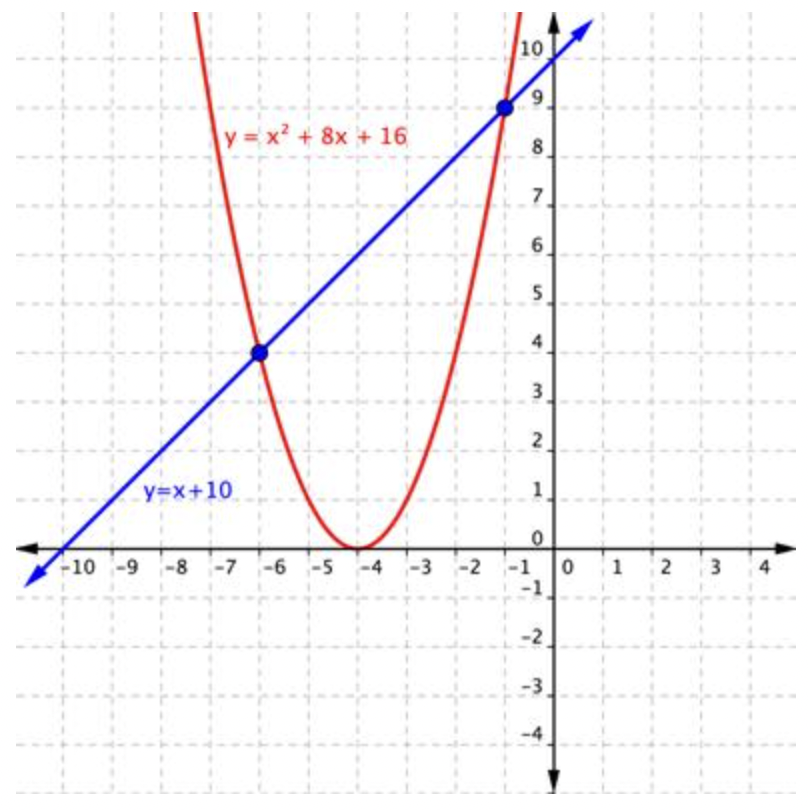
$Screen Shot 2021-07-13 a las 4.50.29 PM.png$

Si bien$\ x=-1$ se muestra como una solución en ambas gráficas, la cuadratura de ambos lados de la ecuación tuvo el efecto de agregar una solución extraña,$\ x=-6$. Nuevamente, ¡por eso es tan importante verificar tus respuestas a la hora de resolver ecuaciones radicales!

Ejemplo

Resolver. $\ 4+\sqrt{x+2}=x$

Solución

$\ \sqrt{x+2}=x-4$	Aislar el término radical.
$\ (\sqrt{x+2})^{2}=(x-4)^{2}$	Cuadrar ambos lados para quitar el término$\ x+2$ del radical.
\ (\\ comenzar {alineado} x+2 &=x^ {2} -8 x+16\\ 0 &=x^ {2} -8 x-x+16-2\\ 0 &=x^ {2} -9 x+14\\ 0 & =( x-7) (x-2) \ end {alineado}\)	Ahora simplifica y resuelve la ecuación. Combina términos similares, y luego factor.
\ (\\ begin {array} {r} (x-7) =0 &\ text {o} & (x-2) =0\\ x=7 &\ text {o} & x=2 \ end {array}\)	Establezca cada factor igual a cero y resuelva para$\ x$.
\ (\\ begin {array} {rr} 4+\ sqrt {7+2} =7 &\ quad 4+\ sqrt {2+2} =2\\ 4+\ sqrt {9} =7 y 4+\ sqrt {4} =2\\ 4+3=7 & 4+2 = 2\ 7=7 y 6=2\ \ text {VERDADERO!} &\ text {FALSO!} \ end {array}\)	Ahora comprueba ambas soluciones sustituyéndolas en la ecuación original. Ya que$\ x=2$ produce una declaración falsa, es una solución extraña.

$\ x=7$es la única solución.

Ejercicio

Resolver. $\ x-3=\sqrt{4 x+9}$

$\ x=3,0$
$\ x=0,10$
$\ x=0$
$\ x=10$

Responder

Incorrecto. Para resolver la ecuación, cuadrar ambos lados y luego resolver la ecuación resultante$\ x^{2}-6 x+9=4 x+9$. La respuesta correcta es:$\ x=10$.
Incorrecto. Resolviste la ecuación$\ x^{2}-6 x+9=4 x+9$ correctamente, pero olvidaste evaluar ambos valores para$\ x$ en la ecuación original. $\ x=0$es una solución extraña ya que no hace que la ecuación original sea cierta! La respuesta correcta es:$\ x=10$
Incorrecto. Cuando cuadras ambos lados y luego resuelves la ecuación resultante$\ x^{2}-6 x+9=4 x+9$,, obtienes$\ x=0$ como una posible solución. Sin embargo, ¡$\ x=0$es una solución extraña ya que no hace que la ecuación original sea cierta! La respuesta correcta es:$\ x=10$
Correcto. Resolviendo la ecuación, encuentras que al cuadrar ambos lados resulta en$\ x^{2}-6 x+9=4 x+9$, lo que simplifica a$\ x^{2}-10 x=0$. Aunque esta ecuación produce$\ x$ valores de 0 o 10, 0 es extraño ya que no hace que la ecuación original sea verdadera.

Resolución de problemas de aplicación con ecuaciones radicales

Las ecuaciones radicales juegan un papel importante en la ciencia, la ingeniería e incluso la música. En ocasiones es posible que necesites usar lo que sabes sobre ecuaciones radicales para resolver diferentes variables en este tipo de problemas.

Ejemplo

Una forma de medir la cantidad de energía que posee un objeto en movimiento (como un automóvil) es encontrando su Energía Cinética. La Energía Cinética ($\ E_{k}$, medida en Julios) de un objeto depende de la masa del objeto ($\ m$, medida en kg) y la velocidad ($\ v$, medida en metros por segundo) y puede escribirse como$\ v=\sqrt{\frac{2 E_{k}}{m}}$.

¿Cuál es la Energía Cinética de un objeto con una masa de 1,000 kilogramos que viaja a 30 metros por segundo?

Solución

\ (\\ begin {array} {r} E_ {k} =\ text {desconocido}\\ m=1000\\ v=30 \ end {array}\)	Identificar variables y valores conocidos.
$\ 30=\sqrt{\frac{2 E_{k}}{1,000}}$	Sustituir valores en la fórmula.
\ (\\ begin {alineado} (30) ^ {2} &=\ izquierda (\ frac {\ sqrt {2 E_ {k}}} {1,000}\ derecha) ^ {2}\\ 900 &=\ frac {2 E_ {k}} {1,000}\ 900\ cdot 1,000 &=\ frac {2 E_ {k}} {1,000}\ cdot 1,000\ 900.000 &=2 E_ {k}\\ \ frac {900,000} {2} &=\ frac {2 E_ {k}} {2}\\ 450,000 &=E_ {k} \ end {alineado}\)	Resuelve la ecuación radical para$\ E_{k}$.
\ (\\ begin {array} {l} 30=\ sqrt {\ frac {2\ cdot 450.000} {1,000}}\\ 30=\ sqrt {\ frac {900,000} {1,000}}\\ 30=\ sqrt {900}\\ 30=30 \ end {array}\)	Ahora comprueba la solución sustituyéndola en la ecuación original.

La Energía Cinética es de 450,000 Julios.

Resumen

Un método común para resolver ecuaciones radicales es elevar ambos lados de una ecuación a cualquier poder que elimine el signo radical de la ecuación. Pero ten cuidado: cuando ambos lados de una ecuación se elevan a una potencia pareja, existe la posibilidad de que se introduzcan soluciones extrañas. Al resolver una ecuación radical, es importante verificar siempre su respuesta sustituyendo el valor en la ecuación original. Si obtienes una declaración verdadera, entonces ese valor es una solución; si obtienes una declaración falsa, entonces ese valor no es una solución.

\(\ (\sqrt{x+8})^{2}=(3)^{2}\)	Observe cómo el radical contiene un binomio:\(\ x+8\). Cuadra ambos lados para eliminar el radical.
\ (\\ comenzar {alineado} x+8 &=9\\ x &=1 \ end {alineado}\)	\(\ (\sqrt{x+8})^{2}=x+8\). Ahora simplifique la ecuación y resuelva para\(\ x\).
\ (\\ comenzar {alineado} \ sqrt {1+8} &=3\\ \ sqrt {9} &=3\\ 3 &=3 \ end {alineado}\)	Comprueba tu respuesta. Sustituir 1 por\(\ x\) en la ecuación original produce una declaración verdadera, por lo que la solución es correcta.

\(\ (\sqrt{a-5})^{2}=(-2)^{2}\)	Cuadrar ambos lados para quitar el término\(\ a-5\) del radical.
\ (\\ begin {array} {r} a-5=4\\ a=9 \ end {array}\)	Escribe la ecuación simplificada, y resuelve para\(\ a\).
\ (\\ comenzar {alineado} \ sqrt {9-5} &=-2\\ \ sqrt {4} &=-2\\ 2 &\ neq-2 \ final {alineado}\)	Ahora verifique la solución sustituyéndola\(\ a=9\) en la ecuación original. t no comprueba!

\ (\\ begin {array} {r} \ sqrt {x} -3&=5\\ +3&+3\ \ hline \ end {array}\)	Agrega 3 a ambos lados para aislar el término variable en el lado izquierdo de la ecuación.
\(\ \sqrt{x}=8\)	Recoger términos similares.
\ (\\ comenzar {alineado} (\ sqrt {x}) ^ {2} &=8^ {2}\\ x &=64 \ end {alineado}\)	Cuadrar ambos lados para eliminar el radical, ya que\(\ (\sqrt{x})^{2}=x\). ¡Asegúrate de cuadrar los 8 también! Entonces simplifique.

\(\ (x+4)^{2}=(\sqrt{x+10})^{2}\)	Cuadrar ambos lados para quitar el término\(\ x+10\) del radical.
\ (\\ comenzar {alineado} (x+4) (x+4) &=x+10\\ x^ {2} +8 x+16 &=x+10\ x^ {2} +8 x-x+16-10 &=0\\ x^ {2} +7 x+6 &=0\\ (x+6) (x+1) &=0 \\ end { alineado}\)	Ahora simplifica y resuelve la ecuación. Combina términos similares, y luego factor.
\ (\\ begin {array} {r} (x+6) =0 &\ quad\ text {o}\ quad & (x+1) =0\\ x=-6 &\ quad\ text {o}\ quad& x=-1 \ end {array}\)	Establezca cada factor igual a cero y resuelva para\(\ x\).
\ (\\ begin {array} {cc} -6+4=\ sqrt {-6+10} & -1+4=\ sqrt {-1+10}\ -2=\ sqrt {4} & 3=\ sqrt {9}\\ -2=2 & 3=3\\ \ text {FALSO! } &\ text {¡VERDADERO! } \ end {array}\)	Ahora comprueba ambas soluciones sustituyéndolas en la ecuación original. Ya que\(\ x=-6\) produce una declaración falsa, es una solución extraña.

\(\ \sqrt{x+2}=x-4\)	Aislar el término radical.
\(\ (\sqrt{x+2})^{2}=(x-4)^{2}\)	Cuadrar ambos lados para quitar el término\(\ x+2\) del radical.
\ (\\ comenzar {alineado} x+2 &=x^ {2} -8 x+16\\ 0 &=x^ {2} -8 x-x+16-2\\ 0 &=x^ {2} -9 x+14\\ 0 & =( x-7) (x-2) \ end {alineado}\)	Ahora simplifica y resuelve la ecuación. Combina términos similares, y luego factor.
\ (\\ begin {array} {r} (x-7) =0 &\ text {o} & (x-2) =0\\ x=7 &\ text {o} & x=2 \ end {array}\)	Establezca cada factor igual a cero y resuelva para\(\ x\).
\ (\\ begin {array} {rr} 4+\ sqrt {7+2} =7 &\ quad 4+\ sqrt {2+2} =2\\ 4+\ sqrt {9} =7 y 4+\ sqrt {4} =2\\ 4+3=7 & 4+2 = 2\ 7=7 y 6=2\ \ text {VERDADERO!} &\ text {FALSO!} \ end {array}\)	Ahora comprueba ambas soluciones sustituyéndolas en la ecuación original. Ya que\(\ x=2\) produce una declaración falsa, es una solución extraña.

\ (\\ begin {array} {r} E_ {k} =\ text {desconocido}\\ m=1000\\ v=30 \ end {array}\)	Identificar variables y valores conocidos.
\(\ 30=\sqrt{\frac{2 E_{k}}{1,000}}\)	Sustituir valores en la fórmula.
\ (\\ begin {alineado} (30) ^ {2} &=\ izquierda (\ frac {\ sqrt {2 E_ {k}}} {1,000}\ derecha) ^ {2}\\ 900 &=\ frac {2 E_ {k}} {1,000}\ 900\ cdot 1,000 &=\ frac {2 E_ {k}} {1,000}\ cdot 1,000\ 900.000 &=2 E_ {k}\\ \ frac {900,000} {2} &=\ frac {2 E_ {k}} {2}\\ 450,000 &=E_ {k} \ end {alineado}\)	Resuelve la ecuación radical para\(\ E_{k}\).
\ (\\ begin {array} {l} 30=\ sqrt {\ frac {2\ cdot 450.000} {1,000}}\\ 30=\ sqrt {\ frac {900,000} {1,000}}\\ 30=\ sqrt {900}\\ 30=30 \ end {array}\)	Ahora comprueba la solución sustituyéndola en la ecuación original.