17.1.1: Identificar funciones
- Page ID
- 111254
- Determinar si una relación es una función.
- Determinar el dominio de una función y el rango de una función.
- Determine si una gráfica es la de una función mediante una prueba de línea vertical.
Introducción
El álgebra nos da una forma de explorar y describir las relaciones. Imagina lanzar una pelota hacia arriba en el aire y verla subir para llegar a su punto más alto antes de volver a caer en tus manos. A medida que pasa el tiempo, la altura de la pelota cambia. Existe una relación entre la cantidad de tiempo que ha transcurrido desde el lanzamiento y la altura de la pelota. En matemáticas, una correspondencia entre variables que cambian juntas (como el tiempo y la altura) se llama relación. Algunas, pero no todas, las relaciones también pueden describirse como funciones.
Definición de la función
Hay muchos tipos de relaciones. Las relaciones son simplemente correspondencias entre conjuntos de valores o información. Piensa en los miembros de tu familia y sus edades. El emparejamiento de cada miembro de tu familia y su edad es una relación. Cada miembro de la familia se puede emparejar con una edad en el conjunto de edades de los miembros de su familia. Otro ejemplo de relación es el emparejamiento de un estado con sus senadores de Estados Unidos. Cada estado puede ser emparejado con dos individuos que han sido electos para fungir como senador. A su vez, cada senador puede ser emparejado con un estado específico que él o ella representa. Ambos son ejemplos de relaciones de la vida real.
El primer valor de una relación es un valor de entrada y el segundo valor es el valor de salida. Una función es un tipo específico de relación en la que cada valor de entrada tiene uno y solo un valor de salida. Una entrada es el valor independiente, y el valor de salida es el valor dependiente, ya que depende del valor de la entrada.
Observe en la primera tabla a continuación, donde la entrada es “nombre” y la salida es “edad”, cada entrada coincide con exactamente una salida. Este es un ejemplo de una función.
|
(Entrada) Nombre del miembro de la familia |
(Salida) Edad del miembro de la familia |
| Nellie | 13 |
| Marcos | 11 |
| Esther | 46 |
| Samuel | 47 |
| Nina | 47 |
| Paul | 47 |
| Katrina | 21 |
| Andrew | 16 |
| María | 13 |
| Ana | 81 |
Compare esto con la siguiente tabla, donde la entrada es “age” y la salida es “name”. Algunas de las entradas dan como resultado más de una salida. Este es un ejemplo de una correspondencia que no es una función.
| Información inicial (entrada): Edad del miembro de la familia | Información Relacionada (Salida): Nombre del Miembro de la Familia |
| 11 | Marcos |
| 13 |
Nellie María |
| 16 | Andrew |
| 21 | Katrina |
| 46 | Esther |
| 47 |
Samuel Nina Paul |
| 81 | Ana |
Revisemos nuestros ejemplos para determinar si las relaciones son funciones o no y bajo qué circunstancias. Recuerda que una relación es una función si solo hay una salida por cada entrada.
| Entrada | Salida | ¿Función? | ¿Por qué o por qué no? |
| Nombre del senador | Nombre del Estado | Sí | Por cada entrada, sólo habrá una salida porque un senador sólo representa un estado. |
| Nombre del Estado | Nombre del senador | No | Por cada estado que sea una entrada, resultarían 2 nombres de senadores porque cada estado tiene dos senadores. |
| Tiempo transcurrido | Altura de una bola lanzada | Sí | En un momento específico, la pelota tiene una altura específica. |
| Altura de una bola lanzada | Tiempo transcurrido | No | Recuerden que la pelota fue arrojada hacia arriba y cayó al suelo. Entonces, para una altura dada, podría haber dos momentos diferentes cuando el balón estaba a esa altura. La altura de entrada puede dar como resultado más de una salida. |
| Número de autos | Número de llantas | Sí | Para cualquier entrada de un número específico de autos, hay una salida específica que representa el número de llantas. |
| Número de llantas | Número de autos | Sí | Para cualquier entrada de un número específico de llantas, hay una salida específica que representa el número de autos. |
¿Cuál de las siguientes situaciones describe una función?
- Tu edad y tu peso al mediodía de tu cumpleaños cada año.
- El número de personas en un equipo profesional de béisbol y el nombre del equipo.
- El diámetro de una galleta y el número de chispas de chocolate que contiene.
- Contestar
-
- Correcto. La edad solo aumenta mientras que el peso puede cambiar. En cada cumpleaños, solo tienes un peso al mediodía, así que por cada entrada, solo hay una salida.
- Incorrecto. Todos los equipos profesionales de béisbol tienen el mismo número de jugadores, por lo que el número de jugadores no es una función del nombre del equipo. La respuesta correcta es tu edad y tu peso al mediodía de tu cumpleaños cada año.
- Incorrecto. Aunque las galletas más grandes pueden contener más chips, el número exacto en cualquier tamaño de galleta variará con la receta y con qué tan uniforme se mezcla y distribuye la masa. Una sola entrada de tamaño de cookie producirá diferentes salidas de chips. La respuesta correcta es tu edad y tu peso al mediodía de tu cumpleaños cada año.
Las relaciones se pueden escribir como pares ordenados de números o como números en una tabla de valores. Al examinar las entradas (coordenadas x) y salidas (coordenadas y), se puede determinar si la relación es o no una función. Recuerda, en una función cada entrada tiene solo una salida. Siguen un par de ejemplos.
¿La relación dada por el conjunto de pares ordenados por debajo de una función?
\(\ \{(-3,-6),(-2,-1),(1,0),(1,5),(2,0)\}\)
Solución
|
Organizar los pares ordenados en una mesa puede ayudar. Por definición, las entradas en una función tienen solo una salida. La entrada 1 tiene dos salidas: 0 y 5. |
La relación no es una función.
¿La relación dada por el conjunto de pares ordenados por debajo de una función?
\(\ \{(-3,4),(-2,4),(-1,4),(2,4),(3,4)\}\)
Solución
|
Se podría reorganizar la información mediante la creación de una tabla. Cada entrada tiene solo una salida, y el hecho de que sea la misma salida (4) no importa. |
Esta relación es una función.
Recuerda que en una función, el valor de entrada debe tener uno y solo un valor para la salida.
Dominio y Rango
Hay un nombre para el conjunto de valores de entrada y otro nombre para el conjunto de valores de salida para una función. El conjunto de valores de entrada se llama el dominio de la función. Y el conjunto de valores de salida se llama el rango de la función.
Si tienes un conjunto de pares ordenados, puedes encontrar el dominio enumerando todos los valores de entrada, que son las coordenadas x. Y para encontrar el rango, enumere todos los valores de salida, que son las coordenadas y.
Entonces, para el siguiente conjunto de pares ordenados,
\(\ \{(-2,0),(0,6),(2,12),(4,18)\}\)
Tienes lo siguiente:
Dominio:\(\ \{-2,0,2,4\}\)
Rango:\(\ \{0,6,12,18\}\)
Jamie planea vender pasteles caseros por $10 cada uno en un puesto de granja local. La cantidad de dinero que hace es función de cuántas tartas vende: $0 si vende 0 pasteles, $10 si vende 1 pastel, $20 si vende 2 pasteles, y así sucesivamente. No quiere que los pasteles se echen a perder antes de poder venderlos, por lo que no hará (ni venderá) más de 9 tartas. ¿Cuál es el dominio y el rango para esa función?
- Dominio:\(\ \{0,10,20,30,40,50,60,70,80,90\}\) Rango:\(\ \{0,1,2,3,4,5,6,7,8,9\}\)
- Dominio:\(\ \{0,1,2,3,4,5,6,7,8,9\}\) Rango:\(\ \{0,10,20,30,40,50,60,70,80,90\}\)
- Dominio:\(\ \{0,1,2\}\) Rango:\(\ \{0,10,20\}\)
- Dominio: todos los números mayores o iguales a 0
- Contestar
-
- Incorrecto. El número de tartas es la entrada, y la cantidad de dinero es la salida de la función. Eso significa que el dominio es todo el número posible de pasteles, y el rango es todo el dinero posible hecho de esos pasteles. La respuesta correcta es Dominio:\(\ \{0,1,2,3,4,5,6,7,8,9\}\) Rango:\(\ \{0,10,20,30,40,50,60,70,80,90\}\)
- Correcto. El número de tartas que Jamie puede vender es el insumo, y ese puede ser cualquier número entero desde 0 hasta el máximo que haría, 9. El dinero que obtiene de esos pasteles es siempre un múltiplo de 10:0 por 0 pasteles, 10 por 1 pastel, 20 por 2 pasteles, y así sucesivamente.
- Incorrecto. Tanto el dominio como el rango continúan más allá de esos valores. Jamie puede vender hasta 9 pasteles, y como resultado puede ganar más de $20. Debe incluir todos los valores posibles del dominio y rango. La respuesta correcta es Dominio:\(\ \{0,1,2,3,4,5,6,7,8,9\}\) Rango:\(\ \{0,10,20,30,40,50,60,70,80,90\}\).
- Incorrecto. Jamie no vende fracciones de tartas, por lo que las únicas entradas posibles son números enteros del 0 al 9, y las únicas salidas posibles son 0 y múltiplos de 10 hasta 90. La respuesta correcta es Dominio:\(\ \{0,1,2,3,4,5,6,7,8,9\}\) Rango:\(\ \{0,10,20,30,40,50,60,70,80,90\}\).
Declarar el dominio y el rango de la siguiente función. \(\ \{(-3,5),(-2,5),(-1,5),(0,5),(1,5),(2,5)\}\)
Solución
| \(\ \{-3,-2,-1,0,1,2\}\) | El dominio es todas las coordenadas x. |
| \(\ \{5\}\) | El rango es todas las coordenadas y. Cada par ordenado tiene la misma coordenada y. Solo necesita ser listado una vez. |
Dominio:\(\ \{-3,-2,-1,0,1,2\}\)
Rango:\(\ \{5\}\)
Encuentra el dominio y el rango para la función.
| x | y |
| -5 | -6 |
| -2 | -1 |
| -1 | 0 |
| 0 | 3 |
| 5 | 15 |
Solución
| \(\ \{-5,-2,-1,0,5\}\) | El dominio es el conjunto de entradas o coordenadas x. |
| \(\ \{-6,-1,0,3,15\}\) | El rango es el conjunto de salidas de coordenadas y. |
Dominio:\(\ \{-5,-2,-1,0,5\}\)
Rango:\(\ \{-6,-1,0,3,15\}\)
Uso de la Prueba de Línea Vertical
Cuando tanto la cantidad independiente (entrada) como la cantidad dependiente (salida) son números reales, una función puede ser representada por una gráfica en el plano de coordenadas. El valor independiente se traza en el eje x y el valor dependiente se traza en el eje. El hecho de que cada valor de entrada tenga exactamente un valor de salida significa que las gráficas de funciones tienen ciertas características. Para cada entrada en la gráfica, habrá exactamente una salida.
Por ejemplo, la gráfica de la siguiente función dibujada en azul parece un semicírculo. Sabes que\(\ y\) es una función de\(\ x\) porque para cada coordenada x hay exactamente una coordenada y.
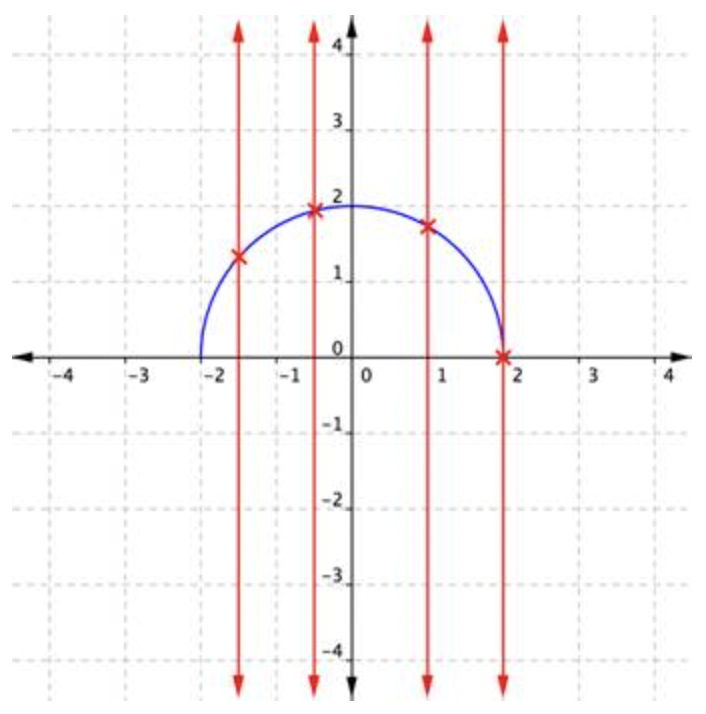
Si dibuja una línea vertical a través de la gráfica de la función, solo se cruza con la función una vez por cada valor de\(\ x\). Eso es cierto sin importar dónde se dibuje la línea vertical. Colocar o deslizar dicha línea a través de una gráfica es una buena manera de determinar si muestra una función.
Compara la gráfica anterior con esta, que parece un círculo azul. Esta relación no puede ser una función, porque algunas de las coordenadas x tienen dos coordenadas y correspondientes.
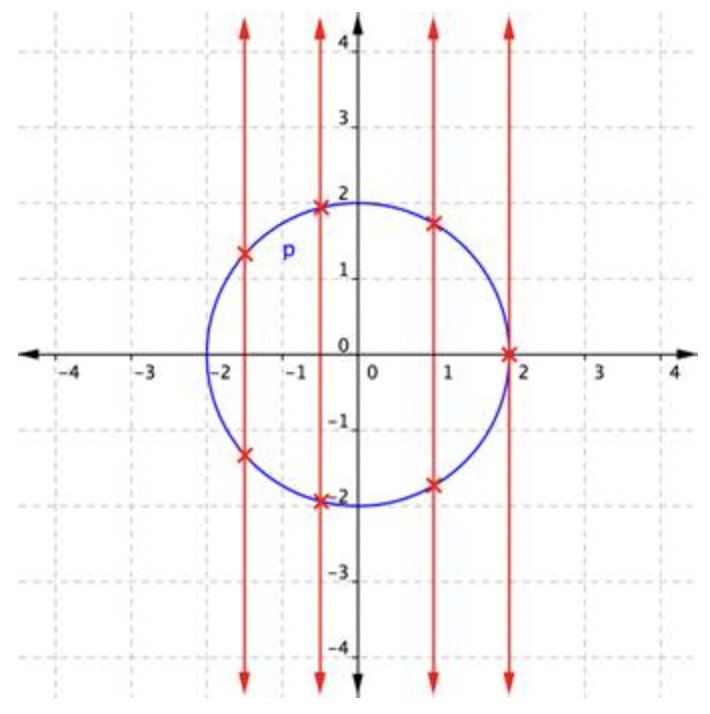
Cuando se coloca una línea vertical a través de la gráfica de esta relación, se cruza con la gráfica más de una vez para algunos valores de x. Si una gráfica muestra dos o más intersecciones con una línea vertical, entonces una entrada (coordenada x) puede tener más de una salida (coordenada y), e y no es una función de x. Examinando el gráfico de una relación para determinar si una línea vertical se cruzaría con más de un punto es una forma rápida de determinar si la relación que muestra la gráfica es una función. Este método a menudo se llama la “prueba de línea vertical”.
El método de línea vertical también se puede aplicar a un conjunto de pares ordenados trazados en un plano de coordenadas para determinar si la relación es una función. Considera los pares ordenados\(\ \{(-1,3),(-2,5),(-3,3),(-5,-3)\}\), trazados en la gráfica de abajo.
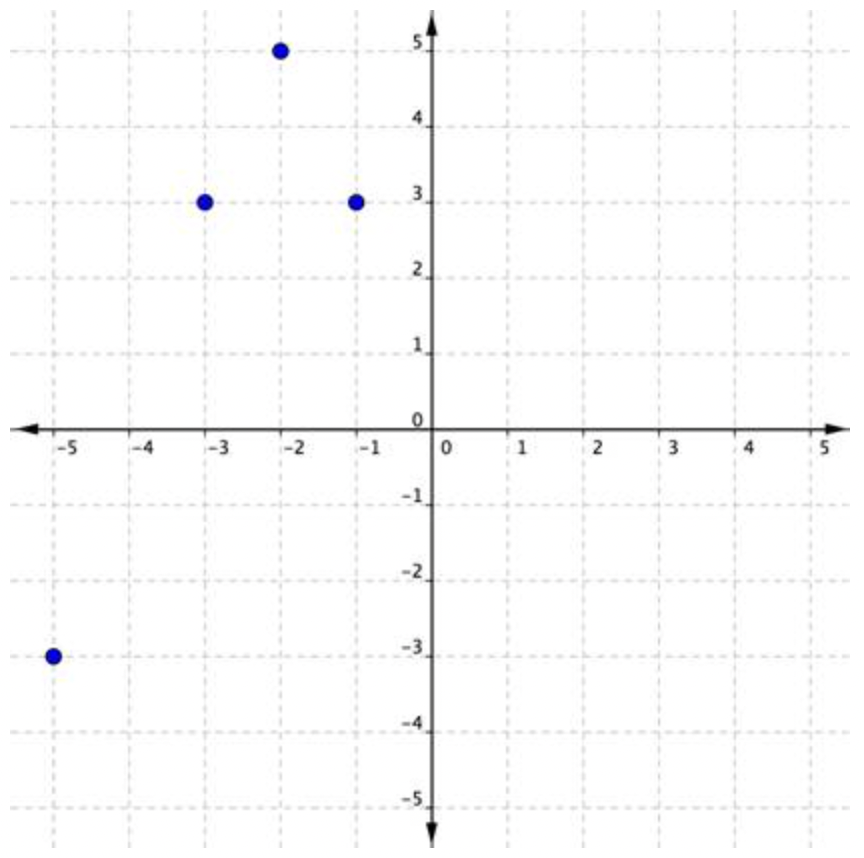
Aquí, puedes ver que en el conjunto de pares que acabamos de enumerar, cada valor independiente tiene uno y solo un valor dependiente. También puede verificar que una línea vertical que recorre cualquier punto no se intersecaría con otro punto. Una línea horizontal cruzaría dos de los puntos, pero eso está bien. (Recuerda, ¡es una prueba de línea vertical, no una prueba de línea horizontal que determina si una relación es una función!)
En otro conjunto de pares ordenados,\(\ \{(3,-1),(5,-2),(3,-3),(-3,5)\}\), una de las entradas, 3, puede producir dos salidas diferentes, -1 y -3. Ya sabes lo que eso significa: este conjunto de pares ordenados no es una función. Una trama lo confirma.
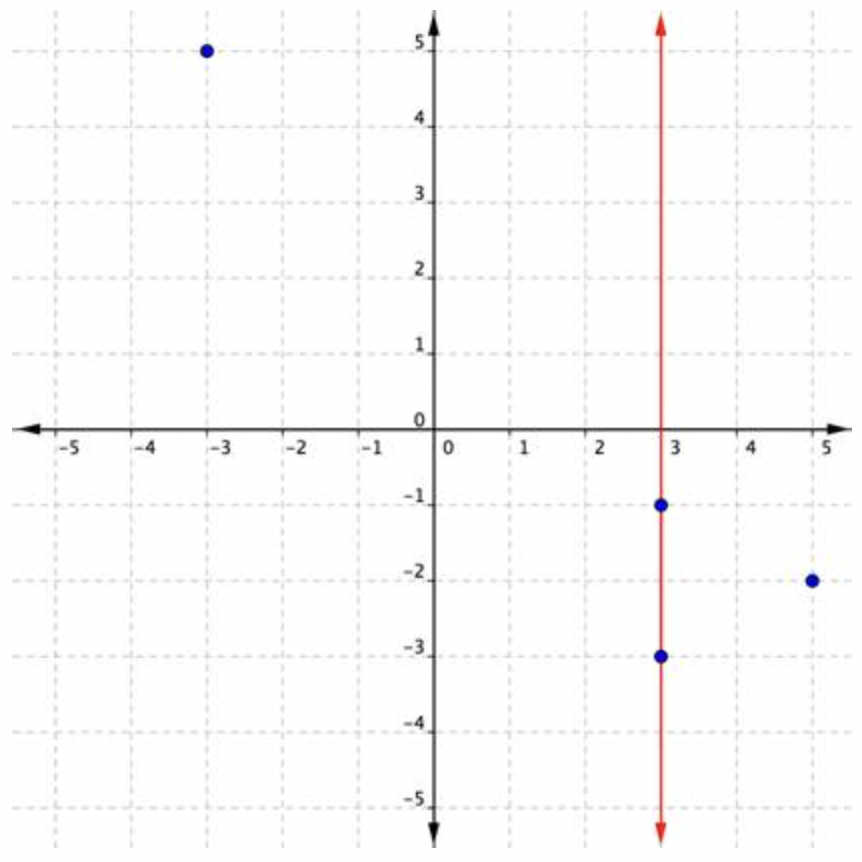
Observe que una línea vertical pasa por dos puntos trazados. Una coordenada x tiene múltiples coordenadas y. Esta relación no es una función.
¿Cuál de los siguientes es un conjunto de pares ordenados que representan una función?
- \(\ \{2,4,4,8,8,16,16,32\}\)
- \(\ \{(0,0),(1,1),(1,-1),(2,2),(2,-2)\}\)
- \(\ \{(5,-10),(5,-3),(5,0),(5,2),(5,17)\}\)
- \(\ \{(-2,2),(-1,1),(0,0),(1,1),(2,2)\}\)
- Contestar
-
- Incorrecto. Estos números no se agrupan en pares ordenados. Sin una notación adecuada, es imposible saber qué valores son las entradas y cuáles son las salidas. La respuesta correcta es\(\ \{(-2,2),(-1,1),(0,0),(1,1),(2,2)\}\).
- Incorrecto. Algunas coordenadas x se repiten y tienen diferentes coordenadas y. Esto no es una función. La respuesta correcta es\(\ \{(-2,2),(-1,1),(0,0),(1,1),(2,2)\}\).
- Incorrecto. Este conjunto contiene cinco pares ordenados, cada uno con una coordenada x de 5 y diferentes coordenadas y como salidas. Esto no es una función, ya que una función requiere que cada entrada tenga solo una salida. La respuesta correcta es\(\ \{(-2,2),(-1,1),(0,0),(1,1),(2,2)\}\).
- Correcto. No se repite ninguna coordenada x y cada una tiene exactamente una coordenada y, por lo tanto,\(\ \{(-2,2),(-1,1),(0,0),(1,1),(2,2)\}\) es una función.
Resumen
En la vida real y en Álgebra, muchas veces se vinculan diferentes variables. Cuando un cambio en el valor de una variable provoca un cambio en el valor de otra variable, su interacción se denomina relación. Una relación tiene un valor de entrada que corresponde a un valor de salida. Cuando cada valor de entrada tiene uno y solo un valor de salida, esa relación es una función. Las funciones se pueden escribir como pares ordenados, tablas o gráficos. El conjunto de valores de entrada se llama dominio, y el conjunto de valores de salida se llama rango.


