18.1.1: Introducción a las Funciones Exponenciales
- Page ID
- 111454
- Graficar ecuaciones exponenciales y funciones.
- Resolver problemas aplicados utilizando problemas exponenciales y sus gráficas.
Introducción
Además de las funciones lineales, cuadráticas, racionales y radicales, existen funciones exponenciales. Las funciones exponenciales tienen la forma\(f(x)=b^{x}\), dónde\(b > 0\) y\(b \neq 1\). Al igual que en cualquier expresión exponencial,\(b\) se llama la base y\(x\) se llama el exponente.
Un ejemplo de una función exponencial es el crecimiento de bacterias. Algunas bacterias se duplican cada hora. Si comienzas con 1 bacteria y se duplica cada hora, tendrás\(2^x\) bacterias después de\(x\) horas. Esto se puede escribir como\(f(x) = 2^x\).
Antes de comenzar,\(f(0)=2^{0}=1\)
Después de 1 hora,\(f(1)=2^{1}=2\)
En 2 horas,\(f(2)=2^{2}=4\)
En 3 horas,\(f(3)=2^{3}=8\)
y así sucesivamente.
Con la definición\(f(x)=b^{x}\) y las restricciones que\(b > 0\) y eso (b\ neq 1\), el dominio de una función exponencial es el conjunto de todos los números reales. El rango es el conjunto de todos los números reales positivos. En la siguiente gráfica se muestra\(f(x) = 2^x\).
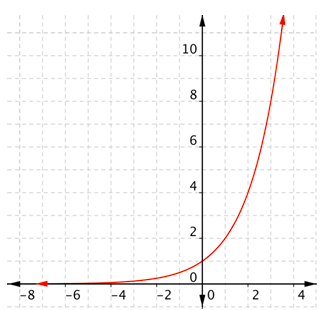
Crecimiento exponencial
Como puedes ver arriba, esta función exponencial tiene una gráfica que se acerca mucho al\(x\) eje -a medida que la gráfica se extiende hacia la izquierda (ya que\(x\) se vuelve más negativa), pero nunca toca realmente el\(x\) eje -eje. Conocer la forma general de las gráficas de funciones exponenciales es útil para graficar ecuaciones o funciones exponenciales específicas.
Hacer una tabla de valores también es útil, ya que puedes usar la tabla para colocar la curva de la gráfica con mayor precisión. Una cosa a recordar es que si una base tiene un exponente negativo, entonces toma el recíproco de la base para hacer positivo al exponente. Por ejemplo,\(4^{-2}=\left(\frac{4}{1}\right)^{-2}=\left(\frac{1}{4}\right)^{2}\).
Problema: Hacer una tabla de valores para\(f(x)=3^{x}\).
Responder
Hacer una “T” para iniciar la mesa con dos columnas. Etiquetar las columnas\(x\) y\(f(x)\).
| \(x\) | \(f(x)\) |
Elija varios valores para\(x\) y colóquelos como filas separadas en la\(x\) columna.
Consejo: Siempre es bueno incluir 0, valores positivos y valores negativos, si puedes.
| \(x\) | \(f(x)\) |
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 |
Evalúe la función para cada valor de\(x\), y escriba el resultado en la\(f(x)\) columna junto al\(x\) valor que utilizó. Por ejemplo, cuando\(x=-2, f(x)=3^{2}=\left(\frac{1}{3}\right)^{2}=\frac{1}{9}\), así\(\frac{1}{9}\) va en la\(f(x)\) columna junto a -2 en la\(x\) columna. \(f(1)=3^{1}=3\), así que 3 va en la\(f(x)\) columna junto a 1 en la\(x\) columna.
| \(x\) | \(f(x)\) |
| -2 | \(\frac{1}{9}\) |
| -1 | \(\frac{1}{3}\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
Tenga en cuenta que su tabla de valores puede ser diferente de la de otra persona, si eligió diferentes números para\(x\).
Mira la tabla de valores. Piensa en lo que sucede a medida que aumentan los\(x\) valores: ¡también lo hacen los valores de función (\(f(x)\)o\(y\))!
Ahora que tienes una tabla de valores, puedes usar estos valores para ayudarte a dibujar tanto la forma como la ubicación de la función. Conecta los puntos lo mejor que puedas para hacer una curva suave (no una serie de líneas rectas). Esto demuestra que todos los puntos de la curva forman parte de esta función.
Problema: Gráfica\(f(x)=3^{x}\).
Responder
Comienza con una tabla de valores, como la del ejemplo anterior.
| \(x\) | \(f(x)\) |
| -2 | \(\frac{1}{9}\) |
| -1 | \(\frac{1}{3}\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
Si piensas en eso\(y\), cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas.\(f(x)\)
| \(x\) | \(f(x)\) | punto |
| -2 | \(\frac{1}{9}\) | (-2,\(\frac{1}{9}\)) |
| -1 | \(\frac{1}{3}\) | (-1,\(\frac{1}{3}\)) |
| 0 | 1 | (0, 1) |
| 1 | 3 | (1, 3) |
| 2 | 9 | (2, 9) |
Trazar los puntos.
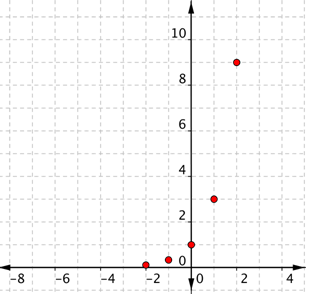
Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica exponencial para ayudarte: esta gráfica se acerca mucho al\(x\) eje -de la izquierda, pero nunca toca realmente el\(x\) eje -y se vuelve cada vez más empinada a la derecha.
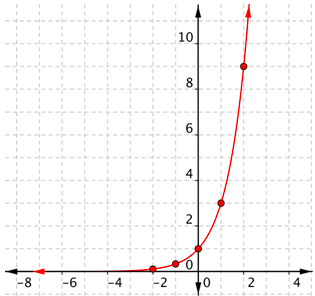
Este es un ejemplo de crecimiento exponencial. A\(x\) medida que aumenta,\(f(x)\) “crece” más rápidamente. Probemos con otro.
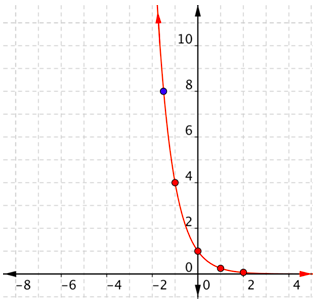
Problema: Gráfica\(f(x)=4^{x}\).
Responder
Comience con una tabla de valores. Puedes elegir diferentes valores, pero una vez más, es útil incluir 0, algunos valores positivos y algunos valores negativos.
Recuerda,\(4^{-2}=\left(\frac{1}{4}\right)^{2}=\frac{1}{16}\).
| \(x\) | \(f(x)\) |
| -2 | \(\frac{1}{16}\) |
| -1 | \(\frac{1}{4}\) |
| 0 | 1 |
| 1 | 4 |
| 2 | 16 |
Si piensas que\(y\) cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas.\(f(x)\)
Trazar los puntos.
Observe que la base más grande en este problema hizo que el valor de la función se disparara. Incluso con\(x\) tan solo 2, el valor de la función es demasiado grande para la escala del eje que usaste antes. Se puede cambiar la escala, pero entonces nuestros otros valores están muy unidos entre sí. También podrías probar otros puntos, como cuándo\(x = \frac{3}{2}\). Porque conoces la raíz cuadrada de 4, puedes encontrar ese valor en este caso:\(4^{\frac{3}{2}}=(\sqrt{4})^{3}=2^{3}=8\)
El punto (\(\frac{3}{2}\), 8) es el punto azul en esta gráfica.
Para otras bases, es posible que necesites usar una calculadora para ayudarte a encontrar el valor de la función.
Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica exponencial para ayudarte: esta gráfica se acerca mucho al\(x\) eje -de la izquierda, pero nunca toca realmente el\(x\) eje -y se vuelve cada vez más empinada a la derecha.
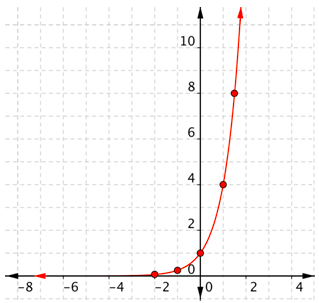
Comparemos las tres gráficas que has visto. Las funciones\(f(x)=2^{x}\),\(f(x)=3^{x}\), y\(f(x)=4^{x}\) están todas graficadas a continuación.
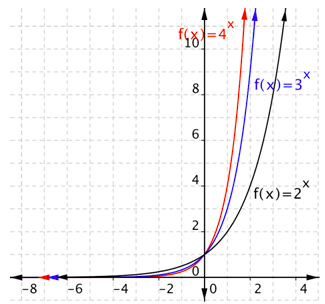
Observe que una base más grande hace que la gráfica sea más pronunciada. Una base más grande también hace que la gráfica se acerque al\(y\) eje\(x > 0\) -y más cerca\(x\) del eje para\(x < 0\). ¡Todas las gráficas pasan por (0, 1)!
Decaimiento exponencial
Recuerda eso para funciones exponenciales,\(b >0\), pero\(b \neq 1\). En los ejemplos anteriores,\(b > 1\). ¿Qué pasa cuando\(b\) está entre 0 y 1,\(0<b<1\)?
Problema: Gráfica\(f(x)=\left(\frac{1}{2}\right)^{x}\).
Responder
Comience con una tabla de valores.
| \(x\) | \(f(x)\) |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | \(\frac{1}{2}\) |
| 2 | \(\frac{1}{4}\) |
¡Cuidado con los exponentes negativos! Recuerda tomar el recíproco de la base para hacer positivo al exponente. En este caso,\(\left(\frac{1}{2}\right)^{-2}=\left(\frac{2}{1}\right)^{2}=2^{2}=4\), y\(\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\).
Usa la tabla como pares ordenados y traza los puntos.
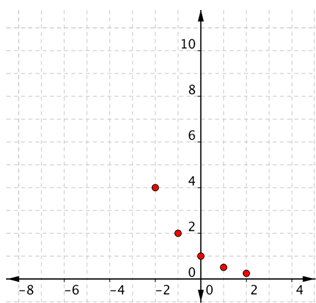
Como los puntos no están en una línea, no se puede usar una recta. Conecta los puntos lo mejor que puedas usando una curva suave (no una serie de líneas rectas).
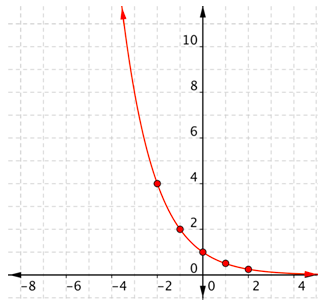
Observe que la forma es similar a la forma cuando\(b > 1\), pero esta vez la gráfica se acerca al\(x\) eje -cuando\(x > 0\), en lugar de cuando\(x < 0\). Esto es decaimiento exponencial. En lugar de que los valores de función “crezcan” a medida que aumentan los valores, como lo hacían antes, los valores de la función “decaigan” o disminuyen a medida que\(x\) aumentan Se acercan cada vez más a 0.
Problema: Graph\(f(x)=\left(\frac{1}{4}\right)^{x}\)
Responder
Crear una tabla de valores. Nuevamente, ten cuidado con los exponentes negativos. Recuerda tomar el recíproco de la base para hacer positivo al exponente. \(\left(\frac{1}{4}\right)^{-2}=\left(\frac{4}{1}\right)^{2}=4^{2}=16\).
| \(x\) | \(f(x)\) |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | \(\frac{1}{2}\) |
| 2 | \(\frac{1}{4}\) |
Observe que en esta tabla, los\(x\) valores aumentan. Los\(y\) valores disminuyen.
Utilice los pares de tablas para trazar puntos. Es posible que desee incluir nuevos puntos, especialmente cuando uno de los puntos de la tabla, aquí (-2, 16), no cabe en su gráfica. Porque conoces la raíz cuadrada de 4, inténtalo\(x = -\frac{3}{2}\). Puedes encontrar ese valor en este caso:\(\left(\frac{1}{4}\right)^{-\frac{3}{2}}=\left(\frac{4}{1}\right)^{\frac{3}{2}}=4^{\frac{3}{2}}=(\sqrt{4})^{3}=2^{3}=8\). El punto (-\(frac{3}{2}\), 8) ha sido incluido en azul. Puede que sientas que es necesario incluir puntos adicionales. También es posible que necesites usar una calculadora, dependiendo de la base.
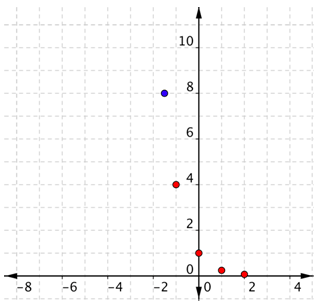
Conecta los puntos lo mejor que puedas, usando una curva suave.
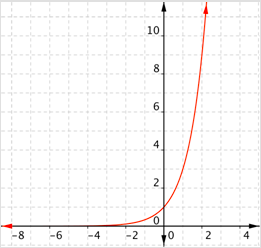
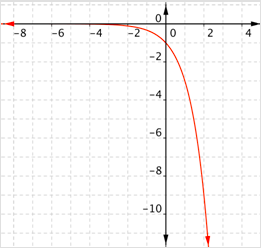
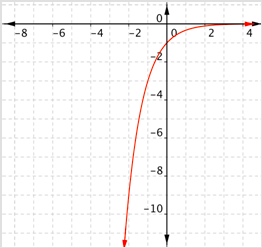
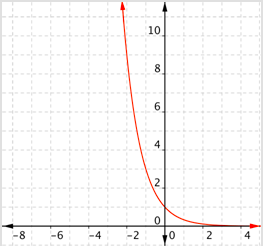
¿Cuál de las siguientes es una gráfica\(f(x) = (\frac{1}{3})^x\)?
- Contestar
-
- Incorrecto. Esta gráfica va en aumento, debido a que los\(y\) valores\(f(x)\) o aumentan a medida que aumentan los\(x\) valores. (Compare los valores para\(x = 1\) y\(x = 2\).) Esta gráfica muestra el crecimiento exponencial, con una base mayor a 1. La respuesta correcta es Gráfica D.
- Incorrecto. Esta gráfica es decreciente, pero todos los valores de las funciones son negativos. El rango para una función exponencial es siempre valores positivos. La respuesta correcta es Gráfica D.
- Incorrecto. Esta gráfica va en aumento, pero todos los valores de las funciones son negativos. La gráfica correcta debe ser decreciente con valores de función positivos. La respuesta correcta es Gráfica D.
- Correcto. Todos los valores de las funciones son positivos, y la gráfica disminuye (mostrando decaimiento exponencial).
Aplicación de funciones exponenciales
Las funciones exponenciales se pueden utilizar en muchos contextos, como el interés compuesto (dinero), el crecimiento de la población y la desintegración radiactiva. En la mayoría de estos, sin embargo, la función no es exactamente de la forma\(f(x) = b^x\). A menudo, esto se ajusta sumando o multiplicando constantes.
Por ejemplo, la fórmula de interés compuesto es\(A=P\left(1+\frac{r}{m}\right)^{m t}\), donde\(P\) está el principal (la inversión inicial que está cobrando intereses) y\(A\) es la cantidad de dinero que tendrías, con intereses, al final de los\(t\) años, utilizando una tasa de interés anual de\(r\) ( expresado como decimal) y períodos\(m\) compuestos por año. En este caso, la base es el valor representado por la expresión\(1+\frac{r}{m}\) y el exponente es\(mt\), un producto de dos valores.
Problema: Si inviertes $1,000 en una cuenta pagando 4% de interés, compuesto trimestralmente, ¿cuánto dinero tendrás después de 3 años?
Contestar
Primero identifique cuál de\(A\),\(P\),\(r\),\(m\), y\(t\) se está pidiendo, luego determine los valores para las variables restantes.
El principal es de $1,000. La tasa es de 4% = 0.04. El tiempo en años es 3. Trimestral compuesto significa 4 veces al año.
El dinero que tendrás después de 3 años será\(A\).
\ (\ begin {array} {c}
P=\ $1000\\
r=0.04\\
m=4\\
t=3
\ end {array}\)
Para encontrar la cantidad, usa la fórmula.
\ (\ begin {array} {l}
A=P\ izquierda (1+\ frac {r} {m}\ derecha) ^ {m t}\\
=1,000\ cdot\ izquierda (1+\ frac {0.04} {4}\ derecha) ^ {4\ cdot 3}\\
=1,000\ cdot (1+0.01) ^ {12}\\
=1,000\ cdot (1.01) ^ 12}\\
= 1,000\ cdot 1.12682503\\
=1,126.82503
\ end {array}\)
Redondear el número al centavo más cercano (centésima). Observe que esto significa que el monto de los intereses devengados después de tres años es de $126.83. ($1,126.83, menos el principal, $1,000).
Tendrás $1,126.83 después de 3 años.
La desintegración radiactiva es un ejemplo de desintegración exponencial. Los elementos radiactivos tienen una vida media. Esta es la cantidad de tiempo que tarda la mitad de una masa del elemento en descomponerse en otra sustancia. Por ejemplo, el uranio-238 es un elemento radiactivo que se descompone lentamente con una vida media de aproximadamente 4.47 mil millones de años. Eso significa que tomará tanto tiempo para que 100 gramos de uranio-238 se conviertan en 50 gramos de uranio-238 (los otros 50 gramos se habrán convertido en otro elemento). ¡Eso es mucho tiempo! En el otro extremo, el radón-220 tiene una vida media de aproximadamente 56 segundos. ¿Qué significa esto? ¡100 gramos de radón-220 se convertirán en 50 gramos de radón-220 y 50 gramos de otra cosa en menos de un minuto!
Dado que la cantidad se reduce a la mitad en cada vida media, se puede usar una función exponencial para describir la cantidad restante a lo largo del tiempo. La fórmula\(R=A\left(\frac{1}{2}\right)^{\frac{t}{h}}\) da la cantidad restante\(R\) a partir de una cantidad inicial\(A\), donde\(h\) está la vida media del elemento y\(t\) es la cantidad de tiempo transcurrido (usando la misma unidad de tiempo que la vida media).
Problema: El cesio-137 es un elemento radiactivo utilizado en aplicaciones médicas. Tiene una vida media de unos 30 años. Supongamos que un laboratorio tiene 10 gramos de cesio-137. Si no lo usan, ¿cuánto seguirá siendo cesio-137 en 60 años?
Contestar
Identificar los valores conocidos en la fórmula.
\(R\): Este es el valor restante, lo que estás tratando de encontrar.
\(A\): La cantidad inicial fue de 10 gramos.
\(h\): La vida media es de 30 años.
\(t\): La cantidad de tiempo transcurrido es de 60 años. (Tenga en cuenta que esto está en la misma unidad, años, que la vida media.)
Usa la fórmula.
\ (\ begin {array} {l}
R=A\ izquierda (\ frac {1} {2}\ derecha) ^ {\ frac {t} {h}}\\
=10\ izquierda (\ frac {1} {2}\ derecha) ^ {\ frac {60} {30}}\\
=10\ izquierda (\ frac {1} {2}\ derecha) ^ {2}\\
=10\ izquierda (\ frac {1} {4}\ derecha)\\
=\ frac {10} {4} =\ frac {5} {2}
\ end {array}\)
Habrá 2.5 gramos de cesio-137 en 60 años.
La madre de Billy puso 100 dólares en una cuenta bancaria para él cuando nació. La cuenta ganó intereses a una tasa de 3% anual, compuesta mensualmente. Asumiendo que no se depositó más dinero y no se retiró ninguno, ¿cuánto dinero habrá en la cuenta cuando Billy cumpla 18 años?
- 170.24
- 171.49
- 8,561.76
- $20,718.34
- Contestar
-
- Incorrecto. Esta es la cantidad cuando la tasa anual se compone anualmente (\(m=1\)). En este caso, estamos componiendo mensualmente,\(m=12\). La respuesta correcta es $171.49.
- Correcto. Utilizando una tasa\(r\) de 0.03 y 12 periodos compuestos por año (\(m=12\)), la fórmula da $171.49.
- Incorrecto. Es posible que haya utilizado\(r=3\) en lugar de\(r=0.03\) para la tasa anual, luego malinterpretó el resultado de su calculadora. La respuesta correcta es $171.49.
- Incorrecto. Es posible que haya utilizado\(r=0.3\) en lugar de\(r=0.03\) para la tasa anual. La respuesta correcta es $171.49.
Resumen
Las funciones exponenciales de la forma\(f(x) = b^x\) aparecen en diferentes contextos, incluyendo finanzas y desintegración radiactiva. La base\(b\) debe ser un número positivo y no puede ser 1. Las gráficas de estas funciones son curvas que aumentan (de izquierda a derecha) si\(b>1\), mostrando crecimiento exponencial, y disminuyen si\(0 < b < 1\), mostrando decaimiento exponencial.