3.1: ¿Qué es una Base de Datos?

La integración de datos de fuentes dispares es un problema importante en la industria hoy en día. Un estudio realizado en 2008 [BH08] mostró que la integración de datos representa el 40% de los presupuestos de TI (tecnología de la información), y que el mercado de software de integración de datos fue de $2.5 mil millones en 2007 y aumentó a una tasa de más de 8% anual. En otras palabras, es un problema mayor; pero ¿qué es?

Una base de datos es un sistema de tablas entrelazadas. Los datos se convierten en información cuando se almacenan en una formación determinada. Es decir, los números y las letras no significan nada hasta que se organizan, muchas veces en un sistema de mesas entrelazadas. Un sistema organizado de tablas entrelazadas se llama base de datos. Aquí hay un ejemplo favorito:

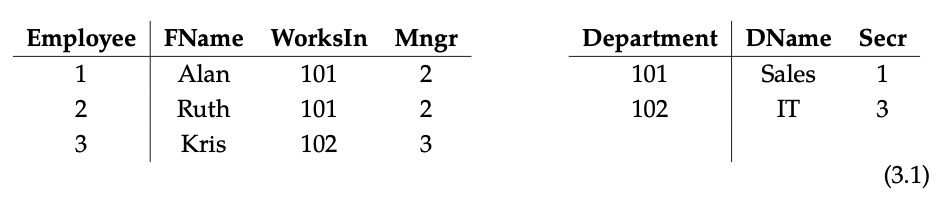
(3.1) Estas dos tablas se entrelazan mediante el uso de una columna especial a la izquierda, demarcada por una línea vertical; se llama columna ID. La columna ID de la primera tabla se llama 'Empleado, 'y la columna ID de la segunda tabla se llama' Departamento '. Las entradas en la columna ID, por ejemplo, 1, 2, 3 o 101, 102, son como etiquetas de fila; indican una fila completa de la tabla en la que se encuentran. Así, cada etiqueta de fila debe ser única (no hay dos filas en una tabla que puedan tener la misma etiqueta), de manera que pueda especificar sin ambigüedades su fila.

La columna de ID de cada tabla, y el conjunto de identificadores únicos que se encuentran en ella, es lo que permite el enclavamiento mencionado anteriormente. En efecto, otras entradas en varias tablas pueden hacer referencia a filas en una tabla dada mediante el uso de su columna ID. Por ejemplo, cada entrada en la columna WorkIn hace referencia a un departamento para cada empleado; cada entrada en la columna Mngr (gerente) hace referencia a un empleado por cada empleado, y cada entrada en la columna Secr (secretario) hace referencia a un empleado para cada departamento. La gestión de todas estas referencias cruzadas es el propósito de las bases de datos.

Mirando hacia atrás en la ecuación (3.1), uno podría notar que cada columna sin ID, que se encuentra en cualquiera de las tablas, es una referencia a una etiqueta de algún tipo. Algunos de estos, a saber, WorkSin, Mngr y Secr, son referencias internas, a menudo llamadas claves externas; hacen referencia a filas (claves) en la columna ID de alguna tabla (foránea). Otros, a saber, fName y DName, son referencias externas; hacen referencia a cadenas o enteros, que también se pueden considerar como etiquetas, cuyo significado se conoce de manera más amplia. Las etiquetas de referencia internas se pueden cambiar siempre que el cambio sea consistente, 1 podría reemplazarse por 1001 en todas partes sin cambiar el significado, ¡mientras que las etiquetas de referencia externas ciertamente no pueden! Cambiar Ruth a Bruce en todas partes cambiaría la forma en que la gente entendía los datos

La estructura de referencia para una base de datos dada, es decir, cómo las tablas se entrelazan a través de claves externas, nos dice algo sobre qué información se pretendía almacenar en ella. Se puede visualizar la estructura de referencia para la Ec. (3.1) gráficamente de la siguiente manera:

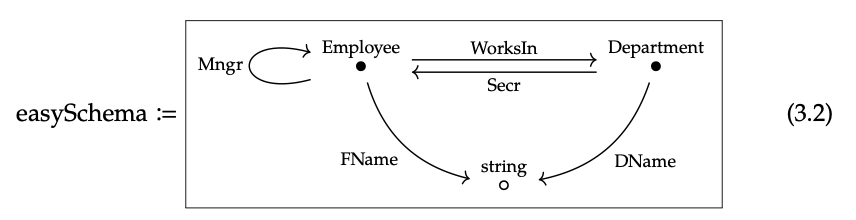
Se trata de una especie de “diagrama de Hasse para una base de datos”, al igual que los diagramas de Hasse para preordenes en Remark 1.39. ¿Cómo deberías leerlo?

Las dos tablas de la Ec. (3.1) están representadas en la gráfica (3.2) por los dos nodos negros, a los que se les da el mismo nombre que las columnas ID: Empleado y Departamento. Hay otro nodo, dibujado de blanco en lugar de negro, que representa el tipo de referencia externa de cadenas, como “Alan”, “Alpha” y “Sales”. Las flechas en el diagrama representan columnas no ID de las tablas; apuntan en la dirección de referencia: workIn refiere a un empleado a un departamento.

Ejercicio 3.3.

Contar el número de columnas sin ID en la Ec. (3.1). Contar el número de flechas (claves foráneas) en la Ec. (3.2). Deberían ser el mismo número en este caso; ¿es esto una coincidencia? ♦

Un diagrama de estilo Hasse como el de la ecuación (3.2) puede llamarse esquema de base de datos; representa cómo se está organizando la información, la formación en la que se guardan los datos. Se pueden agregar reglas, a veces llamadas 'reglas de negocio' al esquema, con el fin de asegurar la integridad de los datos. Si se violan estas reglas, se sabe que los datos que se ingresan no se ajustan a la forma en que pretendían los diseñadores de bases de datos Por ejemplo, los diseñadores pueden hacer cumplir reglas diciendo

• cada secretario de departamento debe trabajar en ese departamento;

• el gerente de cada empleado debe trabajar en el mismo departamento que el empleado.

Al hacerlo, se cambia el esquema, digamos de 'EasySchema' (3.2) a 'MySchema' a continuación.

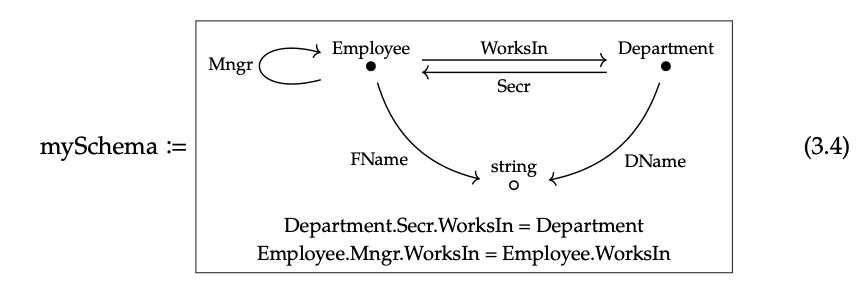
En otras palabras, la diferencia es que EasySchema más restricciones es igual a MySchema. Pronto veremos que los esquemas de bases de datos son categorías C, que los datos en sí están dados por un functor C → Set 'de valores conjuntos, y que las bases de datos pueden mapearse entre sí a través de los funtores C → D. En otras palabras, hay una superposición relativamente grande entre la teoría de bases de datos y la teoría de categorías. Esto se ha elaborado en una serie de ponencias; véase la Sección 3.6. También se ha implementado en software de trabajo, llamado FQL, que significa lenguaje de consulta funtorial. Aquí hay un ejemplo de código FQL para el esquema que se muestra arriba:

Comunicación entre bases de datos. Nosotros hemos dicho que las bases de datos están diseñadas para almacenar información sobre algo. Pero diferentes personas u organizaciones podrían ver el mismo tipo de cosas de diferentes maneras. Por ejemplo, un banco almacena sus registros financieros de acuerdo con las normas europeas y otro lo hace de acuerdo con los estándares japoneses. Si estos dos bancos se fusionan en uno, necesitarán poder compartir sus datos a pesar de las diferencias en la forma de sus esquemas de base de datos.

Tales problemas son enormes e intrincados en general, porque las bases de datos suelen comprender cientos o miles de tablas entrelazadas. Además, estos problemas ocurren con más frecuencia que solo cuando las empresas quieren fusionarse. Es bastante común que una empresa determinada mueva datos entre bases de datos a diario. La razón es que diferentes formas de organizar la información son convenientes para diferentes propósitos. Al igual que empacamos nuestra ropa en una maleta cuando viajamos pero usamos un clóset en casa, generalmente no hay una mejor manera de organizar nada.

La teoría de categorías proporciona un enfoque matemático para traducir entre estas diferentes formas organizacionales. Es decir, formaliza una especie de proceso de reorganización automatizado llamado migración de datos, que toma datos que se ajustan perfectamente a un esquema y los mueve a otro.

Aquí hay un caso sencillo. Imagine que una compañía aérea tiene dos bases de datos diferentes, quizás creadas en diferentes momentos, que tienen aproximadamente los mismos datos.

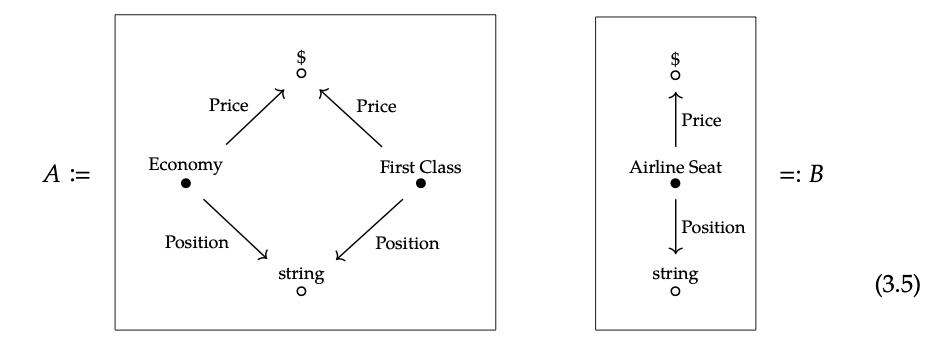
El esquema A tiene más detalles que el esquema B —un asiento de aerolínea puede ser de primera clase o economía— pero son aproximadamente los mismos. Veremos que pueden estar conectados por un functor, y que los datos conformes a A pueden migrarse a través de este functor al esquema B y viceversa.

Las estadísticas al inicio de esta sección muestran que este tipo de problema —cuando ocurre a escala empresarial— sigue resultando difícil y costoso. Si se intenta mover datos de un esquema de origen a un esquema de destino, los datos migrados podrían no encajar en el esquema de destino o no satisfacer algunas de sus restricciones. Esto sucede sorprendentemente a menudo en el mundo de los negocios: se puede pasar una noche moviendo datos, y a la mañana siguiente se encuentra que llegó roto e inadecuado para su uso posterior. De hecho, se cree que más de la mitad de los proyectos de migración de bases de datos fallan.

En este capítulo, discutiremos un método teórico de categoría para migrar datos. Usando categorías y functores, uno puede demostrar por adelantado que una migración de datos dada no fallará, es decir, que se garantiza que el resultado se ajuste al esquema de destino y satisfaga todas sus restricciones.

El material de este capítulo llega al corazón de la teoría de categorías: en particular, discutimos categorías, funtores, transformaciones naturales, adjuntos, límites y colímites. De hecho, muchas de estas ideas han estado presentes en la discusión anterior:

• Las imágenes del esquema, por ejemplo, la Ec. (3.4) representan las categorías C.

• Las instancias, por ejemplo, la Ec. (3.1) son funtores de C a una determinada categoría llamada Set.

• El mapeo implícito en la Ec. (3.5), que lleva asientos económicos y de primera clase en A a asientos de aerolíneas en B, constituye un functor A → B.

• La noción de migración de datos para mover datos entre esquemas es formalizada por funtores adjuntos.

Comenzamos en la Sección 3.2 con la definición de categorías y un montón de

tipo de ejemplos. En la Sección 3.3 traemos de vuelta las bases de datos, en particular sus instancias y los mapas entre ellas, discutiendo funtores y transformaciones naturales. En la Sección 3.4 discutimos la migración de datos a través de adjuntos, que generalizan las conexiones Galois que introdujimos en la Sección 1.4. Por último en la Sección 3.5 damos una sección de bonificación sobre límites y corlímites. \(^{1}\)