3.2: Categorías
- Page ID
- 112288
Una categoría C consta de cuatro piezas de objetos de datos, morfismos, identidades y una regla de composición que satisface dos propiedades.
Para especificar una categoría C:
- uno especifica una colección\(^{2}\) Ob (C), cuyos elementos se denominan objetos.
- por cada dos objetos c, d, se especifica un conjunto C (c, d), cuyos\(^{3}\) elementos se denominan morfismos de c a d.
- para cada objeto c\(\in\) Ob (C), se especifica un morfismo\(id_{c}\) \(\in\)C (c, c), llamado el morfismo de identidad en c.
- por cada tres objetos c, d, e\(\in\) Ob (C) y morfismos f\(\in\) C (c, d) y g\(\in\) C (d, e), se especifica un morfismo f; g \(\in\)C (c, e), denominado compuesto de f y g.
A veces escribiremos un objeto c\(\in\) C, en lugar de c\(\in\) Ob (C). También será conveniente denotar los elementos f\(\in\) C (c, d) como f: c → d. Aquí, c se llama el dominio de f, y d se llama el codominio de f.
Estos componentes deben cumplir dos condiciones:
- unitalidad: para cualquier morfismo f: c → d, componer con las identidades en c o d no hace nada:\(id_{c}\); f = f y f;\(id_{d}\) = f.
- asociatividad: para tres morfismos cualesquiera f: c 0 → c 1, g: c 1 → c 2, y h: c 2 → c 3, los siguientes son iguales: (f; g); h = f; (g; h). Escribimos este compuesto simplemente como f; g; h.
Nuestro siguiente objetivo es dar muchos ejemplos de categorías. Nuestra primera fuente de ejemplos es la de categorías libres y finitamente presentadas, que generalizan la noción de diagrama de Hasse a partir de la observación 1.39.
Categorías Gratuitos
Recordemos de la Definición 1.36 que una gráfica consta de dos tipos de cosas: vértices y flechas. A partir de ahí se pueden definir caminos, que son solo secuencias de flechas de cabeza a cola. Cada ruta p tiene un vértice inicial y un vértice final; si p va de v a w, escribimos p: v → w. A cada vértice v, hay un camino trivial, que no contiene flechas, comenzando y terminando en v; a menudo lo denotamos por id v o simplemente por v. También podemos concatenar caminos: dado p: v → w y q: w → x, su concatenación se denota p = q, y va v → x.
En el Capítulo 1, usamos gráficas para representar preordenes (V, ≤): los vértices forman los elementos del preorden, y decimos que v ≤ w si hay una ruta de v a w en G. Ahora utilizaremos gráficos de manera muy similar para representar ciertas categorías, conocidas como categorías libres. Después explicaremos una fuerte relación entre preórdenes y categorías en la Sección 3.2.3.
Para cualquier gráfica G = (V, A, s, t), podemos definir una categoría Libre (G), llamada la categoría libre en G, cuyos objetos son los vértices V y cuyos morfismos a partir de c a d son los caminos de c a d. El morfismo identitario sobre un objeto c es simplemente el camino trivial en c. La composición viene dada por la concatenación de caminos.
Por ejemplo, definimos 2 como la categoría libre generada por la gráfica que se muestra a continuación:
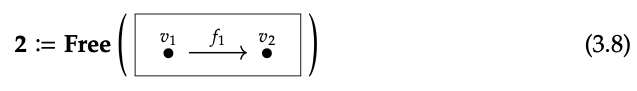
Tiene dos objetos\(v_{1}\) y\(v_{2}\), y tres morfismos:\(id_{v1}\):\(v_{1}\) →\(v_{1}\),\(f_{1}\):\(v_{1}\) →\(v_{2}\), y\(id_{v2}\):\(v_{2}\) →\(v_{2}\). Aquí\(id_{v1}\) está el camino de longitud 0 comenzando y terminando en\(v_{1}\),\(f_{1}\) es el camino de longitud 1 que consiste solo en la flecha\(f_{1}\), y\(id_{v2}\). Como sugiere nuestra notación,\(id_{v1}\) es el morfismo de identidad para el objeto\(v_{1}\), y de manera similar\(id_{v2}\) es la longitud 0 camino en\(v_{2}\).
Como sugiere nuestra notación,\(id_{v1}\) es el morpismo identitario para el objeto\(v_{1}\), y similar\(id_{v2}\) para\(v_{2}\). Como la composición viene dada por concatenación, tenemos, por ejemplo\(id_{v1}\);\(f_{1}\) =\(f_{1}\),\(id_{v2}\);\(id_{v2}\) =\(id_{v2}\), y así sucesivamente.
A partir de ahora, podremos eliminar la diferencia entre una gráfica y la categoría libre correspondiente Libre (G), al menos cuando la que queremos decir sea lo suficientemente clara desde el contexto.
Para que Free (G) sea realmente una categoría, debemos verificar que estos datos que especificamos obedezcan a las propiedades de unitalidad y asociatividad. Verifique que estos sean obedecidos para cualquier gráfica G. ♦
La categoría libre en la gráfica que se muestra aquí:\(^{4}\)

tiene tres objetos y seis morfismos: los tres vértices y seis caminos en la gráfica. Crear seis nombres, uno por cada uno de los seis morfismos en 3. Escriba una tabla de seis por seis, etiquete las filas y columnas por los seis nombres que elija.
- Rellene la tabla escribiendo el nombre del compuesto en cada celda, cuando haya un compuesto.
- ¿Dónde están las identidades? ♦
Hagamos algunas definiciones, basadas en el patrón anterior:
- ¿Cuál es la categoría 1? Es decir, ¿cuáles son sus objetos y morfismos?
- ¿Cuál es la categoría 0?
- ¿Cuál es la fórmula para el número de morfismos en n para n arbitrario\(\in\)\(\mathbb{N}\)? ♦
Considera la siguiente gráfica:

Tiene sólo un vértice y una flecha, pero tiene infinitamente muchos caminos. De hecho, tiene una ruta única de longitud n para cada número natural n\(\in\) N. Es decir, Path = {z, s, (s; s), (s; s; s),...}, donde escribimos z para la ruta de longitud 0 en z; representa el morfismo id z. Hay una correspondencia uno a uno entre Path y los números naturales, N = {0, 1, 2, 3,.}.
Este es un ejemplo de una categoría con un objeto. Una categoría con un objeto se llama monoide, noción que discutimos primero en el Ejemplo 2.6. Ahí dijimos que un monoide es una tupla (M, ∗, e) donde ∗: M × M → M es una función y e\(\in\) M es un elemento, y m ∗ 1 = m = 1 ∗ m y (m ∗ n) ∗ p = m ∗ (n ∗ p).
Las dos nociones pueden verse superficialmente diferentes, pero es fácil describir la conexión.
Dada una categoría C con un objeto, digamos •, let M = C (•, •), let e =\(id_{•}\), y let ∗: C (•, •) × C (•, •) → C (•, •) sea la operación de composición ∗ =;. Se cumplirán los requisitos de asociatividad y unidad para el monoide porque C es una categoría.
En el Ejemplo 3.13 identificamos las rutas de la gráfica de bucle (3.14) con números n\(\in\)\(\mathbb{N}\). Los caminos se pueden concatenar. Dados los números m, n\ (\ in\)\(\mathbb{N}\), ¿qué número corresponde a la concatenación de sus rutas asociadas? ♦
Presentación de categorías a través de ecuaciones de ruta
Entonces, para cualquier gráfica G, hay una categoría gratuita en G. Pero no tenemos que detenernos ahí: podemos agregar ecuaciones entre caminos en la gráfica, y aún así obtener una categoría. Solo se nos permite igualar dos caminos p y q cuando son paralelos, es decir, tienen el mismo vértice de origen y el mismo vértice de destino.
Una gráfica finita con ecuaciones de trayectoria se denomina presentación finita para una categoría, y la categoría que da como resultado se conoce como una categoría finitamente presentada. Aquí hay dos ejemplos:
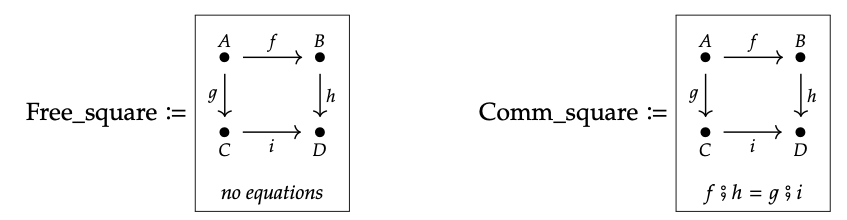
Ambas son presentaciones de categorías: en la de la izquierda, no hay ecuaciones por lo que presenta una categoría libre, como se discute en la Sección 3.2.1. La categoría cuadrada libre tiene diez morfismos, porque cada camino es un morfismo único.
- Anota los diez caminos en la categoría de cuadrado libre anterior.
- Nombra dos caminos diferentes que sean paralelos.
- Nombra dos caminos distintos que no sean paralelos. ♦
Por otra parte, la categoría presentada a la derecha tiene sólo nueve morfismos, porque f; h y g; i se hacen iguales. A esta categoría se le llama el “cuadrado conmutativo”. Sus morfismos son
{A, B, C, D, f, g, h, i, f; h}
Se podría decir “el que falta es g; i”, pero eso no es del todo correcto: g; i también está ahí, porque es igual a f; h. Como es habitual, A denota\(id_{A}\), etc.
Anota todos los morfismos en la categoría que presenta el siguiente diagrama:
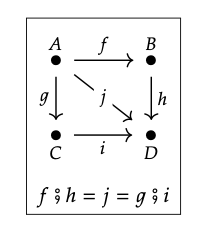 ♦
♦
También debemos ser conscientes de que hacer cumplir una ecuación entre dos mor- fismos a menudo implica ecuaciones adicionales. Aquí hay dos ejemplos más de presentaciones, en las que ocurre este fenómeno:
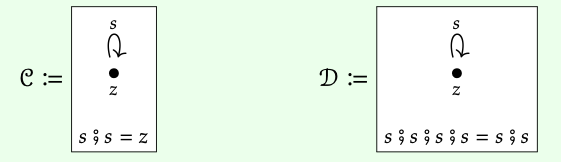
En C tenemos la ecuación s; s = z. Pero esto implica s; s; s = z; s = s! Y de manera similar tenemos s; s; s; s = z; z = z. El conjunto de morfismos en C es de hecho meramente {z, s}, con composición descrita por s; s = z; z = z, y z; s = s; z = s. En teoría de grupos, se hablaría de un grupo llamado\(\mathbb{Z}\) /2\(\mathbb{Z}\).
Anota todos los morfismos de la categoría D del Ejemplo 3.18. ♦
Obración 3.20. Ahora podemos ver que los esquemas de la Sección 3.1, por ejemplo, las ecuaciones (3.2) y (3.4) son presentaciones finitas de categorías. Volveremos a esta idea en la Sección 3.3.
Prepedidos y categorías gratuitas: dos extremos de un espectro
Ahora que hemos utilizado gráficas para representar los pedidos por adelantado en el Capítulo 1 y las categorías anteriores, es posible que uno quiera conocer la relación entre estos dos usos. La idea principal que queremos explicar ahora es que
“Un preorden es una categoría donde cada dos flechas paralelas son iguales”.
Por lo tanto, cualquier preorden puede considerarse como una categoría, y cualquier categoría puede ser de alguna manera “aplastada” en una preorden. Discutamos estas ideas.
Prepedidos como categorías. Supongamos que (P, ≤) es un preorden. Se especifica una categoría P de la siguiente manera. Los objetos de P son precisamente los elementos de P; es decir, Ob (P) = P. En cuanto a los morfismos, P tiene exactamente un morfismo p → q si p ≤ q y no hay morfismos p → q si p\(\nleq\) q. El hecho de que ≤ sea reflexivo asegura que cada objeto tenga una identidad, y el hecho de que ≤ sea transitivo asegura que los morfismos puedan ser compuestos. Llamamos a P la categoría correspondiente al preorden (P, ≤).
De hecho, un diagrama de Hasse para un preorden puede pensarse en una presentación de una categoría donde, para todos los vértices p y q, cada dos caminos de p → q se declaran iguales. Por ejemplo, en la Ec. (1.5) vimos un diagrama de Hasse que era como el gráfico de la izquierda:
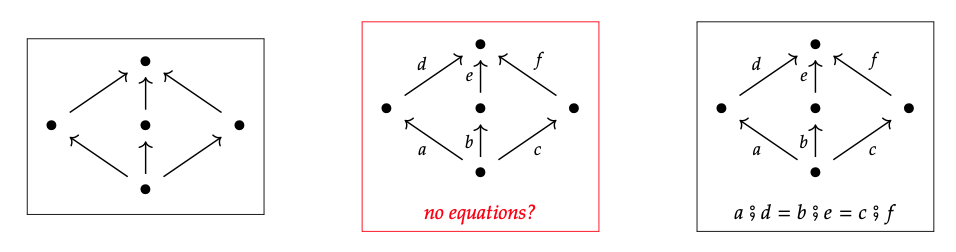
El diagrama de Hasse (izquierda) podría parecerse más a la presentación de categoría libre (media) que no tiene ecuaciones, pero eso no es correcto. La categoría libre tiene tres morfismos (caminos) de objeto inferior a objeto superior, mientras que los preordenes son categorías con como máximo un morfismo entre dos objetos dados. En cambio, el diagrama de la derecha, con estos caminos de abajo hacia arriba iguales, es la presentación correcta para el preorden de la izquierda.
¿Qué ecuaciones necesitarías agregar a las gráficas a continuación para presentar los preordenes asociados?

El reflejo de preorden de una categoría. Dada cualquier categoría C, se puede obtener un preorden (C, ≤) de ella destruyendo la distinción entre dos morfismos paralelos cualesquiera. Es decir, vamos C: = Ob (C), y poner\(c_{1}\) ≤\(c_{2}\) iff C (\(c_{1}\), \(c_{2}\))\(\neq\) Ø. Si hay uno, o dos, o cincuenta, o infinitamente muchos morfismos\(c_{1}\) →\(c_{2}\) en C, la reflexión de preorden no ve la diferencia. Pero sí ve la diferencia entre algunos morfismos y no morfismos.
¿Cuál es el reflejo de preorden de la categoría\(\mathbb{N}\) del Ejemplo 3.13? ♦
Solo hemos hablado de funtores colindantes entre preordenes, pero pronto discutiremos los anexos en general. Aquí hay una declaración que quizás no entiendas exactamente, pero es verdad; puedes preguntarle a un experto en teoría de categorías al respecto y ellos deberían poder explicarte:
Considerar un preorden como categoría es justo junto a convertir una categoría en un preorden por reflexión de preorden.
Comentario 3.23 (Extremos de un espectro). El punto principal de esta subsección es que tanto las preórdenes como las categorías libres se especifican mediante una gráfica sin ecuaciones de trayectoria, pero denotan extremos opuestos de un espectro. En ambos casos, los vértices de la gráfica se convierten en objetos de una categoría y los caminos se convierten en morfismos. Pero en el caso de las categorías libres, no hay ecuaciones por lo que cada camino se convierte en un morfismo diferente. En el caso de los pedidos por adelantado, todos los caminos paralelos se convierten en el mismo morfismo. Cada presentación de categoría, es decir, gráfica con algunas ecuaciones, se encuentra en algún lugar entre la categoría libre (sin ecuaciones) y su reflexión de preorden (todas las ecuaciones posibles).
Categorías importantes en matemáticas
Hemos estado hablando de presentaciones de categorías, pero hay categorías que se entienden mejor directamente, no a modo de presentaciones. Recordemos la definición de categoría
de la Definición 3.6. La categoría más importante en matemáticas es la categoría de conjuntos.
La categoría de conjuntos, denotada Set, se define de la siguiente manera.
(i) Ob (Set) es la colección de todos los conjuntos.
(ii) Si S y T son conjuntos, entonces Set (S, T) = {f: S → T | f es una función}.
(iii) Para cada conjunto S, el morfismo de identidad es la función\(id_{S}\): S → S dada por\(id_{S}\) (s) := s para cada s\(\in\) S.
(iv) Dado f: S → T y g: T → U, su compuesto es la función f; g: S → U dada por (f; g) (s) := g ( f (s)).
Estas definiciones satisfacen las condiciones de unidad y asociatividad, por lo que Set es efectivamente una categoría.
Muy relacionada está la categoría FinSet. Esta es la categoría cuyos objetos son conjuntos finitos y cuyos morfismos son funciones entre ellos.
Vamos\(\underline{2}\) = {1, 2} y\(\underline{3}\) = {1, 2, 3}. Se trata de objetos en la categoría Conjunto discutidos en la Definición 3.24. Anota todos los elementos del conjunto Set (\(\underline{2}\),\(\underline{3}\)); debería haber nueve. ♦
Obración 3.26. Quizás te hayas preguntado qué categorías tienen que ver con las categorías V (Definición 2.46); quizás pienses que las definiciones apenas se parecen. A pesar del término 'categoría enriquecida', las categorías V no son categorías con estructura extra. Si bien algunos tipos de categorías V, como las categorías Bool, es decir, los pedidos por adelantado, pueden verse naturalmente como categorías, otros tipos, como las categorías de costo, no pueden.
La razón de la importancia de Set es que, si generalizamos la definición de categoría enriquecida (Definición 2.46), encontramos que las categorías en el sentido de Definición 3.6 son exactamente Set -categorías entonces las categorías son categorías V para una elección muy especial de V. Volveremos a esto en la Sección 4.4.4. Por ahora, simplemente comentamos que al igual que una comprensión profunda de la categoría Costo, por ejemplo, saber que se trata de una quantale produce una visión de los espacios métricos de Lawvere, por lo que el estudio de Set produce información sobre categorías.
Hay muchas otras categorías que preocupan a los matemáticos:
- Top: la categoría de espacios topológicos (barrio)
- Grph: la categoría de gráficas (conexión)
- Meas: la categoría de espacios de medida (cantidad)
- Lun: la categoría de monoides (acción)
- Grp: la categoría de grupos (acción reversible, simetría)
- Cat: la categoría de categorías (acción en contexto, estructura)
Pero, de hecho, esto no le hace justicia en absoluto a la diversidad de categorías en las que piensan los matemáticos. Trabajan con cualquier categoría que encuentren que se ajuste a su propósito en ese momento, como 'la categoría de colectores riemannianos conectados de dimensión a lo sumo 4'.
Aquí hay una fuente más de ejemplos: toma cualquier categoría que ya tengas y revierte todos sus morfismos; el resultado vuelve a ser una categoría.
Que C sea una categoría. Su opuesto, denotado\(C^{op}\), es la categoría con los mismos objetos, Ob (\(C^{op}\)) := Ob (C), y para dos objetos cualesquiera c, d\(\in\) Ob (C), uno tiene\(C^{op}\) (c, d) := C (d, c). Las identidades y la composición son como en C.
Isomorfismos en una categoría
Las secciones anteriores han tratado sobre ejemplos de categorías: categorías libres, categorías presentadas y categorías importantes en matemáticas. En esta sección, cambiamos de marcha brevemente y hablamos de un concepto importante en la teoría de categorías, a saber, el concepto de isomorfismo.
En una categoría, suele existir la idea de que dos objetos son intercambiables. Por ejemplo, en la categoría Set, se puede intercambiar el conjunto {, □} por el conjunto {0, 1} y todo será igual, salvo los nombres para los elementos. Del mismo modo, si uno tiene un preorden con los elementos a, b, tal que a ≤ b y b ≤ a, es decir a\(\cong\) b, entonces a y b son esencialmente los mismos. ¿Cómo es así? Pues actúan igual, en que para cualquier otro objeto c, sabemos que c ≤ a iff c ≤ b, y c ≥ a iff c ≥ b. La noción de isomorfismo formaliza esta noción de intercambiabilidad.
Un isomorfismo es un morfismo f: A → B tal que existe un morfismo g: B → A satisfactorio f; g =\(id_{A}\) y g; f\(id_{B}\). En este caso llamamos f y g inversos, y a menudo escribimos g =\(f^{−1}\), o equivalentemente f =\(g^{−1}\). También decimos que A y B son objetos isomórficos.
El conjunto A: = {a, b, c} y el conjunto\(\underline{3}\) = {1, 2, 3} son isomórficos; es decir, existe un isomorfismo f: A →\(\underline{3}\) dado por f (a) = 2, f (b) = 1, f (c) = 3. Los isomorfismos en la categoría Set son las bijecciones.
Recordemos que la cardinalidad de un conjunto finito es el número de elementos en él. Esto se puede entender en términos de isomorfismos en FinSet. Es decir, para cualquier conjunto finito A\(\in\) FinSet, su cardinalidad es el número n\(\in\)\(\mathbb{N}\) tal que existe un isomorfismo A\(\cong\) n. Georg Cantor definió la cardinalidad de cualquier conjunto X como su clase de isomorfismo, es decir, la clase de equivalencia que consiste en todos los conjuntos que son isomórficos a X.
1. ¿Cuál es la inversa\(f^{−1}\):\(\underline{3}\) → A de la función f dada en el Ejemplo 3.29?
2. ¿Cuántos isomorfismos distintos hay A →\(\underline{3}\)? ♦
Mostrar que en cualquier categoría C dada, para cualquier objeto c\(\in\) C dado, la identidad id c es un isomorfismo ♦
Recordemos los Ejemplos 3.13 y 3.18. Un monoide en el que cada morfismo es un isomorfismo se conoce como grupo.
1. ¿El monoide en el Ejemplo 3.13 es un grupo?
2. ¿Qué pasa con el monoide C en el Ejemplo 3.18? ♦
Que G sea una gráfica, y que Free (G) sea la categoría libre correspondiente. Alguien te dice que los únicos isomorfismos en Libre (G) son los morfismos de identidad. ¿Esa persona es correcta? ¿Por qué o por qué no? ♦
En este ejemplo, veremos que es posible que g y f sean casi pero no del todo inversos, en cierto sentido.
Considere las funciones f:\(\underline{2}\) →\(\underline{3}\) y g:\(\underline{3}\) →\(\underline{2}\) dibujadas a continuación:
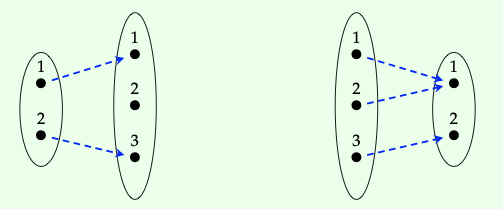
Entonces el lector debería poder verificar instantáneamente que f; g =\(id_{\underline{2}}\) pero g; f\(\neq\)\(id_{\underline{3}}\). Así f y g no son inversos y por lo tanto no isomorfismos. No vamos a necesitar esta terminología, pero los teóricos de las categorías dirían que f y g forman una retracción.


