4.1: ¿Podemos construirlo?

Al diseñar un sistema a gran escala, se unen muchos campos diferentes de especialización para trabajar en un solo proyecto. Así, todo el equipo del proyecto se divide en múltiples subequipos, cada uno de los cuales está trabajando en un subproyecto. Y recurrimos a la baja: el subproyecto vuelve a ser factorizado en subproyectos, cada uno con su propio equipo. Uno podría referirse a este tipo de proceso de diseño jerárquico como diseño colaborativo, o co-diseño. En este capítulo, se discute una teoría matemática del codiseño, debido a Andrea Censi [Cen15].

Considera solo un nivel de esta jerarquía: un proyecto y un conjunto de equipos trabajando en él. Se supone que cada equipo debe proporcionar recursos, a veces llamados “funcionalidades”, al proyecto, pero el equipo también requiere recursos para hacerlo. Se debe permitir que diferentes equipos de diseño planifiquen y trabajen independientemente unos de otros para que se avance. Sin embargo, las decisiones de diseño tomadas por un grupo afectan las decisiones de diseño que otros pueden tomar: si A quiere más espacio para proporcionar un mejor altavoz de radio, entonces B debe usar menos espacio. Entonces, estos equipos, aunque ostensiblemente trabajan de manera independiente, dependen unos de otros después de todo.

La combinación de dependencia e independencia es crucial para que se avance y, sin embargo, puede causar grandes problemas. Cuando un equipo requiere más recursos de los que originalmente esperaba requerir, o si no puede proporcionar los recursos que originalmente afirmó que podría proporcionar, la respuesta habitual es que el equipo emita un aviso de cambio de diseño. Pero estos afectan a los equipos vecinos: si el equipo A ahora requiere más de lo reclamado originalmente, el equipo B puede tener que cambiar su diseño, lo que a su vez puede afectar al equipo C. Por lo tanto, estos avisos de cambio de diseño pueden atravesar el sistema a través de bucles de retroalimentación y pueden hacer que los proyectos completos fallen [S+15].

Como ejemplo, considere el problema de diseño de crear un robot para llevar alguna carga a cierta velocidad. El planificador de alto nivel divide el problema en tres equipos de diseño: equipo de chasis, equipo motor y equipo de batería. Cada uno de estos equipos podría dividirse en múltiples partes y el proceso repetido, pero permanezcamos en el nivel superior y consideremos los recursos producidos y los recursos requeridos por cada uno de nuestros tres equipos.

El chasis en cierto sentido proporciona toda la funcionalidad que lleva la carga a la velocidad, pero requiere algunas cosas para hacerlo. Requiere dinero para construir, claro, pero más al punto requiere una fuente de torque y velocidad. Estos son suministrados por el motor, que a su vez necesita voltaje y corriente de la batería. Tanto el motor como la batería cuestan dinero, pero lo más importante es que necesitan ser transportados por el chasis: se convierten en parte de la carga. Se crea un bucle de retroalimentación: el chasis debe llevar todo el peso, incluso el de las partes que alimentan el chasis. Una batería más pesada podría proporcionar más energía para alimentar el chasis, pero ¿la potencia adicional vale la pena la carga más pesada?

En la siguiente imagen, cada parte del chasis, motor, batería y robot se muestra como una caja con puertos a la izquierda y a la derecha. Las funcionalidades, o recursos producidos por la parte se muestran como puertos a la izquierda de la caja, y los recursos requeridos por la parte se muestran como puertos a su derecha.

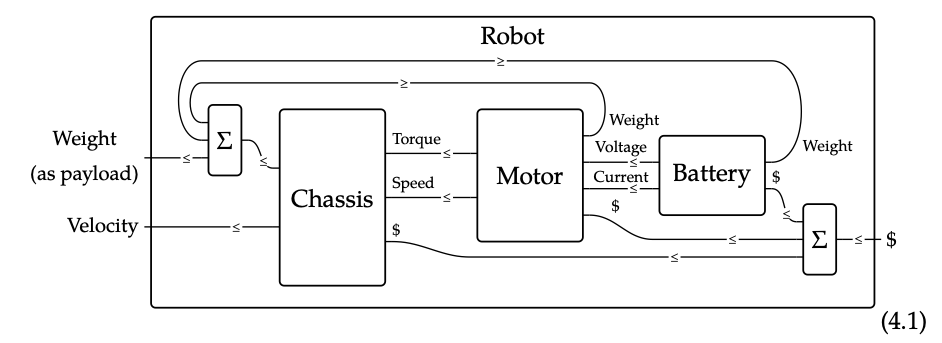
(4.1) Las casillas marcadas\(\Sigma\) corresponden a entradas sumadoras. Estas cajas no van a diseñarse, pero veremos más adelante que encajan fácilmente en el mismo marco conceptual. Tenga en cuenta también las ≤ en cada cable; indican que si la casilla A requiere un recurso que produce la caja B, entonces el requisito de A debe ser menor o igual a la producción de B. El

el chasis requiere par, y el motor debe producir al menos ese par.
Para formalizar esto un poco más, llamemos a diagramas como el de arriba diagramas de codiseño. Cada uno de los cables en un diagrama de codiseño representa un preorden de recursos. Por ejemplo, en la Ecuación (4.1) cada cable corresponde a un tipo de recurso (pesos, velocidades, pares, velocidades, costos, voltajes y corrientes) donde los recursos de cada tipo se pueden ordenar de menos útiles a más útiles.

En general, estos pedidos anticipados no tienen que ser órdenes lineales, aunque en los casos anteriores cada uno probablemente corresponderá a un orden lineal: $10 ≤ $20, 5W ≤ 6W, y así sucesivamente.

Cada una de las cajas en un diagrama de co-diseño corresponde a lo que llamamos una relación de factibilidad. Una relación de viabilidad relaciona la producción de recursos con los requisitos. Por cada par (p, r)\(\in\) P × R, donde P es el preorden de los recursos a producir y R es el preorden de los recursos a ser requeridos, la casilla dice “verdadero” o “falso” —factible o inviable— para ese par. En otras palabras, “sí puedo proporcionar p dado r” o “no, no puedo proporcionar p dado r”.

Por lo tanto, las relaciones de factibilidad definen una función Φ: P × R → Bool. Para que una función Φ: P × R → Bool tenga sentido como relación de factibilidad, sin embargo, hay dos condiciones:

1. Si Φ (p, r) = verdadero y p ′ ≤ p, entonces Φ (p ′, r) = verdadero.
2. Si Φ (p, r) = verdadero y r ≤ r ′, entonces Φ (p, r ′) = verdadero.

Estas condiciones, que volveremos a ver en la Definición 4.2, dicen que si puedes producir p recursos dados r, puedes (a) también producir menos p ′ ≤ p con los mismos recursos r, y (b) también producir p dado más recursos r ′ ≥ r.

Veremos que estas dos condiciones se formalizan al requerir que Φ sea un mapa monótona P\(^{op}\) × R → Bool.

Un problema de co-diseño, representado por un diagrama de co-diseño, nos pide encontrar la posición de algunas relaciones de factibilidad. Pregunta, por ejemplo, dadas estas capacidades de los equipos de chasis, motor y batería, ¿podemos construir un robot juntos? De hecho, un diagrama de codiseño faceta un problema, por ejemplo, el de diseñar un robot, en subproblemas interrelacionados, como en la ecuación (4.1). Una vez elaborada la relación de factibilidad para cada uno de los subproblemas, es decir, las cajas internas en el diagrama, las matemáticas proporcionan un algoritmo que produce la relación de factibilidad de toda la caja externa. Este proceso puede recurrirse a la baja, desde el mayor problema hasta pequeños subproblemas.

En este capítulo, entenderemos los problemas de co-diseño en términos de pro- funtores enriquecidos, en particular Bool -profunctors. Un Bool -profunctor es como un puente que conecta una preorden a otra. Mostraremos cómo el marco de codiseño da lugar a una estructura conocida como categoría compacta cerrada, y que cualquier categoría compacta cerrada puede interpretar los tipos de diagramas de cableado que vemos en la Ec. (4.1).