4.2: Profuntores enriquecidos
- Page ID
- 112150
En esta sección entenderemos cómo los problemas de co-diseño forman una categoría. En el camino desarrollaremos alguna maquinaria abstracta que nos permitirá reemplazar espacios de diseño de preordenar por otras categorías enriquecidas.
Relaciones de factibilidad como Bool -profunctors
La teoría del co-diseño se basa en preordenes: cada recurso, por ejemplo, velocidad, par o $ se estructura como un preorden. El orden x ≤ y representa la disponibilidad de x dado y, es decir, que siempre que tengas y, también tengas x. Por ejemplo, en nuestro preorden de potencia, si 5W ≤ 10W, significa que cada vez que nos proporcionan 10W, implícitamente también tenemos 5W. Arriba nos referimos a esto como un orden de menos útil a más útil: si x siempre está disponible dado y, entonces x es menos útil que y.
Sabemos por la Sección 2.3.2 que una preorden X puede concebirse como una categoría Bool. Dado x, y\(\in\) X, tenemos X (x, y)\(\in\)\(\mathbb{B}\); este valor responde a la aserción “x está disponible dado y”, marcándolo verdadero o falso.
Nuestro objetivo es ver las relaciones de factibilidad como Bool -profunctors, que son un caso especial de algo llamado profunctors enriquecidos. En efecto, esperamos que este capítulo le dé cierta intuición para los profunctores, surgiendo de la mesa

Debido a que los profunctores enriquecidos son un poco abstractos, primero discutimos concretamente Bool -profunctors como relaciones de factibilidad.
Recordemos que si X = (X, ≤) es un preorden, entonces su opuesto X\(^{op}\) = (X, ≥) tiene x ≥ y iff y ≤ x.
Sea X = (X, ≤ X) e Y = (Y, ≤ Y) sean pedidos por adelantado. Una relación de factibilidad para X dada Y es un mapa monótona
Φ: X\(^{op}\) × Y → Bool. (4.3)
Denotamos esto por Φ: X\(\rightarrow\) Y.
Dado x\(\in\) X e y\(\in\) Y, si Φ (x, y) = verdadero decimos x se puede obtener dado y.
Como se mencionó en la introducción, el requisito de que Φ sea monótono dice que si \(_{X}\)x ′ ≤ x e \(_{Y}\)y ≤ y ′ entonces Φ (x, y) ≤\(_{Bool}\) Φ (x ′, y ′) . En otras palabras, si x se puede obtener dado y, y si x ′ está disponible dado x, entonces x ′ se puede obtener dado y. Y si además y está disponible dado y ′, entonces x ′ también se puede obtener dado y ′.
Ejercicio 4.4.
Supongamos que tenemos los pedidos por adelantado
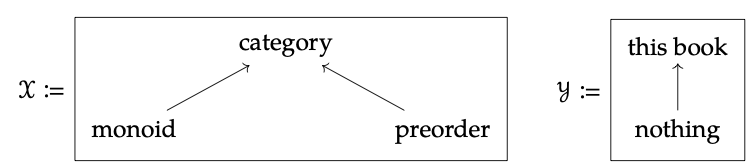
1. Dibuja el diagrama de Hasse para el preorden X\(^{op}\) × Y.
2. Anota un profunctor\(\bigwedge\): X\(\rightarrow\) Y y, leyendo\(\bigwedge\) (x, y) = true como “mi tía puede explicar una x dada y”, dar una interpretación del hecho de que la preimagen de true forma un conjunto superior en X\(^{op}\) × Y. ♦
Para generalizar la noción de relación de factibilidad, debemos notar que el preorden monoidal simétrico Bool tiene más estructura que solo la de un preorden monoidal simétrico: como se menciona en el Ejercicio 2.93, Bool es un cuantale. Eso significa que tiene todas las juntas\(\bigvee\), y una operación de cierre, que escribiremos ⇒:\(\mathbb{B}\) ×\(\mathbb{B}\) →\(\mathbb{B}\). Por definición, esta operación satisface el inmueble que para todos b, c, d\(\in\)\(\mathbb{B}\) uno tiene
b\(\bigwedge\) c ≤ d iff b ≤ (c ⇒ d). (4.5)
La operación ⇒ viene dada por la siguiente tabla:
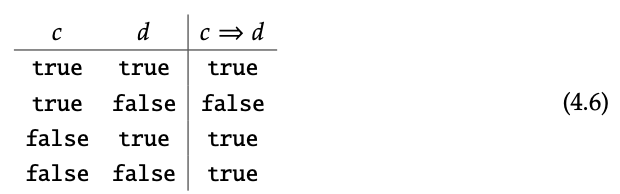
Ejercicio 4.7.
Mostrar que ⇒ como se define en la Ec. (4.6) efectivamente satisface la Ec. (4.5) . ♦
A nivel abstracto, es el hecho de que Bool es una quantale que hace que todo en este capítulo funcione; cualquier otra quantale (unital conmutativa) también define una manera de interpretar diagramas de codiseño. Por ejemplo, podríamos usar el Quantale Cost, que describiría no si x está disponible dado y sino el costo de obtener x dado y; ver Ejemplo 2.37 y Definición 2.46.
Profuntores V
Ya estamos listos para reformular la Ec. (4.3) en términos abstractos. Recordemos las nociones de producto enriquecido (Definición 2.74), functor enriquecido (Definición 2.69) y quantale (Definición 2.79).
Sea V = (V, ≤, I,) a (conmutativa unital) quantale,\(^{1}\) y deje que X e Y sean categorías V.
Un profunctor V de X a Y, denotado Φ: X Y, es un funtor V
Φ: X\(^{op}\) × Y → V.
Tenga en cuenta que un V-functor debe tener categorías V para dominio y codominio, así que aquí estamos considerando V como enriquecido en sí mismo; ver Observación 2.89.
Ejercicio 4.9.
Mostrar que un Profunctor V (Definición 4.8) es lo mismo que una función Φ: Ob (X) × Ob (Y) → V tal que para cualquier x, x ′\(\in\) X e y, y ′\(\in\) Y la siguiente desigualdad se mantiene en V:
X (x ′, x) Φ (x, y) Y (y, y ′) ≤ Φ (x ′, y ′) . ♦
Ejercicio 4.10.
¿Es cierto que un Bool -profunctor, como en la Definición 4.8, es exactamente lo mismo que una relación de factibilidad, como en la Definición 4.2, una vez que se despega toda la jerga? ¿O hay alguna diferencia sutil? ♦
Sabemos que la Definición 4.8 es bastante abstracta. Pero no tengas miedo, te llevaremos a través de él en fotos.
Discutamos Defi- nición 4.8 en el caso V = Bool. Una forma de imaginar un Bool -profunctor Φ: X → Y es en términos de construir puentes entre dos ciudades. Recordemos que un preorden (una categoría Bool) se puede dibujar usando un diagrama de Hasse. Pensaremos en el preorden como una ciudad, y cada vértice en ella como algún punto de interés. Una flecha A → B en el diagrama de Hasse significa que existe una manera de llegar del punto A al punto B en la ciudad. Entonces, ¿qué es un profunctor?
Un profunctor es solo un montón de puentes que conectan puntos de una ciudad con puntos de otra. Veamos un ejemplo específico. Aquí hay una imagen de un Bool -profunctor Φ: X → Y:
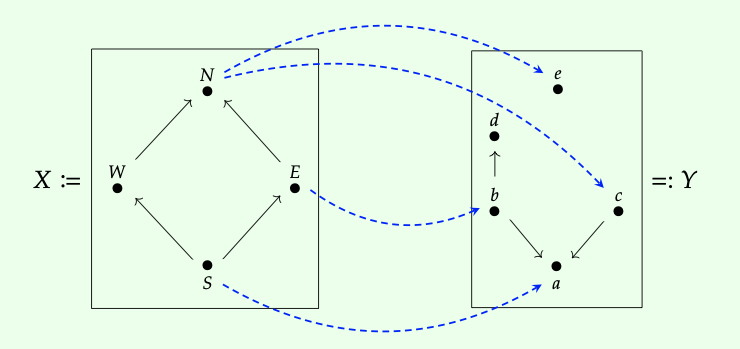
Tanto X como Y son pedidos por adelantado, por ejemplo con W ≤ N y b ≤ a. Con los puentes que vienen del profunctor en azul, ahora se pueden utilizar ambos caminos dentro de las ciudades y los puentes para llegar de puntos en la ciudad X a puntos de la ciudad Y. Por ejemplo, como hay una ruta de N a e y E a, tenemos Φ (N, e) = verdadero y Φ (E, a) = verdadero. Por otro lado, como no hay camino de W a d, tenemos Φ (W, d) = falso.
De hecho, se podría poner una caja alrededor de toda esta imagen y ver un nuevo preorden con W ≤ N ≤ c ≤ a, etc. Esto se llama el collage de Φ; exploraremos esto con más detalle más adelante; ver Definición 4.42.
Ejercicio 4.12.
Podemos expresar Φ como una matriz donde la entrada (m, n) ésima es el valor de Φ (m, n)\(\in\)\(\mathbb{B}\). Llene la matriz Bool:

A esto lo llamaremos la matriz de factibilidad de Φ.
Consideremos ahora los Profunctors de Cost. Nuevamente podemos verlos como puentes, pero esta vez nuestros puentes están etiquetados por su longitud. Recordemos de la definición 2.53 y la ecuación (2.56) que las categorías de costo son espacios métricos de Lawvere, y se pueden representar usando gráficas ponderadas. Pensaremos en una gráfica tan ponderada como una gráfica de distancias entre puntos en una ciudad, y generaremos un coste-profunctor construyendo algunos puentes entre las ciudades.
Aquí hay una representación de un Profunctor Costo Φ: X Y:
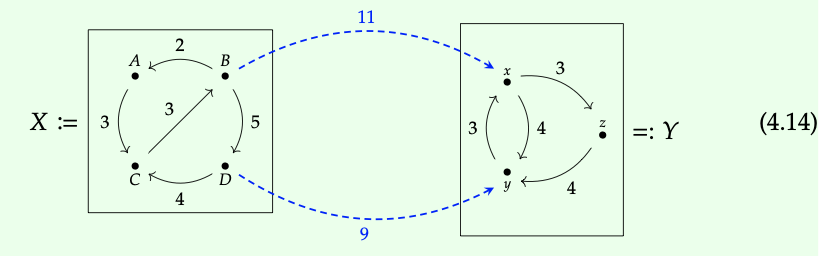
La distancia desde un punto x en la ciudad X hasta un punto y en la ciudad Y viene dada por el camino más corto que va de x a X, luego a través de uno de los puentes, y luego a través de Y hasta el destino y. Entonces, por ejemplo
Φ (B, x) = 11, Φ (A, z) = 20, Φ (C, y) = 17.
Ejercicio 4.15.
Llene la matriz Cost:

Observación 4.16 (Profunctores de cómputos vía multiplicación matricial). Podemos dar un algoritmo para calcular la matriz de distancia anterior usando multiplicación matricial. Primero, al igual que en la Ecuación (2.59), podemos comenzar con las gráficas etiquetadas en la Ecuación (4.14) y leer las matrices de etiquetas de flecha para X, Y y Φ:
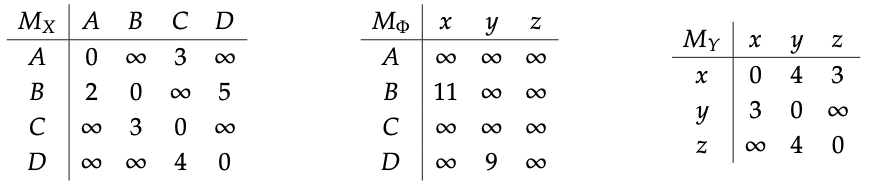
Recordemos de la Sección 2.5.3 que la matriz de distancias d Y para Costo-categoría X se puede obtener tomando la potencia matricial de M X con entradas más pequeñas, y de manera similar para Y.
La matriz de distancias para el profunctor Φ será igual a d\(_{X}\) ∗ M\(_{Φ}\) ∗ d\(_{Y}\).
De hecho, como X tiene cuatro elementos e Y tiene tres, eso también lo sabemos\(\Phi=M_{X}^{3} * M_{\Phi} * M_{Y}^{2}\).
Ejercicio 4.17.
Calcular\(\Phi=M_{X}^{3} * M_{\Phi} * M_{Y}^{2}\), recordando hacer multiplicación matricial según la fórmula (min, +) para multiplicación matricial en el Quantale Cost; ver Eq. (2.101).
Tu respuesta debe estar de acuerdo con lo que obtuviste en el Ejercicio 4.15; ¿no? ♦
Volver a diagramas de co-diseño
Cada caja en un diagrama de codiseño tiene un lado izquierdo y otro derecho, que a su vez consisten en una colección de puertos, que a su vez están etiquetados por preordenes. Por ejemplo, considere la caja del chasis a continuación:
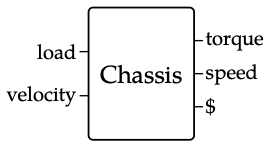
Su lado izquierdo consta de dos puertos uno para carga y otro para velocidad y estos son la funcionalidad que produce el chasis. Su lado derecho consta de tres puertos uno para par, uno para velocidad y otro para $ y estos son los recursos que requiere el chasis. Cada uno de estos recursos se debe tomar como preorden. Por ejemplo, load podría ser el preorder ([0, ∞], ≤), donde un elemento x\(\in\) [0, ∞] representa la idea “Puedo manejar cualquier carga hasta x.”, mientras que $ podría ser el preorder de dos elementos {up_to_$100, more_than_$100}, donde el primer elemento de este conjunto es menor que el segundo.
Luego multiplicamos, es decir, tomamos el preorden del producto de todos los pedidos por adelantado a la izquierda, y de manera similar para los de la derecha. El recuadro representa entonces una relación de factibilidad entre los resultados. Por ejemplo, la caja de chasis anterior representa una relación de factibilidad
Chasis: (carga × velocidad) → (par × velocidad × $)
Vamos a recorrer esto un poco más concretamente. Considera el problema de diseño de filmar una película, donde debes enfrentar el tono y el valor del entretenimiento contra el costo.
Una relación de factibilidad que describe esta situación detalla qué tono y valor de entretenimiento se puede obtener a cada costo; como tal, se describe mediante una relación de factibilidad Φ: (T × E) → $. Representamos esto por la caja
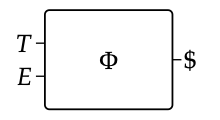
donde T, E y $ son los pedidos por adelantado dibujados a continuación:
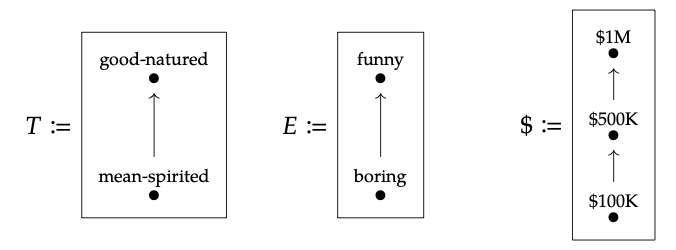
Luego, el profunctor describe una posible relación de factibilidad
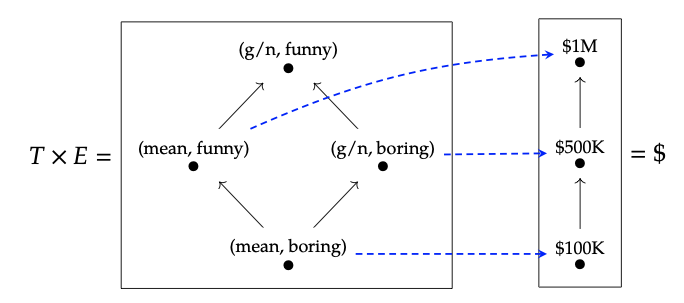
Esto dice, por ejemplo, que una película bondadosa pero aburrida cuesta 500K para producir (por supuesto, los productores también estarían felices de obtener un millón de dólares).
Para elaborar, cada flecha en el diagrama anterior debe interpretarse como diciendo: “Puedo proporcionar la fuente dada la diana”. Por ejemplo, hay flechas presenciando cada uno de “Puedo proporcionar $500K dado $1M”, “Puedo proporcionar una película bondadosa pero aburrida dada $500K”, y “Puedo proporcionar una película mala y aburrida dada una película bondadosa pero aburrida”. Además, esta relación es transitiva, por lo que el camino de (media, aburrida) a $1M indica también que “puedo proporcionar una película media y aburrida dada $1M”.
Observe la similitud y diferencia con la interpretación puente de los profunctores en el Ejemplo 4.11: las flechas aún indican la posibilidad de moverse entre la fuente y el objetivo, pero en esta interpretación impulsada por el co-diseño las entendemos como indicativas de que es posible llegar a la fuente del objetivo.
En el diagrama anterior, el nodo (g/n, gracioso) no tiene una flecha azul discontinua emergiendo de él. ¿Esto es válido? Si es así, ¿qué significa? ♦


