7.1: ¿Cómo podemos probar que nuestra máquina es segura?

Imagina que estás tratando de diseñar un sistema de componentes que interactúen. No estarías haciendo esto si no tuvieras un objetivo en mente: quieres que el sistema haga algo, que se comporte de cierta manera. En otras palabras, quieres restringir sus posibilidades a un conjunto más pequeño: quieres que el auto permanezca en la carretera, quieres que la temperatura permanezca en un rango particular, quieres que el puente sea seguro para que pasen los camiones. De todas las posibilidades, tu sistema solo debería permitir algunas.

Dado que su sistema está hecho de componentes que interactúan de formas específicas, el posible comportamiento del conjunto en cualquier entorno está determinado por los posibles comportamientos de cada uno de sus componentes en sus entornos locales, junto con la forma precisa en que interactúan.1 En este capítulo, discutiremos un lógica en la que se pueden describir los tipos generales de comportamiento que ocurren a lo largo del tiempo, y probar las propiedades de un sistema a mayor escala a partir de las propiedades y patrones de interacción de sus componentes.

Por ejemplo, supongamos que queremos que un vehículo autónomo mantenga una distancia de algunos\(\in\)\(\mathbb{R}\) a salvo de otros objetos. Para ello, varios componentes deben interactuar: un sensor que se aproxime a la distancia real por una variable interna S′, un controlador que usa S′ para decidir qué acción A tomar, y un motor que mueve el vehículo con una aceleración basada en A. Esto a su vez afecta la distancia real S, por lo que hay un bucle de retroalimentación.

Considere el siguiente diagrama de modelo:

En el diagrama mostrado, la distancia S es expuesta por la interfaz exterior. Esto solo significa que imaginamos que S es una variable con la que otros componentes de un sistema más grande pueden querer interactuar. Podríamos haber expuesto ninguna variable (convirtiéndolo en un sistema cerrado) o podríamos haber expuesto A y/o S′ también.

Para que el sistema garantice S ≥ seguro, necesitamos que cada uno de los componentes asegure una propiedad propia. Pero, ¿qué son estos componentes, 'sensor, controlador, motor', y qué hacen?

Una forma de pensar en cualquiera de los componentes es abrirla y ver cómo se articula; con un estudio detallado podemos decir qué va a hacer. Por ejemplo, así como se expuso S en el diagrama anterior, uno podría imaginar abrir la caja de componentes 'sensor' en la ecuación (7.1) y ver una interacción entre subcomponentes

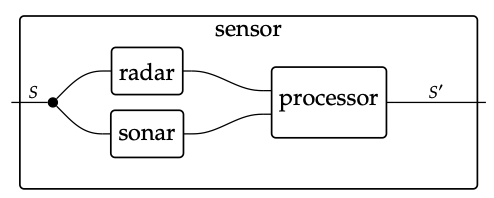
Esta capacidad de acercar y ver una sola unidad como compuesta por otras es importante para el diseño. Pero al final del día, eventualmente necesitas dejar de bucear y simplemente usar las propiedades de los componentes frente a ti para probar propiedades del sistema compuesto. No tengas miedo: todo lo que hagamos en este capítulo será completamente compositivo, es decir, compatible con la apertura de subsistemas de nivel inferior y el uso de la naturaleza fractal de la composición. Sin embargo, en un momento dado, su trabajo es diseñar el sistema a un nivel determinado, tomando las propiedades de los componentes de los sistemas de nivel inferior como se dan.

Pensaremos en cada componente en términos de la relación que mantiene (a través del tiempo) entre los valores cambiantes en sus puertos. “Siempre que vea un destello, aumentaré la presión sobre el botón”: esta es una relación que mantengo a través del tiempo entre los valores cambiantes en mi puerto ocular y el puerto de mi dedo. Pronto lo haremos más preciso, pero desarrollar la situación en la Ecuación (7.1) debería ayudar. El sensor mantiene una relación entre S y S', por ejemplo, que la distancia real S y su representación interna S' difieren en no más de 5cm. El controlador mantiene una relación entre S' y la señal de acción A, por ejemplo, que si en algún momento S < seguro, entonces dentro de un segundo emitirá la señal A = go. El motor mantiene una relación entre A y S, por ejemplo, que A dicta la segunda derivada de S por la fórmula

\(((A=\mathrm{go}) \Rightarrow \ddot{S}>1) \wedge((A=\mathrm{stop}) \Rightarrow \ddot{S}=0)\)(7.2)

Si queremos probar propiedades de todo el sistema de interacción, entonces las relaciones- naves mantenidas por cada componente necesitan ser escritas en un lenguaje lógico formal, algo así como lo que vimos en la Ec. (7.2). A partir de esa base, podemos utilizar técnicas de prueba estándar para combinar propiedades de subsistemas en propiedades del conjunto. Este es nuestro objetivo en el presente capítulo.

Hemos dicho cómo los sistemas de componentes, cableados juntos en algún arreglo, crean sistemas a mayor escala. También hemos dicho que, dada la disposición del cableado, las propiedades de ser conductuales de los sistemas componentes dictan las propiedades conductuales del conjunto. Pero, ¿qué son exactamente las propiedades conductuales?

En este capítulo, queremos dar un lenguaje formal y semántica para una noción muy genérica de comportamiento. Las matemáticas son en sí mismas un lenguaje formal; el estilo habitual del modelado matemático es utilizar cualquier pieza de este vasto lenguaje en cualquier momento y por cualquier motivo. Se utiliza la “comprensión humana” para asegurar que los diferentes modelos se ajusten de manera apropiada cuando se combinan diferentes sistemas. El presente trabajo difiere en que queremos encontrar un lenguaje específico de dominio para modelar el comportamiento, cualquier tipo de comportamiento y nada más que comportamiento. A diferencia del amplio mundo de las matemáticas, queremos un entorno donde lo único que se pueda discutir sean los comportamientos.

Para ello, construiremos lo que se llama un topos, que es un tipo especial de categoría. Nuestros topos, llamémoslo BT, tendrán tipos de comportamiento en términos generales, conjuntos cuyos elementos pueden cambiar a través del tiempo, como sus objetos. Un dato sorprendente sobre los toposes2 es que vienen con un lenguaje interno que se parece mucho al lenguaje formal habitual de las matemáticas en sí. Así se pueden definir gráficas, grupos, espacios topológicos, etc. en cualquier topo. Pero en BT, lo que llamamos gráficos en realidad serán gráficos que cambian a través del tiempo, y de manera similar lo que llamamos grupos y espacios en realidad serán grupos y espacios que cambian a través del tiempo.

El topos BT no sólo tiene un lenguaje interno, sino también una semántica matemática utilizando la noción de gavillas. Técnicamente, una gavilla es un cierto tipo de functor, pero uno puede imaginarlo como un espacio de posibilidades, variando de manera controlada; en nuestro caso será un espacio de posibles comportamientos que varían en una determinada noción de tiempo. Cada propiedad que probemos en nuestra lógica de tipos de comportamiento tendrá significado en esta categoría de poleas.

Al hablar de sistemas y componentes, como sensores, controladores, motores, etc., mencionamos los tipos de comportamiento; estos serán los objetos en los topos BT. Cada cable en la imagen siguiente representará un tipo de comportamiento, y cada casilla X representará una propiedad de comportamiento, una relación que X mantiene entre los valores cambiantes en sus puertos.

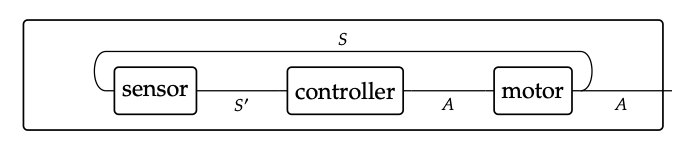
Por ejemplo podríamos imaginar que

• S (cable): El comportamiento de S a lo largo de un intervalo de tiempo [a, b] es el de todas las funciones continuas de valor real [a, b] →\(\mathbb{R}\).

• A (cable): El comportamiento de A a lo largo de un intervalo de tiempo [a, b] son todas las funciones constantes por partes, tomando valores en el conjunto finito como {go, stop}.

• controlador (caja): la relación {(S ′, A) | Eq. (7.2)}, es decir, todos los pares de comportamiento (S ′, A) que se ajustan a lo que dijimos que nuestro controlador se supone que debe hacer en la Ec. (7.2).