7.2: El Conjunto de Categorías como Topos Ejemplares

Última actualización
Guardar como PDF

Page ID: 112351

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Queremos pensar en una especie de cosas muy abstractas, llamadas topos, porque veremos que los tipos de comportamiento forman un topos. Para comenzar, comenzamos con uno de los toposes más fáciles de pensar, a saber, el Conjunto de conjuntos de topos. En esta sección discutiremos los puntos en común entre conjuntos y todos los demás topos. Entraremos en algunos detalles sobre la categoría de conjuntos, para dar intuición para otros toposes. En particular, vamos a prestar especial atención a la lógica de los conjuntos, porque finalmente queremos entender la lógica de los comportamientos.

En efecto, la lógica y los conjuntos están estrechamente relacionados. Por ejemplo, la afirmación lógica más formalmente conocida como predicado likes_cats define una función desde el conjunto P de personas hasta el conjunto$\mathbb{B}$ = {falso, verdadero} de valores de verdad, donde Brendan$\in$ P mapea a true porque le gustan los gatos mientras que Úrsula$\in$ P mapas a falso porque no lo hace. Alternativamente, likes_cats también define un subconjunto de P, que consiste exactamente en las personas a las que les gustan los gatos

{p$\in$ P | gustos_gatos (p)}.

En términos de estos subconjuntos, las operaciones lógicas corresponden a operaciones de conjunto, por ejemplo Y corresponde a intersección: de hecho, el conjunto de personas para (mapeado a verdadero por) el predicado Likes_cats_and_likes_dogs es igual a la intersección del conjunto para likes_cats y el conjunto para likes_dogs.

Vimos en el Capítulo 3 que tales operaciones, que son ejemplos de consultas de bases de datos, pueden describirse en términos de límites y corlímites en Set. En efecto, la categoría Set tiene muchas estructuras y propiedades de este tipo, que en conjunto hacen posible la lógica en ese entorno. En esta sección queremos identificar estas propiedades, y mostrar cómo se pueden definir las operaciones lógicas usándolas.

¿Por qué querríamos encontrar abstractamente tales estructuras y propiedades? En la siguiente sección, iniciaremos nuestra búsqueda de otras categorías que también las tengan. Dichas categorías, llamadas toposes, serán Set como suficiente para hacer lógica, pero tienen una semántica mucho más compleja e interesante. En efecto, discutiremos uno cuya lógica nos permita razonar no sobre las propiedades de los conjuntos, sino sobre las propiedades de comportamiento de máquinas muy generales.

Propiedades tipo conjunto disfrutadas por cualquier topos

Aunque no lo probaremos en este libro, los toposes son categorías que son similares a Set en muchos sentidos. Aquí hay algunos datos que son ciertos de cualquier topos$\mathcal{E}$:

$\mathcal{E}$tiene todos los límites,
$\mathcal{E}$tiene todos los colímites,
$\mathcal{E}$está cerrado cartesiano,
$\mathcal{E}$tiene factorizaciones epi-mono,
$\mathcal{E} \text { has a subobject classifier } 1 \stackrel{\text { true }}{\longrightarrow} \Omega \text { . }$

En particular, dado que Set es un topos, todos los hechos anteriores son ciertos para$\mathcal{E}$ = Set. Nuestro primer objetivo es revisar brevemente estos conceptos, enfocándonos más en el clasificador de subobjeto.

Límites y corlímites. Hablamos brevemente de límites y corlímites en la Sección 3.4.2, pero la idea básica es que se pueden hacer nuevos objetos a partir de viejos tomando productos, usando ecuaciones para definir subobjetos, formando uniones disjuntas y tomando cocientes.object 0. Uno de los tipos de límite más importantes (resp. colimit) es el de los retrocesos (resp. pushouts); ver Ejemplo 3.99 y Definición 6.19. Para nuestro trabajo a continuación, necesitaremos saber un toque más sobre los retrocesos de lo que hemos comentado hasta ahora, así que comencemos por ahí.

Supongamos que C es una categoría y considera los diagramas a continuación:

$Screen Shot 2021-01-25 at 1.56.43 PM.png$

En el cuadrado izquierdo, el símbolo de esquina significa$\text { I }$ inequívocamente que el cuadrado (B, C, E, F) es un retroceso. Pero en el cuadrado derecho, ¿significa el símbolo de esquina que (A, B, D, E) es un retroceso o que (A, C, D, F) es un retroceso? Es ambiguo, pero como mostramos a continuación, se vuelve inequívoco si el cuadrado de la derecha es un retroceso.

Proposición 7.3.

En el diagrama conmutativo a continuación, supongamos que el cuadrado (B, C, B′, C′) es un retroceso:

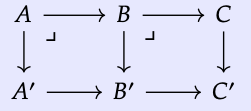
$Screen Shot 2021-01-25 at 1.57.45 PM.png$

Entonces el cuadrado (A, B, A′, B′) es un retroceso si el rectángulo (A, C, A′, C′) es un retroceso.

Ejercicio 7.4.

Probar la Proposición 7.3 utilizando la definición de límite de la Sección 3.4.2. ♦

Factorizaciones Epi-mono. La abreviatura 'epi' significa epimorfismo, y la ab- breviación 'mono' significa monomorfismo. Los epimorfismos son mapas que actúan como suryecciones, y los monomorfismos son mapas que actúan como inyecciones. $^{3}$Podemos definirlos formalmente en términos de flexiones y retrocesos.

Definición 7.5.

Que C sea una categoría, y que f: A → B sea un morfismo. Se llama monomorfismo (resp. epimorfismo) si el cuadrado a la izquierda es un retroceso (resp. el cuadrado a la derecha es un pushout):

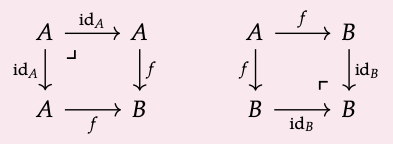
$Screen Shot 2021-01-25 a las 2.12.15 PM.png$

Ejercicio 7.6.

Demuestre que en Set, los monomorfismos son solo inyecciones:

1. Demostrar que si f es un monomorfismo entonces es inyectivo.
2. Demostrar que si f: A → B es inyectable entonces es un monomorfismo. ♦

Ejercicio 7.7.

1. Demostrar que el retroceso de un isomorfismo a lo largo de cualquier morfismo es un isomorfismo. Es decir, supongamos que i: B ′ → B es un isomorfismo y f: A → B es cualquier morfismo. Demostrar que i ′ es un isomorfismo, en el siguiente diagrama:

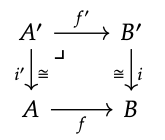
$Screen Shot 2021-01-25 a las 2.15.29 PM.png$

2. Mostrar que para cualquier mapa f: A → B, el cuadrado que se muestra es un retroceso:

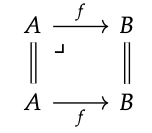$Screen Shot 2021-01-25 a las 2.16.23 PM.png$ ♦

Ejercicio 7.8.

Supongamos que el siguiente diagrama es un retroceso en una categoría C:

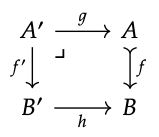
$Screen Shot 2021-01-25 a las 2.18.10 PM.png$

Usa la Proposición 7.3 y el Ejercicio 7.7 para mostrar que si f es un monomorfismo, entonces también lo es f ′ . ♦

Ahora que hemos definido epimorfismos y monomorfismos, podemos decir qué son las factorizaciones epi-mono. Decimos que un morfismo f: C → D en E tiene una factorización epi-mono si tiene una 'imagen'; es decir, hay un objeto im (f), un epimorfismo C$\twoheadrightarrow$ im (f), y un monomorfismo im (f)$\rightarrowtail$ D , cuyo compuesto es f.

En Set, los epimorfismos son suryecciones y los monomorfismos son inyecciones.

Cada función f: C → D puede ser factorizada como una función suryectiva sobre su imagen im (f) = {f (c) | $\in$c C}, seguida de la inclusión de esta imagen en el codominio D. Además, esta factorización es única hasta el isomorfismo.

Ejercicio 7.9.

Factorizar la siguiente función f: 3 → 3 como epimorfismo seguido de un monomorfismo.

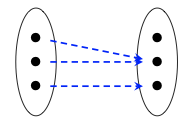$Screen Shot 2021-01-25 a las 2.19.45 PM.png$ ♦

Este es el caso en cualquier topos$\mathcal{E}$: para cualquier morfismo f: c → d, existe un epimorfismo e y un monomorfismo m tal que f = (e; m) es su compuesto.

Cartesiano cerrado. Una categoría C que es cartesiana cerrada significa que C tiene una estructura monoidal simétrica dada por los productos, y es monoidal cerrada con respecto a esto. (Anteriormente vimos el cierre monoidal en la Definición 2.79 (para preórdenes) y en la Proposición 4.60, como corolario del cierre compacto.) Un poco más realista, el cierre cartesiano significa que para dos objetos C, D$\in$ C, hay un 'hom-object' D$^{C}$ $\in$C y un isomorfismo natural para cualquier A$\in$ C:

C (A × C, D)$\cong$ C (A, D$^{C}$) (7.10)

Piénsalo de esta manera. Supongamos que eres A y yo soy C, y estamos interactuando a través de algún juego f (−, −): A × C → D: para cualquier acción a $\in$A que tomes y acción c$\in$ C que yo take, f (a, c) es algún valor en D. Como eres egocéntrico pero amoroso, piensas en esta situación como si estuvieras creando una experiencia de juego para mí. Cuando haces a, haces un juego f (a, −): C → D solo para mí. En el formalismo, D$^{C}$ representa el conjunto de juegos para mí. Entonces ahora has transformado un juego para dos jugadores, valorado en D, en un juego de un jugador, eres el jugador, valorado en... juegos de un jugador valorados en D. Esta transformación es invertible puedes cambiar tu punto de vista a voluntad y se llama currying. Este es el contenido del Ejemplo 3.72.

Ejercicio 7.11.

Sea V = (V, ≤, I,) a (unital, conmutativo) quantale ver Definición 2.90 y supongamos que satisface lo siguiente para todos v, w, x$\in$ V:

• v ≤ I,

• v w ≤ v y v w ≤ w, y

• si x ≤ v y x ≤ w entonces x ≤ v w.

1. Mostrar que V es una categoría cerrada cartesiana, de hecho una preorden cerrada cartesiana.

2. ¿Se puede obtener de esta manera todos los prepedidos cartesianos cerrados? ♦

Clasificador de subobjectos. El concepto de clasificador subobjeto requiere más atención, porque su existencia tiene enormes consecuencias para una categoría C. En particular, crea el escenario para que exista un rico sistema de lógica de orden superior dentro de C; lo hace aportando algunas cosas llamadas 'valores de verdad'. La lógica de orden superior se manifiesta en su plena gloria cuando C tiene límites finitos y es cartesiano cerrado, porque estos hechos dan lugar a las operaciones lógicas sobre los valores de la verdad.4 En particular, la lógica de orden superior existe en cualquier topos.

Vamos a explicar los clasificadores de subobjeto con el mayor detalle que podamos; de hecho, será nuestro tema para el resto de la Sección 7.2.

El clasificador de subobjectos

Antes de dar la definición de clasificadores subobjetos, recordemos que los monomorfismos en Set son inyecciones, y cualquier inyección X$\rightarrowtail$ Y es isomórfica a un subconjunto de Y. Esto da una manera simple y útil de conceptualizar monomorfismos en Y al leer la siguiente definición: no hará daño pensar en ellos como subobjetos de Y.

Definición 7.12.

Dejar$\mathcal{E}$ ser una categoría con límites finitos, es decir, con retrocesos y un objeto ter- minal 1. Un clasificador de subobjeto en$\mathcal{E}$ consiste en un objeto Ω$\in$$\mathcal{E}$, junto con un monomorfismo verdadero: 1 → Ω, satisfaciendo la siguiente propiedad: para cualquier objeto X e Y y monomorfismo m: X$\rightarrowtail$ Y en $\mathcal{E}$, hay un morfismo único$\lceil{m}\rceil$: Y → Ω tal que el diagrama a la izquierda de la Ec. (7.13) es un retroceso en$\mathcal{E}$:

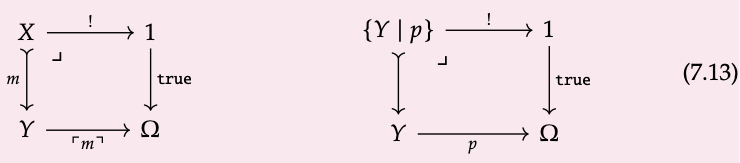
$Screen Shot 2021-01-25 en 2.40.17 PM.png$

Nos referimos$\lceil{m}\rceil$ como el mapa característico de$\lceil{m}\rceil$, o decimos que m clasifica$\lceil{m}\rceil$. Por el contrario, dado cualquier mapa p: Y → Ω, denotamos el retroceso de true como a la derecha de la Ec. (7.13).

Un predicado sobre Y es un morfismo Y → Ω.

Definición 7.12 es un poco difícil de entender, en parte porque es difícil imaginar sus consecuencias. Es como una pepita superdensa del espacio exterior, y a través de exploraciones científicas en la segunda mitad del siglo XX, hemos encontrado que aporta superpoderes a las categorías que la posean. Vamos a explicar algunas de las consecuencias a continuación, pero muy rápidamente, la idea es la siguiente.

Cuando una categoría tiene un clasificador de subobjetos, proporciona un traductor, convirtiendo subobjetos de cualquier objeto Y en mapas de ese Y al objeto particular Ω. Pullback del monomorfismo true: 1 → Ω proporciona un traductor retrocediendo, convirtiendo los mapas Y → Ω en subobjetos de Y. Podemos reemplazar nuestra fantasía de la pepita superdensa por una historia un poco más refinada: “cualquier objeto Y se entiende a sí mismo, sus partes y la lógica de cómo encajan, haciendo preguntas al oráculo Ω, buscando lo que es verdad”. O para ser completamente precisos pero secos, “los subobjetos de Y se clasifican por predicados sobre Y”.

Pasemos de historias y consignas a hechos concretos.

El clasificador de subobjeto en Set. Dado que Set es un topos, tiene un clasificador subobjeto. Será un conjunto con propiedades supuestamente maravillosas; ¿qué conjunto es?

El clasificador de subobjeto en Set es el conjunto de booleanos,

Ω$_{Set}$ :=$\mathbb{B}$ = {verdadero, falso} . (7.14)

Entonces en Set, los valores de verdad son verdaderos y falsos.

Por definición (Def. 7.12), el clasificador subobjeto viene equipado con un morfismo, genéricamente llamado true: 1 → Ω; en el caso de Set es jugado por la función 1 → {true, false} que envía 1 a true. En otras palabras, el morfismo verdadero se nombra acertadamente en este caso.

Para los sets, monomorfismo solo significa inyección, como mencionamos anteriormente. Entonces Defini- tion 7.12 dice que para cualquier función inyectiva m: X$\rightarrowtail$ Y entre conjuntos, se supone que podemos encontrar una función característica$\lceil{m}\rceil$: Y → {true, false} con algún tipo de propiedad pullback.

Proponemos la siguiente definición de$\lceil{m}\rceil$:

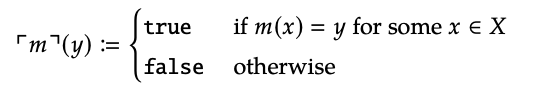
$Screen Shot 2021-01-25 en 2.55.41 PM.png$

En otras palabras, si pensamos en X como un subobjeto de Y, entonces hacemos$\lceil{m}\rceil$ (y) igual a verdadero iff y$\in$ X.

En particular, la propiedad del clasificador de subobjetos convierte los subconjuntos X$\subseteq$ Y en funciones p: Y →$\mathbb{B}$, y viceversa.

Cómo funciona está codificado en la Definición 7.12, pero la idea básica es que X será el conjunto de todas las cosas en Y que p envía a true:

X = {y$\in$ Y | p (y) = verdadero} . (7.15)

Esto podría ayudar a explicar nuestra notación abstracta {Y | p} en la Ec. (7.13).

Ejercicio 7.16.

Sea X =$\mathbb{N}$ = {0, 1, 2,...} e Y =$\mathbb{Z}$ = {..., −1, 0, 1, 2, ... };

tenemos X$\subseteq$ Y, así que considérelo como un monomorfismo m: X$\rightarrowtail$ Y.

Tiene una función característica$\lceil{m}\rceil$: Y →$\mathbb{B}$, como en la Definición 7.12.

1. ¿Qué es$\lceil{m}\rceil$ (−5)$\in$$\mathbb{B}$?

2. ¿Qué es$\lceil{m}\rceil$ (0)$\in$$\mathbb{B}$? ♦

Ejercicio 7.17.

1. Considere la función de identidad id$_{\mathbb{N}}$:$\mathbb{N}$ →$\mathbb{N}$.

Se trata de una inyección, por lo que tiene una función característica id$\lceil{_{\mathbb{N}}}\rceil$:$\mathbb{N}$ →$\mathbb{B}$.

Dar una descripción concreta de id$\lceil{_{\mathbb{N}}}\rceil$, es decir, su valor exacto para cada número natural n$\in$$\mathbb{N}$.

2. ¡Considera la función única! $_{\mathbb{N}}$: Ø → N del juego vacío. Dar una descripción concreta de$\lceil{!_{\mathbb{N}}}\rceil$:$\mathbb{N}$ →$\mathbb{B}$. ♦

Lógica en el conjunto de topos

Como dijimos anteriormente, el clasificador subobjeto de cualquier topos$\mathcal{E}$ da el ajuste en el que hacer lógica. Antes de explicar un poco sobre cómo funciona la lógica de topos en general, seguimos trabajando concretamente centrándonos en la lógica en el conjunto de topos.

Obtención de la operación AND. Considera la función 1 →$\mathbb{B}$ ×$\mathbb{B}$ escogiendo el elemento (true, true). Esto es un monomorfismo, por lo que define una función característica$\lceil{(true, true)}\rceil$:$\mathbb{B}$ ×$\mathbb{B}$ →$\mathbb{B}$. ¿Qué función es? Por la Ec. (7.15) el único elemento de$\mathbb{B}$ ×$\mathbb{B}$ que se puede enviar a true es (true, true). Así$\lceil{(true, true)}\rceil$ (P, Q)$\in$$\mathbb{B}$ debe ser dado por la siguiente tabla de verdad

$Screen Shot 2021-01-25 at 3.38.32 PM.png$

Esta es exactamente la tabla de verdad para el AND de P y Q, es decir, para P$\bigwedge$ Q. En otras palabras,$\lceil{(true, true)}\rceil$ =$\bigwedge$.

Tenga en cuenta que esto define$\bigwedge$ como una función$\bigwedge$:$\mathbb{B}$ ×$\mathbb{B}$ →$\mathbb{B}$, y usamos la notación de infijo habitual x$\bigwedge$ y: =$\bigwedge$ (x, y).

Obtención de la operación OR. Vamos a retroceder esta vez.

La tabla de verdad para el OR de P y Q, es decir, la de la función$\bigvee$:$\mathbb{B}$ ×$\mathbb{B}$ →$\mathbb{B}$ definiendo OR, es:

$Screen Shot 2021-01-25 a las 4.10.21 PM.png$

Si quisiéramos obtener esta función como la función característica$\lceil{m}\rceil$ de algún subconjunto m: X$\subseteq$$\mathbb{B}$ ×$\mathbb{B}$, ¿qué subconjunto sería X? Por la Ec. (7.15), X debe ser el conjunto de$\in$ y Y que se envían a true. Así, m es el mapa característico para el subconjunto de tres elementos

X = {(verdadero, verdadero), (verdadero, falso), (falso, verdadero)}$\subseteq$$\mathbb{B}$ ×$\mathbb{B}$.

Para prepararnos para una posterior generalización de esta idea en cualquier topos, queremos una forma de pensar de X solo en términos de propiedades listadas al inicio de la Sección 7.2.1. De hecho, se puede pensar en X como la unión de {true} ×$\mathbb{B}$ y$\mathbb{B}$ × {true} un colímite de límites que involucra al clasificador subobjeto y al objeto terminal. Esta descripción construirá un subobjeto análogo de Ω × Ω, y por lo tanto clasificará un mapa Ω × Ω → Ω, en cualquier topos$\mathcal{E}$.

Ejercicio 7.19.

Cada booleano tiene una negación, ¬false = true y ¬true = false. La función ¬:$\mathbb{B}$ →$\mathbb{B}$ es la función característica de alguna cosa, (*? *).

¿Qué tipo de cosas deberían (*? *) ser? Por ejemplo, ¿debería ¬ ser la función característica de un objeto? ¿Un topos? ¿Un morfismo? ¿Un subobjeto? ¿Un diagrama de retroceso?
Ahora que ya sabes el tipo de cosas (*? *) es, ¿qué cosa de ese tipo es? ♦

Ejercicio 7.20.

Dados dos booleanos P, Q, definen P ⇒ Q para significar P = (P$\bigwedge$ Q).

1. Anote la tabla de verdad para la sentencia P = (P$\bigwedge$ Q):

$Screen Shot 2021-01-25 a las 4.26.36 PM.png$

Si ya tienes idea de lo que debería significar P ⇒ Q, ¿está de acuerdo con la última columna de la tabla anterior?
¿Cuál es la función característica m:$\mathbb{B}$ ×$\mathbb{B}$ →$\mathbb{B}$ para P ⇒ Q?
¿Qué subobjecto clasifica m? ♦

Ejercicio 7.21.

Considera los conjuntos E: = {n$\in$$\mathbb{N}$ | n es par}, P: = {n$\in$$\mathbb{N}$ | n es primo}, y T := {n$\in$$\mathbb{N}$ | n ≥ 10}. Cada uno es un subconjunto de N, así define una función N → B.

1. ¿Qué es$\lceil{E}\rceil$ (17)?

2. ¿Qué es$\lceil{P}\rceil$ (17)?

3. ¿Qué es$\lceil{T}\rceil$ (17)?

4. Nombra los tres elementos más pequeños del conjunto clasificados por ($\lceil{E}\rceil$$\bigwedge$$\lceil{P}\rceil$)$\bigvee$$\lceil{T}\rceil$. ♦

Revisión. Hagamos un balance de dónde estamos y hacia dónde vamos. En la Sección 7.1, establecemos nuestro objetivo de probar propiedades sobre el comportamiento, y dijimos que la teoría de topos es un buen escenario matemático para hacerlo. Ahora estamos al final de la Sección 7.2, que se trataba de Establecer como un ejemplo de topos. ¿Qué pasó?

En la Sección 7.2.1, hablamos sobre las propiedades de Set que disfrutan todos los topos: límites y corlímites, cierre cartesiano, factorizaciones epi-mono y clasificadores de subobjeto. Entonces en la Sección 7.2.2 nos lanzamos a pensar en el clasificador subobjeto en general y en el conjunto de topos específico, donde es el conjunto$\mathbb{B}$ de booleanos porque cualquier subconjunto de Y es clasificado por un predicado específico p: Y →$\mathbb{B}$. Por último, en la Sección 7.2.3 discutimos cómo entender la lógica en términos de Ω: hay varios mapas$\bigwedge$$\bigvee$,, ⇒: Ω × Ω → Ω y ¬: Ω → Ω etc., que sirven como conectivos lógicos. Se trata de operaciones sobre valores de verdad.

Hemos hablado mucho de toposes, pero hasta ahora sólo hemos visto uno: la categoría de conjuntos. Pero en realidad hemos visto más sin saberlo: la categoría C- Inst de instancias en cualquier esquema de base de datos de Definición 3.60 es un topos. Tales toposes se llaman toposes presheaf y son fundamentales, pero nos enfocaremos en toposes de gavillas, porque nuestros topos de tipos de comportamiento serán topos de gavilla. Las poleas son fascinantes, pero objetos matemáticos altamente abstractos. No son para los débiles de corazón matemático (los que son débiles de corazón físico son bienvenidos a proceder).