4.1: Facciones de números enteros

Última actualización
Guardar como PDF

Page ID: 116736

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

entender el concepto de fracciones de números enteros
ser capaz de reconocer las partes de una fracción

Más números en la línea numérica

En los Capítulos [link], [link], y [link], estudiamos los números enteros y los métodos para combinarlos. Señalamos que podíamos mostrar visualmente los números enteros dibujando una línea numérica y colocando círculos cerrados en ubicaciones de números enteros.

$Una línea numérica con puntos en los números enteros.$

Al observar esta recta numérica, podemos ver que los números enteros no dan cuenta de cada punto de la línea. ¿Qué números, si los hay, se pueden asociar a estos puntos? En esta sección veremos que muchos de los puntos en la recta numérica, incluyendo los puntos ya asociados a números enteros, pueden asociarse con números llamados fracciones.

Fracciones de números enteros

La naturaleza de las fracciones positivas
Podemos ampliar nuestra colección de números, que ahora contiene sólo los números enteros, al incluir fracciones de números enteros. Podemos determinar la naturaleza de estas fracciones usando la recta numérica.

Si colocamos un lápiz en algún número entero y procedemos a viajar a la derecha al siguiente número entero, vemos que nuestro viaje puede dividirse en diferentes tipos de partes iguales como se muestra en los siguientes ejemplos.

1 parte.
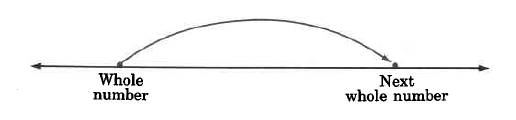
$Una línea numérica. Dos marcas: una a la izquierda, etiquetada, número entero y otra a la derecha, etiquetada con el siguiente número entero. Se dibuja una flecha desde el número entero hasta el siguiente número entero.$
2 partes iguales.
$Una línea numérica. Dos marcas: una a la izquierda, etiquetada, número entero y otra a la derecha, etiquetada con el siguiente número entero. Entre las dos marcas está el punto medio. Se dibuja una flecha desde el número entero hasta el punto medio, y luego desde el punto medio hasta el siguiente número entero.$
3 partes iguales.
$Una línea numérica. Dos marcas: una a la izquierda, etiquetada, número entero y otra a la derecha, etiquetada con el siguiente número entero. Hay tres flechas, que conectan los dos números enteros y dos marcas hash uniformemente espaciadas entre los números enteros.$
4 partes iguales.
$Una línea numérica. Dos marcas: una a la izquierda, etiquetada, número entero y otra a la derecha, etiquetada con el siguiente número entero. Hay cuatro flechas, que conectan los dos números enteros y tres marcas hash uniformemente espaciadas entre los números enteros.$

El vocablo latino Fractio

Observe que el número de piezas, 2, 3 y 4, en las que estamos dividiendo la cantidad original es siempre un número entero distinto de cero. La idea de romper una cantidad entera nos da la palabra fracción. La palabra fracción proviene del vocablo latino “fractio” que significa una rotura, o fractura.

Supongamos que dividimos el intervalo de algún número entero al siguiente número entero en cinco partes iguales.

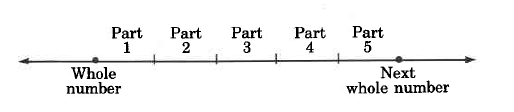
$Una línea numérica. Dos marcas: una a la izquierda, etiquetada con número entero y otra a la derecha, etiquetada con el siguiente número entero. Hay cuatro marcas hash entre los dos números enteros, creando cinco espacios de igual ancho, etiquetados Parte 1 a Parte 5.$

Después de comenzar a pasar de un número entero al siguiente, decidimos detenernos después de cubrir solo dos partes. Hemos cubierto 2 partes de 5 partes iguales. Esta situación se describe por escrito$\dfrac{2}{5}$.

$Una línea numérica. Dos marcas: una a la izquierda, etiquetada con número entero y otra a la derecha, etiquetada con el siguiente número entero. Hay cuatro marcas hash uniformemente espaciadas entre las dos marcas. Hay una flecha desde el número entero hasta la primera marca hash, y una flecha desde la primera marca hash hasta la segunda marca hash.$

Definición: Fracción positiva

Un número como$\dfrac{2}{5}$ se llama fracción positiva, o más simplemente, fracción.

Las Partes de una Fracción

Una fracción tiene tres partes.

La barra de fracción -.

Barra de fracciones
La barra de fracciones sirve como símbolo de agrupación. Separa una cantidad en grupos individuales. Estos grupos tienen nombres, como se señala en 2 y 3 a continuación.
El número distinto de cero por debajo de la barra de fracciones.

Denominador
Este número se llama denominador de la fracción, e indica el número de partes en las que se ha dividido la cantidad total. Observe que el denominador debe ser un número entero distinto de cero ya que el menor número de partes que puede tener cualquier cantidad es uno.
El número por encima de la barra de fracciones.

Numerador
Este número se llama el numerador de la fracción, e indica cuántas de las partes especificadas se están considerando. Observe que el numerador puede ser cualquier número entero (incluyendo cero) ya que se puede considerar cualquier número de las partes especificadas.
$\dfrac{\text{whole number}}{\text{nonzero whole number}} \leftrightarrow \dfrac{\text{numerator}}{\text{denominator}}$

Conjunto de Muestras A

Los diagramas en los siguientes problemas son ilustraciones de fracciones.

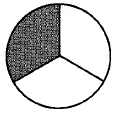
Diagramas: $Todo un círculo.$ $Un círculo entero dividido en 3 partes iguales.$ $Un círculo entero dividido en 3 partes iguales. Una de las partes está sombreada.$
1a: Un círculo entero 1b: Todo el círculo dividido en 3 partes iguales 1c: 1 de las 3 iguales partes

Figura 1.

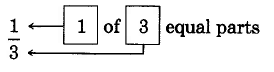
$La fracción de un tercio. Esto se leería, 1 de 3 partes iguales.$

La fracción$\dfrac{1}{3}$ se lee como “un tercio”.

Conjunto de Muestras A

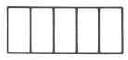
Diagramas: $Un rectángulo.$ $Un rectángulo dividido en cinco partes iguales por barras verticales.$ $Un rectángulo dividido en cinco partes iguales por barras verticales. Las tres barras más a la izquierda están sombreadas.$
2a: Un rectángulo entero 2b: Todo el rectángulo dividido en 5 partes iguales 2c: 3 de las 5 partes iguales

Figura 2.

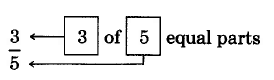
$La fracción tres quintas partes. Esto se leería, 3 de 5 partes iguales.$

La fracción$\dfrac{3}{5}$ “se lee como “tres quintos”.

Conjunto de Muestras A

$Una línea numérica con dos marcas, 0 y 1.$
3a: La línea numérica entre 0 y 1

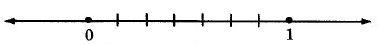
$Una línea numérica con dos marcas, 0 y 1, y seis marcas hash en el medio.$
3b: La línea numérica entre 0 y 1 dividida en 7 partes iguales

$Una línea numérica con dos marcas, 0 y 1, y seis marcas hash en el medio. Hay una flecha dibujada desde el cero hasta la primera marca hash, y luego de esa marca hash a la siguiente, hasta la sexta marca hash, donde las flechas se detienen.$
3c: 6 de las 7 partes iguales

Figura 3.

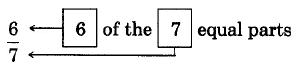
$La fracción seis-séptimas. Esto se leería, 6 de las 7 partes iguales.$

La fracción$\dfrac{6}{7}$ se lee como “seis séptimos”.

Conjunto de Muestras A

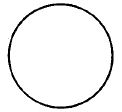
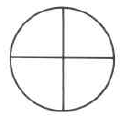
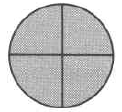
$Todo un círculo.$ $Un círculo entero dividido en cuatro partes iguales.$ $Un círculo entero dividido en cuatro partes iguales. Las cuatro partes están sombreadas.$
4a: Un círculo entero 4b: Todo el círculo dividido en 4 partes iguales 4c: 4 de las 4 partes iguales

Figura 4.

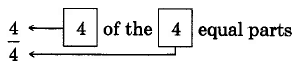
$La fracción cuatro cuartas partes. Esto se leería, 4 de las 4 partes iguales.$

Cuando el numerador y el denominador son iguales, la fracción representa la cantidad total, y su valor es 1.

$\dfrac{\text{nonzero whole number}}{\text{same nonzero whole number}} = 1$

Conjunto de práctica A

Especifique el numerador y denominador de las siguientes fracciones.

$\dfrac{4}{7}$

Contestar: 4, 7

Conjunto de práctica A

$\dfrac{5}{8}$

Contestar: 5, 8

Conjunto de práctica A

$\dfrac{10}{15}$

Contestar: 10, 15

Conjunto de práctica A

$\dfrac{1}{9}$

Contestar: 1, 9

Conjunto de práctica A

$\dfrac{0}{2}$

Contestar: 0, 2

Lectura y Escritura de Fracciones

Para traducir correctamente las fracciones de forma de palabra a forma numérica, o de forma numérica a forma de palabra, es necesario entender el uso del guión.

Uso del guión
Uno de los usos principales del guión es decirle al lector que dos palabras que no se unen ordinariamente deben tomarse en combinación como una unidad. Los guiones siempre se utilizan para números entre 21 y 99 (excepto los que terminan en cero).

Conjunto de Muestras B

Escribe cada fracción usando números enteros.

Cincuenta y trescentésimas. El guión une las palabras tres y centésimas y nos dice que las consideremos como una sola unidad. Por lo tanto, cincuenta y tres centésimas se traduce como$\dfrac{50}{300}$

Conjunto de Muestras B

Cincuenta y tres centésimas. El guión une los números cincuenta y tres y nos dice que los consideremos como una sola unidad. Por lo tanto, cincuenta y tres centésimas se traduce como$\dfrac{53}{100}$

Conjunto de Muestras B

Cuatrocientos siete milésimas. El guión une las palabras siete y milésimas y nos dice que las consideremos como una sola unidad. Por lo tanto, cuatrocientos siete milésimas se traduce como$\dfrac{400}{7,000}$

Conjunto de Muestras B

Cuatrocientos siete milésimas. La ausencia de guiones indica que las palabras siete y milésimas deben considerarse individualmente. cuatrocientos siete milésimas se traduce como$\dfrac{407}{1000}$

Escribe cada fracción usando palabras.

Conjunto de Muestras B

$\dfrac{21}{85}$se traduce como veintiún ochenta y cinco.

Conjunto de Muestras B

$\dfrac{200}{3,000}$se traduce como doscientos tres milésimas. Se necesita un guión entre las palabras tres y milésimas para decirle al lector que estas palabras deben considerarse como una sola unidad.

Conjunto de Muestras B

$\dfrac{203}{1,000}$se traduce como doscientos tres milésimas.

Set de práctica B

Escribe las siguientes fracciones usando números enteros.

una décima

Contestar: $\dfrac{1}{10}$

Set de práctica B

once decimocuarto

Contestar: $\dfrac{11}{14}$

Set de práctica B

dieciséis treinta y quintos

Contestar: $\dfrac{16}{35}$

Set de práctica B

ochocientos siete milésimas

Contestar: $\dfrac{800}{7,000}$

Escribe lo siguiente usando palabras.

Set de práctica B

$\dfrac{3}{8}$

Contestar: tres octavos

Set de práctica B

$\dfrac{1}{10}$

Contestar: una décima

Set de práctica B

$\dfrac{3}{250}$

Contestar: tres doscientos cincuenta

Set de práctica B

$\dfrac{114}{3,190}$

Contestar: ciento catorce tres mil ciento noventa

Nombra la fracción que describe cada porción sombreada.

Set de práctica B

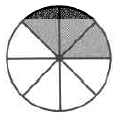
$Un círculo entero dividido en ocho partes iguales, con tres partes sombreadas.$

Contestar: $\dfrac{3}{8}$

Set de práctica B

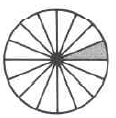
$Un círculo entero dividido en dieciséis partes iguales, con una parte sombreada.$

Contestar: $\dfrac{1}{16}$

En los siguientes 2 problemas, indique el numerador y denominador, y escriba cada fracción en palabras.

Set de práctica B

El número$\dfrac{5}{9}$ se utiliza para convertir de Fahrenheit a Celsius.

Contestar: 5, 9, cinco novenos

Set de práctica B

Un centavo es$\dfrac{1}{10}$ de un dólar.

Contestar: 1, 10, una décima

Ejercicios

Para los siguientes 10 problemas, especifique el numerador y denominador en cada fracción.

Ejercicio$\PageIndex{1}$

$\dfrac{3}{4}$

Contestar: numerador, 3; denominador, 4

Ejercicio$\PageIndex{2}$

$\dfrac{9}{10}$

Ejercicio$\PageIndex{3}$

$\dfrac{1}{5}$

Contestar: numerador, 1; denominador, 5

Ejercicio$\PageIndex{4}$

$\dfrac{5}{6}$

Ejercicio$\PageIndex{5}$

$\dfrac{7}{7}$

Contestar: numerador, 7; denominador, 7

Ejercicio$\PageIndex{6}$

$\dfrac{4}{6}$

Ejercicio$\PageIndex{7}$

$\dfrac{0}{12}$

Contestar: numerador, 0; denominador, 12

Ejercicio$\PageIndex{8}$

$\dfrac{25}{25}$

Ejercicio$\PageIndex{9}$

$\dfrac{18}{1}$

Contestar: numerador, 18; denominador, 1

Ejercicio$\PageIndex{10}$

$\dfrac{0}{16}$

Para los siguientes 10 problemas, escriba las fracciones usando números enteros.

Ejercicio$\PageIndex{11}$

cuatro quintas

Contestar: $\dfrac{4}{5}$

Ejercicio$\PageIndex{12}$

dos novenos

Ejercicio$\PageIndex{13}$

quince veinteavos

Contestar: $\dfrac{15}{20}$

Ejercicio$\PageIndex{14}$

cuarenta y siete ochenta y tercios

Ejercicio$\PageIndex{15}$

noventa y uno ciento séptumos

Contestar: $\dfrac{91}{107}$

Ejercicio$\PageIndex{16}$

veintidós cuatrocientos once

Ejercicio$\PageIndex{17}$

seiscientos quinientos ochocientos treinta y cuartos

Contestar: $\dfrac{605}{834}$

Ejercicio$\PageIndex{18}$

tres mil tres cuarenta y cuatro diez milésimas

Ejercicio$\PageIndex{19}$

noventa y dos millonésimas

Contestar: $\dfrac{92}{1,000,000}$

Ejercicio$\PageIndex{20}$

uno tres mil millonésimas

Para los siguientes 10 problemas, escribe las fracciones usando palabras.

Ejercicio$\PageIndex{21}$

$\dfrac{5}{9}$

Contestar: cinco novenos

Ejercicio$\PageIndex{22}$

$\dfrac{6}{10}$

Ejercicio$\PageIndex{23}$

$\dfrac{8}{15}$

Contestar: ocho quintas

Ejercicio$\PageIndex{24}$

$\dfrac{10}{13}$

Ejercicio$\PageIndex{25}$

$\dfrac{75}{100}$

Contestar: setenta y cinco centésimas

Ejercicio$\PageIndex{26}$

$\dfrac{86}{135}$

Ejercicio$\PageIndex{27}$

$\dfrac{916}{1,014}$

Contestar: novecientos dieciséis mil catorce

Ejercicio$\PageIndex{28}$

$\dfrac{501}{10,001}$

Ejercicio$\PageIndex{29}$

$\dfrac{18}{31,608}$

Contestar: dieciocho treinta y uno mil seiscientos octavos

Ejercicio$\PageIndex{30}$

$\dfrac{1}{500,000}$

Para los siguientes 4 problemas, nombra la fracción correspondiente a la porción sombreada.

Ejercicio$\PageIndex{31}$

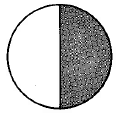
$Un círculo entero dividido en dos partes iguales, con una parte sombreada.$

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{32}$

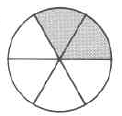
$Un círculo entero dividido en seis partes iguales, con dos partes sombreadas.$

Ejercicio$\PageIndex{33}$

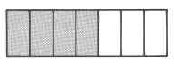
$Un rectángulo dividido en siete partes iguales, con cuatro partes sombreadas.$

Contestar: $\dfrac{4}{7}$

Ejercicio$\PageIndex{34}$

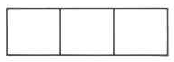
$Un rectángulo dividido en tres partes iguales, con cero partes sombreadas.$

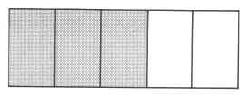
Para los siguientes 4 problemas, sombree la porción correspondiente a la fracción dada en la figura dada.

Ejercicio$\PageIndex{35}$

$\dfrac{3}{5}$

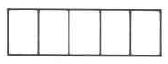
$Un rectángulo dividido en cinco partes iguales.$

Contestar: $Un rectángulo dividido en cinco partes iguales, con tres partes sombreadas.$

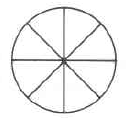
Ejercicio$\PageIndex{36}$

$\dfrac{1}{8}$

$Un círculo dividido en ocho partes iguales.$

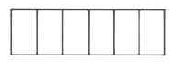
Ejercicio$\PageIndex{37}$

$\dfrac{6}{6}$

$Un rectángulo dividido en seis partes iguales.$

Contestar: $Un rectángulo dividido en seis partes iguales, con las seis partes sombreadas.$

Ejercicio$\PageIndex{38}$

$\dfrac{0}{3}$

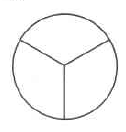
$Un círculo dividido en tres partes iguales.$

Indicar el numerador y denominador y escribir con palabras cada una de las fracciones que aparecen en los enunciados para los siguientes 10 problemas.

Ejercicio$\PageIndex{39}$

Un contratista está vendiendo casas en lotes de$\dfrac{1}{4}$ acres.

Contestar: Numerador, 1; denominador, 4; un cuarto

Ejercicio$\PageIndex{40}$

La fracción$\dfrac{22}{7}$ se utiliza a veces como una aproximación al número$\pi$. (El símbolo se lee “pi.”)

Ejercicio$\PageIndex{41}$

La fracción$\dfrac{4}{3}$ se utiliza para encontrar el volumen de una esfera.

Contestar: Numerador, 4; denominador, 3; cuatro tercios

Ejercicio$\PageIndex{42}$

Una pulgada es$\dfrac{1}{12}$ de pie.

Ejercicio$\PageIndex{43}$

Acerca$\dfrac{2}{7}$ de los alumnos de una clase universitaria de estadística recibieron una “B” en el curso.

Contestar: Numerador, 2; denominador, 7; dos séptimos

Ejercicio$\PageIndex{44}$

La probabilidad de seleccionar aleatoriamente un palo al sacar una carta de una baraja estándar de 52 cartas es$\dfrac{13}{52}$.

Ejercicio$\PageIndex{45}$

En una caja que contiene ocho chips de computadora, se sabe que cinco son buenos y tres son defectuosos. Si se seleccionan tres chips al azar, la probabilidad de que los tres sean defectuosos es$\dfrac{1}{56}$.

Contestar: Numerador, 1; denominador, 56; un quincuagésimo sexto

Ejercicio$\PageIndex{46}$

En una habitación de 25 personas, la probabilidad de que al menos dos personas tengan la misma fecha de nacimiento (fecha y mes, no año) es$\dfrac{569}{1000}$.

Ejercicio$\PageIndex{47}$

La media (promedio) de los números 21, 25, 43 y 36 es$\dfrac{125}{4}$.

Contestar: Numerador, 125; denominador, 4; ciento veinticinco cuartas partes

Ejercicio$\PageIndex{48}$

Si una roca cae desde una altura de 20 metros sobre Júpiter, la roca tendrá$\dfrac{32}{25}$ metros de altura después de$\dfrac{6}{5}$ segundos.

Ejercicios para revisión

Ejercicio$\PageIndex{49}$

Utilice los números 3 y 11 para ilustrar la propiedad conmutativa de la suma.

Contestar: $3 + 11 = 11 + 3 = 14$

Ejercicio$\PageIndex{50}$

Encuentra el cociente. $676 \div 26$

Ejercicio$\PageIndex{51}$

Escribir$7 \cdot 7 \cdot 7 \cdot 7 \cdot 7$ usando exponentes.

Contestar: $7^5$

Ejercicio$\PageIndex{52}$

Encuentra el valor de$\dfrac{8 \cdot (6 + 20)}{8} + \dfrac{3 \cdot (6 + 16)}{22}$.

Ejercicio$\PageIndex{53}$

Encuentra el múltiplo menos común de 12, 16 y 18.

Contestar: 144