4.9: Examen de Aptitud

Última actualización
Guardar como PDF

Page ID: 116705

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicio$\PageIndex{1}$

Sombra una porción que corresponda a la fracción$\dfrac{5}{8}$

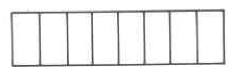
$Un rectángulo dividido en ocho partes.$

Contestar: $Un rectángulo dividido en ocho partes. Cinco partes están sombreadas.$

Ejercicio$\PageIndex{2}$

Especificar el numerador y denominador de la fracción$\dfrac{5}{9}$.

Contestar: Numerador, 5; denominador, 9

Ejercicio$\PageIndex{3}$

Escribe la fracción cinco once.

Contestar: $\dfrac{5}{11}$

Ejercicio$\PageIndex{4}$

Escribe, en palabras,$\dfrac{4}{5}$

Contestar: Cuatro quintas partes

Ejercicio$\PageIndex{5}$

¿Cuál de las fracciones es una fracción propiamente dicha? $4 \dfrac{1}{12}$,$\dfrac{5}{12}$,$\dfrac{12}{5}$

Contestar: $\dfrac{5}{12}$

Ejercicio$\PageIndex{6}$

Convertir$3 \dfrac{4}{7}$ a una fracción impropia.

Contestar: $\dfrac{25}{7}$

Ejercicio$\PageIndex{7}$

Convertir$\dfrac{16}{5}$ a un número mixto.

Contestar: $3 \dfrac{1}{5}$

Ejercicio$\PageIndex{8}$

Determinar si$\dfrac{5}{12}$ y$\dfrac{20}{48}$ son fracciones equivalentes.

Contestar: si

Para problemas 9-11, reducir, si es posible, cada fracción a los términos más bajos.

Ejercicio$\PageIndex{9}$

$\dfrac{21}{35}$

Contestar: $\dfrac{3}{5}$

Ejercicio$\PageIndex{10}$

$\dfrac{15}{51}$

Contestar: $\dfrac{5}{17}$

Ejercicio$\PageIndex{11}$

$\dfrac{104}{480}$

Contestar: $\dfrac{13}{60}$

Para los problemas 12 y 13, determine el numerador o denominador faltante.

Ejercicio$\PageIndex{12}$

$\dfrac{5}{9} = \dfrac{?}{36}$

Contestar: 20

Ejercicio$\PageIndex{13}$

$\dfrac{4}{3} = \dfrac{32}{?}$

Contestar: 24

Para problemas 14-25, encuentra cada valor.

Ejercicio$\PageIndex{14}$

$\dfrac{15}{16} \cdot \dfrac{4}{25}$

Contestar: $\dfrac{3}{20}$

Ejercicio$\PageIndex{15}$

$3 \dfrac{3}{4} \cdot 2 \dfrac{2}{9} \cdot 6 \dfrac{3}{5}$

Contestar: 55

Ejercicio$\PageIndex{16}$

$\sqrt{\dfrac{25}{36}}$

Contestar: $\dfrac{5}{6}$

Ejercicio$\PageIndex{17}$

$\sqrt{\dfrac{4}{9}} \cdot \sqrt{\dfrac{81}{64}}$

Contestar: $\dfrac{3}{4}$

Ejercicio$\PageIndex{18}$

$\dfrac{11}{30} \cdot \sqrt{\dfrac{225}{121}}$

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{19}$

$\dfrac{4}{15} \div 8$

Contestar: $\dfrac{1}{30}$

Ejercicio$\PageIndex{20}$

$\dfrac{8}{15} \cdot \dfrac{5}{12} \div 2 \dfrac{4}{9}$

Contestar: $\dfrac{1}{11}$

Ejercicio$\PageIndex{21}$

$(\dfrac{6}{5})^3 \div \sqrt{1 \dfrac{11}{15}}$

Contestar: $\dfrac{36}{25} = 1 \dfrac{11}{25}$

Ejercicio$\PageIndex{22}$

Hallar$\dfrac{5}{12}$ de$\dfrac{24}{25}$.

Contestar: $\dfrac{2}{5}$

Ejercicio$\PageIndex{23}$

$\dfrac{2}{9}$¿de qué número es$\dfrac{1}{18}$?

Contestar: $\dfrac{1}{4}$

Ejercicio$\PageIndex{24}$

$1\dfrac{5}{7}$de$\dfrac{21}{20}$ es ¿qué número?

Contestar: $\dfrac{9}{5} = 1 \dfrac{4}{5}$

Ejercicio$\PageIndex{25}$

¿Qué parte de$\dfrac{9}{14}$ es$\dfrac{6}{7}$?

Contestar: $\dfrac{4}{3}$o$1 \dfrac{1}{3}$