4.8: Suplemento de ejercicio

Última actualización
Guardar como PDF

Page ID: 116719

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Fracciones de números enteros

Para Problemas 1 y 2, nombra la fracción sugerida.

Ejercicio$\PageIndex{1}$

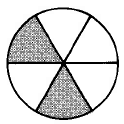
$Un círculo dividido en seis partes iguales. Dos partes están sombreadas.$

Contestar: $\dfrac{2}{6}$o$\dfrac{1}{3}$

Ejercicio$\PageIndex{2}$

$Un rectángulo dividido en ocho partes. Cuatro partes están sombreadas.$

Para los problemas 3-5, especifique el numerador y el denominador.

Ejercicio$\PageIndex{3}$

$\dfrac{4}{5}$

Contestar: numerador, 4; denominador, 5

Ejercicio$\PageIndex{4}$

$\dfrac{5}{12}$

Ejercicio$\PageIndex{5}$

$\dfrac{1}{3}$

Contestar: numerador, 1; denominador, 3

Para problemas 6-10, escriba cada fracción usando dígitos.

Ejercicio$\PageIndex{6}$

Tres quintas partes

Ejercicio$\PageIndex{7}$

Ocho once

Contestar: $\dfrac{8}{11}$

Ejercicio$\PageIndex{8}$

Sesenta y uno cuarenta primeros

Ejercicio$\PageIndex{9}$

Doscientos seis milésimas

Contestar: $\dfrac{200}{6,000}$

Ejercicio$\PageIndex{10}$

cero décimas

Para los problemas 11-15, escribe cada fracción usando palabras.

Ejercicio$\PageIndex{11}$

$\dfrac{10}{17}$

Contestar: diez diecisiete

Ejercicio$\PageIndex{12}$

$\dfrac{21}{38}$

Ejercicio$\PageIndex{13}$

$\dfrac{606}{1431}$

Contestar: seiscientos seis, mil cuatrocientos treinta y primeros

Ejercicio$\PageIndex{14}$

$\dfrac{0}{8}$

Ejercicio$\PageIndex{15}$

$\dfrac{1}{16}$

Contestar: decimosexto

Para los problemas 16-18, indica cada numerador y denominador y escribe cada fracción usando dígitos.

Ejercicio$\PageIndex{16}$

Un minuto es sesenta de hora.

Ejercicio$\PageIndex{17}$

En una caja que contiene cuarenta y cinco componentes electrónicos, se sabe que ocho son defectuosos. Si se eligen tres componentes al azar de la caja, la probabilidad de que los tres sean defectuosos es de cincuenta y seis catorce mil ciento noventa.

Contestar: numerador, 56; denominador, 14,190

Ejercicio$\PageIndex{18}$

Alrededor de tres quintas partes de los alumnos de una clase de álgebra universitaria recibieron una “B” en el curso.

Para los problemas 19 y 20, sombrear la región correspondiente a la fracción dada.

Ejercicio$\PageIndex{19}$

$\dfrac{1}{4}$

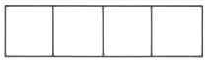
$Un rectángulo dividido en cuatro partes.$

Contestar: $Un rectángulo dividido en cuatro partes. Una parte está sombreada.$

Ejercicio$\PageIndex{20}$

$\dfrac{3}{7}$

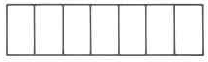
$Un rectángulo dividido en siete partes.$

Fracción apropiada, fracción impropia y números mixtos

Para problemas 21-29, convierta cada fracción impropia a un número mixto.

Ejercicio$\PageIndex{21}$

$\dfrac{11}{4}$

Contestar: $2 \dfrac{3}{4}$

Ejercicio$\PageIndex{22}$

$\dfrac{15}{2}$

Ejercicio$\PageIndex{23}$

$\dfrac{51}{8}$

Contestar: $6 \dfrac{3}{8}$

Ejercicio$\PageIndex{24}$

$\dfrac{121}{15}$

Ejercicio$\PageIndex{25}$

$\dfrac{356}{3}$

Contestar: $118 \dfrac{2}{3}$

Ejercicio$\PageIndex{26}$

$\dfrac{3}{2}$

Ejercicio$\PageIndex{27}$

$\dfrac{5}{4}$

Contestar: $1 \dfrac{1}{4}$

Ejercicio$\PageIndex{28}$

$\dfrac{20}{5}$

Ejercicio$\PageIndex{29}$

$\dfrac{9}{3}$

Contestar: 3

Para problemas 30-40, convierta cada número mixto a una fracción impropia.

Ejercicio$\PageIndex{30}$

$5 \dfrac{2}{3}$

Ejercicio$\PageIndex{31}$

$16 \dfrac{1}{8}$

Contestar: $\dfrac{129}{8}$

Ejercicio$\PageIndex{32}$

$18 \dfrac{1}{3}$

Ejercicio$\PageIndex{33}$

$3 \dfrac{1}{5}$

Contestar: $\dfrac{16}{5}$

Ejercicio$\PageIndex{34}$

$2 \dfrac{9}{16}$

Ejercicio$\PageIndex{35}$

$17 \dfrac{20}{21}$

Contestar: $\dfrac{377}{21}$

Ejercicio$\PageIndex{36}$

$1 \dfrac{7}{8}$

Ejercicio$\PageIndex{37}$

$1 \dfrac{1}{2}$

Contestar: $\dfrac{3}{2}$

Ejercicio$\PageIndex{38}$

$2 \dfrac{1}{2}$

Ejercicio$\PageIndex{39}$

$8 \dfrac{6}{7}$

Contestar: $\dfrac{62}{7}$

Ejercicio$\PageIndex{40}$

$2 \dfrac{9}{2}$

Ejercicio$\PageIndex{41}$

¿Por qué$0 \dfrac{1}{12}$ no califica como número mixto?

Contestar: porque la parte del número entero es cero

Ejercicio$\PageIndex{42}$

¿Por qué 8 califica como número mixto?

Fracciones equivalentes, reducción de fracciones a términos más bajos y aumento de fracciones a término superior

Para los problemas 43-47, determinar si los pares de fracciones son equivalentes.

Ejercicio$\PageIndex{43}$

$\dfrac{1}{2}, \dfrac{15}{30}$

Contestar: equivalente

Ejercicio$\PageIndex{44}$

$\dfrac{8}{9}, \dfrac{32}{36}$

Ejercicio$\PageIndex{45}$

$\dfrac{3}{14}, \dfrac{24}{110}$

Contestar: no equivalente

Ejercicio$\PageIndex{46}$

$2 \dfrac{3}{8}, \dfrac{38}{16}$

Ejercicio$\PageIndex{47}$

$\dfrac{108}{77}, 1 \dfrac{5}{13}$

Contestar: no equivalente

Para problemas 48-60, reducir, si es posible, cada fracción.

Ejercicio$\PageIndex{48}$

$\dfrac{10}{25}$

Ejercicio$\PageIndex{49}$

$\dfrac{32}{44}$

Contestar: $\dfrac{8}{11}$

Ejercicio$\PageIndex{50}$

$\dfrac{102}{266}$

Ejercicio$\PageIndex{51}$

$\dfrac{15}{33}$

Contestar: $\dfrac{5}{11}$

Ejercicio$\PageIndex{52}$

$\dfrac{18}{25}$

Ejercicio$\PageIndex{53}$

$\dfrac{21}{35}$

Contestar: $\dfrac{3}{5}$

Ejercicio$\PageIndex{54}$

$\dfrac{9}{16}$

Ejercicio$\PageIndex{55}$

$\dfrac{45}{85}$

Contestar: $\dfrac{9}{17}$

Ejercicio$\PageIndex{56}$

$\dfrac{24}{42}$

Ejercicio$\PageIndex{57}$

$\dfrac{70}{136}$

Contestar: $\dfrac{35}{68}$

Ejercicio$\PageIndex{58}$

$\dfrac{182}{580}$

Ejercicio$\PageIndex{59}$

$\dfrac{325}{810}$

Contestar: $\dfrac{65}{162}$

Ejercicio$\PageIndex{60}$

$\dfrac{250}{1000}$

Para problemas 61-72, determinar el numerador o denominador faltante.

Ejercicio$\PageIndex{61}$

$\dfrac{3}{7} = \dfrac{?}{35}$

Contestar: 15

Ejercicio$\PageIndex{62}$

$\dfrac{4}{11} = \dfrac{?}{99}$

Ejercicio$\PageIndex{63}$

$\dfrac{1}{12} = \dfrac{?}{72}$

Contestar: 6

Ejercicio$\PageIndex{64}$

$\dfrac{5}{8} = \dfrac{25}{?}$

Ejercicio$\PageIndex{65}$

$\dfrac{11}{9} = \dfrac{33}{?}$

Contestar: 27

Ejercicio$\PageIndex{66}$

$\dfrac{4}{15} = \dfrac{24}{?}$

Ejercicio$\PageIndex{67}$

$\dfrac{14}{15} = \dfrac{?}{45}$

Contestar: 42

Ejercicio$\PageIndex{68}$

$\dfrac{0}{5} = \dfrac{?}{20}$

Ejercicio$\PageIndex{69}$

$\dfrac{12}{21} = \dfrac{96}{?}$

Contestar: 168

Ejercicio$\PageIndex{70}$

$\dfrac{14}{23} = \dfrac{?}{253}$

Ejercicio$\PageIndex{71}$

$\dfrac{15}{16} = \dfrac{180}{?}$

Contestar: 192

Ejercicio$\PageIndex{72}$

$\dfrac{21}{22} = \dfrac{336}{?}$

Multiplicación y división de fracciones ([link], [link])

Para problemas 73-95, realizar cada multiplicación y división.

Ejercicio$\PageIndex{73}$

$\dfrac{4}{5} \cdot \dfrac{15}{16}$

Contestar: $\dfrac{3}{4}$

Ejercicio$\PageIndex{74}$

$\dfrac{8}{9} \cdot \dfrac{3}{24}$

Ejercicio$\PageIndex{75}$

$\dfrac{1}{10} \cdot \dfrac{5}{12}$

Contestar: $\dfrac{1}{24}$

Ejercicio$\PageIndex{76}$

$\dfrac{14}{15} \cdot \dfrac{7}{5}$

Ejercicio$\PageIndex{77}$

$\dfrac{5}{6} \cdot \dfrac{13}{22} \cdot \dfrac{11}{39}$

Contestar: $\dfrac{5}{36}$

Ejercicio$\PageIndex{78}$

$\dfrac{2}{3} \div \dfrac{15}{7} \cdot \dfrac{5}{6}$

Ejercicio$\PageIndex{79}$

$3 \dfrac{1}{2} \div \dfrac{7}{2}$

Contestar: 1

Ejercicio$\PageIndex{80}$

$2 \dfrac{4}{9} \div \dfrac{11}{45}$

Ejercicio$\PageIndex{81}$

$\dfrac{8}{15} \cdot \dfrac{3}{16} \cdot \dfrac{5}{24}$

Contestar: $\dfrac{1}{48}$

Ejercicio$\PageIndex{82}$

$\dfrac{8}{15} \div 3 \dfrac{3}{5} \cdot \dfrac{9}{16}$

Ejercicio$\PageIndex{83}$

$\dfrac{14}{15} \div 3 \dfrac{8}{9} \cdot \dfrac{10}{21}$

Contestar: $\dfrac{4}{35}$

Ejercicio$\PageIndex{84}$

$18 \cdot 5 \dfrac{3}{4}$

Ejercicio$\PageIndex{85}$

$3 \dfrac{3}{7} \cdot 2 \dfrac{1}{12}$

Contestar: $\dfrac{50}{7} = 7 \dfrac{1}{7}$

Ejercicio$\PageIndex{86}$

$4 \dfrac{1}{2} \div 2 \dfrac{4}{7}$

Ejercicio$\PageIndex{87}$

$6 \dfrac{1}{2} \div 3 \dfrac{1}{4}$

Contestar: 2

Ejercicio$\PageIndex{88}$

$3 \dfrac{5}{16} \div 2 \dfrac{7}{18}$

Ejercicio$\PageIndex{89}$

$7 \div 2 \dfrac{1}{3}$

Contestar: 3

Ejercicio$\PageIndex{90}$

$17 \div 4 \dfrac{1}{4}$

Ejercicio$\PageIndex{91}$

$\dfrac{5}{8} \div 1 \dfrac{1}{4}$

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{92}$

$2 \dfrac{2}{3} \cdot 3 \dfrac{3}{4}$

Ejercicio$\PageIndex{93}$

$20 \cdot \dfrac{18}{4}$

Contestar: 90

Ejercicio$\PageIndex{94}$

$0 \div 4 \dfrac{1}{8}$

Ejercicio$\PageIndex{95}$

$1 \div 6 \dfrac{1}{4} \cdot \dfrac{25}{4}$

Contestar: 1

Aplicaciones que involucran fracciones

Ejercicio$\PageIndex{96}$

Encuentra$\dfrac{8}{9}$ de$\dfrac{27}{2}$

Ejercicio$\PageIndex{97}$

¿Qué parte de$\dfrac{3}{8}$ es$\dfrac{21}{16}$?

Contestar: $\dfrac{7}{2}$o$3 \dfrac{1}{2}$

Ejercicio$\PageIndex{98}$

¿Qué parte de$3 \dfrac{1}{5}$ es$1 \dfrac{7}{25}$?

Ejercicio$\PageIndex{99}$

Hallar$6 \dfrac{2}{3}$ de$\dfrac{9}{15}$.

Contestar: 4

Ejercicio$\PageIndex{100}$

$\dfrac{7}{20}$de que numero es$\dfrac{14}{35}$?

Ejercicio$\PageIndex{101}$

¿Qué parte de$4 \dfrac{1}{16}$ es$3 \dfrac{3}{4}$?

Contestar: $\dfrac{12}{13}$

Ejercicio$\PageIndex{102}$

Encuentra$8 \dfrac{3}{10}$ de$16 \dfrac{2}{3}$

Ejercicio$\PageIndex{103}$

$\dfrac{3}{20}$de que numero es$\dfrac{18}{30}$?

Contestar: 4

Ejercicio$\PageIndex{104}$

Hallar$\dfrac{1}{3}$ de 0.

Ejercicio$\PageIndex{105}$

Hallar$\dfrac{11}{12}$ de 1.

Contestar: $\dfrac{11}{12}$