4.11: Suma y resta números mixtos (Parte 2)
- Page ID
- 114261
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Restar números mixtos con un denominador común
Ahora restaremos números mixtos sin usar un modelo. Pero puede ser útil que te imagines el modelo en tu mente mientras lees los pasos.
Paso 1. Reescribir el problema en forma vertical.
Paso 2. Compara las dos fracciones.
- Si la fracción superior es mayor que la fracción inferior, vaya al Paso 3.
- Si no, en el número mixto superior, tomar un todo y agregarlo a la parte de fracción, haciendo un número mixto con una fracción impropia.
Paso 3. Resta las fracciones.
Paso 4. Resta los números enteros.
Paso 5. Simplificar, si es posible.
Encuentra la diferencia:\(5 \dfrac{3}{5} − 2 \dfrac{4}{5}\).
Solución
| Reescribir el problema en forma vertical. | \(\begin{split} & 5 \dfrac{3}{5} \\ - & 2 \dfrac{4}{5} \\ \hline \end{split}\) |
| Ya que\(\dfrac{3}{5}\) es menor que\(\dfrac{4}{5}\), toma 1 del 5 y agrégalo a la\(\dfrac{3}{5}\):\(\left(\dfrac{5}{5} + \dfrac{3}{5} = \dfrac{8}{5}\right)\) | 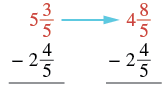 |
| Resta las fracciones. | \(\begin{split} & 4 \textcolor{red}{\dfrac{8}{5}} \\ - & 2 \textcolor{red}{\dfrac{4}{5}} \\ \hline \\ & \; \textcolor{red}{\dfrac{4}{5}} \end{split}\) |
| Resta las partes enteras. El resultado es en la forma más simple. | \(\begin{split} & \textcolor{red}{4} \dfrac{8}{5} \\ - & \textcolor{red}{2} \dfrac{4}{5} \\ \hline \\ & 2 \dfrac{4}{5} \end{split}\) |
Ya que el problema se dio con números mixtos, dejamos el resultado como números mixtos.
Encuentra la diferencia:\(6 \dfrac{4}{9} − 3 \dfrac{7}{9}\).
- Contestar
-
\(2\dfrac{2}{3}\)
Encuentra la diferencia:\(4 \dfrac{4}{7} − 2 \dfrac{6}{7}\).
- Contestar
-
\(1\dfrac{5}{7}\)
Así como lo hicimos con la suma, podríamos restar números mixtos convirtiéndolos primero en fracciones impropias. Deberíamos escribir la respuesta en la forma en que se dio, así que si nos dan números mixtos para restar escribiremos la respuesta como un número mixto.
Paso 1. Reescribe los números mixtos como fracciones impropias.
Paso 2. Resta los numeradores.
Paso 3. Escribe la respuesta como un número mixto, simplificando la parte de fracción, si es posible.
Encuentra la diferencia convirtiendo a fracciones impropias:\(9 \dfrac{6}{11} − 7 \dfrac{10}{11}\).
Solución
| Reescribir como fracciones impropias. | \(\dfrac{105}{11} - \dfrac{87}{11}\) |
| Resta los numeradores. | \(\dfrac{18}{11}\) |
| Reescribir como un número mixto. | \(1 \dfrac{7}{11}\) |
Encuentra la diferencia convirtiendo a fracciones impropias:\(6 \dfrac{4}{9} − 3 \dfrac{7}{9}\).
- Contestar
-
\(2\dfrac{2}{3}\)
Encuentra la diferencia convirtiendo a fracciones impropias:\(4 \dfrac{4}{7} − 2 \dfrac{6}{7}\).
- Contestar
-
\(1\dfrac{5}{7}\)
Sumar y restar números mixtos con diferentes denominadores
Para sumar o restar números mixtos con diferentes denominadores, primero convertimos las fracciones a fracciones equivalentes con la LCD. Entonces podemos seguir todos los pasos que usamos anteriormente para sumar o restar fracciones con denominadores similares.
Agregar:\(2 \dfrac{1}{2} + 5 \dfrac{2}{3}\).
Solución
Dado que los denominadores son diferentes, reescribimos las fracciones como fracciones equivalentes con la LCD,\(6\). Entonces agregaremos y simplificaremos.
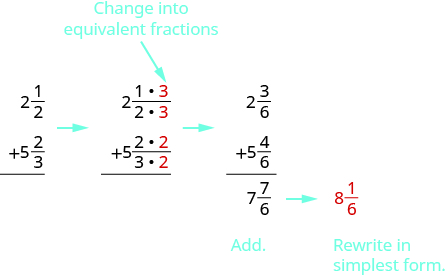
Escribimos la respuesta como un número mixto porque nos dieron números mixtos en el problema.
Agregar:\(1 \dfrac{5}{6} + 4 \dfrac{3}{4}\).
- Contestar
-
\(6\dfrac{7}{12}\)
Agregar:\(3 \dfrac{4}{5} + 8 \dfrac{1}{2}\).
- Contestar
-
\(12\dfrac{3}{10}\)
Resta:\(4 \dfrac{3}{4} − 2 \dfrac{7}{8}\).
Solución
Dado que los denominadores de las fracciones son diferentes, los reescribiremos como fracciones equivalentes con la LCD\(8\). Una vez en esa forma, restaremos. Pero\(1\) primero tendremos que pedir prestado.
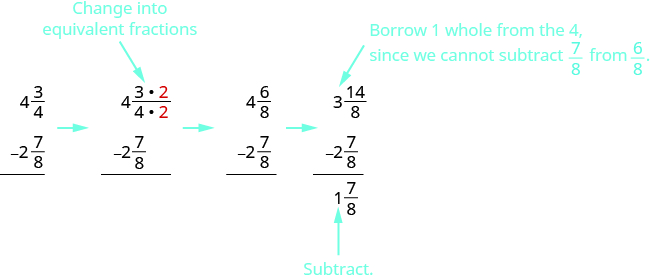
Nos dieron números mixtos, así que dejamos la respuesta como un número mixto.
Encuentra la diferencia:\(8 \dfrac{1}{2} − 3 \dfrac{4}{5}\).
- Contestar
-
\(4\dfrac{7}{10}\)
Encuentra la diferencia:\(4 \dfrac{3}{4} − 1 \dfrac{5}{6}\).
- Contestar
-
\(2\dfrac{11}{12}\)
Resta:\(3 \dfrac{5}{11} − 4 \dfrac{3}{4}\).
Solución
Podemos ver que la respuesta será negativa ya que estamos restando\(4\) de\(3\). Generalmente, cuando sabemos que la respuesta será negativa es más fácil restar con fracciones inadecuadas en lugar de números mixtos.
| Cambiar a fracciones equivalentes con la pantalla LCD. |
\(3 \dfrac{5 \cdot 4}{11 \cdot 4} - 4 \dfrac{3 \cdot 11}{4 \cdot 11}\) \(3 \dfrac{20}{44} - 4 \dfrac{33}{44}\) |
| Reescribir como fracciones impropias. | \(\dfrac{152}{44} - \dfrac{209}{44}\) |
| Restar. | \(- \dfrac{57}{44}\) |
| Reescribir como un número mixto. | \(- 1 \dfrac{13}{44}\) |
Resta:\(1 \dfrac{3}{4} − 6 \dfrac{7}{8}\).
- Contestar
-
\(-\dfrac{41}{8}\)
Resta:\(10 \dfrac{3}{7} − 22 \dfrac{4}{9}\).
- Contestar
-
\(-\dfrac{757}{63}\)
Acceda a recursos adicionales en línea
La práctica hace la perfección
Adición de modelos de números mixtos
En los siguientes ejercicios, utilice un modelo para encontrar la suma. Haz un dibujo para ilustrar tu modelo.
- \(1 \dfrac{1}{5} + 3 \dfrac{1}{5}\)
- \(2 \dfrac{1}{3} + 1 \dfrac{1}{3}\)
- \(1 \dfrac{3}{8} + 1 \dfrac{7}{8}\)
- \(1 \dfrac{5}{6} + 1 \dfrac{5}{6}\)
Agregar números mixtos con un denominador común
En los siguientes ejercicios, agregue.
- \(5 \dfrac{1}{3} + 6 \dfrac{1}{3}\)
- \(2 \dfrac{4}{9} + 5 \dfrac{1}{9}\)
- \(4 \dfrac{5}{8} + 9 \dfrac{3}{8}\)
- \(7 \dfrac{9}{10} + 3 \dfrac{1}{10}\)
- \(3 \dfrac{4}{5} + 6 \dfrac{4}{5}\)
- \(9 \dfrac{2}{3} + 1 \dfrac{2}{3}\)
- \(6 \dfrac{9}{10} + 8 \dfrac{3}{10}\)
- \(8 \dfrac{4}{9} + 2 \dfrac{8}{9}\)
Modelo de resta de números mixtos
En los siguientes ejercicios, usa un modelo para encontrar la diferencia. Haz un dibujo para ilustrar tu modelo.
- \(1 \dfrac{1}{6} - \dfrac{1}{6}\)
- \(1 \dfrac{1}{8} - \dfrac{1}{8}\)
Restar números mixtos con un denominador común
En los siguientes ejercicios, encuentra la diferencia.
- \(2 \dfrac{7}{8} - 1 \dfrac{3}{8}\)
- \(2 \dfrac{7}{12} - 1 \dfrac{5}{12}\)
- \(8 \dfrac{3}{7} - 4 \dfrac{4}{7}\)
- \(19 \dfrac{13}{15} - 13 \dfrac{7}{15}\)
- \(8 \dfrac{3}{7} - 4 \dfrac{4}{7}\)
- \(5 \dfrac{2}{9} - 3 \dfrac{4}{9}\)
- \(2 \dfrac{5}{8} - 1 \dfrac{7}{8}\)
- \(2 \dfrac{5}{12} - 1 \dfrac{7}{12}\)
Sumar y restar números mixtos con diferentes denominadores
En los siguientes ejercicios, escribe la suma o diferencia como un número mixto en forma simplificada.
- \(3 \dfrac{1}{4} + 6 \dfrac{1}{3}\)
- \(2 \dfrac{1}{6} + 5 \dfrac{3}{4}\)
- \(1 \dfrac{5}{8} + 4 \dfrac{1}{2}\)
- \(7 \dfrac{2}{3} + 8 \dfrac{1}{2}\)
- \(2 \dfrac{5}{12} - 1 \dfrac{7}{12}\)
- \(6 \dfrac{4}{5} - 1 \dfrac{1}{4}\)
- \(2 \dfrac{2}{3} - 3 \dfrac{1}{2}\)
- \(2 \dfrac{7}{8} - 4 \dfrac{1}{3}\)
Práctica Mixta
En los siguientes ejercicios, realice la operación indicada y escriba el resultado como un número mixto en forma simplificada.
- \(2 \dfrac{5}{8} \cdot 1 \dfrac{3}{4}\)
- \(1 \dfrac{2}{3} \cdot 4 \dfrac{1}{6}\)
- \(\dfrac{2}{7} + \dfrac{4}{7}\)
- \(\dfrac{2}{9} + \dfrac{5}{9}\)
- \(1 \dfrac{5}{12} \div \dfrac{1}{12}\)
- \(2 \dfrac{3}{10} \div \dfrac{1}{10}\)
- \(13 \dfrac{5}{12} - 9 \dfrac{7}{12}\)
- \(15 \dfrac{5}{8} - 6 \dfrac{7}{8}\)
- \(\dfrac{5}{9} - \dfrac{4}{9}\)
- \(\dfrac{11}{15} - \dfrac{7}{15}\)
- 4 −\(\dfrac{3}{4}\)
- 6 −\(\dfrac{2}{5}\)
- \(\dfrac{9}{20} \div \dfrac{3}{4}\)
- \(\dfrac{7}{24} \div \dfrac{14}{3}\)
- \(9 \dfrac{6}{11} + 7 \dfrac{10}{11}\)
- \(8 \dfrac{5}{13} + 4 \dfrac{9}{13}\)
- \(3 \dfrac{2}{5} + 5 \dfrac{3}{4}\)
- \(2 \dfrac{5}{6} + 4 \dfrac{1}{5}\)
- \(\dfrac{8}{15} \cdot \dfrac{10}{19}\)
- \(\dfrac{5}{12} \cdot \dfrac{8}{9}\)
- \(6 \dfrac{7}{8} - 2 \dfrac{1}{3}\)
- \(6 \dfrac{5}{9} - 4 \dfrac{2}{5}\)
- \(5 \dfrac{2}{9} - 4 \dfrac{4}{5}\)
- \(4 \dfrac{3}{8} - 3 \dfrac{2}{3}\)
Matemáticas cotidianas
- Coser Renata está cosiendo camisas a juego para su esposo e hijo. Según los patrones que usará, necesita\(2 \dfrac{3}{8}\) yardas de tela para la camisa de su esposo y\(1 \dfrac{1}{8}\) yardas de tela para la camisa de su hijo. ¿Cuánta tela necesita para hacer ambas playeras?
- La costura Pauline tiene\(3 \dfrac{1}{4}\) yardas de tela para hacer una chamarra. La chamarra usa\(2 \dfrac{2}{3}\) yardas. ¿Cuánta tela le quedará después de hacer la chamarra?
- Imprimir Nishant es imprimir invitaciones en su computadora. El papel mide\(8 \dfrac{1}{2}\) pulgadas de ancho y establece el área de impresión para que tenga un borde\(1 \dfrac{1}{2}\) de pulgadas en cada lado. ¿Qué tan amplia es el área de impresión en la hoja de papel?
- Enmarcando una foto Tessa compró un marco para la foto de graduación de su hijo. La imagen mide 8 pulgadas de ancho. El marco de fotos tiene\(2 \dfrac{5}{8}\) pulgadas de ancho en cada lado. ¿Qué tan amplia será la imagen enmarcada?
Ejercicios de escritura
- Dibuja un diagrama y úsalo para explicar cómo agregar\(1 \dfrac{5}{8} + 2 \dfrac{7}{8}\).
- Edgar tendrá que pagar $3.75 en peajes para conducir a la ciudad.
- Explique cómo puede hacer cambios desde una factura de $10 antes de irse para que tenga la cantidad exacta que necesita.
- ¿Cómo es similar la situación de Edgar a cómo restas 10 −\(3 \dfrac{3}{4}\)?
- Agrega\(4 \dfrac{5}{12} + 3 \dfrac{7}{8}\) dos veces, primero dejándolos como números mixtos y luego reescribiendo como fracciones inadecuadas. ¿Qué método prefieres y por qué?
- Restar\(3 \dfrac{7}{8} − 4 \dfrac{5}{12}\) dos veces, primero dejándolos como números mixtos y luego reescribiendo como fracciones impropias. ¿Qué método prefieres y por qué?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
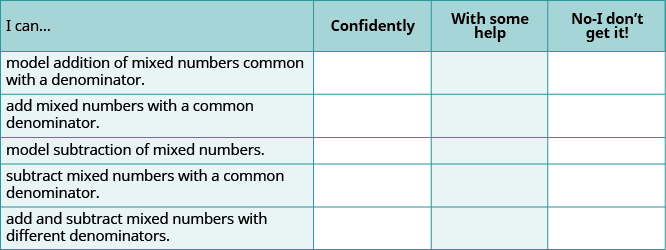
(b) Después de revisar esta lista de verificación, ¿qué hará para tener confianza en todos los objetivos?


