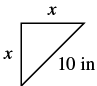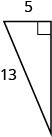9.5: Propiedades de Uso de Ángulos, Triángulos y Teorema de Pitágoras (Parte 2)
- Page ID
- 114186
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa el Teorema de Pitágoras
El Teorema de Pitágoras es una propiedad especial de los triángulos rectos que se ha utilizado desde la antigüedad. Lleva el nombre del filósofo y matemático griego Pitágoras que vivió alrededor del 500 a.C.
Recuerda que un triángulo rectángulo tiene un ángulo de 90°, que solemos marcar con un pequeño cuadrado en la esquina. El lado del triángulo opuesto al ángulo de 90° se llama hipotenusa, y los otros dos lados se llaman las piernas. Ver Figura\(\PageIndex{8}\).
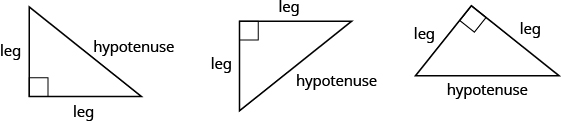
Figura\(\PageIndex{8}\) - En un triángulo rectángulo, el lado opuesto al ángulo de 90° se llama hipotenusa y a cada uno de los otros lados se le llama pierna.
El Teorema de Pitágoras cuenta cómo las longitudes de los tres lados de un triángulo rectángulo se relacionan entre sí. Afirma que en cualquier triángulo rectángulo, la suma de los cuadrados de las dos patas es igual al cuadrado de la hipotenusa.
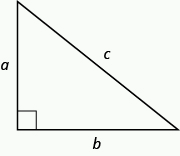
En cualquier triángulo rectángulo ΔABC,
\[a^{2} + b^{2} = c^{2}\]
donde c es la longitud de la hipotenusa a y b son las longitudes de las piernas.
Para resolver problemas que utilicen el Teorema de Pitágoras, necesitaremos encontrar raíces cuadradas. En Simplificar y Usar Raíces Cuadradas introdujimos la notación m y la definimos de esta manera:
\[If\; m = n^{2}, then\; \sqrt{m} = n\; for\; n \geq 0\]
Por ejemplo, encontramos que\(\sqrt{25}\) es 5 porque 5 2 = 25.
Utilizaremos esta definición de raíces cuadradas para resolver por la longitud de un lado en un triángulo rectángulo.
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
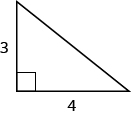
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | la longitud de la hipotenusa del triángulo |
| Paso 3. Nombre. Elija una variable para representarla. |
Let c = la longitud de la hipotenusa
|
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. | $$\ begin {split} a^ {2} + b^ {2} &= c^ {2}\\ 3^ {2} + 4^ {2} &= c^ {2}\ end {split} $$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} 9 + 16 &= c^ {2}\\ 25 &= c^ {2}\\\ sqrt {25} &= c^ {2}\\ 5 &= c\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 3^ {2} + 4^ {2} &=\ textcolor {rojo} {5} ^ {2}\\ 9 + 16 &\ stackrel {?} {=} 25\\ 25 &= 25\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | La longitud de la hipotenusa es de 5. |
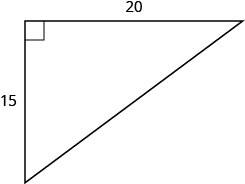
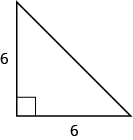
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
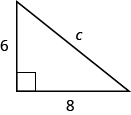
- Responder
-
c = 10
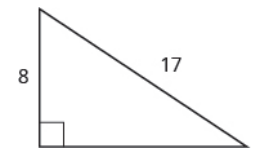
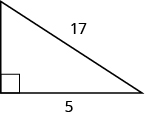
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
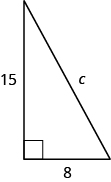
- Responder
-
c = 17
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna más larga.
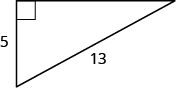
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | La longitud de la pata del triángulo |
| Paso 3. Nombre. Elija una variable para representarla. |
Let b = la pata del triángulo Lado de la etiqueta b
|
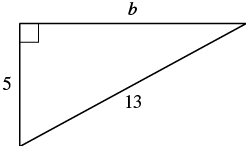
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. | $$\ begin {split} a^ {2} + b^ {2} &= c^ {2}\\ 5^ {2} + b^ {2} &= 13^ {2}\ end {split} $$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} 25 + b^ {2} &= 169\\ b^ {2} &= 144\\ b^ {2} &=\ sqrt {144}\\ b &= 12\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 5^ {2} +\ textcolor {rojo} {12} ^ {2} &\ stackrel {?} {=} 13^ {2}\\ 25 + 144 &\ stackrel {?} {=} 169\\ 169 &= 169\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | La longitud de la pierna es de 12. |
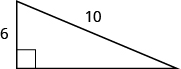
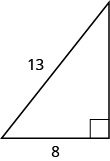
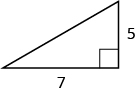
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna.
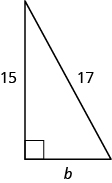
- Responder
-
b = 8
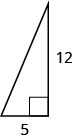
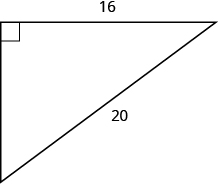
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna.
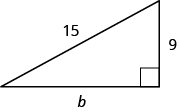
- Responder
-
b = 12
Kelvin está construyendo una glorieta y quiere encordar cada esquina colocando un soporte de madera de 10 pulgadas en diagonal como se muestra. ¿A qué distancia por debajo de la esquina debe sujetar el soporte si quiere que las distancias de la esquina a cada extremo del soporte sean iguales? Aproximado a la décima de pulgada más cercana.
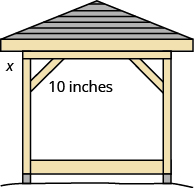
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | la distancia desde la esquina a la que se debe unir el soporte |
| Paso 3. Nombre. Elija una variable para representarla. |
Let x = la distancia desde la esquina
|
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. | $$\ begin {split} a^ {2} + b^ {2} &= c^ {2}\\ x^ {2} + x^ {2} &= 10^ {2}\ end {split} $$ |
| Paso 5. Resuelve la ecuación. Aísle la variable. Usa la definición de la raíz cuadrada. Simplificar. Aproximado a la décima más cercana. | $$\ begin {split} 2x^ {2} &= 100\\ x^ {2} &= 50\\ x &=\ sqrt {50}\\ b &\ aprox 7.1\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} a^ {2} + b^ {2} &= c^ {2}\\ (\ textcolor {rojo} {7.1}) ^ {2} + (\ textcolor {rojo} {7.1}) ^ {2} &\ stackrel {?} {\ approx} 10^ {2}\\ &Sí. \ end {split} $$ |
| Paso 7. Contesta la pregunta. | Kelvin debe sujetar cada pieza de madera aproximadamente a 7.1" de la esquina. |
John pone la base de una escalera de 13 pies a 5 pies de la pared de su casa. ¿A qué distancia de la pared llega la escalera?

- Responder
-
12 pies
Randy quiere colocar una cadena de luces de 17 pies a la parte superior del mástil de 15 pies de su velero. ¿A qué distancia de la base del mástil debe sujetar el extremo de la cuerda de luz?
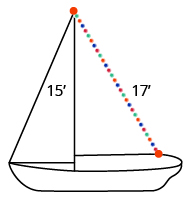
- Responder
-
8 pies
La práctica hace la perfección
Usar las propiedades de los ángulos
En los siguientes ejercicios, encuentra (a) el suplemento y (b) el complemento del ángulo dado.
- 53°
- 16°
- 29°
- 72°
En los siguientes ejercicios, usa las propiedades de los ángulos para resolver.
- Encuentra el suplemento de un ángulo de 135°.
- Encuentra el complemento de un ángulo de 38°.
- Encuentra el complemento de un ángulo de 27.5°.
- Encuentra el suplemento de un ángulo de 109.5°.
- Dos ángulos son suplementarios. El ángulo más grande es 56° más que el ángulo más pequeño. Encuentra las medidas de ambos ángulos.
- Dos ángulos son suplementarios. El ángulo más pequeño es 36° menor que el ángulo más grande. Encuentra las medidas de ambos ángulos.
- Dos ángulos son complementarios. El ángulo más pequeño es 34° menos que el ángulo más grande. Encuentra las medidas de ambos ángulos.
- Dos ángulos son complementarios. El ángulo más grande es 52° más que el ángulo más pequeño. Encuentra las medidas de ambos ángulos.
Utilizar las propiedades de los triángulos
En los siguientes ejercicios, resuelve usando propiedades de triángulos.
- Las medidas de dos ángulos de un triángulo son 26° y 98°. Encuentra la medida del tercer ángulo.
- Las medidas de dos ángulos de un triángulo son 61° y 84°. Encuentra la medida del tercer ángulo.
- Las medidas de dos ángulos de un triángulo son 105° y 31°. Encuentra la medida del tercer ángulo.
- Las medidas de dos ángulos de un triángulo son 47° y 72°. Encuentra la medida del tercer ángulo.
- Un ángulo de un triángulo rectángulo mide 33°. ¿Cuál es la medida del otro ángulo?
- Un ángulo de un triángulo rectángulo mide 51°. ¿Cuál es la medida del otro ángulo?
- Un ángulo de un triángulo rectángulo mide 22.5°. ¿Cuál es la medida del otro ángulo?
- Un ángulo de un triángulo rectángulo mide 36.5°. ¿Cuál es la medida del otro ángulo?
- Los dos ángulos más pequeños de un triángulo rectángulo tienen medidas iguales. Encuentra las medidas de los tres ángulos.
- La medida del ángulo más pequeño de un triángulo rectángulo es 20° menos que la medida del otro ángulo pequeño. Encuentra las medidas de los tres ángulos.
- Los ángulos en un triángulo son tales que la medida de un ángulo es el doble de la medida del ángulo más pequeño, mientras que la medida del tercer ángulo es tres veces la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Los ángulos en un triángulo son tales que la medida de un ángulo es 20° más que la medida del ángulo más pequeño, mientras que la medida del tercer ángulo es tres veces la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
Encuentra la longitud del lado faltante
En los siguientes ejercicios, Δ ABC es similar a Δ XYZ. Encuentra la longitud del lado indicado.
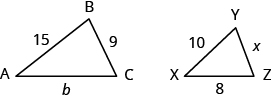
- lado b
- lado x
En un mapa, San Francisco, Las Vegas y Los Ángeles forman un triángulo cuyos lados se muestran en la siguiente figura. La distancia real de Los Ángeles a Las Vegas es de 270 millas.
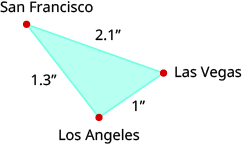
- Encuentra la distancia de Los Ángeles a San Francisco.
- Encuentra la distancia de San Francisco a Las Vegas.
Usa el Teorema de Pitágoras
En los siguientes ejercicios, utilice el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
Encuentra la longitud del lado faltante
En los siguientes ejercicios, usa el Teorema de Pitágoras para encontrar la longitud del lado faltante. Redondear a la décima más cercana, si es necesario.
En los siguientes ejercicios, resuelve. Aproximado a la décima más cercana, si es necesario.
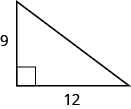
- Una cadena de luces de 13 pies se colocará en la parte superior de un poste de 12 pies para una exhibición navideña. ¿A qué distancia de la base del poste se debe anclar el extremo de la cadena de luces?
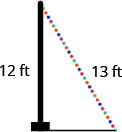
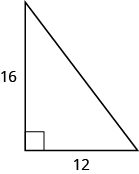
- Pam quiere poner una pancarta en la puerta de su cochera para felicitar a su hijo por su graduación universitaria. La puerta del garaje es de 12 pies de alto y 16 pies de ancho. ¿Cuánto tiempo debe ser la pancarta para que se ajuste a la puerta del garaje?

- Chi planea poner un camino de adoquines a través de su jardín de flores. El jardín de flores es un cuadrado con lados de 10 pies. ¿Cuál será la longitud del camino?
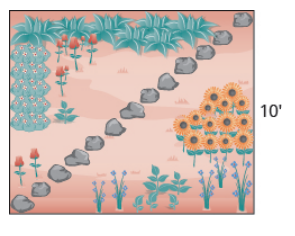
- Brian tomó prestada una escalera de extensión de 20 pies para pintar su casa. Si pone la base de la escalera a 6 pies de la casa, ¿a qué distancia llegará la parte superior de la escalera?

Matemáticas cotidianas
- Construyendo una maqueta Joe quiere construir una casa de muñecas para su hija. Quiere que la casa de muñecas se vea igual que su casa. Su casa mide 30 pies de ancho y 35 pies de alto en el punto más alto del techo. Si la casa de muñecas tendrá 2.5 pies de ancho, ¿qué tan alto será su punto más alto?
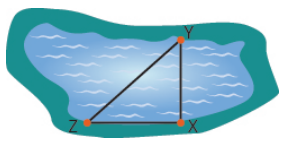
- Medición Un ingeniero de la ciudad planea construir una pasarela a través de un lago desde el punto X hasta el punto Y, como se muestra en la imagen de abajo. Para encontrar la longitud de la pasarela, dibuja un triángulo rectángulo XYZ, con ángulo recto en X. Mide la distancia de X a Z, 800 pies, y de Y a Z, 1,000 pies. ¿Cuánto durará el puente?
Ejercicios de escritura
- Escribe tres de las propiedades de los triángulos de esta sección y luego explica cada una con tus propias palabras.
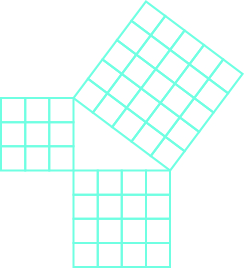
- Explique cómo la siguiente figura ilustra el Teorema de Pitágoras para un triángulo con patas de longitud 3 y 4.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?