1.1.6: Escalado y Área

Lección

Construyamos formas escaladas e investiguemos sus áreas.

Ejercicio\(\PageIndex{1}\): Scaling a Pattern Block

Usa los applets para explorar los bloques de patrones. Trabaje con su grupo para construir las copias escaladas descritas en cada pregunta.

Figura\(\PageIndex{1}\)

1. ¿Cuántos bloques de rombo azul se necesita para construir una copia a escala de la Figura A?
   1. ¿Dónde cada lado es el doble de largo?
   2. ¿Dónde cada lado es 3 veces más largo?
   3. ¿Dónde cada lado es 4 veces más largo?
2. ¿Cuántos bloques triangulares verdes se necesita para construir una copia a escala de la Figura B?
   1. ¿Dónde cada lado es el doble de largo?
   2. ¿Dónde cada lado es 3 veces más largo?
   3. ¿Usando un factor de escala de 4?
3. ¿Cuántos bloques trapezoidales rojos se necesita para construir una copia a escala de la Figura C?
   1. ¿Usando un factor de escala de 2?
   2. ¿Usando un factor de escala de 3?
   3. ¿Usando un factor de escala de 4?
4. Haz una predicción: ¿Cuántos bloques se necesitarían para construir copias escaladas de estas formas usando un factor de escala de 5? ¿Usando un factor de escala de 6? Esté preparado para explicar su razonamiento.

Ejercicio\(\PageIndex{2}\): Scaling More Pattern Blocks

Tu profesor asignará a tu grupo una de estas figuras, cada una hecha con bloques de tamaño original.

Figura\(\PageIndex{2}\): 3 formas compuestas por bloques patrón. Primera forma, etiquetada figura D compuesta por 3 rombos azules. Segundo, etiquetada figura E compuesta por 2 trapecios rojos. Tercero, etiquetada figura F compuesta por 4 triángulos verdes.

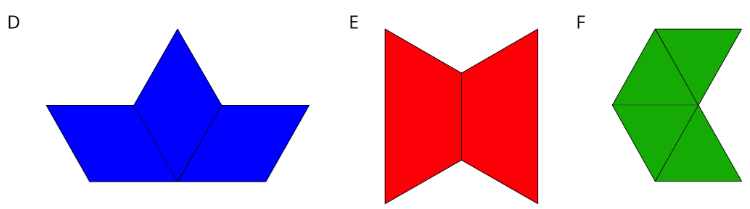
1. En el applet, mueve el control deslizante para ver una copia a escala de tu forma asignada, usando un factor de escala de 2. Usa los bloques de tamaño original para construir una figura que coincida con ella. ¿Cuántas cuadras tomó?
2. Tu compañero piensa que las copias escaladas en el problema anterior tardarán 4 bloques cada una en construirse. ¿Estás de acuerdo o en desacuerdo? Explícale razonamiento.
3. Mueve el control deslizante para ver una copia a escala de tu forma asignada usando un factor de escala de 3. Comienza a construir una figura con los bloques de tamaño original para que coincida con ella. Detente cuando puedas saber con certeza cuántos bloques tomaría. Registre su respuesta.
4. Predecir: ¿Cuántos bloques se necesitarían para construir copias escaladas usando los factores de escala 4, 5 y 6? Explica o muestra tu razonamiento.
5. ¿Cómo es el patrón en esta actividad el mismo que el patrón que viste en la actividad anterior? ¿En qué se diferencia?

¿Estás listo para más?

1. ¿Cuántos bloques crees que se necesitarían para construir una copia a escala de un hexágono amarillo donde cada lado es el doble de largo? ¿Tres veces más?
2. Encuentra una manera de construir estas copias escaladas.
3. ¿Ves un patrón para el número de bloques utilizados para construir estas copias escaladas? Explica tu razonamiento.

Ejercicio\(\PageIndex{3}\): Area of Scaled Parallelograms and Triangles

1. Tu profesor te dará una figura con medidas en centímetros. ¿Cuál es el área de tu figura? ¿Cómo lo sabes?
2. Trabaja con tu pareja para dibujar copias a escala de tu figura, usando cada factor de escala de la tabla. Completa la tabla con las medidas de tus copias escaladas.

   Mesa\(\PageIndex{1}\)

   factor de escala	base (cm)	altura (cm)	área (cm ^2)
   \(1\)
   \(2\)
   \(3\)
   \(\frac{1}{2}\)
   \(\frac{1}{3}\)

3. Compara tus resultados con un grupo que trabajó con una figura diferente. ¿Qué es lo mismo de tus respuestas? ¿Qué es diferente?
4. Si dibujaste copias a escala de tu figura con los siguientes factores de escala, ¿cuáles serían sus áreas? Discuta tu pensamiento. Si no estás de acuerdo, trabaja para llegar a un acuerdo. Esté preparado para explicar su razonamiento.

Mesa\(\PageIndex{2}\)

factor de escala	área (cm ^2)
\(5\)
\(\frac{3}{5}\)

Resumen

La escala afecta a longitudes y áreas de manera diferente. Cuando hacemos una copia a escala, todas las longitudes originales se multiplican por el factor de escala. Si hacemos una copia de un rectángulo con longitudes laterales 2 unidades y 4 unidades usando un factor de escala de 3, las longitudes laterales de la copia serán 6 unidades y 12 unidades, porque\(2\cdot 3=6\) y\(4\cdot 3=12\).

Figura\(\PageIndex{3}\)

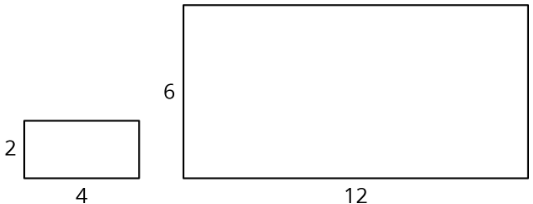
El área de la copia, sin embargo, cambia por un factor de (factor de escala) ². Si cada longitud lateral de la copia es 3 veces mayor que la longitud lateral original, entonces el área de la copia será 9 veces el área del original, porque, o\(3\cdot 3\)\(3^{2}\), es igual a 9.

Figura\(\PageIndex{4}\): Dos rectángulos. El primer rectángulo tiene el lado vertical etiquetado 2 y el lado horizontal etiquetado 4. El segundo rectángulo tiene el lado vertical etiquetado 6 y el lado horizontal etiquetado 12. Dos líneas discontinuas horizontales y 2 líneas discontinuas verticales se dibujan en el segundo rectángulo dividiéndolo en 9 rectángulos idénticos más pequeños.

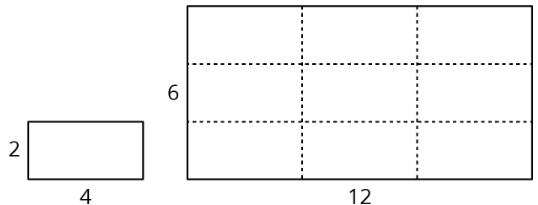
En este ejemplo, el área del rectángulo original es de 8 unidades ² y el área de la copia a escala es de 72 unidades ², porque\(9\cdot 8=72\). Podemos ver que el rectángulo grande está cubierto por 9 copias del rectángulo pequeño, sin huecos ni superposiciones. También podemos verificar esto multiplicando las longitudes laterales del rectángulo grande:\(6\cdot 12=72\).

Las longitudes son unidimensionales, por lo que en una copia a escala, cambian por el factor de escala. El área es bidimensional, por lo que cambia por el cuadrado del factor de escala. Podemos ver que esto es cierto para un rectángulo con largo\(l\) y ancho\(w\). Si escalamos el rectángulo por un factor de escala de\(s\), obtenemos un rectángulo con largo\(s\cdot l\) y ancho\(s\cdot w\). El área del rectángulo escalado es\(A=(s\cdot l)\cdot (s\cdot w)\), entonces\(A=(s^{2})\cdot (l\cdot w)\). El hecho de que el área se multiplica por el cuadrado del factor de escala también es cierto para copias escaladas de otras figuras bidimensionales, no solo para rectángulos.

Entradas en el glosario

Definición: Área

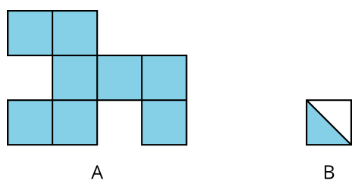
Área es el número de unidades cuadradas que cubren una región bidimensional, sin huecos ni superposiciones.

Por ejemplo, el área de la región A es de 8 unidades cuadradas. El área de la región sombreada de B es unidad\(\frac{1}{2}\) cuadrada.

Figura\(\PageIndex{5}\)

Definición: Correspondiente

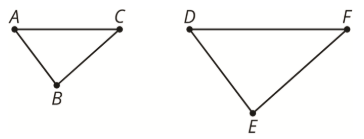
Cuando parte de una figura original coincide con parte de una copia, las llamamos partes correspondientes. Estos podrían ser puntos, segmentos, ángulos o distancias.

Por ejemplo, el punto\(B\) en el primer triángulo corresponde al punto\(E\) en el segundo triángulo. Segmento\(AC\) corresponde al segmento\(DF\).

Figura\(\PageIndex{6}\)

Definición: Recíproco

Dividir 1 por un número da el recíproco de ese número. Por ejemplo, el recíproco de 12 es\(\frac{1}{12}\), y el recíproco de\(\frac{2}{5}\) es\(\frac{5}{2}\).

Definición: Factor de Escala

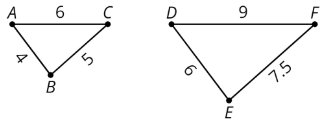
Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Este número se llama factor de escala.

En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).

Figura\(\PageIndex{7}\)

Definición: Copia escalada

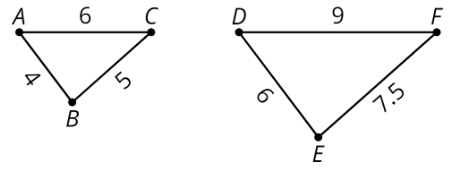
Una copia a escala es una copia de una figura donde cada longitud de la figura original se multiplica por el mismo número.

Por ejemplo, triángulo\(DEF\) es una copia a escala de triángulo\(ABC\). Cada longitud de lado en triángulo\(ABC\) se multiplicó por 1.5 para obtener la longitud de lado correspondiente en triángulo\(DEF\).

Figura\(\PageIndex{8}\)

Práctica

Ejercicio\(\PageIndex{4}\)

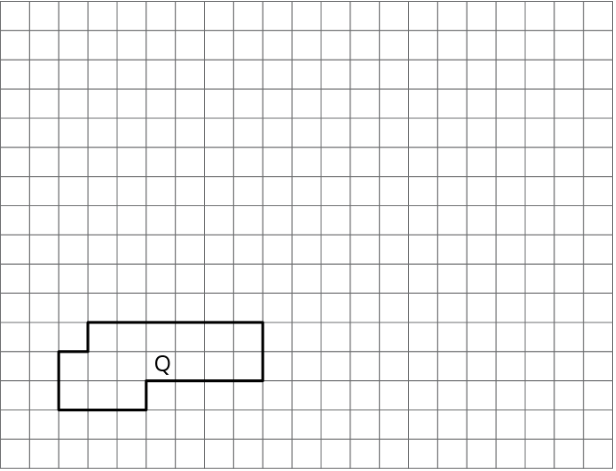
En la cuadrícula, dibuje una copia escalada del Polígono Q usando un factor de escala de 2. Comparar el perímetro y el área del nuevo polígono con los de Q.

Figura\(\PageIndex{9}\): Un polígono alineado a una cuadrícula cuadrada está etiquetado Q. La forma está compuesta por 3 rectángulos. La parte izquierda de la forma es de 2 cuadrados de alto y 1 cuadrado de ancho. La siguiente parte de la forma es de 3 cuadrados de alto y 2 cuadrados de ancho. La siguiente parte de la forma comienza 1 cuadrado hacia arriba desde la parte inferior de la forma y tiene 2 cuadrados de alto por 4 cuadrados de ancho.

Ejercicio\(\PageIndex{5}\)

Un triángulo rectángulo tiene una superficie de 36 unidades cuadradas.

Si dibujas copias a escala de este triángulo usando los factores de escala de la tabla, ¿cuáles serán las áreas de estas copias escaladas? Explica o muestra tu razonamiento.

Mesa\(\PageIndex{3}\)

factor de escala	área (unidades ^2)
\(1\)	\(36\)
\(2\)
\(3\)
\(5\)
\(\frac{1}{2}\)
\(\frac{2}{3}\)

Ejercicio\(\PageIndex{6}\)

Diego dibujó una versión a escala de un Polígono P y lo etiquetó Q.

Figura\(\PageIndex{10}\): Un polígono alineado a una cuadrícula cuadrada etiquetada Q. El polígono se compone de 4 formas, unidas entre sí a lo largo de sus bordes. A la izquierda hay un triángulo rectángulo con una base de 1 unidad y una altura de 2 unidades. A la derecha del triángulo hay un rectángulo de 2 unidades por 1 unidad alineado con su lado de 2 unidades junto al lado de 2 unidades del triángulo. A la derecha de ésta hay un cuadrado de 1 unidad, encima de un triángulo de media unidad.

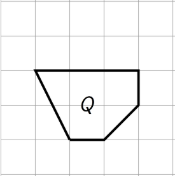
Si el área del Polígono P es de 72 unidades cuadradas, ¿qué factor de escala utilizó Diego para pasar de P a Q? Explica tu razonamiento.

Ejercicio\(\PageIndex{7}\)

Aquí hay un polígono sin etiquetar, junto con sus copias escaladas Polígonos A-D. Para cada copia, determine el factor de escala. Explica cómo sabes.

Figura\(\PageIndex{11}\): Polígono de cuatro lados sin etiquetar con cuatro copias a escala diferentes etiquetadas A, B, C y D en una cuadrícula cuadrada. El polígono no etiquetado tiene 4 lados, con una altura vertical de 2 en el lado izquierdo. La altura del lado vertical en cada polígono es la siguiente: Polígono A: 1 unidad. Polígono B: 4 unidades. Polígono C: 3 unidades. Polígono D: 2 unidades.

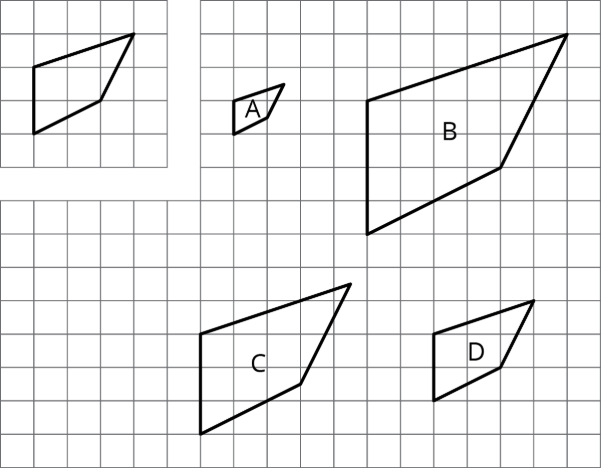
(De la Unidad 1.1.2)

Ejercicio\(\PageIndex{8}\)

Resuelve cada ecuación mentalmente.

1. \(\frac{1}{7}\cdot x=1\)
2. \(x\cdot\frac{1}{11}=1\)
3. \(1\div\frac{1}{5}=x\)

(De la Unidad 1.1.5)