Saltar al contenido principal
LibreTexts Español

1.1.5: El tamaño del factor de escala

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119233

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Veamos los efectos de diferentes factores de escala.

    Ejercicio\(\PageIndex{1}\): Number Talk: Missing Factor

    Resuelve cada ecuación mentalmente.

    \(16x=176\)

    \(16x=8\)

    \(16x=1\)

    \(\frac{1}{5}x=1\)

    \(\frac{2}{5}x=1\)

    Ejercicio\(\PageIndex{2}\): Card Sort: Scaled Copies

    Tu profesor te dará un juego de tarjetas. En cada tarjeta, la Figura A es el original y la Figura B es una copia a escala.

    1. Clasifique las tarjetas en función de sus factores de escala. Esté preparado para explicar su razonamiento.
    2. Examine más de cerca las tarjetas 10 y 13. ¿Qué notas sobre las formas y tamaños de las figuras? ¿Qué notas sobre los factores de escala?
    3. Examine más de cerca las tarjetas 8 y 12. ¿Qué notas de las cifras? ¿Qué notas sobre los factores de escala?

    ¿Estás listo para más?

    El Triángulo B es una copia a escala del Triángulo A con factor de escala\(\frac{1}{2}\).

    1. ¿Cuántas veces más grandes son las longitudes laterales del Triángulo B en comparación con el Triángulo A?
    2. Imagina que escalas el Triángulo B por un factor de escala de\(\frac{1}{2}\) para obtener el Triángulo C. ¿Cuántas veces mayores serán las longitudes laterales del Triángulo C en comparación con el Triángulo A?
    3. El triángulo B se ha escalado una vez. El triángulo C se ha escalado dos veces. Imagina que escalas triángulo A\(n\) veces para obtener Triángulo N, siempre usando un factor de escala de\(\frac{1}{2}\). ¿Cuántas veces mayores serán las longitudes laterales del Triángulo N en comparación con el Triángulo A?

    Ejercicio\(\PageIndex{3}\): Scaling A Puzzle

    Tu profesor te dará 2 piezas de un rompecabezas de 6 piezas.

    1. Si dibujaste copias a escala de tus piezas del rompecabezas usando un factor de escala de\(\frac{1}{2}\), ¿serían más grandes o más pequeñas que las piezas originales? ¿Cómo lo sabes?

    2. Crea una copia a escala de cada pieza del rompecabezas en un cuadrado en blanco, con un factor de escala de\(\frac{1}{2}\).

    3. Cuando todos en tu grupo hayan terminado, junta las 6 piezas originales del rompecabezas así:

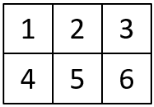
    clipboard_ee672fdc1f7d4cb06907f82fe19077661.png
    Figura\(\PageIndex{1}\)

    A continuación, junte las 6 copias a escala. Compara tu rompecabezas a escala con el rompecabezas original. ¿Qué partes parecen estar escaladas correctamente y cuáles parecen apagadas? ¿Qué pudo haber causado que esas partes se apagaran?

    4. Revisar cualquiera de las copias a escala que puedan haber sido dibujadas incorrectamente.

    5. Si tuvieras que perder una de las piezas del rompecabezas original, pero aún así tenías la copia a escala, ¿cómo podrías recrear la pieza perdida?

    Ejercicio\(\PageIndex{4}\): Missing Figure, Factor, or Copy

    1. ¿Cuál es el factor de escala desde el triángulo original hasta su copia? Explica o muestra tu razonamiento.

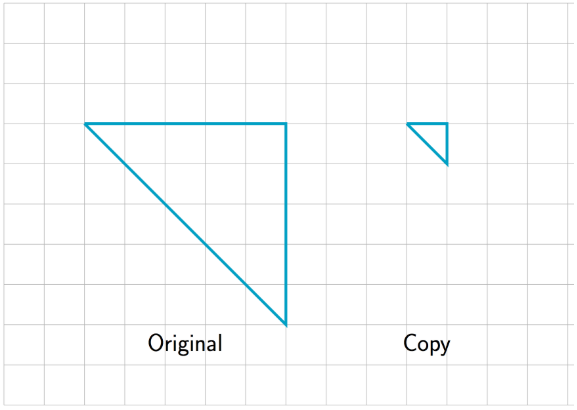
    clipboard_e681998173320ef143df3562bfa15f729.png
    Figura\(\PageIndex{2}\)

    2. El factor de escala desde el trapecio original hasta su copia es 2. Dibuja la copia a escala.

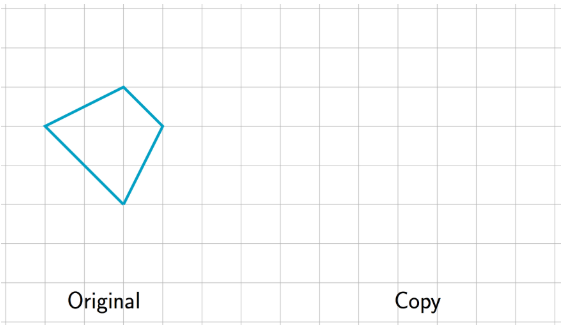
    clipboard_e5755261fd27229a0253f68f9574c05a8.png
    Figura\(\PageIndex{3}\)

    3. El factor de escala desde la figura original hasta su copia es\(\frac{3}{2}\). Dibuja la figura original.

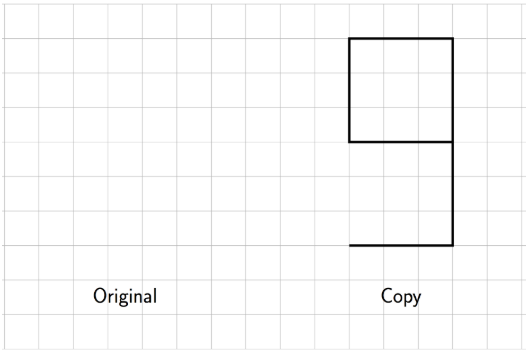
    clipboard_ec7423752397e02780a0bf81851e05335.png
    Figura\(\PageIndex{4}\)

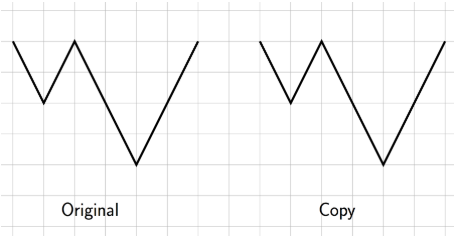
    4. ¿Cuál es el factor de escala desde la figura original hasta la copia? Explique cómo sabe.

    clipboard_e6761ab1e634c587a883367578e8a0191.png
    Figura\(\PageIndex{5}\)

    5. El factor de escala desde la figura original hasta su copia escalada es 3. Dibuja la copia a escala.

    clipboard_eff2036d9a8f518dd92506d5e7bd4a455.png
    Figura\(\PageIndex{6}\): Un triángulo con el lado horizontal extendido hacia la derecha y el lado vertical extendido hacia arriba creando una figura que se asemeja al número 4. La figura está etiquetada como original. A la derecha, la posición etiquetada copia está en blanco.

    Resumen

    El tamaño del factor de escala afecta el tamaño de la copia. Cuando una figura se escala por un factor de escala mayor que 1, la copia es mayor que la original. Cuando el factor de escala es menor que 1, la copia es menor. Cuando el factor de escala es exactamente 1, la copia tiene el mismo tamaño que el original.

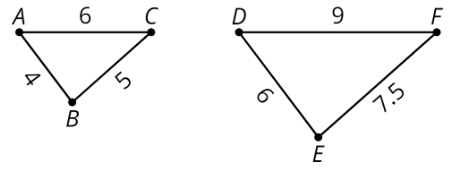
    Triángulo\(DEF\) es una copia de triángulo a mayor escala\(ABC\), porque el factor de escala de\(ABC\) a\(DEF\) es\(\frac{3}{2}\). Triángulo\(ABC\) es una copia de triángulo a menor escala\(DEF\), porque el factor de escala de\(DEF\) a\(ABC\) es\(\frac{2}{3}\).

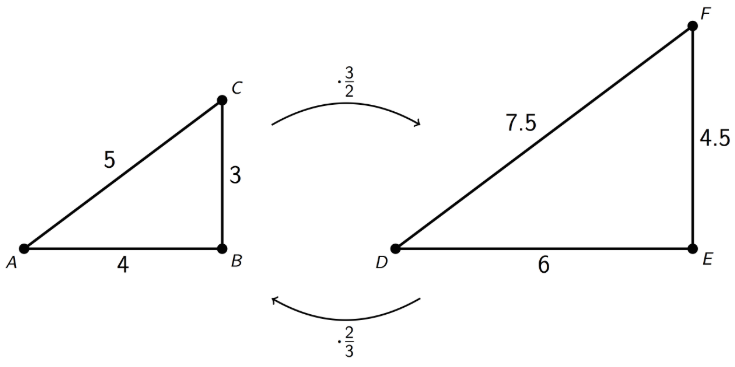
    clipboard_eba5fbe7b5fb9bacd3c08a63d798381a9.png
    Figura\(\PageIndex{7}\): Dos triángulos; uno etiquetado A B C con horizontal A B y el otro D E F con horizontal D E. La longitud de A B está etiquetada con 4. La longitud de B C está etiquetada con 3. La longitud de C A está etiquetada como 5. La longitud de D E está etiquetada con 6. La longitud de E F está etiquetada con 4.5. La longitud de F D está etiquetada con 7.5. Una flecha del triángulo A B C que apunta al triángulo D E F está etiquetada, multiplicada por 3 mitades. Una flecha del triángulo D E F que apunta al triángulo A B C está etiquetada por 2 tercios.

    Esto significa que los triángulos\(ABC\) y\(DEF\) son copias escaladas entre sí. También muestra que el escalado se puede revertir utilizando factores de escala recíprocos, como\(\frac{2}{3}\) y\(\frac{3}{2}\).

    En otras palabras, si escalamos la Figura A usando un factor de escala de 4 para crear la Figura B, podemos escalar la Figura B usando el factor de escala recíproco,\(\frac{1}{4}\), para crear la Figura A.

    Entradas en el glosario

    Definición: Correspondiente

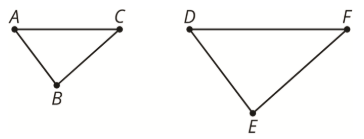
    Cuando parte de una figura original coincide con parte de una copia, las llamamos partes correspondientes. Estos podrían ser puntos, segmentos, ángulos o distancias.

    Por ejemplo, el punto\(B\) en el primer triángulo corresponde al punto\(E\) en el segundo triángulo. Segmento\(AC\) corresponde al segmento\(DF\).

    clipboard_e2728b3247bf3bb939a001aa3dc3bac53.png
    Figura\(\PageIndex{8}\)

    Definición: Recíproco

    Dividir 1 por un número da el recíproco de ese número. Por ejemplo, el recíproco de 12 es\(\frac{1}{12}\), y el recíproco de\(\frac{2}{5}\) es\(\frac{5}{2}\).

    Definición: Factor de Escala

    Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. A este número se le llama factor de escala.

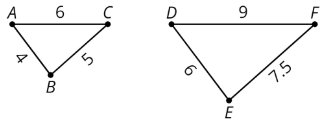
    En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).

    clipboard_e919f0ad3848582ce451f8d8df95d9f1e.png
    Figura\(\PageIndex{9}\)

    Definición: Copia escalada

    Una copia a escala es una copia de una figura donde cada longitud de la figura original se multiplica por el mismo número.

    Por ejemplo, triángulo\(DEF\) es una copia a escala de triángulo\(ABC\). Cada longitud de lado en triángulo\(ABC\) se multiplicó por 1.5 para obtener la longitud de lado correspondiente en triángulo\(DEF\).

    clipboard_e7a834304f2fbd754976975695baf4ec5.png
    Figura\(\PageIndex{10}\)

    Practica

    Ejercicio\(\PageIndex{5}\)

    Los rectángulos P, Q, R y S son copias escaladas entre sí. Para cada par, decida si el factor de escala de uno a otro es mayor que 1, igual a 1, o menor que 1.

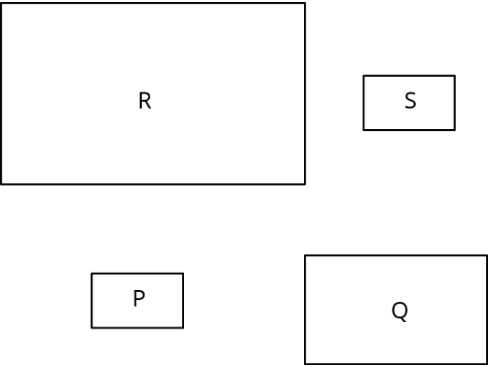
    clipboard_e3a82cd0ffdc66d711a54e3f0ac9ccded.png
    Figura\(\PageIndex{11}\): Cuatro rectángulos, etiquetados P, Q, R y S. Cada rectángulo es una copia a escala uno del otro. Clasificado en orden de menor a mayor, el área de los rectángulos son los siguientes: el área de P es igual a S, que son menores que el área de Q, que es menor que el área de R.
    1. de P a Q
    2. de P a R
    3. de Q a S
    4. de Q a R
    5. de S a P
    6. de R a P
    7. de P a S

    Ejercicio\(\PageIndex{6}\)

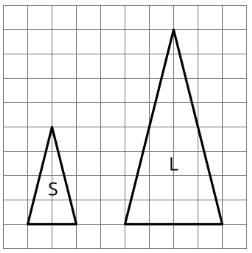
    El Triángulo S y el Triángulo L son copias escaladas entre sí.

    1. ¿Cuál es el factor de escala de S a L?
    2. ¿Cuál es el factor de escala de L a S?
    3. El triángulo M también es una copia a escala de S. El factor de escala de S a M es\(\frac{3}{2}\). ¿Cuál es el factor de escala de M a S?
    clipboard_e4daaaedac66149ff8959571a3ebaa306.png
    Figura\(\PageIndex{12}\)

    Ejercicio\(\PageIndex{7}\)

    ¿Dos cuadrados con las mismas longitudes laterales son copias escaladas entre sí? Explica tu razonamiento.

    Ejercicio\(\PageIndex{8}\)

    El cuadrilátero A tiene longitudes laterales 2, 3, 5 y 6. El cuadrilátero B tiene longitudes laterales 4, 5, 8 y 10. ¿Podría uno de los cuadriláteros ser una copia a escala del otro? Explique.

    (De la Unidad 1.1.2)

    Ejercicio\(\PageIndex{9}\)

    Seleccione todas las proporciones que sean equivalentes a la proporción\(12:3\)

    1. \(6:1\)
    2. \(1:4\)
    3. \(4:1\)
    4. \(24:6\)
    5. \(15:6\)
    6. \(1,200:300\)
    7. \(112:13\)

    This page titled 1.1.5: El tamaño del factor de escala is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.