2.2.1: Relaciones proporcionales y ecuaciones
- Page ID
- 119150
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Escribamos ecuaciones que describan las relaciones proporcionales.
Ejercicio\(\PageIndex{1}\): NUmber Talk: Division
Encuentra cada cociente mentalmente.
\(645\div 100\)
\(645\div 50\)
\(48.6\div 30\)
\(48.6\div x\)
Ejercicio\(\PageIndex{2}\): Feeding a Crowd, Revisited
1. Una receta dice que 2 tazas de arroz seco servirán a 6 personas. Completa la tabla mientras respondes las preguntas. Esté preparado para explicar su razonamiento.
- ¿Cuántas personas servirán 1 taza de arroz?
- ¿Cuántas personas servirán 3 tazas de arroz? ¿12 tazas? ¿43 tazas?
- ¿Cuántas personas servirán\(x\) tazas de arroz?
| tazas de arroz seco | número de personas |
|---|---|
| 1 | |
| 2 | 6 |
| 3 | |
| 12 | |
| 43 | |
| \(x\) |
2. Una receta dice que 6 rollitos de primavera servirán a 3 personas. Completa la tabla mientras respondes las preguntas. Esté preparado para explicar su razonamiento.
- ¿A cuántas personas servirán 1 Rollo Primavera?
- ¿A cuántas personas servirán 10 rollitos de primavera? 16 rollitos de primavera? 25 rollitos de primavera?
- ¿A cuántas personas servirán los rollitos de\(n\) primavera?
| número de rollitos de primavera | número de personas |
|---|---|
| 1 | |
| 6 | 3 |
| 10 | |
| 16 | |
| 25 | |
| \(n\) |
3. ¿En qué se diferenciaba completar esta tabla de la tabla anterior? ¿Cómo como lo mismo?
Ejercicio\(\PageIndex{3}\): Denver to Chicago
Un avión voló a velocidad constante entre Denver y Chicago. El avión tardó 1.5 horas en volar 915 millas.
- Completa la tabla.
tiempo (horas) distancia (millas) velocidad (millas por hora) 1 1.5 915 2 2.5 \(t\) Mesa\(\PageIndex{3}\) - ¿A qué distancia vuela el avión en una hora?
- ¿Hasta dónde volaría el avión en\(t\) horas a esta velocidad?
- Si\(d\) representa la distancia que el avión vuela a esta velocidad durante\(t\) horas, escriba una ecuación que relacione\(t\) y\(d\).
- ¿Hasta dónde volaría el avión en 3 horas a esta velocidad? en 3.5 horas? Explica o muestra tu razonamiento.
¿Estás listo para más?
Un planeta rocoso orbita Próxima Centauri, una estrella que está a unos 1.3 pársecs de la Tierra. Este planeta es el planeta más cercano fuera de nuestro sistema solar.
- ¿Cuánto tiempo tarda la luz de Próxima Centauri en llegar a la Tierra? (Un pársec es de unos 3.26 años luz. Un año luz es la distancia que recorre la luz en un año.)
- Hay dos mellizos. Un gemelo sale en una nave espacial para explorar el planeta cerca de Próxima Centauri viajando al 90% de la velocidad de la luz, mientras que el otro gemelo se queda en casa en la Tierra. ¿Cuánto envejece el gemelo en la Tierra mientras el otro gemelo viaja a Próxima Centauri? (¿Crees que la respuesta sería la misma para el otro gemelo? Considera investigar “La paradoja gemela” para obtener más información.)
Ejercicio\(\PageIndex{4}\): Revisiting a Bread Dough
Una panadería utiliza 8 cucharadas de miel por cada 10 tazas de harina para hacer masa de pan. Algunos días hornean lotes más grandes y algunos días hornean lotes más pequeños, pero siempre usan la misma proporción de miel a harina.
- Completa la tabla.
- Si\(f\) son las tazas de harina necesarias para\(h\) cucharadas de miel, escribir una ecuación que relacione\(f\) y\(h\).
- ¿Cuánta harina se necesita para 15 cucharadas de miel? ¿17 cucharadas? Explica o muestra tu razonamiento.
| miel (cda) | harina (c) |
|---|---|
| 1 | |
| 8 | 10 |
| 16 | |
| 20 | |
| \(h\) |
Resumen
En la tabla se muestra la cantidad de pintura roja y azul necesaria para hacer un cierto tono de pintura púrpura, llamada Atardecer Venusiano.
Tenga en cuenta que las “partes” pueden ser cualquier unidad por volumen. Si mezclamos 3 tazas de rojo con 12 tazas de azul, obtendrás el mismo tono que si mezclamos 3 cucharaditas de rojo con 12 cucharaditas de azul.
| pintura roja (partes) | pintura azul (partes) |
|---|---|
| \(3\) | \(12\) |
| \(1\) | \(4\) |
| \(7\) | \(28\) |
| \(\frac{1}{4}\) | \(1\) |
| \(r\) | \(4r\) |
La última fila de la tabla dice que si conocemos la cantidad de pintura roja necesaria,\(r\), siempre podemos multiplicarla por 4 para encontrar la cantidad de pintura azul necesaria,\(b\), para mezclarla con ella para hacer Atardecer Venusiano. Esto lo podemos decir de manera más sucinta con la ecuación\(b=4r\). Por lo que la cantidad de pintura azul es proporcional a la cantidad de pintura roja y la constante de proporcionalidad es 4.
También podemos mirar esta relación al revés.
Si conocemos la cantidad de pintura azul necesaria,\(b\), siempre podemos multiplicarla por\(\frac{1}{4}\) para encontrar la cantidad de pintura roja necesaria,\(r\), para mezclarla con ella para hacer Atardecer Venusiano. Entonces\(r=\frac{1}{4}b\). La cantidad de pintura azul es proporcional a la cantidad de pintura roja y la constante de proporcionalidad\(\frac{1}{4}\).
| pintura azul (partes) | pintura roja (partes) |
|---|---|
| \(12\) | \(3\) |
| \(4\) | \(1\) |
| \(28\) | \(7\) |
| \(1\) | \(\frac{1}{4}\) |
| \(b\) | \(\frac{1}{4}b\) |
En general, cuando\(y\) es proporcional a\(x\), siempre podemos multiplicar\(x\) por el mismo número\(k\) —la constante de proporcionalidad— para obtener\(y\). Podemos escribir esto mucho más sucintamente con la ecuación\(y=kx\).
Practica
Ejercicio\(\PageIndex{5}\)
Un cierto techo está formado por tejas. Cada metro cuadrado de techo requiere 10.75 tejas. Rellene la tabla con los valores faltantes.
| metros cuadrados de techo | número de mosaicos |
|---|---|
| \(1\) | |
| \(10\) | |
| \(100\) | |
| \(a\) |
Ejercicio\(\PageIndex{6}\)
En un vuelo de Nueva York a Londres, un avión viaja a una velocidad constante. Una ecuación que relaciona la distancia recorrida en millas\(d\),, con el número de horas de vuelo,\(t\), es\(t=\frac{1}{500}d\). ¿Cuánto tardará el avión en recorrer 800 millas?
Ejercicio\(\PageIndex{7}\)
Cada tabla representa una relación proporcional. Para cada uno, encontrar la constante de proporcionalidad, y escribir una ecuación que represente la relación.
| \(s\) | \(P\) |
|---|---|
| \ (s\) ">\(2\) | \ (P\) ">\(8\) |
| \ (s\) ">\(3\) | \ (P\) ">\(12\) |
| \ (s\) ">\(5\) | \ (P\) ">\(20\) |
| \ (s\) ">\(10\) | \ (P\) ">\(40\) |
Constante de proporcionalidad:
Ecuación:\(P=\)
| \(d\) | \(C\) |
|---|---|
| \ (d\) ">\(2\) | \ (C\) ">\(6.28\) |
| \ (d\) ">\(3\) | \ (C\) ">\(9.42\) |
| \ (d\) ">\(5\) | \ (C\) ">\(15.7\) |
| \ (d\) ">\(10\) | \ (C\) ">\(31.4\) |
Constante de proporcionalidad:
Ecuación:\(C=\)
Ejercicio\(\PageIndex{8}\)
Un mapa de Colorado dice que la escala es de 1 pulgada a 20 millas o de 1 a 1,267,200. ¿Estas dos formas de reportar la escala son iguales? Explica tu razonamiento.
(De la Unidad 1.2.5)
Ejercicio\(\PageIndex{9}\)
Aquí hay un polígono en una cuadrícula.
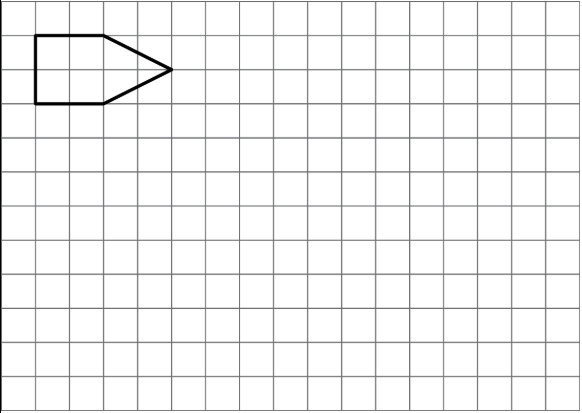
- Dibuja una copia escalada del polígono usando un factor de escala 3. Etiquetar la copia A.
- Dibuja una copia a escala del polígono con un factor de escala\(\frac{1}{2}\). Etiquetarlo B.
- ¿El Polígono A es una copia escalada del Polígono B? Si es así, ¿cuál es el factor de escala que lleva de B a A?
(De la Unidad 1.1.3)