Saltar al contenido principal
LibreTexts Español

6.1.6: Distinguir entre dos tipos de situaciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119045

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Pensemos en ecuaciones con y sin paréntesis y los tipos de situaciones que describen.

    Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Seeing Structure

    ¿Qué ecuación no pertenece?

    \(4(x+3)=9\)

    \(4\cdot x+12=9\)

    \(4+3x=9\)

    \(9=12+4x\)

    Ejercicio\(\PageIndex{2}\): Card Sort: Categories of Equations

    Tu profesor te dará un conjunto de cartas que muestran ecuaciones. Ordena las tarjetas en 2 categorías de tu elección. Esté preparado para explicar el significado de sus categorías. Después, ordena las tarjetas en 2 categorías de una manera diferente. Esté preparado para explicar el significado de sus nuevas categorías.

    Ejercicio\(\PageIndex{3}\): Even More Situations, Diagrams, and Equations

    clipboard_e16941f4b658be4a46d53d776906a6f75.png
    Figura\(\PageIndex{1}\)

    Historia 1: Lin tenía 90 volantes para colgar alrededor de la escuela. Ella entregó 12 volantes a cada uno de los tres voluntarios. Después tomó los volantes restantes y los dividió en partes iguales entre los tres voluntarios.

    Historia 2: Lin tenía 90 volantes para colgar alrededor de la escuela. Después de dar el mismo número de volantes a cada uno de los tres voluntarios, le quedaban 12 para colgar sola.

    1. ¿Qué diagrama va con qué historia? Esté preparado para explicar su razonamiento.
    2. En cada diagrama, ¿qué parte de la historia representa la variable?
    3. Escribe una ecuación correspondiente a cada historia. Si te quedas atascado, usa el diagrama.
    4. Encuentra el valor de la variable en la historia.

    ¿Estás listo para más?

    Un tutor está iniciando un negocio. En el primer año, comienzan con 5 clientes y cobran $10 por semana por una hora de tutoría con cada cliente. Para cada año siguiente, duplican el número de clientes y el número de horas cada semana. A cada nuevo cliente se le cobrará el 150% de los cargos de los clientes del año anterior.

    1. Organizar las ganancias semanales de cada año en una tabla.
    2. Asumiendo que una semana de tiempo completo es de 40 horas semanales, ¿cuántos años se tardará en llegar a tiempo completo y cuántos nuevos clientes serán contratados ese año?
    3. Después de llegar a tiempo completo, ¿cuál es el salario anual del tutor si toma 2 semanas de vacaciones?
    4. ¿Hay otro modelo de negocio que recomendarías para el tutor? Explica tu razonamiento.

    Resumen

    En esta unidad, encontramos dos tipos principales de situaciones que se pueden representar con una ecuación. Aquí hay un ejemplo de cada tipo:

    1. Después de sumar 8 estudiantes a cada uno de los 6 equipos del mismo tamaño, hubo 72 estudiantes en total.
    2. Después de agregar una caja de raquetas de tenis de 8 libras a una caja con 6 cajas idénticas de paletas de ping pong, la caja pesaba 72 libras.

    La primera situación tiene todas partes iguales, ya que se hacen adiciones a cada equipo. Una ecuación que representa esta situación es\(6(x+8)=72\), donde\(x\) representa el número original de alumnos en cada equipo. Se sumaron ocho estudiantes a cada grupo, hay 6 grupos, y hay un total de 72 estudiantes.

    En la segunda situación, hay 6 partes iguales agregadas a otra parte. Una ecuación que representa esta situación es\(6x+8=72\), donde\(x\) representa el peso de una caja de palas de ping pong, hay 6 cajas de palas de ping pong, hay una caja adicional que pesa 8 libras, y la caja pesa 72 libras en total.

    En la primera situación, hubo 6 grupos iguales, y 8 estudiantes se sumaron a cada grupo. \(6(x+8)=72\).

    En la segunda situación, hubo 6 grupos iguales, pero 8 libras más además de eso. \(6x+8=72\).

    Entradas en el glosario

    Definición: Expresiones equivalentes

    Las expresiones equivalentes son siempre iguales entre sí. Si las expresiones tienen variables, son iguales siempre que se use el mismo valor para la variable en cada expresión.

    Por ejemplo,\(3x+4x\) es equivalente a\(5x+2x\). No importa para qué valor usemos\(x\), estas expresiones son siempre iguales. Cuando\(x\) es 3, ambas expresiones equivalen a 21. Cuando\(x\) es 10, ambas expresiones equivalen a 70.

    Practica

    Ejercicio\(\PageIndex{4}\)

    Una escuela ordenó 3 cajas grandes de marcadores de tabla. Después de dar 15 marcadores a cada uno de los 3 maestros, quedaron 90 marcadores. El diagrama representa la situación. ¿Cuántos marcadores había originalmente en cada caja?

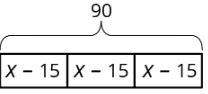
    clipboard_e54bb464bc152ee185a4567221ec3a01a.png
    Figura\(\PageIndex{2}\)

    (De la Unidad 6.1.2)

    Ejercicio\(\PageIndex{5}\)

    El diagrama puede ser representado por la ecuación\(25=2+6x\). Explica dónde puedes ver los 6 en el diagrama.

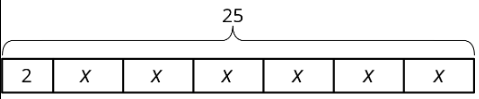
    clipboard_e22da6422656bdd322bead88c86d41a45.png
    Figura\(\PageIndex{3}\)

    (De la Unidad 6.1.3)

    Ejercicio\(\PageIndex{6}\)

    Haga coincidir cada ecuación con una historia. (Dos de las historias coinciden con la misma ecuación.)

    1. \(3(x+5)=17\)
    2. \(3x+5=17\)
    3. \(5(x+3)=17\)
    4. \(5x+3=17\)
    1. La maestra de Jada llena una bolsa de viaje con 5 copias de un libro de texto. El peso de la bolsa y libros es de 17 libras. La bolsa de viaje vacía pesa 3 libras. ¿Cuánto pesa cada libro?
    2. Un pedazo de escenario para la obra escolar tiene la forma de un rectángulo de 5 pies de largo. El diseñador decide aumentar la longitud. Habrá 3 rectángulos idénticos con una longitud total de 17 pies. ¿En cuánto aumentó el diseñador la longitud de cada rectángulo?
    3. Elena gasta 17 dólares y compra un libro de $3 y un marcador por cada uno de sus 5 primos. ¿Cuánto cuesta cada marcador?
    4. Noah empaca bolsas en la despensa de alimentos para entregarlas a las familias. Empaca 5 bolsas que pesan un total de 17 libras. Cada bolsa contiene 3 libras de comestibles y un paquete de papeles con información relacionada con la salud. ¿Cuánto pesa cada paquete de papeles?
    5. Andre tiene 3 veces más lápices que Noé y 5 bolígrafos. Tiene 17 bolígrafos y lápices todos juntos. ¿Cuántos lápices tiene Noah?

    Ejercicio\(\PageIndex{7}\)

    Elena caminó 20 minutos más que Lin. Jada caminó el doble de tiempo que Elena. Jada caminó 90 minutos. La ecuación\(2(x+20)=90\) describe esta situación. Coincide cada expresión con la declaración de la historia con la expresión que representa.

    1. \(x\)
    2. \(x+20\)
    3. \(2(x+20)\)
    4. \(90\)
    1. El número de minutos que caminó Jada
    2. El número de minutos que Elena caminó
    3. El número de minutos que Lin caminó

    This page titled 6.1.6: Distinguir entre dos tipos de situaciones is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.