6.2.1: Razonamiento sobre la resolución de ecuaciones (Parte 1)

Lección

Veamos cómo una percha balanceada es como una ecuación y mover su peso es como resolver la ecuación.

Ejercicio\(\PageIndex{1}\): Hanger Diagrams

En los dos diagramas, todos los triángulos pesan igual y todos los cuadrados pesan lo mismo.

Para cada diagrama, venga con.

1. Una cosa que debe ser verdad
2. Una cosa que podría ser verdad
3. Una cosa que no puede ser verdad

Figura\(\PageIndex{1}\): Dos diagramas de colgador. Primera percha, desequilibrada con lado izquierdo inferior, lado izquierdo, triángulo verde, lado derecho, cuadrado azul. Segunda percha, balanceada, lado izquierdo, triángulo verde, lado derecho, tres cuadrados azules, un círculo rojo.

Ejercicio\(\PageIndex{2}\): Hanger and Equation Matching

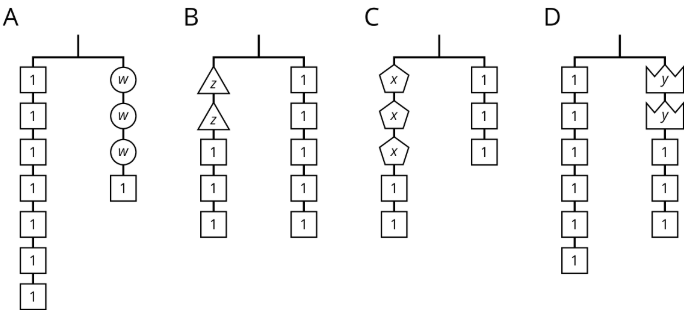
En cada percha balanceada, las figuras con la misma letra tienen el mismo peso.

1. Haga coincidir cada percha con una ecuación. Complete la ecuación escribiendo\(x\),\(y\),\(z\), o\(w\) en la caja vacía.
   • \(2 ?+3=5\)
   • \(3 ?+2=3\)
   • \(6=2?+3\)
   • \(7=3?+1\)
2. Encuentra la solución a cada ecuación. Usa la percha para explicar qué significa la solución.

Figura\(\PageIndex{2}\): Cuatro diagramas de percha balanceados, A, B, C, D. Diagrama A, lado izquierdo, 7 cuadrados, 1, lado derecho, tres círculos, w, 1 cuadrado, 1. Diagrama B, lado izquierdo, 2 triángulos, z, 3 cuadrados, 1, lado derecho, 5 cuadrados, 1. Diagrama C, lado izquierdo, 3 pentágonos, x, 2 cuadrados, 1, lado derecho, 3 cuadrados, 1. Diagrama D, lado izquierdo, 6 cuadrados, lado derecho, 1, 2 coronas, y, 3 cuadrados, 1.

Ejercicio\(\PageIndex{3}\): Use Hangers to Understand Equation Solving

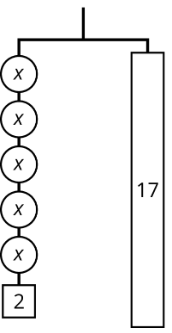
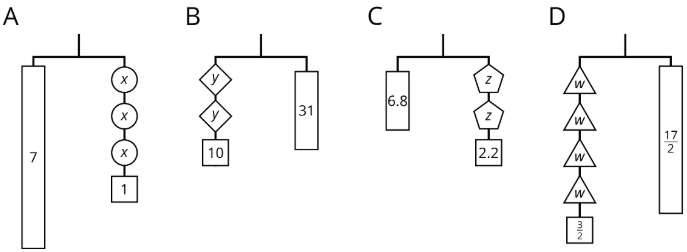
Aquí hay algunas perchas balanceadas donde cada pieza está etiquetada con su peso. Para cada diagrama:

1. Escribe una ecuación.
2. Explica cómo calcular el peso de una pieza etiquetada con una letra razonando sobre el diagrama.
3. Explicar cómo calcular el peso de una pieza etiquetada con una letra razonando sobre la ecuación.

Figura\(\PageIndex{3}\): Cuatro diagramas de colgador balanceados, A, B, C, D. Diagrama A, lado izquierdo, rectángulo, 7, lado derecho, 3 círculos, x, cuadrado, 1. Diagrama B, lado izquierdo, 2 diamantes, y, cuadrado, 10, lado derecho, rectángulo, 31. Diagrama C, lado izquierdo, rectángulo 6.8, lado derecho 2 pentágonos, z, cuadrado 2.2. Diagrama D, lado izquierdo, 4 triángulos, w, cuadrado, 3 sobre 2, lado derecho, rectángulo, 17 sobre 2.

Resumen

En esta lección, trabajamos con dos formas de demostrar que dos cantidades son iguales: una percha balanceada y una ecuación. Podemos usar una percha balanceada para pensar en pasos para encontrar una cantidad desconocida en una ecuación asociada.

El colgador muestra un peso total de 7 unidades en un lado que se equilibra con 3 pesos iguales desconocidos y un peso de 1 unidad en el otro. Una ecuación que representa la relación es\(7=3x+1\).

Figura\(\PageIndex{4}\)

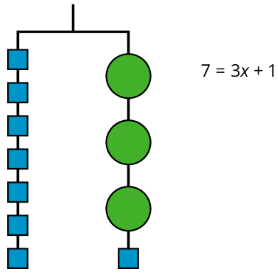
Podemos quitar un peso de 1 unidad de cada lado y la percha se mantendrá equilibrada. Esto es lo mismo que restar 1 de cada lado de la ecuación.

Figura\(\PageIndex{5}\): Percha balanceada, lado izquierdo, 6 cuadrados azules y uno cuadrado rojo siendo removido. Lado derecho, se quitan 3 cuadrados verdes y un cuadrado rojo. Al lado, una ecuación 7 menos 1 = 3 + 1 menos 1, con cada menos 1 escrito en rojo.

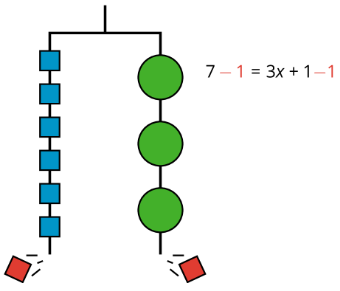
Una ecuación para la nueva percha balanceada es\(6=3x\).

Figura\(\PageIndex{6}\)

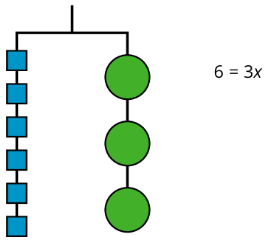
Por lo que la percha se equilibrará con\(\frac{1}{3}\) del peso en cada lado:\(\frac{1}{3}\cdot 6=\frac{1}{3}\cdot 3x\).

Figura\(\PageIndex{7}\): Percha balanceada, lado izquierdo 6 cuadrados azules, lado derecho, tres círculos verdes. Se dibuja una línea punteada alrededor de cada uno de los 3 grupos, cada grupo consta de dos cuadrados azules del lado izquierdo y un círculo verde desde el lado derecho. Al lado, una ecuación dice 6=3x.

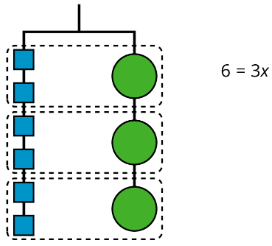
Los dos lados de la percha se equilibran con estos pesos: 6 pesos de 1 unidad en un lado y 3 pesos de tamaño desconocido en el otro lado.

Figura\(\PageIndex{8}\)

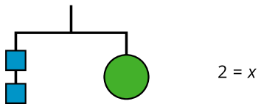
Aquí hay una manera concisa de escribir los pasos anteriores:

\(\begin{array}{lr}{7=3x+1}&{}\\{6=3x}&{\text{after subtracting 1 from each side}}\\{2=x}&{\text{after multiplying each side by }\frac{1}{3}}\end{array}\)

Practica

Ejercicio\(\PageIndex{4}\)

Existe una relación proporcional entre el volumen de una muestra de helio en litros y la masa de esa muestra en gramos. Si la masa de una muestra es de 5 gramos, su volumen es de 28 litros. (5, 28) se muestra en la gráfica a continuación.

Figura\(\PageIndex{9}\)

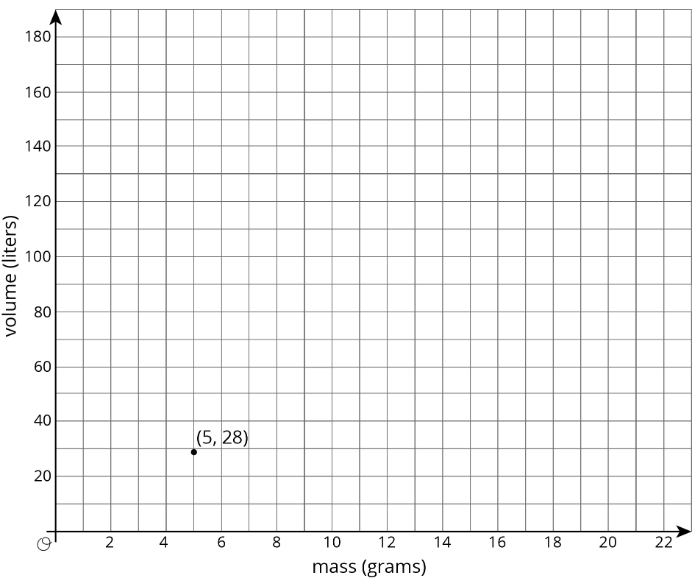
1. ¿Cuál es la constante de proporcionalidad en esta relación?
2. Ante esta situación, ¿cuál es el significado del número que encontraste en la parte a?
3. Agrega al menos tres puntos más a la gráfica anterior, y etiqueta con sus coordenadas.
4. Escribir una ecuación que muestre la relación entre la masa de una muestra de helio y su volumen. Use\(m\) para masa y\(v\) volumen.

(De la Unidad 2.4.2)

Ejercicio\(\PageIndex{5}\)

Explica cómo se comparan las partes de la percha balanceada con las partes de la ecuación.

\(7=2x+3\)

Figura\(\PageIndex{10}\)

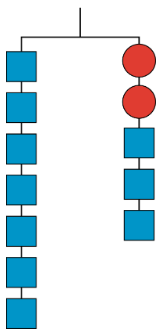
Ejercicio\(\PageIndex{6}\)

Para la percha a continuación:

1. Escribe una ecuación para representar el colgador.
2. Dibuja más perchas para mostrar cada paso que darías para encontrar\(x\). Explica tu razonamiento.
3. Escribe una ecuación para describir cada percha que dibujaste. Describa cómo cada ecuación coincide con su colgador.

Figura\(\PageIndex{11}\)