6.2.2: Razonamiento sobre la Resolución de Ecuaciones (Parte 2)

Lección

Usemos perchas para entender dos formas diferentes de resolver ecuaciones con paréntesis.

Ejercicio\(\PageIndex{1}\): Equivalent to \(2(x+3)\)

Seleccione todas las expresiones equivalentes a\(2(x+3)\).

1. \(2\cdot (x+3)\)
2. \((x+3)2\)
3. \(2\cdot x+2\cdot 3\)
4. \(2\cdot x+3\)
5. \((2\cdot x)+3\)
6. \((2+x)3\)

Ejercicio\(\PageIndex{2}\): Either Or

1. Explique por qué cualquiera de estas ecuaciones podría representar este colgador:

Figura\(\PageIndex{1}\)

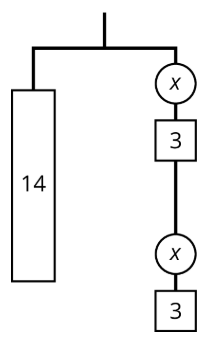
\(14=2(x+3)\)o\(14=2x+6\)

2. Encuentra el peso de un círculo. Esté preparado para explicar su razonamiento.

Ejercicio\(\PageIndex{3}\): Use Hangers to Understand Equation Solving, Again

Aquí hay algunas perchas balanceadas. Cada pieza está etiquetada con su peso.

Figura\(\PageIndex{2}\): Diagrama de cuatro colgadores balanceados. Primer diagrama, lado izquierdo, dos grupos, cada grupo tiene círculo x, cuadrado 5, lado derecho, rectángulo, 16. Segundo diagrama, lado izquierdo, dos grupos, cada grupo tiene triángulo y, cuadrado 200, lado derecho, rectángulo, 3000. Tercer diagrama, lado izquierdo, rectángulo 20 punto 8, lado derecho 4 grupos, cada grupo tiene pentágono z, cuadrado 1 punto 1. Cuarto diagrama, lado izquierdo, rectángulo, 20 sobre 3, lado izquierdo, dos grupos, cada grupo tiene corona w y cuadrado 2 sobre 3.

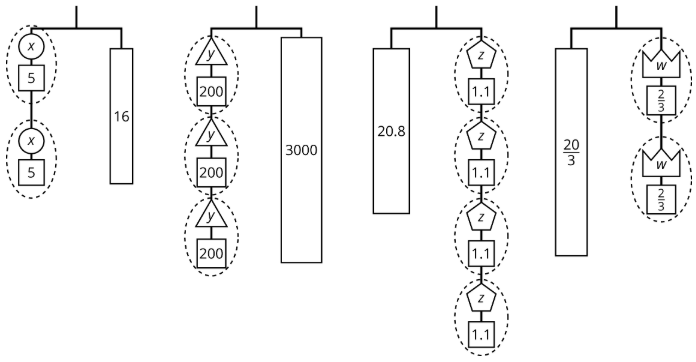
1. Asigne una de estas ecuaciones a cada colgador:
   \[\begin{array}{lll}{2(x+5)=16}&{\qquad}&{3(y+200)=3,000}\\{20.8=4(z+1.1)}&{\qquad}&{\frac{20}{3}=2(w+\frac{2}{3})}\end{array}\nonumber\]
2. Explica cómo calcular el peso de una pieza etiquetada con una letra razonando sobre el diagrama.
3. Explicar cómo calcular el peso de una pieza etiquetada con una letra razonando sobre la ecuación.

Resumen

La percha balanceada muestra 3 pesos iguales desconocidos y 3 pesos de 2 unidades a la izquierda y un peso de 18 unidades a la derecha.

Hay 3 pesos desconocidos más 6 unidades de peso a la izquierda. Podríamos representar esta percha balanceada con una ecuación y resolver la ecuación de la misma manera que lo hicimos antes.

Figura\(\PageIndex{3}\)

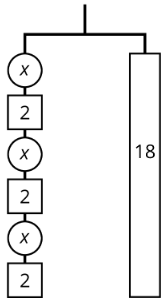
\(\begin{aligned}3x+6&=18 \\ 3x&=12 \\ x&=4\end{aligned}\)

Ya que hay 3 grupos de\(x+2\) a la izquierda, podríamos representar esta percha con una ecuación diferente:\(3(x+2)=18\).

Figura\(\PageIndex{4}\)

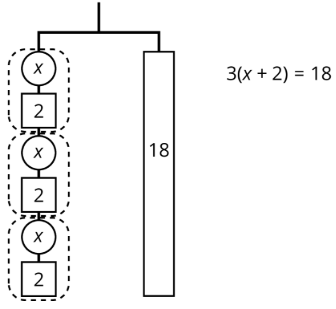
Los dos lados de la percha se equilibran con estos pesos: 3 grupos de\(x+2\) en un lado, y 18, o 3 grupos de 6, en el otro lado.

Figura\(\PageIndex{5}\): Percha balanceada, lado izquierdo, círculo etiquetado x, cuadrado etiquetado 2, círculo etiquetado x, cuadrado etiquetado 2, círculo etiquetado x, cuadrado etiquetado 2, lado derecho, rectángulo no etiquetado. Se dibuja una línea punteada alrededor de tres grupos, cada grupo contiene un círculo y un cuadrado desde el lado izquierdo y un tercio del rectángulo en el lado derecho. Al lado, una ecuación dice 3 (x + 2) = 18.

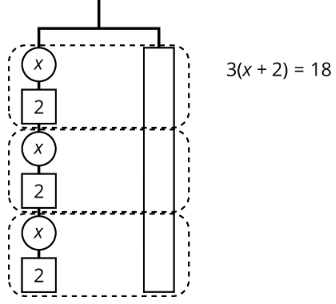
Los dos lados de la percha se equilibrarán con\(\frac{1}{3}\) del peso en cada lado:\(\frac{1}{3}\cdot 3(x+2)=\frac{1}{3}\cdot 18\).

Figura\(\PageIndex{6}\)

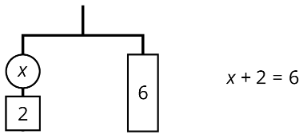
Podemos quitar 2 unidades de peso de cada lado, y la percha se mantendrá equilibrada. Esto es lo mismo que restar 2 de cada lado de la ecuación.

Figura\(\PageIndex{7}\): Percha balanceada. Lado izquierdo, círculo etiquetado x y cuadrado etiquetado 2, el cuadrado parece estar suelto de la percha. Lado derecho, rectángulo etiquetado 4 y cuadrado etiquetado 2, el cuadrado parece estar suelto de la percha. Al lado, y la ecuación dice x + 2 = 4 + 2.

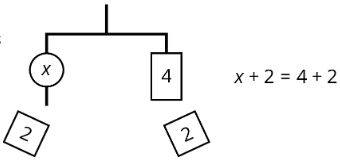
Una ecuación para la nueva percha balanceada es\(x=4\). Esto da la solución a la ecuación original.

Figura\(\PageIndex{8}\)

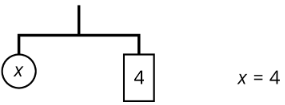
Aquí hay una manera concisa de escribir los pasos anteriores:

\(\begin{array}{lr}{3(x+2)=18}&{}\\{x+2=6}&{\text{after multiplying each side by }\frac{1}{3}}\\{x=4}&{\text{after subtracting }2\text{ from each side}}\end{array}\)

Practica

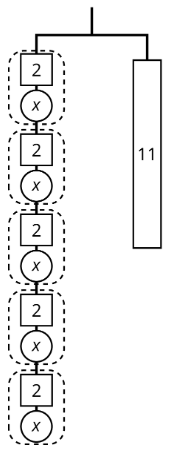
Ejercicio\(\PageIndex{4}\)

Aquí hay una percha:

1. Escribe una ecuación para representar el colgador.
2. Resuelve la ecuación razonando sobre la ecuación o el colgador. Explica tu razonamiento.

Figura\(\PageIndex{9}\)

Ejercicio\(\PageIndex{5}\)

Explique cómo\(9=3(x+2)\) se representa cada parte de la ecuación en el colgador.

Figura\(\PageIndex{10}\)

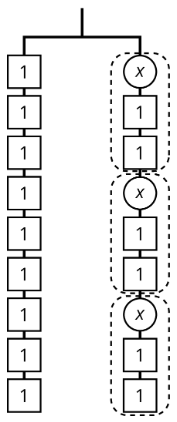
• \(x\)
• \(9\)
• \(3\)
• \(x+2\)
• \(3(x+2)\)
• el signo igual

Ejercicio\(\PageIndex{6}\)

Seleccione la palabra de la siguiente lista que mejor describa cada situación.

1. Depositas dinero en una cuenta de ahorros, y cada año la cantidad de dinero en la cuenta aumenta 2.5%.
2. Por cada auto vendido, a un vendedor de autos se le paga el 6% del precio del auto.
3. Alguien que come en un restaurante paga un 20% extra del precio de la comida. Este dinero extra lo guarda la persona que sirvió la comida.
4. Una tienda de muebles antiguos paga $200 por una silla, agrega el 50% de esa cantidad y vende la silla por $300.
5. El precio normal de un colchón es de $600, pero está a la venta por 10% de descuento.
6. Por cualquier artículo que compres en Texas, pagas un 6.25% adicional del precio del artículo al gobierno del estado.

1. Impuestos
2. Comisión
3. Descuento
4. Marcado
5. Propina o propina
6. Intereses

(De la Unidad 4.3.2)

Ejercicio\(\PageIndex{7}\)

Clare dibujó este diagrama para que coincidiera con la ecuación\(2x+16=50\), pero obtuvo la solución equivocada como resultado de usar este diagrama.

Figura\(\PageIndex{11}\)

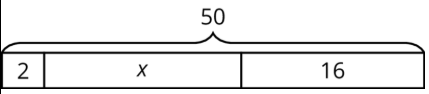
1. ¿Qué valor de se\(x\) puede encontrar usando el diagrama?
2. Muestra cómo arreglar el diagrama de Clare para que coincida correctamente con la ecuación.
3. Utilice el nuevo diagrama para encontrar un valor correcto para\(x\).
4. Explique cómo cometió el error que cometió Clare cuando dibujó su diagrama.

(De la Unidad 6.1.3)