8.1.6: Estimación de probabilidades mediante simulación

Lección

Simulemos situaciones del mundo real.

Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Spinners

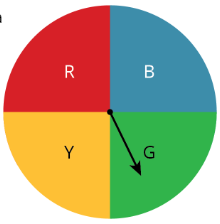
¿Qué spinner no pertenece?

Figura\(\PageIndex{1}\)

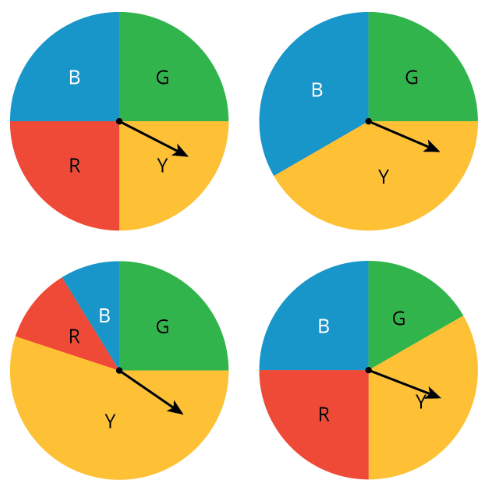
Ejercicio\(\PageIndex{2}\): Deigo's Walk

Tu profesor le dará a tu grupo los suministros para una de las tres simulaciones diferentes. Sigue estas instrucciones para simular 15 días de caminata de Diego. Los primeros 3 días se han hecho por ti.

• Simular un día:
  • Si su grupo recibe una bolsa de papeles, mételo en la bolsa y seleccione un papel sin mirar dentro.
  • Si su grupo recibe un spinner, gírelo y vea dónde se detiene.
  • Si tu grupo obtiene dos cubos numéricos, enrolla ambos cubos y agrega los números que aterrizan boca arriba. Una suma de 2—8 significa que Diego tiene que esperar.
• Registrar en la tabla si Diego tuvo o no que esperar más de 1 minuto.
• Calcular el número total de días y la fracción acumulada de días que Diego ha tenido que esperar hasta el momento.
• En la gráfica, trazar el número de días y la fracción que Diego ha tenido que esperar. Conecta cada punto por una línea.
• Si tu grupo tiene la bolsa de papeles, vuelve a poner el papel en la bolsa y agítalo para mezclar los papeles.
• Pasar los suministros a la siguiente persona del grupo.

Figura\(\PageIndex{2}\): Gráfica de dos segmentos de línea conectados en una cuadrícula de coordenadas con el origen marcado O. El eje horizontal se etiqueta día, con los números del 0 al 24, en incrementos de 2, indicados. Hay líneas verticales de rejilla a medio camino entre ellas. El eje vertical se etiqueta fracción de días Diego tuvo que esperar con los números 0 punto 1 a 1, en incrementos de 0 punto 1, indicado. El primer segmento de línea comienza en el punto con coordenadas 1 coma 0 y se mueve hacia arriba y hacia la derecha, terminando en el punto con coordenadas 2 coma 0 punto 5. El segundo segmento de línea comienza donde termina la primera línea, y se mueve ligeramente hacia arriba y hacia la derecha, terminando en el punto con coordenadas 3 coma 0 punto 6 7.

Mesa\(\PageIndex{1}\)

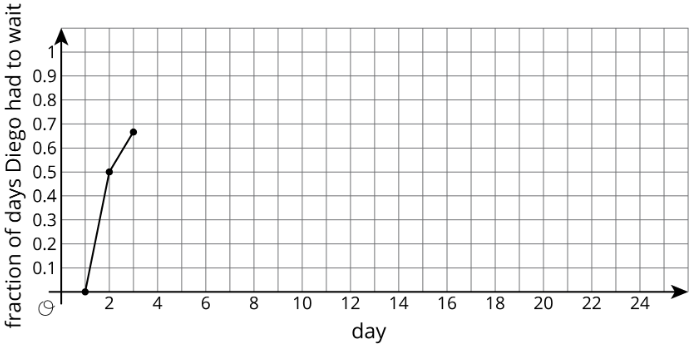
día	¿Diego tiene que esperar más de 1 minuto?	número total de días Diego tuvo que esperar	fracción de días Diego tuvo que esperar
1	no	0	\(\frac{0}{1}=0.00\)
2	si	1	\(\frac{1}{2}=0.50\)
3	si	2	\(\frac{2}{3}\approx 0.67\)
4
5
6
7
8
9
10
11
12
13
14
15

1. Con base en los datos que has recopilado, ¿crees que la fracción de días que Diego tiene que esperar después del día 16 estará más cerca de 0.9 o 0.7? Explica o muestra tu razonamiento.
2. Continuar la simulación por 10 días más. Registre sus resultados en esta tabla y en la gráfica anterior.

   Mesa\(\PageIndex{2}\)

   día	¿Diego tiene que esperar más de 1 minuto?	número total de días Diego tuvo que esperar	fracción de días Diego tuvo que esperar
   16
   17
   18
   19
   20
   21
   22
   23
   24
   25

3. ¿Qué notas de la gráfica?
4. Con base en la gráfica, estime la probabilidad de que Diego tenga que esperar más de 1 minuto para cruzar el paso de peatones.

¿Estás listo para más?

Veamos por qué los valores tienden a no cambiar mucho después de hacer la simulación muchas veces.

1. Después de hacer la simulación 4 veces, un grupo encuentra que Diego tuvo que esperar 3 veces. ¿Cuál es una estimación de la probabilidad que Diego tiene de esperar en base a estos resultados?
   1. Si este grupo hace la simulación 1 vez más, ¿cuáles son los dos posibles resultados para la quinta simulación?
   2. Para cada posibilidad, estime la probabilidad que Diego tiene de esperar.
   3. ¿Cuáles son las diferencias entre las posibles estimaciones después de 5 simulaciones y la estimación después de 4 simulaciones?
2. Después de hacer la simulación 20 veces, este grupo encuentra que Diego tuvo que esperar 15 veces. ¿Cuál es una estimación de la probabilidad que Diego tiene de esperar en base a estos resultados?
   1. Si este grupo hace la simulación 1 vez más, ¿cuáles son los dos posibles resultados para la vigésima primera simulación?
   2. Para cada posibilidad, estime la probabilidad que Diego tiene de esperar.
   3. ¿Cuáles son las diferencias entre las posibles estimaciones después de 21 simulaciones y la estimación después de 20 simulaciones?
3. Utilice estos resultados para explicar por qué un solo resultado después de muchas simulaciones no afecta la estimación tanto como un solo resultado después de solo unas pocas simulaciones.

Ejercicio\(\PageIndex{3}\): Designing Experiments

Para cada situación, describa un experimento casual que lo representaría de manera justa.

1. Seis personas van a salir a almorzar juntas. Uno de ellos será seleccionado al azar para elegir a qué restaurante ir. ¿Quién puede elegir?
2. Después de que un robot se ponga de pie, es igualmente probable que dé un paso adelante con su pie izquierdo o su pie derecho. ¿Qué pie utilizará para su primer paso?
3. En un juego de computadora, hay tres túneles. Cada vez que se carga el nivel, la computadora selecciona aleatoriamente uno de los túneles para que conduzca al castillo. ¿Qué túnel es?
4. Tu escuela está tomando 4 autobuses de estudiantes en un viaje de campo. ¿Te asignarán al mismo autobús en el que está montando tu profesor de matemáticas?

Resumen

A veces es más fácil estimar una probabilidad haciendo una simulación. Una simulación es un experimento que se aproxima a una situación en el mundo real. Las simulaciones son útiles cuando es difícil o requiere mucho tiempo recopilar suficiente información para estimar la probabilidad de algún evento.

Por ejemplo, imagina que Andre tiene que trasladarse de un autobús a otro en el camino a su clase de música. La mayoría de las veces hace el traslado bien, pero a veces el primer autobús llega tarde y pierde el segundo autobús. Podríamos montar una simulación con hojas de papel en una bolsa. Cada papel está marcado con una hora en que el primer autobús llega al punto de traslado. Seleccionamos los resbalones al azar de la bolsa. Después de muchos ensayos, calculamos la fracción de las veces que perdió el autobús para estimar la probabilidad de que pierda el autobús en un día determinado.

Entradas en el glosario

Definición: Experimento de azar

Un experimento casual es algo que puedes hacer una y otra vez, y no sabes lo que sucederá cada vez.

Por ejemplo, cada vez que giras el spinner, podría aterrizar en rojo, amarillo, azul o verde.

Figura\(\PageIndex{3}\)

Definición: Evento

Un evento es un conjunto de uno o más resultados en un experimento casual. Por ejemplo, si rodamos un cubo numérico, hay seis posibles resultados.

Figura\(\PageIndex{4}\)

Ejemplos de eventos son “rodar un número menor que 3", “rodar un número par” o “rodar un 5”.

Definición: Resultado

Un resultado de un experimento casual es una de las cosas que pueden suceder cuando haces el experimento. Por ejemplo, los posibles resultados de lanzar una moneda son las cabezas y las colas.

Definición: Probabilidad

La probabilidad de un evento es un número que dice cuán probable es que suceda. Una probabilidad de 1 significa que el evento siempre sucederá. Una probabilidad de 0 significa que el evento nunca sucederá.

Por ejemplo, la probabilidad de seleccionar un bloque lunar al azar de esta bolsa es\(\frac{4}{5}\).

Figura\(\PageIndex{5}\)

Definición: Aleatorio

Los resultados de un experimento casual son aleatorios si todos tienen la misma probabilidad de suceder.

Definición: Sample Space

El espacio muestral es la lista de todos los resultados posibles para un experimento casual.

Por ejemplo, el espacio de muestra para arrojar dos monedas es:

Mesa\(\PageIndex{3}\)

cabezas-cabezas	cabezas-colas-cabeza
cabeza-colas	colas-colas

Definición: Simulación

Una simulación es un experimento que se utiliza para estimar la probabilidad de un evento del mundo real.

Por ejemplo, supongamos que el pronóstico del tiempo dice que hay un 25% de probabilidad de lluvia. Podemos simular esta situación con un spinner con cuatro secciones iguales. Si el spinner se detiene en rojo, representa lluvia. Si el spinner se detiene en cualquier otro color, no representa lluvia.

Figura\(\PageIndex{6}\): Un hilandero circular dividido en 4 partes iguales. La sección superior izquierda es roja y etiquetada R. La sección superior derecha es azul y etiquetada B. La sección inferior derecha es verde y etiquetada G. La sección inferior izquierda es amarilla y etiquetada Y. El dial giratorio apunta a la sección etiquetada G.

Practica

Ejercicio\(\PageIndex{4}\)

El pronóstico del tiempo dice que hay un 75% de posibilidades de que llueva más tarde hoy.

1. Dibuja un spinner que podrías usar para simular esta probabilidad.
2. Describe otra forma en la que podrías simular esta probabilidad.

Ejercicio\(\PageIndex{5}\)

Un experimento producirá uno de diez resultados diferentes con igual probabilidad para cada uno. ¿Por qué sería una mala elección usar un cubo numérico estándar para simular el experimento?

Ejercicio\(\PageIndex{6}\)

Una heladería ofrece 40 sabores diferentes. Para simular el sabor más comúnmente elegido, podrías escribir el nombre de cada sabor en una hoja de papel y ponerlo en una bolsa. Dibuja de la bolsa 100 veces, y mira qué sabor se elige más. Esta simulación no es una buena manera de averiguar el sabor más comúnmente elegido. Explique por qué.

Ejercicio\(\PageIndex{7}\)

Cada conjunto de tres números representa las longitudes, en unidades, de los lados de un triángulo. ¿Qué conjunto no se puede usar para hacer un triángulo?

1. \(7, 6, 14\)
2. \(4, 4, 4\)
3. \(6, 6, 2\)
4. \(7, 8,13\)

(De la Unidad 7.2.2)

Ejercicio\(\PageIndex{8}\)

Existe una relación proporcional entre un volumen medido en tazas y el mismo volumen medido en cucharadas. 48 cucharadas equivalen a 3 tazas, como se muestra en la gráfica.

Figura\(\PageIndex{7}\): Un punto trazado en el plano de coordenadas con el origen etiquetado O. El eje horizontal se etiqueta volumen en cucharadas y se indican los números 0 a 70, en incrementos de 10. Hay cuatro líneas de cuadrícula uniformemente espaciadas entre cada número indicado. El eje vertical está etiquetado como volumen en copas y se indican los números del 0 al 6. El punto indicado tiene coordenadas 48 coma 3.

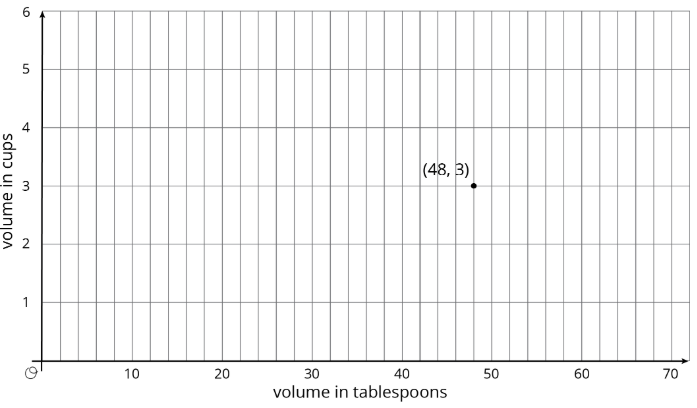
1. Trazar y etiquetar algunos puntos más que representen la relación.
2. Usa una recta para dibujar una línea que represente esta relación proporcional.
3. ¿Para qué valor\(y\) está (\(1,y\)) en la línea que acabas de dibujar?
4. ¿Cuál es la constante de proporcionalidad para esta relación?
5. Escribir una ecuación que represente esta relación. Use\(c\) para tazas y\(t\) para cucharadas.

(De la Unidad 2.5.1)