8.3.3: ¿Qué hace que una buena muestra?

Última actualización
Guardar como PDF

Page ID: 119108

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lección

Veamos qué hace que una buena muestra.

Ejercicio$\PageIndex{1}$: Number Talk: Division by Powers of 10

Encuentra mentalmente el valor de cada cociente.

$34,000\div 10$

$340\div 100$

$34\div 10$

$3.4\div 100$

Ejercicio$\PageIndex{2}$: Selling Paintings

Tu profesor te asignará para trabajar ya sea con medios o medianas.

Un joven artista ha vendido 10 pinturas. Calcula la medida del centro que te asignaron para cada una de estas muestras:
1. Los dos primeros cuadros que vendió fueron por $50 y 350 dólares.
2. En una exhibición de galería, vendió tres pinturas por 250, 400 dólares y 1.200 dólares.
3. Sus pinturas al óleo se han vendido por 410 dólares, 400 y 375 dólares.
Aquí están los precios de venta de sus 10 pinturas:
$$50\quad $200\quad $250\quad $275\quad $280\quad $350\quad $375\quad $400\quad $410\quad $1,200$
Calcula la medida de centro que te asignaron para todos los precios de venta.
Compara tus respuestas con tu pareja. ¿Las medidas de centro para alguna de las muestras fueron cercanas a la misma medida de centro para la población?

Ejercicio$\PageIndex{3}$: Sampling the Fish Market

El precio por libra de bagre en una lonja se registró durante 100 semanas.

Aquí hay parcelas de puntos que muestran la población y tres muestras diferentes de esa población. ¿Qué notas? ¿Qué te preguntas?
Si el objetivo es que la muestra represente a la población, ¿cuál de las muestras funcionaría mejor? ¿Cuál no funcionaría tan bien? Explica tu razonamiento.

Para usar este applet, arrastre la barra gris de abajo hacia arriba para ver las gráficas de puntos de muestra.

¿Estás listo para más?

Al hacer un estudio estadístico, es importante tener en cuenta el objetivo del estudio. Muestras representativas nos dan la mejor información sobre la distribución de la población en su conjunto, ¡pero a veces una muestra representativa no funcionará para el objetivo de un estudio!

Por ejemplo, supongamos que quieres estudiar cómo la discriminación afecta a las personas de tu pueblo. Hacer una encuesta a una muestra representativa de personas en tu pueblo daría información sobre cómo se siente la población en general, pero podría faltar a algunos grupos más pequeños. Describe una forma en la que podrías elegir una muestra de personas para abordar esta pregunta.

Ejercicio$\PageIndex{4}$: Auditing Sales

Una empresa de compras en línea rastrea cuántos artículos venden en diferentes categorías durante cada mes durante un año. Tres auditores diferentes toman muestras de esos datos cada uno. Use las muestras para dibujar parcelas de puntos de cómo podrían ser los datos de población para las categorías de muebles y electrónica.

Muestra de Auditor 1

Figura$\PageIndex{1}$: Una parcela de puntos para ventas mensuales de muebles en línea en cientos. Se indican los números 66 al 74. Los datos titulados Auditor unos muestra son los siguientes: 67 cien, 1 punto. 70 cien, 1 punto. 73 cien, 1 punto.

Muestra de Auditor 2

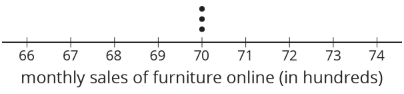
Muestra de Auditor 3

Figura$\PageIndex{3}$: Una parcela de puntos para ventas mensuales de muebles en línea en cientos. Se indican los números 66 al 74. Los datos titulados Auditor threes sample son los siguientes: 71 cien, 2 puntos. 73cientos, 1 punto.

Población

Muestra de Auditor 1

Figura$\PageIndex{5}$: Una gráfica de puntos para las ventas mensuales de electrónica en línea en miles. Se indican los números 38 al 43. Los datos titulados Auditor uno muestra son los siguientes: 39 mil, 1 punto. 41 mil, 1 punto. 43 mil, 1 punto. 43 mil, 1 punto.

Muestra de Auditor 2

Figura$\PageIndex{6}$: Una gráfica de puntos para las ventas mensuales de electrónica en línea en miles. Se indican los números 38 al 43. Los datos titulados Muestra de Auditor dos son los siguientes: 41 mil, 1 punto. 43 mil, 2 puntos.

Muestra de Auditor 3

Figura$\PageIndex{7}$: Una gráfica de puntos para las ventas mensuales de electrónica en línea en miles. Se indican los números 38 al 43. Los datos titulados Muestra del auditor tres son los siguientes: 40 mil, 1 punto. 41 mil, 1 punto. 43 mil, 1 punto. 43 mil, 1 punto.

Población

Resumen

Una muestra representativa de una población tiene una distribución que se asemeja mucho a la distribución de la población en forma, centro y diseminación.

Por ejemplo, considere la distribución de alturas de planta, en cm, para una población de plantas que se muestra en esta parcela de puntos. La media para esta población es de 4.9 cm y el MAD es de 2.6 cm.

Figura$\PageIndex{9}$: Una gráfica de puntos para la altura en centímetros. Se indican los números del 1 al 11. Los datos son los siguientes: 1 centímetro, 5 puntos; 2 centímetros, 7 puntos; 3 centímetros, 8 puntos; 4 centímetros, 8 puntos; 5 centímetros, 5 puntos; 6 centímetros, 3 puntos; 7 centímetros, 2 puntos; 8 centímetros, 2 puntos; 9 centímetros, 1 punto; 10 centímetros, 3 puntos; 11 centímetros, 5 puntos.

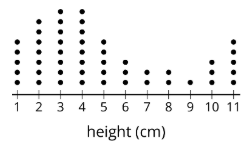
Una muestra representativa de esta población debería tener un pico mayor a la izquierda y uno más pequeño a la derecha, como este. La media para esta muestra es de 4.9 cm y el MAD es de 2.3 cm.

Figura$\PageIndex{10}$: Una gráfica de puntos para la altura en centímetros. Se indican los números del 1 al 11. Los datos son los siguientes: 1 centímetro, 1 punto; 2 centímetros, 2 puntos; 3 centímetros, 4 puntos; 4 centímetros, 4 puntos; 5 centímetros, 2 puntos; 6 centímetros, 1 punto; 7 centímetros, 1 punto; 10 centímetros, 1 punto; 11 centímetros, 2 puntos.

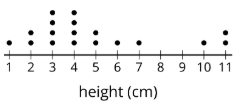
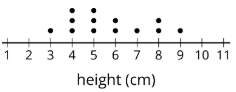
Aquí está la distribución para otra muestra de la misma población. Esta muestra tiene una media de 5.7 cm y una MAD de 1.5 cm. Ambos son muy diferentes de la población, y la distribución tiene una forma muy diferente, por lo que no es una muestra representativa.

Figura$\PageIndex{11}$: Una gráfica de puntos para la altura en centímetros. Se indican los números del 1 al 11. Los datos son los siguientes: 3 centímetros, 1 punto; 4 centímetros, 3 puntos; 5 centímetros, 3 puntos; 6 centímetros, 2 puntos; 7 centímetros, 1 punto; 8 centímetros, 2 puntos; 9 centímetros, 1 punto.

Entradas en el glosario

Definición: Media

La media es una forma de medir el centro de un conjunto de datos. Podemos pensarlo como un punto de equilibrio. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la media es 11.

Para encontrar la media, suma todos los números en el conjunto de datos. Entonces, divídalo por cuántos números hay. $7+9+12+13+14=55$y$55\div 5=11$.

Definición: Desviación Media Absoluta (MAD)

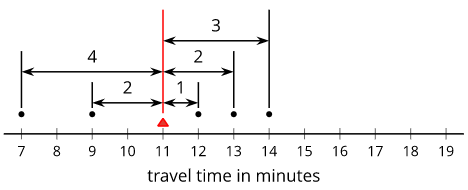
La desviación absoluta media es una forma de medir qué tan extendido está un conjunto de datos. A veces a esto lo llamamos el MAD. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, el MAD es 2.4. Esto nos dice que estos tiempos de viaje suelen estar a 2.4 minutos de distancia de la media, que es 11.

Para encontrar el MAD, sumar la distancia entre cada punto de datos y la media. Entonces, divídalo por cuántos números hay.

$4+2+1+2+3=12$y$12\div 5=2.4$

Definición: Mediana

La mediana es una forma de medir el centro de un conjunto de datos. Es el número medio cuando el conjunto de datos está listado en orden.

Para el conjunto de datos 7, 9, 12, 13, 14, la mediana es 12.

Para el conjunto de datos 3, 5, 6, 8, 11, 12, hay dos números en el medio. La mediana es el promedio de estos dos números. $6+8=14$y$14\div 2=7$.

Definición: Población

Una población es un conjunto de personas o cosas que queremos estudiar.

Por ejemplo, si queremos estudiar las alturas de las personas en diferentes equipos deportivos, la población sería toda la gente de los equipos.

Definición: Representante

Una muestra es representativa de una población si su distribución se asemeja a la distribución de la población en el centro, forma y diseminación.

Por ejemplo, esta gráfica de puntos representa una población.

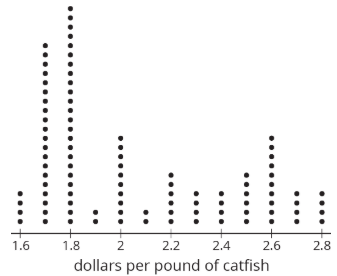
Esta gráfica de puntos muestra una muestra representativa de la población.

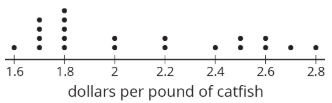
Definición: Muestra

Una muestra es parte de una población. Por ejemplo, una población podría ser todos los estudiantes de séptimo grado en una escuela. Una muestra de esa población son todos los estudiantes de séptimo grado que están en banda.

Práctica

Ejercicio$\PageIndex{5}$

Supongamos que 45% de todos los alumnos de la escuela de Andre trajeron una lata de comida para contribuir a una campaña de comida enlatada. Andre escoge una muestra representativa de 25 alumnos de la escuela y determina el porcentaje de la muestra.

Espera que el porcentaje para esta muestra sea del 45%. ¿Estás de acuerdo? Explica tu razonamiento.

Ejercicio$\PageIndex{6}$

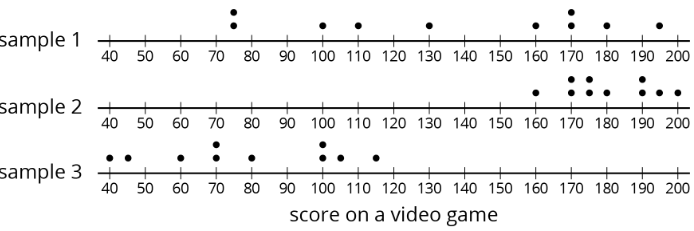
Se trata de una trama de puntos de las partituras en un videojuego para una población de 50 adolescentes.

Figura$\PageIndex{16}$: Gráfica de puntos para partitura en un videojuego. Se indican los números del 40 al 200, en incrementos de 10. Los datos son los siguientes: Puntuación de 40, 1 punto. Puntuación de 45, 1 punto. Puntuación de 60, 1 punto. Puntuación de 65, 2 puntos. Puntuación de 70, 2 puntos. Puntuación de 75, 2 puntos. Puntuación de 80, 2 puntos. Puntuación de 85, 2 puntos. Puntuación de 90, 2 puntos. Puntuación de 95, 2 puntos. Puntuación de 100, 2 puntos. Puntuación de 105, 1 punto. Puntuación de 110, 2 puntos. Puntuación de 115, 2 puntos. Puntuación de 120, 3 puntos. Puntuación de 125, 3 puntos. Puntuación de 130, 5 puntos. Puntuación de 135, 2 puntos. Puntuación de 145, 1 punto. Puntuación de 150, 1 punto. Puntuación de 155, 1 punto. Puntuación de 160, 1 punto. Puntuación de 170, 2 puntos. Puntuación de 175, 2 puntos. Puntuación de 180, 1 punto. Puntuación de 190, 2 puntos. Puntuación de 195, 1 punto. Puntuación de 200, 1 punto.

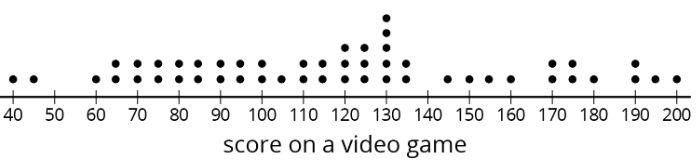
Las tres parcelas de puntos juntas son las puntuaciones de adolescentes en tres muestras de esta población. ¿Cuál de las tres muestras es más representativa de la población? Explique cómo sabe.

Figura$\PageIndex{17}$: Tres parcelas de puntos para la puntuación en un videojuego se etiquetan como muestra 1, muestra 2 y muestra 3. Se indican los números del 40 al 200, en incrementos de 10. Los datos son los siguientes: Muestra 1: Puntuación de 75, 2 puntos. Puntuación de 100, 1 punto. Puntuación de 110, 1 punto. Puntuación de 130, 1 punto. Puntuación de 160, 1 punto. Puntuación de 170, 2 puntos. Puntuación de 180, 1 punto. Puntuación de 195, 1 punto. Muestra 2: Puntuación de 160, 1 punto. Puntuación de 170, 2 puntos. Puntuación de 175, 2 puntos. Puntuación de 180, 1 punto. Puntuación de 190, 2 puntos. Puntuación de 195, 1 punto. Puntuación de 200, 1 punto. Muestra 3: Puntuación de 40, 1 punto. Puntuación de 45, 1 punto. Puntuación de 60, 1 punto. Puntuación de 70, 2 puntos. Puntuación de 80, 1 punto. Puntuación de 100, 2 puntos. Puntuación de 105, 1 punto. Puntuación de 115, 1 punto.

Ejercicio$\PageIndex{7}$

Esta es una gráfica de puntos del número de mensajes de texto enviados un día para una muestra de los estudiantes de una preparatoria local. La muestra estuvo conformada por 30 estudiantes y fue seleccionada para ser representativa de la población.

Figura$\PageIndex{18}$: Gráfica de puntos para el número de mensajes de texto enviados. Se indican los números del 0 al 90, en incrementos de 5. Los datos son los siguientes: 0 mensajes de texto, 6 puntos. 2 mensajes de texto, 2 puntos. 8 mensajes de texto, 3 puntos. 10 mensajes de texto, 2 puntos. 11 mensajes de texto, 1 punto. 13 mensajes de texto, 1 punto. 14 mensajes de texto, 1 punto. 16 mensajes de texto, 1 punto. 17 mensajes de texto, 1 punto. 20 mensajes de texto, 1 punto. 23 mensajes de texto, 1 punto. 24 texto mensajes, 1 punto. 26 mensajes de texto, 1 punto. 30 mensajes de texto, 1 punto. 31 mensajes de texto, 2 puntos. 32 mensajes de texto, 1 punto. 35 mensajes de texto, 1 punto. 41 mensajes de texto, 1 punto. 75 mensajes de texto, 1 punto. 90 mensajes de texto, 1 punto.

¿Qué representan los seis valores de 0 en la gráfica de puntos?
Dado que esta muestra es representativa de la población, describa cómo cree que podría ser una parcela de puntos para toda la población.

Ejercicio$\PageIndex{8}$

Un médico sospecha que podrías tener cierta cepa de gripe y quiere analizar tu sangre para detectar la presencia de marcadores para esta cepa de virus. ¿Por qué sería bueno que el médico tomara una muestra de tu sangre en lugar de usar a la población?

(De la Unidad 8.3.2)

Ejercicio$\PageIndex{9}$

¿Cuántos resultados diferentes hay en cada espacio muestral? Explica tu razonamiento. (No es necesario que escriba las opciones reales, solo proporcione el número y su razonamiento).

A una letra del alfabeto inglés le sigue un dígito del 0 al 9.
La gorra de un equipo de béisbol se selecciona de 3 colores diferentes, 2 cierres diferentes y 4 ubicaciones diferentes para el logotipo del equipo. Se toma la decisión de incluir o no incluir tuberías reflectantes.
Una combinación de casilleros como 7-23-11 utiliza tres números, cada uno del 1 al 40. Los números se pueden usar más de una vez, como 7-23-7.

(De la Unidad 8.2.2)