3.1: Identidades recíprocas y pitagóreas

Los dos tipos más básicos de identidades trigonométricas son las identidades recíprocas y las identidades pitagóricas. Las identidades recíprocas son simplemente definiciones de los recíprocos de las tres relaciones trigonométricas estándar:
\ [\ sec\ theta=\ frac {1} {\ cos\ theta}\ quad\ csc\ theta=\ frac {1} {\ sin\ theta}\ quad\ cot\ theta=\ frac {1} {\ tan\ theta}
\]

También, recuerde las definiciones de las tres relaciones trigonométricas estándar (seno, coseno y tangente):
\ [\ begin {array} {l}
\ sin\ theta=\ frac {o p p} {h y p} {h y p}\\\ cos\ theta=\ frac {a d j} {h y p}
\\\ tan\ theta=\ frac {o p} a d y}
\ fin {matriz}

\]

Si miramos más de cerca las relaciones entre el seno, coseno y tangente, notaremos que\(\frac{\sin \theta}{\cos \theta}=\tan \theta\)
\ [\ frac {\ sin\ theta} {\ cos\ theta} =\ frac {\ left (\ frac {o p p} {h y p}\ right)} {\ left (\ frac {a d j} {h y p}\ right)} =\ frac {o p p} {h y p} *\ frac {h y p} {a d j} =\ frac {o p p} {a d j} =\ tan\ theta
\]

Identidades pitagóricas
Las identidades pitagóricas se basan, por supuesto, en el Teorema de Pitágoras. Si recordamos un diagrama que se introdujo en Capítulo\(2,\) podemos construir estas identidades a partir de las relaciones en el diagrama:

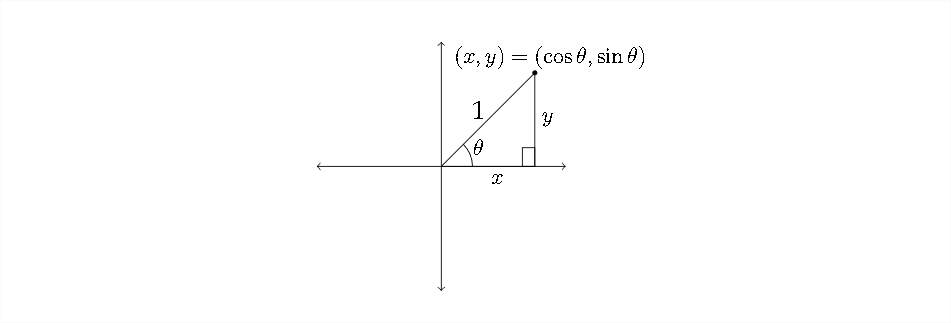
Usando el Teorema de Pitágoras en este diagrama, vemos que\(x^{2}+y^{2}=1^{2},\) así\(x^{2}+y^{2}=1 .\) Pero, también recuerda eso, en el círculo unitario,\(x=\cos \theta\) y\(y=\sin \theta\)

Sustituir esta igualdad nos da la primera Identidad pitagórica:
\ [x^ {2} +y^ {2} =1
\] o
\ [\ cos ^ {2}\ theta+\ sin ^ {2}\ theta=1
\] Esta identidad suele manifestarse en la forma:
\ [\ sin ^ {2}\ theta+\ cos ^ {2}\ theta=1
\]

Si tomamos esta identidad y dividimos en ambos lados por\(\cos ^{2} \theta,\) esto resultará en la primera de dos identidades pitagóricas adicionales:
\ [\ frac {\ sin ^ {2}\ theta} {\ cos ^ {2}\ theta} +\ frac {\ cos ^ {2}\ theta} {\ cos ^ {2}\ theta} =\ frac {1} {\ cos ^ {2}\ theta}
\] o
\ [\ bronceado ^ {2}\ theta+1=\ seg ^ {2}\ theta
\]

Dividir por nos\(\sin ^{2} \theta\) da el segundo:
\ [\ frac {\ sin ^ {2}\ theta} {\ sin ^ {2}\ theta} +\ frac {\ cos ^ {2}\ theta} {\ sin ^ {2}\ theta} =\ frac {1} {\ sin ^ {2}\ theta}
\] o
\ [1+\ cot ^ {2}\ theta^ a=\ csc ^ {2}\ theta
\] Entonces, las tres identidades pitagóricas nos estarán usando son:
\ [\ begin {array} {l}
\ sin ^ {2}\ theta+\ cos ^ {2}\ theta=1\\
\ tan ^ {2}\ theta+1=\ sec ^ {2}\ theta\
1+\ cot ^ {2}\ theta=\ csc ^ {2}\ theta
\ end {array}
\]

Estas identidades pitagóricas a menudo se expresan en otros términos, tales como:
\ [\ begin {array} {l}
\ sin ^ {2}\ theta=1-\ cos ^ {2}\ theta\
\ cos ^ {2}\ theta=1-\ sin ^ {2}\ theta\
\ tan ^ {2}\ theta=\ sec ^ {2}\ theta-1\\
\ cuna ^ {2}\ theta=\ csc ^ {2}\ theta-1
\ end {array}
\]

Al inicio de este capítulo, se discutió la verificación de identidades trigonométricas. Ahora que tenemos algunas identidades básicas con las que trabajar, usémoslas para verificar la igualdad de algunas declaraciones más complicadas. El proceso de verificar identidades trigonométricas implica cambiar un lado de la expresión dada al otro lado. ya que estas no son realmente ecuaciones, no las trataremos de la manera en que tratamos las ecuaciones. Es decir, no vamos a sumar ni restar nada a ambos lados de la declaración (ni multiplicar o dividir por nada de ambos lados tampoco).

Otra razón para no tratar una identidad trigonométrica como una ecuación es que, en la práctica, este proceso generalmente involucra solo un lado de la afirmación. En la resolución de problemas, los matemáticos suelen utilizar identidades trigonométricas para cambiar la apariencia de un problema sin cambiar su valor. En este proceso, una expresión trigonométrica se transforma en otra expresión trigonométrica en lugar de mostrar que dos expresiones trigonométricas son iguales, que es lo que vamos a estar haciendo.

Ejemplo 1
Verificar la identidad\((\sin \theta)(\cot \theta)=\cos \theta\)
Esta es una identidad muy sencilla y puede resolverse utilizando uno de los enfoques fundamentales para trabajar con identidades trigonométricas. Este es el enfoque de escribir todo en términos de senos y cosenos.

Comenzando con la declaración original:
\ [(\ sin\ theta) (\ cot\ theta) =\ cos\ theta
\] Reemplazar\(\cot \theta\) con\(\frac{\cos \theta}{\sin \theta}\)
\ [(\ sin\ theta)\ frac {\ cos\ theta} {\ sin\ theta} =\ cos\ theta
\] Luego cancelando el\(\sin \theta:\)
\ [\ cos\ theta=\ cos \ theta
\]

Existen cuatro enfoques fundamentales para verificar identidades trigonométricas:
1. escribir todo en términos de senos y cosenos
2. hacer un denominador común y sumar fracciones
3. dividir una fracción
4. factor y cancelar
No todos estos pueden ser utilizado en cada problema y algunos problemas usarán combinaciones de estas estrategias. Aquí hay otro ejemplo.

Ejemplo 2
Verifica la identidad\(\tan \theta+\cot \theta=\sec \theta \csc \theta\)
Primero escribiremos todo en términos de senos y cosenos:
\ [\ begin {array} {l}
\ tan\ theta+\ cot\ theta=\ sec\ theta\ csc\ theta\
\ frac {\ sin\ theta} {\ cos\ theta} +\ frac {\ cos\ theta} {\ sin\ theta} =\ frac {1} {\ cos\ theta}\ cdot\ frac {1} {\ sin\ theta}
\ end {array}
\]

A continuación, en el lado izquierdo, podemos sumar las dos fracciones juntas haciendo un denominador común de\(\cos \theta \sin \theta\)
\ begin {alineado}
\ frac {\ sin\ theta} {\ cos\ theta} +\ frac {\ cos\ theta} {\ sin\ theta} &=\ frac {1} {\ cos\ theta}\ cdot\ frac {1} {\ sin\ theta}\
\ frac {\ sin\ theta } {\ sin\ theta}\ cdot\ frac {\ sin\ theta} {\ cos\ theta} +\ frac {\ cos\ theta} {\ sin\ theta}\ cdot\ frac {\ cos\ theta} {\ cos\ theta} &=\ frac {1} {\ cos\ theta}\ cdot\ frac {1} {\ sin\ theta}\\
\ frac {\ sin ^ {2}\ theta} {\ sin\ theta\ cos\ theta} +\ frac {\ cos ^ {2}\ theta} {\ sin\ theta\ cos\ theta} &=\ frac {1} {\ cos \ theta}\ cdot\ frac {1} {\ sin\ theta}\
\ frac {\ sin ^ {2}\ theta+\ cos ^ {2}\ theta} {\ sin\ theta\ cos\ theta} &=\ frac {1} {\ cos\ theta}\ cdot\ frac {1} {\ sin\ theta}\
\ frac {1} {\ sin\ theta\ cos\ theta} &=\ frac {1} {\ sin\ theta\ cos\ theta}
\ end {alineado}

En este ejemplo, se puede ver que primero hemos escrito todo en términos de senos y cosenos, después hemos creado denominadores comunes y sumado las fracciones del lado izquierdo juntas. Una vez hecho esto, podemos sustituir la expresión\(\sin ^{2} \theta+\cos ^{2} \theta\) por\(1,\) ya que esta es la Identidad Pitagórica fundamental.

Ejemplo 3
Verificar la identidad\(\frac{\tan \theta-\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\)
Comenzaremos este problema dividiendo la fracción sobre el denominador. Esto puede ser útil en problemas en los que no hay suma o resta en el denominador. La idea aquí es que desde\(\frac{a}{x}+\frac{b}{x}=\frac{a+b}{x},\) entonces podamos revertir este proceso y decir que\(\frac{a+b}{x}=\frac{a}{x}+\frac{b}{x}\)
En el problema anterior diremos que:

\[\frac{\tan \theta-\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\]\[\frac{\tan \theta}{\sin \theta \cos \theta}-\frac{\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\]\[\frac{\frac{\sin \theta}{\cos \theta}}{\sin \theta \cos \theta}-\frac{\frac{\cos \theta}{\sin \theta}}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\]\[\frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\sin \theta \cos \theta}-\frac{\cos \theta}{\sin \theta} \cdot \frac{1}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\]\[\frac{\cancel{\sin \theta}}{\cos \theta} \cdot \frac{1}{\cancel{\sin \theta} \cos \theta}-\frac{\cancel{\cos \theta}}{\sin \theta} \cdot \frac{1}{\sin \theta \cancel{\cos \theta}}=\sec ^{2} \theta-\csc ^{2} \theta\]\[\frac{1}{\cos ^{2} \theta}-\frac{1}{\sin ^{2} \theta}=\sec ^{2} \theta-\csc ^{2} \theta\]\ [\ seg ^ {2}\ theta-\ csc ^ {2}\ theta=\ seg ^ {2}\ theta-\ csc ^ {2}\ theta
\]

Ejemplo 4
Verificar la identidad\(\frac{\tan ^{2} \theta-\cos ^{2} \theta}{1-\cos ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta\)
En el lado izquierdo, observe la expresión\(1-\cos ^{2} \theta\) en el denominador. Podemos sustituir esto por\(\sin ^{2} \theta,\) lo que es una expresión más sencilla. A menudo es útil tener una expresión más simple en el denominador en lugar de una expresión más complicada.

\ [\ begin {array} {l}
\ frac {\ tan ^ {2}\ theta-\ cos ^ {2}\ theta} {1-\ cos ^ {2}\ theta} =\ seg ^ {2}\ theta-\ cuna ^ {2}\ theta
\ frac {\ tan ^ {2}\ theta-\ cos ^ {2}\ theta}\ sin ^ {2}\ theta} =\ sec ^ {2}\ theta-\ cot ^ {2}\ theta
\ end {array}
\] A continuación, podemos dividir el fracción sobre el denominador de\(\sin ^{2} \theta\)
\ [\ frac {\ tan ^ {2}\ theta-\ cos ^ {2}\ theta} {\ sin ^ {2}\ theta} =\ sec ^ {2}\ theta-\ cot ^ {2}\ theta
\]\ [\ frac {\ tan ^ {2}\ theta} {\ sin ^ {2}\ theta} -\ frac ac {\ cos ^ {2}\ theta} {\ sin ^ {2}\ theta} =\ seg ^ {2}\ theta-\ cuna ^ {2}\ theta
\]

Podemos ver en el lado izquierdo que la expresión\(\frac{\cos ^{2} \theta}{\sin ^{2} \theta}\) es equivalente a\(\cot ^{2} \theta\) pero la primera pieza del lado izquierdo necesita simplificarse un poco más. Reescribiremos\(\tan ^{2} \theta\) como\(\frac{\sin ^{2} \theta}{\cos ^{2} \theta}\) y luego simplificaremos la fracción compleja.
\ [\ begin {array} {c}
\ frac {\ tan ^ {2}\ theta} {\ sin ^ {2}\ theta} -\ frac {\ cos ^ {2}\ theta} {\ sin ^ {2}\ theta} =\ sec ^ {2}\ theta-\ cot ^ {2}\ theta
\\ frac {\ sin ^ {2}\ theta} {\ cos ^ {2}\ theta}} {\ sin ^ {2}\ theta} -\ cuna ^ {2}\ theta=\ sec ^ {2}\ theta-\ cuna ^ {2}\ theta\\

\ frac {\ sin ^ {2}\ theta} {\ cos ^ {2}\ theta}\ cdot\ frac {1} {\ sin ^ {2}\ theta} -\ cuna ^ {2}\ theta=\ sec ^ {2}\ theta-\ cuna ^ {2}\ theta\
\ frac {\ cancel {\ sin ^ {2}\ theta}} {\ cos ^ {2}\ theta}\ cdot\ frac {1} {\ cancel {\ sin ^ {2}\ theta}} -\ cuna ^ {2}\ theta=\ sec ^ {2}\ theta-\ cuna ^ {2} \ theta
\ fin {matriz}
\]

Después de cancelar el ya casi\(\sin ^{2} \theta,\) terminamos:
\ [\ begin {aligned}
\ frac {\ cancel {\ sin ^ {2}\ theta}} {\ cos ^ {2}\ theta}\ cdot\ frac {1} {\ cancel {\ sin ^ {2}\ theta}} -\ cot ^ {2}\ theta &=\ sec ^ {2}\ theta-\ cot ^ {2}\ theta\\
&\ frac {1} {\ cos ^ {2}\ theta} -\ cuna ^ {2} \ theta=\ sec ^ {2}\ theta-\ cot ^ {2}\ theta\\
&\ sec ^ {2}\ theta-\ cot ^ {2}\ theta=\ sec ^ {2}\ theta-\ cot ^ {2}\ theta
\ end {alineado}
\] Las identidades trigonométricas que hemos discutido en esta sección se resumen a continuación:

En los ejemplos anteriores y en los ejercicios, la forma pecado\(\theta\) o\(\cos \theta\) se usa típicamente, sin embargo cualquier letra puede ser utilizada para representar el ángulo en cuestión siempre y cuando sea la MISMA letra en todas las expresiones. Por ejemplo, podemos decir que:
\ [\ sin ^ {2}\ theta+\ cos ^ {2}\ theta=1
\] o podemos decir que

\ [\ sin ^ {2} x+\ cos ^ {2} x=1
\] sin embargo:
\ [\ sin ^ {2}\ theta+\ cos ^ {2} x\ neq 1
\] porque\(\theta\) y\(x\) podrían ser diferentes ángulos!

Ejercicios 3.1
En cada problema verificar la identificación trigonométrica dada.

1. \(\cos \theta(\sec \theta-\cos \theta) = \sin ^{2} \theta\\[4pt] \)

2. \(\tan \theta(\cot \theta+\tan \theta) = \sec ^{2} \theta\\[4pt] \)

3. \(\tan \theta(\csc \theta+\cot \theta)-\sec \theta = 1\\[4pt] \)

4. \(\cot \theta(\sec \theta+\tan \theta)-\csc \theta = 1\\[4pt] \)

5. \(\tan ^{2} \theta \csc ^{2} \theta-\tan ^{2} \theta = 1\\[4pt] \)

6. \( \sin ^{2} \theta \cot ^{2} \theta+\sin ^{2} \theta = 1\\[4pt] \)

7. \(\dfrac{\sin \theta \tan \theta+\sin \theta}{\tan \theta+\tan ^{2} \theta} = \cos \theta\\[4pt] \)

8. \(\dfrac{\cos \theta \cot \theta+\cos \theta}{\cot \theta+\cot ^{2} \theta} = \sin \theta\\[4pt] \)

9. \(\dfrac{(\sin \theta+\cos \theta)^{2}}{\cos \theta}-\sec \theta=2 \sin \theta\\[4pt] \)

10. \( ( \sin \theta+\cos \theta)^{2}+(\sin \theta-\cos \theta)^{2} = 2\\[4pt] \)

11. \(\cos \theta(\tan \theta+\cot \theta) = \csc \theta\\[4pt] \)

12. \(\sin \theta(\cot \theta+\tan \theta) = \sec \theta\\[4pt] \)

13. \(\dfrac{\cos \theta}{\tan \theta}-\csc \theta = -\sin \theta\\[4pt] \)

14. \(\dfrac{\sin \theta}{\cot \theta}-\sec \theta = -\cos \theta\\[4pt] \)

15. \(\dfrac{\csc \theta}{\cos \theta}-\dfrac{\cos \theta}{\csc \theta} = \dfrac{\cot ^{2} \theta+\sin ^{2} \theta}{\cot \theta}\\[4pt] \)

16. \(\dfrac{\sec \theta+\csc \theta}{\tan \theta+\cot \theta} = \sin \theta+\cos \theta\\[4pt] \)

17. \(\dfrac{\sin \theta}{1+\sin \theta}-\dfrac{\sin \theta}{1-\sin \theta} = -2 \tan ^{2} \theta\\[4pt] \)

18. \(\dfrac{\cos \theta}{1+\cos \theta}-\dfrac{\cos \theta}{1-\cos \theta} = -2 \cot ^{2} \theta\\[4pt] \)

19. \(\dfrac{\cot \theta}{1+\csc \theta}-\dfrac{\cot \theta}{1-\csc \theta} = 2 \sec \theta\\[4pt] \)

20. \(\dfrac{\tan \theta}{1+\sec \theta}-\dfrac{\tan \theta}{1-\sec \theta} = 2 \csc \theta\\[4pt] \)

21. \(\dfrac{\sec ^{2} \theta}{1+\cot ^{2} \theta} = \tan ^{2} \theta\\[4pt] \)

22. \(\dfrac{\csc ^{2} \theta}{1+\tan ^{2} \theta} = \cot ^{2} \theta\\[4pt] \)

23. \(\sec ^{4} \theta-\sec ^{2} \theta = \tan ^{4} \theta+\tan ^{2} \theta\\[4pt] \)

24. \(\csc ^{4} \theta-\csc ^{2} \theta = \cot ^{4} \theta+\cot ^{2} \theta\\[4pt] \)

25. \(1-\dfrac{\cos ^{2} \theta}{1+\sin \theta} = \sin \theta\\[4pt] \)

26. \(1-\dfrac{\sin ^{2} \theta}{1+\cos \theta} = \cos \theta\\[4pt] \)

27. \(\dfrac{\sec \theta}{\csc \theta} + \dfrac{\sin \theta}{\cos \theta} = 2 \tan \theta\\[4pt] \)

28. \(\dfrac{1-\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{1-\sin \theta} = 2 \sec \theta\\[4pt] \)

29. \(\dfrac{\cos \theta}{1+\sin \theta}+\dfrac{1+\sin \theta}{\cos \theta} = 2 \sec \theta\\[4pt] \)

30. \(\dfrac{\tan \theta-\cot \theta}{\tan \theta+\cot \theta} = \sin ^{2} \theta-\cos ^{2} \theta\\[4pt] \)

31. \(\dfrac{\sec \theta-\cos \theta}{\sec \theta+\cos \theta} = \dfrac{\sin ^{2} \theta}{1+\cos ^{2} \theta}\\[4pt] \)

32. \(\dfrac{\sec \theta+\tan \theta}{\cot \theta+\cos \theta} = \tan \theta \sec \theta\\[4pt] \)