5.3: Las Otras Funciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 121530

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Objetivos de aprendizaje

Encuentra valores exactos de las funciones trigonométricas secante, cosecante, tangente y cotangente de\(\frac{\pi}{3}\),\(\frac{\pi}{4}\), y\(\frac{\pi}{6}\).
Utilice ángulos de referencia para evaluar las funciones trigonométricas secante, tangente y cotangente.
Utilizar propiedades de funciones trigonométricas pares e impares.
Reconocer y utilizar identidades fundamentales.
Evaluar funciones trigonométricas con una calculadora.

Una rampa para sillas de ruedas que cumpla con los estándares de la Ley de Estadounidenses con Discapacidades debe hacer un ángulo con el suelo cuya tangente sea\(\frac{1}{12}\) o menor, independientemente de su longitud. Una tangente representa una relación, por lo que esto significa que por cada 1 pulgada de subida, la rampa debe tener 12 pulgadas de recorrido. Las funciones trigonométricas nos permiten especificar las formas y proporciones de los objetos independientemente de las dimensiones exactas. Ya hemos definido las funciones seno y coseno de un ángulo. Aunque seno y coseno son las funciones trigonométricas más utilizadas, hay otras cuatro. Juntos conforman el conjunto de seis funciones trigonométricas. En esta sección, investigaremos las funciones restantes.

Encontrar valores exactos de las funciones trigonométricas Secante, Cosecante, Tangente y Cotangente

Para definir las funciones restantes, volveremos a dibujar un círculo unitario con un punto\((x,y)\) correspondiente a un ángulo de\(t\), como se muestra en la Figura\(\PageIndex{1}\). Al igual que con el seno y el coseno, podemos usar las\((x,y)\) coordenadas para encontrar las otras funciones.

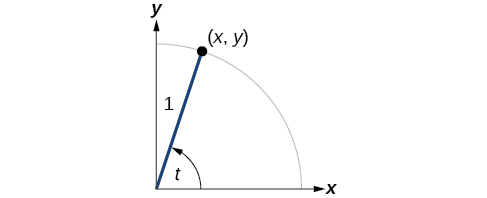
Esta imagen es una gráfica de círculo con ángulo de t inscrito y un radio de 1. El punto de (x, y) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{1}\)

La primera función que definiremos es la tangente. La tangente de un ángulo es la relación entre el valor y y y el valor x del punto correspondiente en el círculo unitario. En la Figura\(\PageIndex{1}\), la tangente de ángulo\(t\) es igual a\(\frac{y}{x},x≠0 \). Debido a que el valor y es igual al seno de\(t\), y el valor x es igual al coseno de\(t\), la tangente del ángulo también se\(t\) puede definir como\( \frac{ \sin t}{ \cos t}, \cos t≠0.\) La función tangente se abrevia como\( \tan.\) Las tres funciones restantes se pueden expresar todas como recíprocos de funciones que ya hemos definido.

La función secante es la recíproca de la función coseno. En la Figura\(\PageIndex{1}\), la secante del ángulo\(t\) es igual a\(\frac{1}{ \cos t} = \frac{1}{x},x≠0\). La función secante se abrevía como\( \sec \).
La función cotangente es el recíproco de la función tangente. En la Figura\(\PageIndex{1}\), la cotangente del ángulo\(t\) es igual a\( \frac{ \cos t}{ \sin t}= \frac{x}{y}, y≠0.\) La función cotangente se abrevia como\( \cot.\)
La función cosecante es la recíproca de la función sinusoidal. En la Figura\(\PageIndex{1}\), el cosecante del ángulo\(t\) es igual a\(\frac{1}{ \sin t}= \frac{1}{y},y≠0.\) La función cosecante se abrevia como\( \csc.\)

FUNCIONES TANGENTE, SECANTE, COSECANTE Y COTANGENTE

Si\(t\) es un número real y\((x,y)\) es un punto donde el lado terminal de un ángulo de\(t\) radianes intercepta el círculo unitario, entonces

\[\begin{align} \tan t &= \frac{y}{x},x≠0 \\ \sec t & =\frac{1}{x},x≠0 \\ \csc t &=\frac{1}{y},y≠0 \\ \cot t &= \frac{x}{y},y≠0 \end{align}\]

Ejemplo\(\PageIndex{1}\): Finding Trigonometric Functions from a Point on the Unit Circle

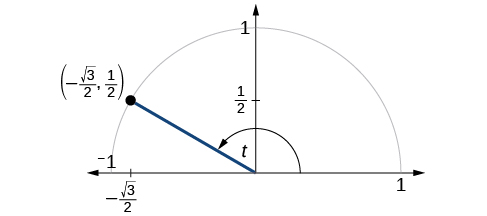
El punto\((−\frac{\sqrt{3}}{2},\frac{1}{2})\) está en el círculo unitario, como se muestra en la Figura\(\PageIndex{2}\). Encontrar\( \sin t, \cos t, \tan t, \sec t, \csc t,\) y\( \cot t\).

Esta es una imagen de una gráfica de círculo con ángulo de t inscrito y con radio 1. El punto de (raíz cuadrada negativa de 3 sobre 2, 1/2) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{2}\)

Solución

Debido a que conocemos las\((x,y)\) coordenadas del punto en el círculo unitario indicado por ángulo\(t\), podemos usar esas coordenadas para encontrar las seis funciones:

\[\begin{align*} \sin t &=y=\dfrac{1}{2} \\ \cos t &=x= −\dfrac{\sqrt{3}}{2} \\ \tan t &= \dfrac{y}{x}= \dfrac{\frac{1}{2}}{−\frac{\sqrt{3}}{2}}=\dfrac{1}{2}(−\dfrac{2}{\sqrt{3}})=−\dfrac{1}{\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \\ \sec t &= \dfrac{1}{x}=\dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2}{\sqrt{3}}=−\dfrac{2\sqrt{3}}{3} \\ \csc t &= \dfrac{1}{y}=\dfrac{1}{\frac{1}{2}}=2 \\ \cot t &= \dfrac{x}{y}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\dfrac{\sqrt{3}}{2}(\dfrac{2}{1})=−\sqrt{3} \end{align*}\]

Ejercicio\(\PageIndex{1}\):

El punto\((\frac{\sqrt{2}}{2},−\frac{\sqrt{2}}{2})\) está en el círculo unitario, como se muestra en la Figura\(\PageIndex{3}\). Encontrar\( \sin t, \cos t, \tan t, \sec t, \csc t,\) y\( \cot t\).

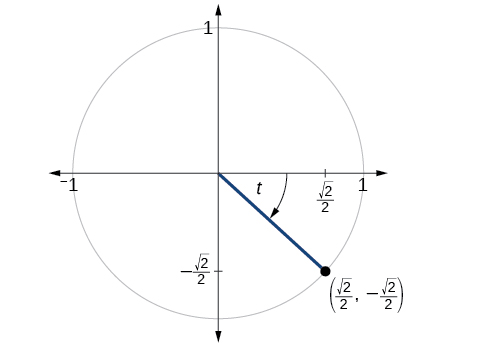
Esta es una imagen de una gráfica de círculo con ángulo de t inscrita con radio 1. El punto de (raíz cuadrada de 2 sobre 2, raíz cuadrada negativa de 2 sobre 2) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{3}\)

Solución

\( \sin t=−\frac{\sqrt{2}}{2}, \cos t= \frac{\sqrt{2}}{2}, \tan t=−1, \sec t=\sqrt{2}, \csc t=−\sqrt{2}, \cot t=−1\)

Ejemplo\(\PageIndex{2}\): Finding the Trigonometric Functions of an Angle

Encontrar\( \sin t, \cos t, \tan t, \sec t, \csc t, \) y\( \cot t\) cuándo\(t=\frac{π}{6}\).

Solución

Anteriormente hemos utilizado las propiedades de los triángulos equiláteros para demostrar que\( \sin \frac{π}{6}=\frac{1}{2}\) y\( \cos \frac{π}{6}=\frac{\sqrt{3}}{2} \). Podemos usar estos valores y las definiciones de tangente, secante, cosecante y cotangente como funciones de seno y coseno para encontrar los valores de función restantes.

\[ \begin{align*} \tan \dfrac{π}{6} & = \dfrac{ \sin \frac{π}{6}}{\cos \frac{π}{6}} \\ & = \dfrac{\frac{1}{2} }{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \\ \sec \dfrac{π}{6} &= \dfrac{1}{ \cos \frac{π}{6}} \\ & = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} \\ \csc \dfrac{π}{6} &= \dfrac{1}{ \sin \frac{π}{6}}= \dfrac{1}{\frac{1}{2}}=2 \\ \cot \dfrac{π}{6} & = \dfrac{ \cos \frac{π}{6}}{ \sin \frac{π}{6}} \\ &= \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} =\sqrt{3} \end{align*}\]

Ejercicio\(\PageIndex{2}\):

Buscar\( \sin t, \cos t, \tan t, \sec t, \csc t,\) y\( \cot t\) cuándo\(t=\frac{π}{3}.\)

Solución

\(\begin{align} \sin \frac{π}{3} & = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} &=\frac{1}{2} \\ \tan \frac{π}{3} &= \sqrt{3} \\ \sec \frac{π}{3} &= 2 \\ \csc \frac{π}{3} &= \frac{2\sqrt{3}}{3} \\ \cot \frac{π}{3} &= \frac{\sqrt{3}}{3} \end{align}\)

Debido a que conocemos los valores de seno y coseno para los ángulos comunes del primer cuadrante, también podemos encontrar los otros valores de función para esos ángulos estableciendo x x igual al coseno e y y igual al seno y luego usando las definiciones de tangente, secante, cosecante y cotangente. Los resultados se muestran en la Tabla\(\PageIndex{1}\).

Mesa\(\PageIndex{1}\)
Ángulo	\(0\)	\(\frac{π}{6}, \text{ or } 30°\)	\(\frac{π}{4}, \text{ or } 45°\)	\(\frac{π}{3},\text{ or }60°\)	\(\frac{π}{2},\text{ or }90°\)
Coseno	\ (0\)” style="vertical-align:middle; ">1	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">\(\frac{1}{2}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">0
Sine	\ (0\)” style="vertical-align:middle; ">0	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">\(\frac{1}{2}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">1
Tangente	\ (0\)” style="vertical-align:middle; ">0	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">1	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">Indefinido
Secante	\ (0\)” style="vertical-align:middle; ">1	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">2	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">Indefinido
Cosecante	\ (0\)” style="vertical-align:middle; ">Indefinido	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">2	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">1
Cotangente	\ (0\)” style="vertical-align:middle; ">Indefinido	\ (\ frac {π} {6},\ text {or} 30°\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="vertical-align:middle; ">1	\ (\ frac {π} {3},\ text {or} 60°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="vertical-align:middle; ">0

Uso de ángulos de referencia para evaluar tangente, secante, cosecante y cotangente

Podemos evaluar funciones trigonométricas de ángulos fuera del primer cuadrante usando ángulos de referencia como ya hemos hecho con las funciones seno y coseno. El procedimiento es el mismo: Encontrar el ángulo de referencia formado por el lado terminal del ángulo dado con el eje horizontal. Los valores de la función trigonométrica para el ángulo original serán los mismos que los del ángulo de referencia, excepto para el signo positivo o negativo, que está determinado por los valores x - e y -en el cuadrante original. La figura\(\PageIndex{4}\) muestra qué funciones son positivas en qué cuadrante.

Para ayudarnos a recordar cuáles de las seis funciones trigonométricas son positivas en cada cuadrante, podemos usar la frase mnemotécnica “A Smart Trig Class”. Cada una de las cuatro palabras de la frase corresponde a uno de los cuatro cuadrantes, comenzando por el cuadrante I y girando en sentido antihorario. En el cuadrante I, que es “A”, una ll de las seis funciones trigonométricas son positivas. En el cuadrante II, “S mart”, sólo s ine y su función recíproca, cosecante, son positivos. En el cuadrante III, “T rig”, solo t angente y su función recíproca, cotangente, son positivos. Finalmente, en el cuadrante IV, “C lass”, solo c osina y su función recíproca, secante, son positivos.

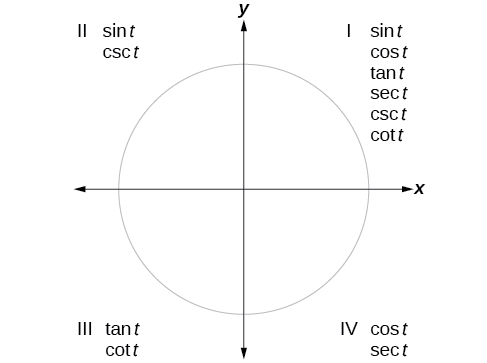
Esta imagen es una gráfica de círculo con cada cuadrante etiquetado. Debajo del cuadrante I, etiquetas para sin t, cos t, tan t, sec t, csc t y cot t. Bajo cuadrante II, etiquetas para sin t y csc t. Bajo cuadrante III, etiquetas para tan t y cot t. Bajo cuadrante IV, etiquetas para cos t, sec t. — Figura\(\PageIndex{4}\)

CÓMO: Dado un ángulo que no está en el primer cuadrante, use ángulos de referencia para encontrar las seis funciones trigonométricas

Mida el ángulo formado por el lado terminal del ángulo dado y el eje horizontal. Este es el ángulo de referencia.
Evaluar la función en el ángulo de referencia.
Observe el cuadrante donde se encuentra el lado terminal del ángulo original. Con base en el cuadrante, determinar si la salida es positiva o negativa.

Ejemplo\(\PageIndex{3}\): Using Reference Angles to Find Trigonometric Functions

Utilice ángulos de referencia para encontrar las seis funciones trigonométricas de\(−\frac{5π}{6}\).

Solución

El ángulo entre el lado terminal de este ángulo y el eje x es\(\frac{π}{6}\), así que ese es el ángulo de referencia. Ya que\(−\frac{5π}{6}\) está en el tercer cuadrante, donde ambos\(x\) y\(y\) son negativos, coseno, seno, secante y cosecante serán negativos, mientras que tangente y cotangente serán positivos.

\[ \begin{align} \cos (−\dfrac{5π}{6}) &=−\dfrac{\sqrt{3}}{2}, \sin (−\dfrac{5π}{6})=−\dfrac{1}{2}, \tan (−\dfrac{5π}{6}) = \dfrac{\sqrt{3}}{3} \\ \sec (−\dfrac{5π}{6}) &=−\dfrac{2\sqrt{3}}{3}, \csc (−\dfrac{5π}{6})=−2, \cot (−\dfrac{5π}{6})=\sqrt{3} \end{align} \]

Ejercicio\(\PageIndex{3}\)

Utilice ángulos de referencia para encontrar las seis funciones trigonométricas de\(−\frac{7π}{4}\).

Solución

\( \sin (−\frac{7π}{4})= \frac{\sqrt{2}}{2}, \cos(\frac{−7π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{−7π}{4})=1,\)

\( \sec (\frac{−7π}{4})= \sqrt{2}, \csc (\frac{−7π}{4})= \sqrt{2}, \cot (\frac{−7π}{4})=1 \)

Uso de funciones trigonométricas pares e impares

Para poder usar nuestras seis funciones trigonométricas libremente con entradas de ángulo positivo y negativo, debemos examinar cómo cada función trata una entrada negativa. Resulta que existe una diferencia importante entre las funciones al respecto.

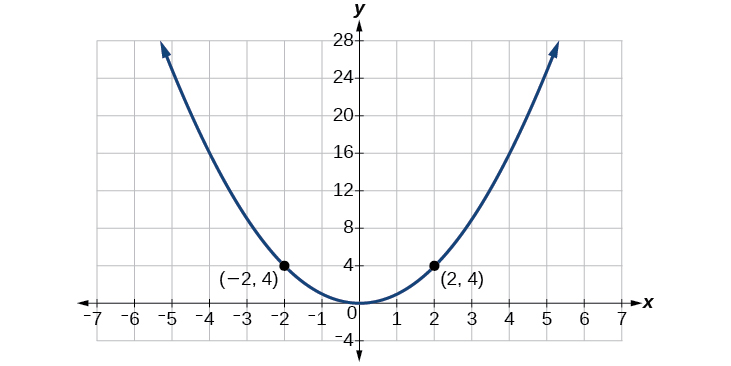
Considera la función\(f(x)=x^2\), que se muestra en la Figura\(\PageIndex{5}\). La gráfica de la función es simétrica alrededor del eje y. A lo largo de la curva, dos puntos cualesquiera con valores x opuestos tienen el mismo valor de función. Esto coincide con el resultado del cálculo:\((4)^2=(−4)^2,(−5)^2=(5)^2\), y así sucesivamente. Así\(f(x)=x^2\) es una función par, una función tal que dos entradas que son opuestas tienen la misma salida. Eso quiere decir\(f(−x)=f(x)\).

Esta es una imagen de una gráfica de parábola orientada hacia arriba y con puntos (-2, 4) y (2, 4) etiquetados. — Figura\(\PageIndex{5}\): La función\(f(x)=x^2\) es una función par.

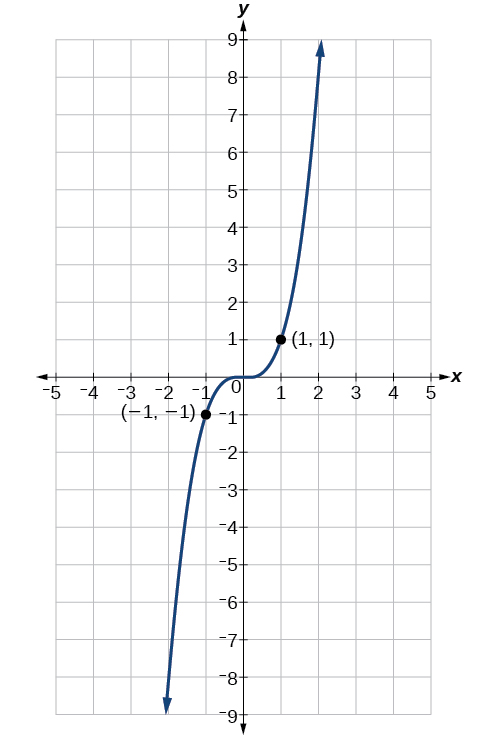
Ahora considere la función\(f(x)=x^3\), que se muestra en la Figura\(\PageIndex{6}\). La gráfica no es simétrica alrededor del eje y. A lo largo de la gráfica, dos puntos cualesquiera con valores x opuestos también tienen valores y opuestos. Así\(f(x)=x^3\) es una función impar, una tal que dos entradas que son opuestas tienen salidas que también son opuestas. Eso quiere decir\(f(−x)=−f(x)\).

Esta es una imagen de una gráfica de la función f de x = x a la tercera potencia con etiquetas para puntos (-1, -1) y (1, 1). — Figura\(\PageIndex{6}\): La función\(f(x)=x^3\) es una función impar.

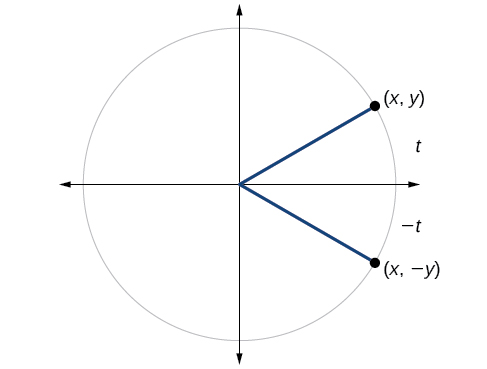
Podemos probar si una función trigonométrica es par o impar dibujando un círculo unitario con un ángulo positivo y otro negativo, como en la Figura\(\PageIndex{7}\). El seno del ángulo positivo es\(y\). El seno del ángulo negativo es − y. La función sinusoidal, entonces, es una función impar. Podemos probar cada una de las seis funciones trigonométricas de esta manera. Los resultados se muestran en la Tabla\(\PageIndex{2}\).

Gráfica de círculo con ángulo de t y -t inscritas. El punto de (x, y) está en la intersección del lado terminal del ángulo t y el borde del círculo. El punto de (x, -y) está en la intersección del lado terminal del ángulo -t y el borde del círculo. — Figura\(\PageIndex{7}\)

Mesa\(\PageIndex{2}\)
\(\begin{align} \sin t &=y \\ \sin (−t) &=−y \\ \sin t &≠sin(−t) \end{align}\)	\( \begin{align} \cos t &=x \\ \cos (−t)=x \\ \cos t &= \cos (−t) \end{align}\)	\(\begin{align} \tan (t) &= \frac{y}{x} \\ \tan (−t) &=−\frac{y}{x} \\ \tan t &≠ \tan (−t) \end{align}\)
\(\begin{align} \sec t &= \frac{1}{x} \\ \sec (−t) &= \frac{1}{x} \\ \sec t &= \sec (−t) \end{align}\)	\( \begin{align} \csc t &= \frac{1}{y} \\ \csc (−t) &= \frac{1}{−y} \\ \csc t &≠ \csc (−t) \end{align}\)	\( \begin{align} \cot t &= \frac{x}{y} \\ \cot (−t) &= \frac{x}{−y} \\ \cot t & ≠ \cot (−t) \end{align}\)

FUNCIONES TRIGONOMÉTRICAS PARES

Una función par es aquella en la que\(f(−x)=f(x)\).
Una función impar es aquella en la que\(f(−x)=−f(x)\).

Coseno y secante son parejos:

\[ \begin{align} \cos (−t) &= \cos t \\ \sec (−t) &= \sec t \end{align}\]

Seno, tangente, cosecante y cotangente son impares:

\[\begin{align} \sin (−t) &=− \sin t \\ \tan (−t) &=−\tan t \\ \csc (−t) &=−\csc t \\ \cot (−t) &=−\cot t \end{align}\]

Ejemplo\(\PageIndex{4}\): Using Even and Odd Properties of Trigonometric Functions

Si la secante del ángulo t es 2, ¿de qué es la secante\(−t\)?

Solución

Secante es una función parejo. La secante de un ángulo es la misma que la secante de su opuesto. Entonces, si la secante del ángulo t es 2, la secante de también\(−t\) es 2.

Ejercicio\(\PageIndex{4}\):

Si la cotangente del ángulo\(t\) es\(\sqrt{3}\), ¿cuál es la cotangente de\(−t?\)

Solución

\(−\sqrt{3}\)

Reconocimiento y Uso de Identidades Fundamentales

Hemos explorado una serie de propiedades de las funciones trigonométricas. Ahora, podemos llevar las relaciones un paso más allá, y derivar algunas identidades fundamentales. Las identidades son declaraciones que son verdaderas para todos los valores de la entrada en la que se definen. Por lo general, las identidades pueden derivarse de definiciones y relaciones que ya conocemos. Por ejemplo, la Identidad Pitagórica que aprendimos anteriormente se derivó del Teorema de Pitágoras y de las definiciones de seno y coseno.

Identidades fundamentales

Podemos derivar algunas identidades útiles a partir de las seis funciones trigonométricas. Las otras cuatro funciones trigonométricas se pueden relacionar de nuevo con las funciones seno y coseno utilizando estas relaciones básicas:

\[ \tan t= \dfrac{ \sin t}{ \cos t} \]

\[ \sec t= \dfrac{1}{\cos t}\]

\[ \csc t= \dfrac{1}{\sin t}\]

\[ \cot t= \dfrac{1}{ \tan t}= \dfrac{ \cos t}{ \sin t} \]

Ejemplo\(\PageIndex{5}\): Using Identities to Evaluate Trigonometric Functions

Dado\( \sin (45°)= \frac{\sqrt{2}}{2}, \cos (45°)= \frac{\sqrt{2}}{2}\), evaluar\( \tan(45°).\)
Dado\( \sin (\frac{5π}{6})= \frac{1}{2}, \cos( \frac{5π}{6})=−\frac{\sqrt{3}}{2},\) evaluar\(\sec (\frac{5π}{6})\).

Solución

Debido a que conocemos los valores de seno y coseno para estos ángulos, podemos usar identidades para evaluar las otras funciones.

\[ \begin{align*} \tan(45°) &=\dfrac{ \sin(45°)}{ \cos (45°)} \\ &= \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \\ & =1 \end{align*} \]
\[\begin{align*} \sec (\dfrac{5π}{6}) &= \dfrac{1}{ \cos (\frac{5π}{6})} \\ &= \dfrac{1}{−\frac{\sqrt{3}}{2}} \\ &= \dfrac{−2\sqrt{3}}{1} \\ &=\dfrac{−2}{\sqrt{3}} \\ &=−\dfrac{2\sqrt{3}}{3} \end{align*}\]

Ejercicio\(\PageIndex{5}\)

Evaluar\(\csc (\frac{7π}{6}).\)

Solución

\(−2\)

Ejemplo\(\PageIndex{6}\): Using Identities to Simplify Trigonometric Expressions

Simplificar\(\frac{ \sec t}{ \tan t}.\)

Solución

Podemos simplificar esto reescribiendo ambas funciones en términos de seno y coseno.

\[\begin{array}{lll} \dfrac{\sec t}{\tan t} & =\dfrac{1 / \cos t}{ \sin t / \cos t} & \text{To divide the functions, we multiply by the reciprocal.} \\ \text{} &= \dfrac{1}{\cos t} \dfrac{ \cos t}{\sin t} & \text{Divide out the cosines.} \\ \text{} & =\dfrac{1}{\sin t} & \text{Simplify and use the identity.} \\ \text{} & = \csc t \end{array}\]

Al demostrar que se\(\frac{ \sec t}{ \tan t}\) puede simplificar para\( \csc t\), de hecho, hemos establecido una nueva identidad.

\[ \dfrac{ \sec t}{ \tan t}= \csc t \nonumber \]

Ejercicio\(\PageIndex{6}\)

Simplificar\(( \tan t)( \cos t).\)

Solución

\( \sin t \)

Formas Alternos de la Identidad Pitagórica

Podemos utilizar estas identidades fundamentales para derivar formas alternativas de la Identidad Pitagórica,\( \cos ^2 t+ \sin ^2 t=1\). Una forma se obtiene dividiendo ambos lados por\( \cos ^2 t:\)

\[ \begin{align} \dfrac{ \cos ^2 t}{ \cos ^2 t} + \dfrac{ \sin ^2 t}{ \cos ^2 t} & = \dfrac{1}{ \cos ^2 t} \\ 1+ \tan ^2 t & = \sec ^2 t \end{align}\]

La otra forma se obtiene dividiendo ambos lados por\( \sin ^2 t\):

\[ \begin{align} \dfrac{ \cos ^2 t}{ \sin ^2 t}+ \dfrac{ \sin ^2 t}{ \sin ^2 t} &= \dfrac{1}{ \sin ^2 t} \\ \cot ^2 t+1 &= \csc ^2 t \end{align}\]

FORMAS ALTERNOS DE LA IDENTIDAD PITAGORANA

\[1+ \tan ^2 t= \sec ^2 t \]

\[ \cot ^2 t+1= \csc ^2 t\]

Ejemplo\(\PageIndex{7}\): Using Identities to Relate Trigonometric Functions

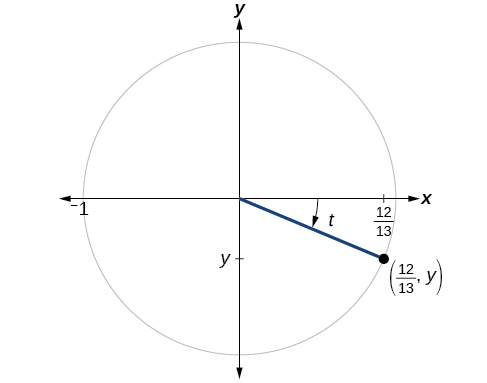
Si cos (t) =1213 cos (t) =1213 y t t está en el cuadrante IV, como se muestra en la Figura\(\PageIndex{8}\), encuentre los valores de las otras cinco funciones trigonométricas.

Esta es una imagen de gráfica de círculo con ángulo de t inscrito. El punto de (12/13, y) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{8}\)

Solución

Podemos encontrar el seno usando la Identidad Pitagórica\( \cos ^2 t+ \sin ^2t=1 \), y las funciones restantes relacionándolas con seno y coseno.

\[ \begin{align} (\dfrac{12}{13})^2+ \sin ^2 t &= 1 \\ \sin ^2 t &=1−(\dfrac{12}{13})^2 \\ \sin ^2 t &=1− \dfrac{144}{169} \\ \sin ^2 t &= \dfrac{25}{169} \\ \sin t &=±\sqrt{\dfrac{25}{169}} \\ \sin t &=±\dfrac{\sqrt{25}}{\sqrt{169}} \\ \sin t &=± \dfrac{5}{13} \end{align} \]

El signo del seno depende de los valores y en el cuadrante donde se ubica el ángulo. Dado que el ángulo está en el cuadrante IV, donde los valores y son negativos, su seno es negativo,\(−\frac{5}{13}\).

Las funciones restantes se pueden calcular usando identidades que las relacionan con seno y coseno.

\[ \begin{align} \tan t &= \dfrac{\sin t}{ \cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}}=−\dfrac{5}{12} \\ \sec t &= \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{12} \\ \csc t &= \dfrac{1}{\sin t}=\dfrac{1}{−\frac{5}{13}} =−\dfrac{13}{5} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{−\frac{5}{12}}=−\dfrac{12}{5} \end{align} \]

Ejercicio\(\PageIndex{7}\):

Si\( \sec (t)=− \frac{17}{8}\) y\(0<t<π,\) encuentra los valores de las otras cinco funciones.

Solución

\( \cos t=−\frac{8}{17}, \sin t=\frac{15}{17}, \tan t=−\frac{15}{8}\)

\( \csc t= \frac{17}{15}, \cot t=−\frac{8}{15} \)

Como comentamos en la apertura del capítulo, una función que repite sus valores en intervalos regulares se conoce como función periódica. Las funciones trigonométricas son periódicas. Para las cuatro funciones trigonométricas, seno, coseno, cosecante y secante, una revolución de un círculo, o\(2π\), dará como resultado las mismas salidas para estas funciones. Y para tangente y cotangente, sólo media revolución dará como resultado las mismas salidas.

Otras funciones también pueden ser periódicas. Por ejemplo, las duraciones de los meses se repiten cada cuatro años. Si x x representa el tiempo de duración, medido en años, y\(f(x)\) representa el número de días en febrero, entonces\(f(x+4)=f(x)\). Este patrón se repite una y otra vez a través del tiempo. Es decir, cada cuatro años, se garantiza que febrero tendrá el mismo número de días que 4 años antes. El número positivo 4 es el número positivo más pequeño que satisface esta condición y se llama el periodo. Un periodo es el intervalo más corto durante el cual una función completa un ciclo completo; en este ejemplo, el periodo es 4 y representa el tiempo que nos lleva estar seguros de que febrero tiene el mismo número de días.

Período de una función

El periodo\(P\) de una función repetitiva f f es el número que representa el intervalo tal que\(f(x+P)=f(x)\) para cualquier valor de\(x\).

El periodo de las funciones coseno, seno, secante y cosecante es\(2π\).

El periodo de las funciones tangente y cotangente es\(π\).

Ejemplo\(\PageIndex{8}\): Finding the Values of Trigonometric Functions

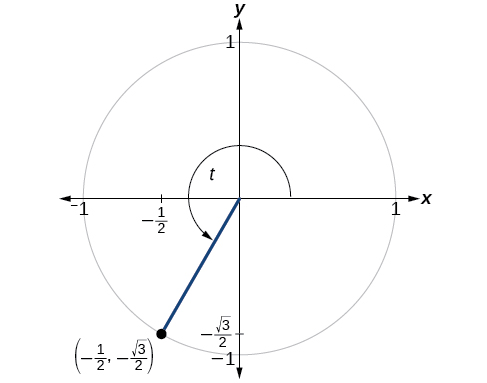
Encuentra los valores de las seis funciones trigonométricas de ángulo con\(t\) base en la Figura\(\PageIndex{9}\).

Esta es una imagen de una gráfica de círculo con ángulo de t inscrito. El punto de (1/2, raíz cuadrada negativa de 3 sobre 2) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{9}\)

Solución

\[\begin{align*} \sin t &= y=−\dfrac{\sqrt{3}}{2} \\ \cos t &=x =−\dfrac{1}{2} \\ \tan t &= \dfrac{ \sin t}{ \cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{−\frac{1}{2}}= \sqrt{3} \\ \sec t &= \dfrac{1}{\cos t} = \dfrac{1}{−\frac{1}{2}}=−2 \\ \csc t &= \dfrac{1}{\sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2\sqrt{3}}{3} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Ejercicio\(\PageIndex{8}\)

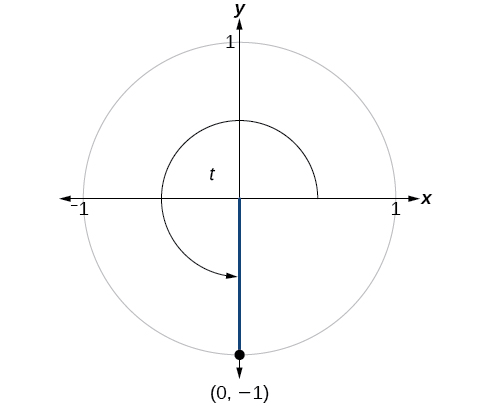
Encuentra los valores de las seis funciones trigonométricas de ángulo con\(t\) base en la Figura\(\PageIndex{10}\).

Esta es una imagen de una gráfica de círculo con ángulo de t inscrito. El punto de (0, -1) está en la intersección del lado terminal del ángulo y el borde del círculo. — Figura\(\PageIndex{10}\)

Solución

\(\begin{align} \sin t &=−1, \cos t=0, \tan t= \text{Undefined} \\ \\sec t &= \text{Undefined}, \csc t=−1, \cot t=0 \end{align}\)

Ejemplo\(\PageIndex{9}\): Finding the Value of Trigonometric Functions

Si\( \sin(t)=−\frac{\sqrt{3}}{2}\) y\( \cos (t)=\frac{1}{2}\), encontrar\( \sec (t),\csc (t),\tan (t), \cot (t).\)

Solución

\[ \begin{align} \sec t &= \dfrac{1}{ \cos t}= \dfrac{1}{\frac{1}{2}}=2 \\ \csc t &= \dfrac{1}{ \sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}−\dfrac{2\sqrt{3}}{3} \\ \tan t &= \dfrac{\sin t}{\cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\sqrt{3} \\ \cot t &= \dfrac{1}{ \tan t}= \dfrac{1}{−\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \end{align}\]

Ejercicio\(\PageIndex{9}\):

Si\(\sin (t)= \frac{\sqrt{2}}{2}\) y\(\cos (t)=\frac{\sqrt{2}}{2},\) encontrar\( \sec (t), \csc (t),\tan (t),\) y\( \cot (t)\).

Solución

\( \sec t= \sqrt{2},\csc t=\sqrt{2}, \tan t=1, \cot t=1\)

Evaluación de funciones trigonométricas con una calculadora

Hemos aprendido a evaluar las seis funciones trigonométricas para los ángulos comunes del primer cuadrante y a utilizarlas como ángulos de referencia para ángulos en otros cuadrantes. Para evaluar las funciones trigonométricas de otros ángulos, utilizamos una calculadora científica o gráfica o un software de computadora. Si la calculadora tiene un modo grado y un modo radianes, confirme que se elija el modo correcto antes de realizar un cálculo.

Evaluar una función tangente con una calculadora científica a diferencia de una calculadora gráfica o sistema de álgebra por computadora es como evaluar un seno o coseno: Ingrese el valor y presione la tecla TAN. Para las funciones recíprocas, puede que no haya claves dedicadas que digan CSC, SEC o COT. En ese caso, la función debe evaluarse como el recíproco de un seno, coseno o tangente.

Si necesitamos trabajar con grados y nuestra calculadora o software no tiene un modo grado, podemos ingresar los grados multiplicados por el factor de conversión\(\frac{π}{180}\) para convertir los grados a radianes. Para encontrar a la secante de\( 30°\), podríamos presionar

\[\mathrm{(for \; a \; scientific \; calculator):\dfrac{1}{30×\frac{π}{180}}COS }\]

\[ \mathrm{(for \; a \; graphing \; calculator): \dfrac{1}{cos(\frac{30π}{180})} }\]

cómo: Dada una medida de ángulo en radianes, utilizar una calculadora científica para encontrar el cosecante

Si la calculadora tiene modo grado y modo radián, configúrela en modo radián.
Ingresa:\(1 \; / \)
Introduzca el valor del ángulo entre paréntesis.
Presione la tecla SIN.
Presiona la tecla =.

cómo: Dada una medida de ángulo en radianes, use una utilidad/calculadora de gráficos para encontrar el cosecante

Si la utilidad gráfica tiene modo grado y modo radián, configúrelo en modo radián.
Ingresa:\(1 \; /\)
Presione la tecla SIN.
Introduzca el valor del ángulo entre paréntesis.
Presione la tecla ENTER.

Ejemplo\(\PageIndex{10}\): Evaluating the Cosecant Using Technology

Evaluar el cosecante de\(\frac{5π}{7}\).

Solución

Para una calculadora científica, ingrese la información de la siguiente manera:

\[ \mathrm{1 / ( 5 × π / 7 ) SIN =}\]

\[ \mathrm{ \csc (\dfrac{5π}{7})≈1.279} \]

Ejercicio\(\PageIndex{10}\):

Evaluar la cotangente de\(−\frac{π}{8}\).

\(≈−2.414\)

medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con otras funciones trigonométricas.

Ecuaciones Clave

Función tangente	\( \tan t= \frac{ \sin t}{\cos t}\)
Función secante	\( \sec t= \frac{1}{ \cos t}\)
Función cosecante	\( \csc t= \frac{1}{ \sin t}\)
Función cotangente	\( \cot t= \frac{1}{\tan t}= \frac{\cos t}{ \sin t}\)

Conceptos clave

La tangente de un ángulo es la relación entre el valor y y y el valor x del punto correspondiente en el círculo unitario.
El secante, el cotangente y el cosecante son todos recíprocos de otras funciones. El secante es el recíproco de la función coseno, la cotangente es el recíproco de la función tangente, y el cosecante es el recíproco de la función sinusoidal.
Las seis funciones trigonométricas se pueden encontrar a partir de un punto en el círculo unitario. Ver Ejemplo.
Las funciones trigonométricas también se pueden encontrar desde un ángulo. Ver Ejemplo.
Las funciones trigonométricas de los ángulos fuera del primer cuadrante se pueden determinar usando ángulos de referencia. Ver Ejemplo.
Se dice que una función es par si\(f(−x)=f(x)\) e impar si\(f(−x)=−f(x)\).
El coseno y la secante son pares; seno, tangente, cosecante y cotangente son impares.
Las propiedades pares e impares se pueden utilizar para evaluar las funciones trigonométricas. Ver Ejemplo.
La identidad pitagórica permite encontrar un coseno a partir de un seno o un seno de un coseno.
Las identidades pueden ser utilizadas para evaluar funciones trigonométricas. Ver Ejemplo y Ejemplo.
Identidades fundamentales como la Identidad Pitagórica pueden ser manipuladas algebraicamente para producir nuevas identidades. Ver Ejemplo.
Las funciones trigonométricas se repiten a intervalos regulares.
El periodo\(P\) de una función repetitiva f f es el intervalo más pequeño tal que\(f(x+P)=f(x)\) para cualquier valor de\(x\).
Los valores de las funciones trigonométricas de ángulos especiales se pueden encontrar mediante análisis matemático.
Para evaluar funciones trigonométricas de otros ángulos, podemos usar una calculadora o un software de computadora. Ver Ejemplo.

Glosario

cosecante: el recíproco de la función sinusoidal: en el círculo unitario,\( \csc t=\frac{1}{y},y≠0\)

cotangente: el recíproco de la función tangente: en el círculo unitario,\( \cot t= \frac{x}{y},y≠0\)

identidades: declaraciones que son verdaderas para todos los valores de la entrada en la que se definen

periodo: el intervalo más pequeño\(P\) de una función repetitiva\(f\) tal que\(f(x+P)=f(x)\)

secante: el recíproco de la función coseno: en el círculo unitario,\( \sec t= \frac{1}{x},x≠0 \)

tangente: el cociente del seno y el coseno: en el círculo unitario,\( \tan t= \frac{y}{x},x≠0\)

Search

Text Color

Text Size

Margin Size

Font Type