2.1: Funciones lineales

Última actualización
Guardar como PDF

Page ID: 113992

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, discutiremos las funciones lineales. Una función lineal es un polinomio con grado 1. En cálculo, aprenderás a usar líneas para aproximar funciones más complicadas con el fin de entender mejor su comportamiento en o cerca de un punto. Estas aproximaciones lineales pueden ayudarnos a evaluar los puntos cercanos sobre la función complicada más fácilmente y pueden decirnos qué tan rápido está cambiando la función. También se pueden utilizar aproximaciones lineales para ayudarnos a determinar el área de formas irregulares.

2.1.1: Propiedades de Líneas

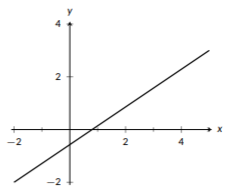
$clipboard_e6723e45dec919edcad5f610f337d25cc.png$

Figura$\PageIndex{1}$: Una línea con pendiente positiva.

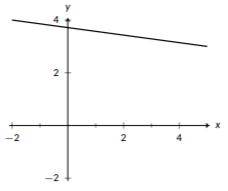
$clipboard_ea44497347beee24c7f7a708f1370cf1b.png$

Figura$\PageIndex{2}$: Una línea con pendiente negativa.

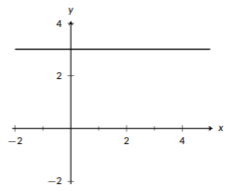
$clipboard_e428b4b1a9e86954c51b52b32d2d55d2d.png$

Figura$\PageIndex{3}$: Una línea con una pendiente de$0$.

Cada línea se puede definir de manera única en función de dos entidades de conservación: la pendiente de la línea y un punto contenido por la línea. La pendiente de la línea nos habla de su pendiente, y el punto nos da un lugar para anclar la línea. Si los puntos de una línea suben a medida que te mueves hacia la derecha, tiene una pendiente positiva, y cuanto mayor sea la pendiente, más rápido aumenta la línea, o cuanto más pronunciada es. Se puede ver un ejemplo de una línea con pendiente positiva en la Figura$\PageIndex{1}$. Si los puntos de una línea bajan a medida que te mueves hacia la derecha, tiene una pendiente negativa. Una pendiente más negativa indica que disminuye más rápido. Si los puntos no suben ni bajan a medida que te desplazas hacia la derecha, tiene una pendiente de 0, lo que indica que la línea es horizontal.

Visualmente, es sencillo determinar si la pendiente es positiva, negativa o 0. Por lo general, necesitamos información más detallada y necesitaremos calcular la pendiente. Para hacer esto a partir de una gráfica, necesitamos encontrar dos puntos en la línea. Vamos a llamar a estos dos puntos$(x_1,y_1)$ y$(x_2,y_2)$. Observe que cada punto incluye dos valores, un valor x y un valor y. Cuando eliges dos puntos, puedes usar cualquiera de los dos puntos distintos que te gusten; no importa lo que elijas siempre obtendrás el mismo resultado para la pendiente. Los matemáticos suelen utilizar$m$ como símbolo de pendiente. La fórmula es:

\[m = \frac{y_1-y_2}{x_1-x_2}\label{formula}\]

El numerador nos dice cuánto cambio tenemos en y (cambio vertical) entre los puntos y el denominador nos dice cuánto cambio tenemos en x (cambio horizontal). A veces, verás la fórmula escrita así:

\[m = \frac{\Delta y}{\Delta x}\label{change}\]

El símbolo$\Delta$ (la letra griega mayúscula “delta”) nos dice que estamos viendo el cambio, entonces$\Delta y$ significa cambio en y y$\Delta x$ significa cambios en$x$. Fórmulas$\eqref{formula}$ y$\eqref{change}$ tienen el mismo significado, simplemente se ven un poco diferentes.

Ejemplo$\PageIndex{1}$: Finding Slope

Determinar la pendiente de la línea en la Figura$\PageIndex{1}$.

Solución

Para determinar la pendiente, necesitaremos dos puntos de la gráfica. Dos puntos cualesquiera funcionarán, pero vamos a utilizar$(-2,-2)$ y$(5,3)$ ya que ambos$x$ y$y$ son valores enteros en estos puntos. Llamaremos a$(-2,2)$ nuestro primer punto; esto significa$x_1=-2$ y$y_1=-2$. Llamaremos a$(5,3)$ nuestro segundo punto; esto significa$x_2=5$ y$y_2=3$. Entonces, solo necesitamos enchufar en la fórmula para pendiente:

\[\begin{align}\begin{aligned}\begin{split} m= \frac{y_1-y_2}{x_1-x_2} & = \frac{-2-3}{-2-5} \\ & = \frac{-5}{-7} \\ & = \frac{5}{7} \end{split}\end{aligned}\end{align}\]Por lo tanto, la pendiente de la línea en la Figura$\PageIndex{1}$ es

\[m=\frac{5}{7}\]

Anteriormente, hablamos de cómo una línea se define por su pendiente y un punto, pero la pendiente misma está determinada por dos puntos en la línea. Esto significa que también podemos definir de manera única una línea a partir de dos puntos que están en la línea. Podemos tomar ambos para encontrar la pendiente, y luego usar cualquiera de los puntos como nuestro ancla.

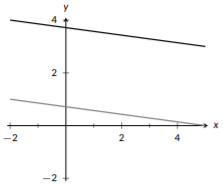
$clipboard_eeeb3188acafe33e5782cb2cec766bad0.png$

Figura$\PageIndex{4}$: Líneas paralelas.

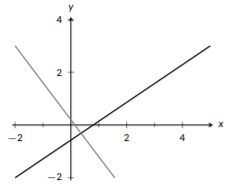
$clipboard_e347c9367ca681d8270b06816be08c14f.png$

Figura$\PageIndex{5}$: Líneas perpendiculares.

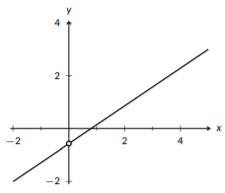
$clipboard_eec9858f984cca046483b76e80d649fd2.png$

Figura$\PageIndex{6}$: La$y$ intersección de una línea.

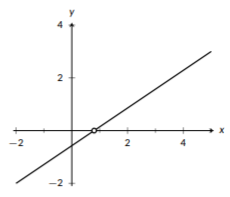
$clipboard_e3b8fad4ecede160ad310b11cbc24683b.png$

Figura$\PageIndex{7}$: La$x$ intersección de una línea.

Si dos líneas tienen la misma pendiente, decimos que son paralelas. Las líneas paralelas nunca se cruzarán entre sí ya que tienen la misma pendiente (a menos que sean realmente la misma línea). Si dos líneas no son paralelas, tienen que intersecarse en un punto. Si las líneas forman un ángulo recto ($90^{\circ}$) cuando se cruzan, son perpendiculares. Al igual que las líneas paralelas donde$m_1=m_2$ (la pendiente de la línea 1 es la misma que la pendiente de la línea 2), las líneas perpendiculares también tienen pendientes relacionadas. Aquí, si la línea 1 y la línea 2 son perpendiculares,$m_1 =-\frac{1}{m_2}$. Podríamos reorganizar esta ecuación para resolverla$m_2$ y obtendríamos$m_2 = -\frac{1}{m_1}$. Observe que la fórmula se ve igual, excepto$m_1$ y$m_2$ se intercambian. Esta relación se describe como “recíproco negativo”; negativo ya que el signo es opuesto y recíproco ya que invertimos la relación. Veremos esta propiedad utilizada en el ejemplo$\PageIndex{4}$.

Cuando miramos una línea, podemos usar dos puntos cualesquiera para describirla, pero hay dos puntos que los matemáticos tienen más probabilidades de usar. La primera (y más utilizada) es la intersección y. Este es el punto donde la línea cruza (“intercepta”) el eje y. Ya que$x=0$ en el eje y, este punto se ve así$(0,y_{int})$. De igual manera, la intercepción x se usa frecuentemente. La intersección x es el punto donde la línea cruza el eje x, por lo que tiene$y=0$ y se ve como$(x_{int},0)$. Estos dos puntos son de uso común porque son más fáciles de trabajar ya que una de las coordenadas es 0.

2.1.2: Expresar funciones lineales

Hay dos formas comunes de expresar funciones lineales, forma punto-pendiente y forma pendiente-intercepción. Como probablemente puedas adivinar por los nombres, ambas formas requerirán que primero conozcas la pendiente. La forma pendiente-intersección requiere conocer la intersección y de la función, y la forma punto-pendiente le permite usar cualquier punto en la línea. Es bueno estar cómodo trabajando con ambas formas y cambiando entre ellas porque a veces una forma será más útil que la otra. En el cálculo, la forma de punto-pendiente suele ser útil porque veremos líneas sobre una pequeña región que no siempre contendrá la intercepción y de la línea. La forma pendiente-intersección es:

\[\label{eqn:slope_intercept_form} y=mx+b\]

donde$m$ está la pendiente de la función y$b$ es la coordenada y de la intersección y. La forma de pendiente puntual es:

\[\label{eqn:point_slope_form} y-y_1 = m(x-x_1)\]

donde$m$ está la pendiente y$(x_1,y_1)$ es cualquier punto de la línea. Echemos un vistazo a un ejemplo de cómo trabajar con ambas formas.

Ejemplo$\PageIndex{2}$: Writing an Equation for a Line

Escribe la ecuación para la línea que pasa a través$(2,4)$ y es paralela$3x+y=6$ en forma de pendiente-intersección.

Solución

Analicemos la información que tenemos hasta el momento. Primero, sabemos que nuestra línea pasa por el punto$(2,4)$. Sabemos que también necesitamos su pendiente.

Nos dicen que es paralelo a$3x+y=6$, así que tendrá la misma pendiente que esa línea. Sin embargo, esta línea no está en ninguna de nuestras formas, por lo que no queda claro de inmediato cuál es la pendiente. Empezaremos poniendo esta línea,$3x+y=6$ en forma de pendiente-intercepción (porque requiere menos álgebra que ponerla en forma de punto-pendiente). Para ponerlo en forma de pendiente-intercepción, necesitamos aislarlo$y$. Eso lo haremos restando$3x$ de ambos lados. Eso da\[y=6-3x\]

Si reorganizamos el lado derecho, obtenemos$y=-3x+6$. Ahora, está en forma de pendiente-intersección y podemos ver que la pendiente está$-3$.

Ahora, tenemos la pendiente de nuestra línea,$m=-3$, y un punto en nuestra línea$(2,4)$, y nuestro objetivo es expresar la línea en forma de pendiente-intercepción. Hay un pequeño problema con esto- no sabemos la intercepción y. Por suerte, tenemos suficiente información para expresar la línea en forma de punto-pendiente, así que comenzaremos con eso y usaremos álgebra para ponerla en forma de pendiente-intercepción. En forma de punto-pendiente, tenemos:\[y-4=-3(x-2)\]

Usaremos álgebra para reescribir esto en forma de pendiente-intercepción (es decir, aislaremos y):\[\begin{align}\begin{aligned}\begin{split} y-4 & = -3x+6 \\ y & = -3x+6+4 \\ y & = -3x+10 \end{split}\end{aligned}\end{align}\]

Entonces, en forma de pendiente-intercepción, la línea es$y=-3x+10$. Esto también nos dice que la intersección y de esta línea es$(0,10)$. Nuestra respuesta final, en forma de pendiente-intercepción, es

\[y=-3x+10\]

Esta no es la única manera de responder a esta pregunta, así que probemos un segundo método. Los dos métodos siempre te darán el mismo resultado, por lo que es totalmente una cuestión de preferencia a la hora de elegir qué método usar.

Ejemplo$\PageIndex{3}$: Writing an Equation for a Line- A Second Method

Escribe la ecuación para la línea que pasa a través$(2,4)$ y es paralela$3x+y=6$ en forma de pendiente-intersección.

Solución

De nuestro trabajo anterior sobre este problema, sabemos que nuestra línea pasa por el punto$(2,4)$ y que tiene una pendiente de$-3$. También sabemos que la forma de pendiente-intercepción se parece\[y=mx+b\]

y que esta declaración se sostiene por cada$(x,y)$ par que se encuentre en la línea. Lo sabemos$m$, pero nos falta$b$. No obstante, sí sabemos que$(2,4)$ está en la línea, entonces\[y=-3x+b\]

necesita ser verdad para$x=2$ y$y=4$. Sustituiremos estos valores en nuestra ecuación y resolveremos$b$:\[\begin{align}\begin{aligned}\begin{split} 4 & =-3(2)+b\\ 4 & = -6 + b\\ 10 & = b \end{split}\end{aligned}\end{align}\]

Ahora, ya sabemos$b$, así que nuestra respuesta final, en forma de pendiente-intercepción, es de nuevo

Veamos un ejemplo más, esta vez trabajando con una línea perpendicular.

Ejemplo$\PageIndex{4}$: Perpendicular Line

En forma pendiente-intercepción, escriba la ecuación de una línea con una intersección y de 5 que sea perpendicular a$y-4=6(x-2)$.

Solución

Veamos la información que tenemos hasta el momento. Nos dicen que la línea que nos interesa tiene una intercepción en y de 5. Sabemos que$x=0$ para la intercepción y, entonces esto realmente significa que la intercepción y es el punto$(0,5)$. A continuación, sabemos que estamos perpendiculares a la línea$y-4=6(x-2)$. Esta línea se da en forma de punto-pendiente y tiene una pendiente de 6.

La pendiente de nuestra línea tiene que ser$-\frac{1}{6}$ ya que es perpendicular a una línea con una pendiente de 6. En general, eso nos da que la ecuación de nuestra línea, en forma de pendiente-intersección, es

\[y=-\frac{1}{6}x+5\]