5.6: Análisis costo-volumen-beneficio en planeación
- Page ID
- 63987
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Análisis costo-volumen-beneficio (CVP)
Las empresas utilizan el análisis costo-volumen-beneficio (CVP) (también llamado análisis de equilibrio) para determinar qué afecta los cambios en sus precios de venta, costos y/o volumen que tendrán sobre las ganancias a corto plazo. Un análisis cuidadoso y preciso de costo-volumen-beneficio (CVP) requiere el conocimiento de los costos y su comportamiento fijo o variable como cambios de volumen.
Un gráfico costo-volumen-beneficio es un gráfico que muestra las relaciones entre ventas, costos, volumen y ganancias. Mira la ilustración a continuación. La ilustración muestra una tabla costo-volumen-beneficio para Video Productions, una compañía que produce DVD. Cada DVD se vende por $20. El costo variable por DVD es de $12, y los costos fijos mensuales son de $40,000.
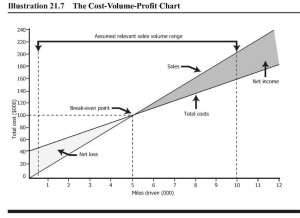
La línea de costo total representa los costos fijos de $40,000 más $12 por unidad. De esta manera, si Video Productions produce y vende 6,000 DVDs, los costos totales de la compañía son de $112,000, conformados por $40.000 costos fijos y $72,000 costos variables totales ($72,000 = $12 por unidad X 6,000 unidades producidas y vendidas).
La línea de ingresos totales muestra cómo los ingresos aumentan a medida que aumenta el volumen. El ingreso total es de $120,000 por ventas de 6,000 cintas ($20 por unidad X 6,000 unidades vendidas). En el gráfico, demostramos el efecto del volumen en los ingresos, costos e ingresos netos, para un precio particular, costo variable por unidad y costo fijo por periodo.
En cada volumen, se pueden estimar las ganancias o pérdidas de la compañía. Por ejemplo, a un volumen de 6 mil unidades, la ganancia es de $8,000. Podemos encontrar el ingreso neto ya sea construyendo una cuenta de resultados o usando la ecuación de ganancias. La cuenta de resultados del margen de contribución da los siguientes resultados para un volumen de 6,000 unidades:
| Ingresos | $120,000 |
| Menos: costos variables | 72,000 |
| Margen de contribución | 48,000 |
| Menos: Costos fijos | 40,000 |
| Ingresos netos | $ 8,000 |
Hemos introducido un nuevo término en esta declaración de ingresos: el margen de contribución. El margen de contribución es el monto por el cual los ingresos superan los costos variables de producción de esos ingresos. Podemos calcularlo por unidad o volumen total de ventas. Por unidad, el margen de contribución para Producciones de Video es de $8 (el precio de venta de $20 menos el costo variable por unidad de $12).
| Margen de Contribución = | Ventas — Costo Variable |
El margen de contribución indica la cantidad de dinero restante después de que la compañía cubra sus costos variables. Este resto contribuye a la cobertura de los costos fijos y al ingreso neto. En la cuenta de resultados de Video Production, el margen de contribución de $48,000 cubre los $40,000 costos fijos y deja $ 8,000 en ingresos netos.
También puede calcular una relación de margen de contribución utilizando la siguiente fórmula:
| Cotización Margen RATIO | Ventas — Costo Variable |
| Ventas |
Mira este video para ver más sobre el margen de contribución y cómo se puede usar en los negocios.
Un elemento de YouTube ha sido excluido de esta versión del texto. Puedes verlo en línea aquí: pb.libretexts.org/llmanagerialaccounting/? p=118
Ecuación de ganancias La ecuación de ganancias es igual que la cuenta de resultados, excepto que presenta el análisis en una forma ligeramente diferente. Según la ecuación de ganancias:
Ingresos netos = Ingresos — Costos variables totales — Costos fijos
Para Video Productions, la ecuación de ganancias se ve así:
Ingreso neto = $120,000 − $72,000 − $40,000 Ingresos
netos = $8,000
El gráfico CVP anterior muestra los datos de costo para Producciones de Video en un rango relevante de salida de 500 a 10,000 unidades. Recordemos que el rango relevante es el rango de producción o volumen de ventas sobre el cual se cumplen los supuestos básicos de comportamiento de costos. Para volúmenes fuera de estos rangos, los costos se comportan de manera diferente y alteran las relaciones asumidas Por ejemplo, si Video Productions producía y vendía más de 10,000 unidades mensuales, podría ser necesario aumentar la capacidad de la planta (incurriendo así en costos fijos adicionales) o trabajar turnos adicionales (incurriendo así en cargos por horas extras y otras ineficiencias). En cualquier caso, las relaciones de costo asumidas ya no serían válidas.
La cuenta de resultados del margen de contribución se utiliza con bastante frecuencia ya que separa los costos fijos y variables para permitir que una empresa vea qué puede cambiar directamente y qué no puede cambiar. Este video te dará un ejemplo del por qué y cómo hacer una cuenta de resultados con margen de contribución.
Un elemento de YouTube ha sido excluido de esta versión del texto. Puedes verlo en línea aquí: pb.libretexts.org/llmanagerialaccounting/? p=118
- Principios Contables: Una Perspectiva Empresarial. Autor: James Don Edwards, Universidad de Georgia & Roger H. Hermanson, Universidad Estatal de Georgia.. Proporcionado por: Endeavour International Corporation. Proyecto: El Proyecto de Texto Global. Licencia: CC BY: Atribución
- Video de Investopedia: Margen de contribución. Autor: Investopedia. Ubicado en: Youtu.be/pm6eo9qiuiy. Licencia: Todos los Derechos Reservados. Términos de licencia: Licencia estándar de YouTube
- Cuenta de ingresos con margen de contribución. Autor: Krisitin Ingram. Ubicado en: Youtu.be/fyaevkcsjci. Licencia: Todos los Derechos Reservados. Términos de licencia: Licencia estándar de YouTube