5.7: Punto de ruptura — par para un solo producto
- Page ID
- 63963
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encontrar el punto de equilibrio
Una empresa rompe el equilibrio durante un período determinado cuando los ingresos por ventas y los costos cobrados a ese período son iguales. Así, el punto de equilibrio es ese nivel de operaciones en el que una empresa no se da cuenta de ingresos ni pérdidas netas.
Una compañía puede expresar un punto de equilibrio en dólares de ingresos por ventas o número de unidades producidas o vendidas. No importa cómo una empresa exprese su punto de equilibrio, sigue siendo el punto de cero ingresos o pérdidas. Para ilustrar el cálculo de un punto de equilibrio mira el siguiente video y luego trabajaremos con la compañía anterior, Video Productions.
Un elemento de YouTube ha sido excluido de esta versión del texto. Puedes verlo en línea aquí: pb.libretexts.org/llmanagerialaccounting/? p=120
Antes de que podamos comenzar, necesitamos dos cosas de la página anterior: Margen de Contribución por unidad y RATIO de Margen de Contribución. Estas fórmulas son:
| Margen de contribución por unidad = | Precio de Venta — Costo Variable por Unidad |
| Relación Margen de Contribución = | Margen de contribución (Ventas — Costo Variable) |
| Ventas |
Break-even en unidades
Recordemos que Video Productions produce DVD que se venden por $20 por unidad. Los costos fijos por periodo suman 40,000 dólares, mientras que el costo variable es de 12 dólares por unidad. Calculamos el punto de equilibrio en unidades como:
| Unidades BE
= |
Costos Fijos |
| Margen de contribución por unidad |
El margen de contribución de Video Producciones por unidad es de $8 ($20 precio de venta por unidad — $12 costo variable por unidad). El punto de equilibrio en unidades se calcularía como:
| Unidades BE = | Costos Fijos | $40.000 | = 5,000 unidades |
| Margen de contribución por unidad | $8 |
El resultado nos dice que Producciones de Video rompe el par a un volumen de 5 mil unidades mensuales. Podemos demostrar que eso es cierto calculando los ingresos y los costos totales en un volumen de 5,000 unidades. Ingresos = (5,000 unidades X $20 precio de venta por unidad) $100,000. Costos totales = $100,000 ($40,000 costos fijos + $60,000 costos variables calculados como $12 por unidad X 5,000 unidades).
Mire el gráfico costo-volumen-beneficio y tenga en cuenta que las líneas de ingresos y costos totales se cruzan en 5,000 unidades, el punto de equilibrio. Video Productions tiene ingresos netos en volúmenes mayores a 5 mil, pero tiene pérdidas en volúmenes menores a 5 mil unidades.
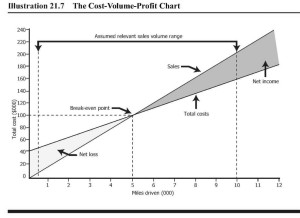
Punto de equilibrio en dólares de ventas Las empresas frecuentemente piensan en volumen en dólares de ventas en lugar de unidades. Para una empresa como GM que fabrica Cadillacs y ciertos componentes pequeños, no tiene sentido pensar en un punto de equilibrio en unidades. GM rompe el par en dólares de ventas.
La fórmula para calcular el punto de equilibrio en dólares de ventas se parece mucho a la fórmula para calcular el punto de equilibrio en unidades, excepto que dividimos los costos fijos por la relación de margen de contribución en lugar del margen de contribución por unidad.
La relación de margen de contribución expresa el margen de contribución como porcentaje de ventas. Para calcular esta relación, divida el margen de contribución por unidad entre el precio de venta por unidad, o el margen de contribución total por los ingresos totales. La relación de margen de contribución de Video Production es:
| Relación Margen de Contribución = | Margen de contribución | $8 | = 0.4 o 40% |
| Ventas | $20 |
O bien, refiriéndose a la cuenta de resultados en la que Video Productions tuvo un margen de contribución total de $48,000 sobre ingresos de $120,000, calculamos la relación de margen de contribución como margen de contribución $48,000/Ingresos $120,000 = 0.40 o 40%.
Es decir, por cada dólar de ventas, quedan $0.40 después de costos variables para contribuir a cubrir costos fijos y generar ingresos netos.
Usando esta relación de margen de contribución, calculamos el punto de equilibrio de Producción de Video en dólares de ventas como:
| BE en Dólares de Ventas = | Costos Fijos | $40.000 | = $100,000 |
| RATIO de Margen | 0.40 |
El volumen de equilibrio de ventas es de $100,000 ( también se puede calcular como punto de equilibrio en unidades 5,000 unidades x precio de venta $20 por unidad). En este nivel de ventas, los costos fijos más los costos variables equivalen a ingresos por ventas, como se muestra aquí:
| Ingresos | $100,000 | (5,000 unidades x $20 por unidad) |
| Menos: costos variables | 60,000 | (5,000 unidades x $12 por unidad) |
| Margen de contribución | 40,000 | (100.000 — 60.000) |
| Menos: Costos fijos | 40,000 | |
| Ingreso Neto | $0 |
Margen de Seguridad
Si las ventas actuales de una compañía son más que su punto de equilibrio, tiene un margen de seguridad igual a las ventas actuales menos las ventas de equilibrio. El margen de seguridad es la cantidad por la cual las ventas pueden disminuir antes de que la empresa incurra en una pérdida. Por ejemplo, supongamos que Video Productions actualmente tiene ventas de 120,000 dólares y sus ventas de equilibrio son de 100,000 dólares. El margen de seguridad es de $20,000, calculado de la siguiente manera:
Margen de seguridad = Ventas actuales — Ventas de equilibrio
Margen de seguridad = $120,000 — $100,000 = $ 20,000
En ocasiones las personas expresan el margen de seguridad como un porcentaje, llamado el margen de tasa de seguridad o simplemente margen de porcentaje de seguridad. El margen de tasa de seguridad es igual a
| Margen de Porcentaje de Seguridad = | Ventas actuales — Ventas de equilibrio |
| Ventas Actuales |
Usando los datos recién presentados, calculamos el margen de tasa de seguridad es de $20,000/120,000 = 16.67%
Esto significa que el volumen de ventas podría caer 16.67 por ciento antes de que la compañía incurriera en una pérdida.
Beneficio o
ingreso objetivo
También puedes usar este mismo tipo de análisis para determinar cuántas unidades de venta o dólares de ventas necesitarías para obtener una ganancia específica (¡muy útil!). La buena noticia es que ya aprendiste la fórmula básica, apenas la estamos cambiando ligeramente. Las fórmulas que necesitaremos son:
| Unidades al Objetivo de Beneficio = | Costos Fijos + Ingresos Objetivo |
| Margen de contribución por unidad |
| Dólares de ventas para beneficio objetivo = | Costos Fijos + Ingresos Objetivo |
| RATIO de Margen |
Estos parecen familiares (¡o deberían!). Estas son las mismas fórmulas que utilizamos para el análisis de equilibrio pero esta vez hemos agregado ingresos objetivo. Si lo piensas, ES la misma fórmula porque al descanso incluso nuestro ingreso objetivo es CERO.
Un elemento de YouTube ha sido excluido de esta versión del texto. Puedes verlo en línea aquí: pb.libretexts.org/llmanagerialaccounting/? p=120
Veamos otro ejemplo. La dirección de una importante aerolínea desea saber cuántos asientos se deben vender en el Vuelo 529 para obtener $8,000 en ganancias. Para resolver este problema, la gerencia debe identificar y separar los costos en categorías fijas y variables.
Los costos fijos del Vuelo 529 son los mismos independientemente del número de asientos ocupados. Los costos fijos incluyen el combustible requerido para volar el avión y la tripulación (sin pasajeros) a su destino; la depreciación del avión utilizado en el vuelo; y los salarios de los tripulantes requeridos, los asistentes de puerta y el personal de mantenimiento y reabastecimiento de combustible. Los costos fijos son $12,000.
Los costos variables varían directamente con el número de pasajeros. Los costos variables incluyen refrigerios y bebidas proporcionados a los pasajeros, costos de manejo de equipaje y el costo del combustible adicional requerido para volar el avión con pasajeros a su destino. La gerencia expresaría cada costo variable por pasajero. Los costos variables son $25 por pasajero.
Los boletos se venden por $125 cada uno. El margen de contribución es de $100 ($125 ventas — $25 variable) y la relación de margen de contribución es de 80% (margen de contribución de $100 /$125 ventas). Podemos calcular las unidades y el dólar de ventas requerido para obtener $8,000 en ganancias por:
| Unidades al Objetivo de Beneficio = | Costos Fijos + Ingresos Objetivo | = 12,000 + 8,000 | = $20,000 | = 200 boletos |
| Margen de contribución por unidad | $100 | $100 |
Los dólares de venta requeridos podrían calcularse como unidades de equilibrio de 200 boletos x $125 precio de venta por boleto = $25,000 o usando la siguiente fórmula:
| Dólares de ventas para beneficio objetivo = | Costos Fijos + Ingresos Objetivo
= |
12,000 + 8,000 = |
$20,000 | = $25,000 |
| RATIO de Margen | 0.80 | 0.80 |
La administración también puede utilizar su conocimiento de las relaciones costo-volumen-beneficio para determinar si aumentar los costos de promoción de ventas en un esfuerzo por aumentar el volumen de ventas o aceptar un pedido a un precio inferior al habitual. En general, el estudio cuidadoso del comportamiento de costos ayuda a la gerencia a planificar futuros cursos de acción.
- Principios Contables: Una Perspectiva Empresarial. Autor: James Don Edwards, Universidad de Georgia & Roger H. Hermanson, Universidad Estatal de Georgia.. Proporcionado por: Endeavour International Corporation. Proyecto: El Proyecto de Texto Global.. Licencia: CC BY: Atribución
- Análisis de ganancias por volumen de costos (CVP): cálculo del punto de equilibrio. Autor: Education Unlocked. Ubicado en: Youtu.be/NW2IIOAF6LC. Licencia: Todos los Derechos Reservados. Términos de licencia: Licencia estándar de YouTube
- Análisis de ganancias por volumen de costos (CVP): Utilidad neta objetivo. Autor: Education Unlocked. Ubicado en: Youtu.be/4u60ya5ysmu. Licencia: Todos los Derechos Reservados. Términos de licencia: Licencia estándar de YouTube