16: Análisis de Préstamos
- Page ID
- 67958
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
Después de completar este capítulo, debe ser capaz de: (1) comprender las diferentes formas en que se pueden calcular los intereses de un préstamo; (2) reconocer los diferentes tipos de tasas de interés que se utilizan para calcular los costos de interés de los préstamos; (3) tasas de interés comparables por computadora al encontrar un préstamo efectivo tasa de interés; (4) usar hojas de Excel para calcular el pago del préstamo, tasa de interés, plazo, elasticidad de plazo y cronograma de amortización para un préstamo en particular; y (5) evaluar préstamos alternativos utilizando modelos de valor presente (PV) desarrollados anteriormente.
Para lograr tus metas de aprendizaje, debes completar los siguientes objetivos:
- Conozca las diferencias entre las siguientes tasas de interés: la tasa porcentual anual (TAE), la tasa actuarial y la tasa efectiva.
- Aprende a calcular la TAE, la tasa actuarial y la tasa efectiva en préstamos alternativos.
- Aprenda a usar la ecuación de igualdad de préstamo para encontrar la tasa de interés efectiva de un préstamo, su pago constante, su plazo y su monto original del préstamo.
- Aprenda a encontrar la relación de elasticidad entre las tasas de interés, los pagos de préstamos y el plazo del préstamo de pago constante.
- Aprende a crear una tabla de amortización para préstamos de pago constante.
- Aprende a encontrar puntos de equilibrio para refinanciar préstamos.
- Aprende a encontrar la tasa efectiva para varios préstamos con tasa de interés disfrazados, incluyendo préstamos de descuento y préstamos con puntos agregados .
Introducción
Las fórmulas de préstamo y los modelos PV tienen muchas similitudes. Las tasas de interés de los préstamos son como costos de oportunidad, el monto del préstamo es como una inversión y los pagos de préstamos son como el flujo de caja de una inversión. Estas y otras similitudes entre los modelos fotovoltaicos y las fórmulas de préstamo nos permiten utilizar herramientas fotovoltaicas para analizar diferentes tipos de préstamos. La siguiente sección se centra en las definiciones alternativas de tasas de interés. En este capítulo también se identificará la relación entre el plazo de un préstamo y el tamaño del pago del préstamo. Por último, este capítulo encuentra puntos de equilibrio al refinanciar préstamos y tasas de interés efectivas para una variedad de préstamos con tasas de interés disfrazadas.
Comparación de la Tasa Actuarial, la Tasa de Porcentaje Anual (TAE) y la Tasa de Interés Efectiva
Los préstamos cobran tasas de interés de las cuales hay al menos tres tipos que están estrechamente relacionados entre sí. Estas tarifas y sus sinónimos de uso común se enumeran a continuación. El nombre de la tasa de interés utilizado en este capítulo está en cursiva. Son: (1) tasa actuarial, tasa compuesta, tasa verdadera o tasa periódica; (2) Tasa de Porcentaje Anual (TAE), tasa anual o tasa nominal; y (3) tasa de interés efectiva o tasa anual efectiva.
Tasa Actuarial. En las transacciones financieras, los intereses pueden ser calculados y cobrados más de una vez al año. Por ejemplo, los intereses sobre los depósitos de ahorro generalmente se calculan diariamente mientras que muchos bonos corporativos pagan intereses semestrales. La tasa de interés utilizada en los cómputos para periodos menores a un año se denomina tasa de interés actuarial. La tasa actuarial se define como la tasa de interés por periodo compuesto o la tasa de interés por periodo de conversiones. Es la tasa actuarial utilizada para cobrar intereses sobre la suma principal durante cada periodo de conversión sucesivo. Por ejemplo, considere una tasa actuarial de 1% cobrada mensualmente en $1,000. En este caso, en el primer mes del préstamo, se cobra 1% de $1,000 o $10 de interés. En el segundo mes, los intereses se cobran sobre $1,010 igual a $10.10, etc.
Tasa de Porcentaje Anual (TAE). Que r f represente la TAE. Dejar que m signifique el número de veces durante el año en que se calcula o cobra el interés. Así, m es igual al número de periodos compuestos por año. La relación de r f/m es la tasa actuarial, la tasa compuesta, la tasa verdadera o la tasa periódica.
Encontramos la TAE a partir de tasas actuariales expresando la tasa actuarial sobre una base anual. Para convertir la tasa actuarial a una TAE, multiplicamos la tasa actuarial por m. En el ejemplo anterior, multiplicamos la tasa actuarial de 1% mensual por 12 para producir una TAE de 12%. Cuando el periodo compuesto o periodo de conversión es de un año de duración, entonces la tasa actuarial y la TAE son iguales.
Considera dos instituciones de ahorro, ambas ofreciendo la misma APR. La única diferencia es que la institución A ofrece una composición mensual de intereses, mientras que la institución B ofrece una composición anual. ¿Cuál debería preferir el ahorrador? Obviamente, se prefiere la capitalización mensual porque el ahorrador gana intereses sobre los intereses ganados durante el mismo año. Con la institución B, los intereses se devengan durante el año únicamente sobre el principal ahorrado y sobre los intereses devengados en años anteriores.
Tasas de interés efectivas. Las tasas de interés efectivas son los intereses reales cobrados medidos anualmente. Cuando las APR tienen diferentes números de períodos compuestos por año, las diferentes tasas actuariales deben convertirse a sus tasas de interés efectivas para su comparación. La tasa efectiva se obtiene componiendo la tasa actuarial por un periodo de un año. A medida que aumenta el número de periodos compuestos por año, aumenta la diferencia entre la TAE y la tasa efectiva.
Relación entre las tasas de interés. Las relaciones entre una tasa actuarial, una TAE y una tasa efectiva pueden resumirse fácilmente. Sea m el número de periodos compuestos por año, que r f sea la TAE, que r f /m sea la tasa actuarial, y dejar que re sea la tasa efectiva. La relación entre la tasa efectiva r e, la tasa de TAE r f y la tasa actuarial r f /m se puede expresar como:
\ [r^ {e} =\ izquierda [\ izquierda (1+\ frac {r^ {f}} {m}\ derecha) ^ {m} -1\ derecha] \ etiqueta {16.1}\]
Obsérvese que cuando m = 1, la tasa de interés efectiva, la tasa de TAE y la tasa actuarial son iguales. Sin embargo, cuando m no es 1, las tarifas ya no son iguales. Por ejemplo, supongamos que deseamos encontrar la re asumiendo r f se compusieron trimestralmente. Para resolver este problema vamos a m = 4, y r f = 12. Sustituyendo .12 por r f y 4 por m en la Ecuación\ ref {16.1}, obtenemos los resultados descritos en la Tabla 16.1 usando Microsoft Excel. En la celda B3 ingresamos la función f x = ((1 + (B1/B2)) ^B2) — 1 que devuelve 12.55%.
| B4 | Función: | = (1+B2/B3) ^B3 -1 | |
|---|---|---|---|
| A | B | C | |
| 1 | Encontrar una tasa de interés efectiva | ||
| 2 | ABR | 0.12 | |
| 3 | m | 4 | |
| 4 | tasa efectiva | 12.55% | “= (1 + abr/m) ^m — 1 |
Si m se incrementa a 12, o periodos compuestos mensuales, la tasa efectiva se encuentra como antes. Sea m = 12, y r f = 12 en la Ecuación \ ref {16.1}. Entonces
\ [\ izquierda [\ izquierda (1+\ frac {.12} {12}\ derecha) ^ {12} -1\ derecha] \ etiqueta {16.2}\]
Para resolver esta ecuación en Excel, cambiamos la celda B3 a 12 y encontramos que la tasa de interés efectiva es igual a 12.68% como se muestra en la Tabla 16.2.
| B4 | Función: | = (1+B2/B3) ^B3 -1 | |
|---|---|---|---|
| A | B | C | |
| 1 | Encontrar una tasa de interés efectiva | ||
| 2 | ABR | 0.12 | |
| 3 | m | 12 | |
| 4 | tasa efectiva | 12.68% | “= (1 + abr/m) ^m — 1 |
Se obtiene una fórmula especial de composición al permitir que el número de períodos compuestos sea muy grande. Esta idea se expresa como:
(16.3)
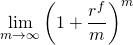
lo que significa que a medida que m se acerca al infinito la tasa efectiva re equivale a:
(16.4)
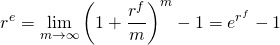
Para resolver este problema usando Excel, utilizamos la función EXP. En Excel, el número “e” de Euler se encuentra como la función EXP (1) y 12% compuesto continuamente se puede calcular como f x = EXP (.12) — 1 = 12.75. Usando la designación de celda anterior, para encontrar el valor de composición continua de 12% entraríamos la fórmula en B4 como: f x = EXP (B2) — 1 = 12.75.
| B4 | Función: | =EXP (B2) — 1 | |
| A | B | C | |
| 1 | Encontrar una tasa de interés efectiva | ||
| 2 | APR | 0.12 | |
| 3 | m | Infinito | |
| 4 | tasa efectiva | 12.75% | “=EXP (TAE) — 1 |
Préstamos de Pago Constante
Habiendo definido las tasas de interés en los modelos financieros, ahora utilizamos modelos PV para analizar el tipo de préstamo más común, el préstamo de pago constante. Los préstamos de pago constante se reembolsan con una serie de pagos iguales A a intervalos de tiempo iguales. Estos pagos pueden ocurrir m veces durante un año a lo largo de n años, lo que arroja un total de mn pagos.
La igualdad fundamental es que la suma de los pagos del
préstamo descontados a la tasa de interés actuarial debe ser igual a
la cantidad prestada. La relación entre el monto del préstamo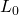 ,,
recibido en el periodo de tiempo cero, con el pago A, realizado por
mn periodos, a tasa de interés actuarial
(r f /m) a partir del periodo uno, es:
,,
recibido en el periodo de tiempo cero, con el pago A, realizado por
mn periodos, a tasa de interés actuarial
(r f /m) a partir del periodo uno, es:
\ [L_ {0} =\ frac {A} {1+\ frac {r^ {f}} {m}} +\ frac {A} {\ left (1+\ frac {r^ {f}} {m}\ derecha) ^ {2}} +\ puntos+\ frac {A} {\ izquierda (1+\ frac {r^ {r ^ {f}} {m} derecha) ^ {m n}}\ etiqueta {16.5}\]
En esta fórmula, la tasa actuarial (r f /m) es la TIR para el modelo PV, y como los pagos del préstamo son constantes, es único.
Una suma que resultará útil en varios cálculos es la siguiente:
(16.6)
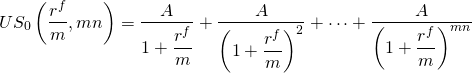
La notación US 0 (r f /m, mn) representa el valor actual de una serie uniforme de pagos de $1 descontados a la tasa actuarial (r f /m) por periodos (mn). Esta notación taquigráfica nos permite reescribir la ecuación \ ref {16.2} como:
(16.7)
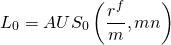
Recordemos que con una ecuación podemos resolver para como máximo una variable desconocida. De la Ecuación\ ref {16.7} si conocemos A y US 0 (r f /m, mn) podemos encontrar monto de préstamo L 0 que mn pagos de monto A descontados a tasa actuarial (r f /m) serán reembolse.
Supongamos que resolvemos para A en la Ecuación \ ref {16.7}. El resultado es:
(16.8)
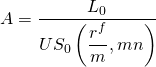
De la Ecuación\ ref {16.8} si conocemos L 0 y US 0 (r f /m, mn), podemos encontrar el pago constante del préstamo A, que, si se descuenta a tasa actuarial (r f /m) por mn periodos, devolverá monto del préstamo L 0.
Supongamos que resolvemos para US 0 (r f /m, mn) en la Ecuación \ ref {16.7}. El resultado es:
(16.9)
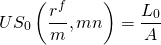
Si conocemos A y monto del préstamo L 0 en Ecuación\ ref {16.9} podemos encontrar r f, m, o n, ese pago constante del préstamo A descontado a tasa actuarial (r f /m) para mn periodos se amortizarán.
Afortunadamente, los cálculos descritos en las ecuaciones (16.7), (16.8) y (16.9) se pueden realizar fácilmente usando Excel.
Ejemplo\(\PageIndex{1}\): Monto del préstamo soportado por un préstamo de pago constante
Supongamos que un prestatario puede realizar pagos constantes de $150 mensuales durante 48 meses (cuatro años). El prestatario quiere saber qué tamaño de préstamo se puede reembolsar si la tasa de interés TAE es del 5% y la tasa actuarial es .05/12 = 0.42%. Usando la ecuación\ ref {16.8} podemos resolver el monto del préstamo soportado por el pago constante del préstamo de $150 usando la siguiente fórmula:
(16.10)
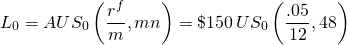
Resolvemos la ecuación anterior usando la función PV de Excel en la Tabla 16.4.
| B7 | Función: | =PV (B3/B4, B4*B5, B6, ,0) | |
| A | B | C | |
| 1 | Encontrar el monto del préstamo en un préstamo de pago constante | ||
| 2 | |||
| 3 | tasa | .05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | pmt | -150 | |
| 7 | PV | $6,513.44 | “=PV (tasa/m, mn, pmt, ,0) |
La respuesta que se muestra es: $6,513.44. Es decir, 48 pagos mensuales de $150 sobre un préstamo cobrando una tasa de interés APR del 5% y una tasa de interés actuarial mensual de .42%, devolverán un préstamo por la cantidad de $6,513.44.
Ejemplo\(\PageIndex{2}\): Anualidades de Préstamo de Pago Constante
Supongamos que se toman prestados $5,000 de una institución crediticia por cinco años a una TAE de 12% o a una tasa actuarial mensual de 1%. El préstamo se va a reembolsar con 60 cuotas mensuales iguales. ¿Cuál es el pago o anualidad necesaria para retirar el préstamo?
Usando la ecuación\ ref {16.4} podemos resolver para el pago que reembolsa el préstamo de $5,000:
(16.11)
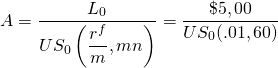
Resolvemos para el pago del préstamo utilizando la función PMT de Excel en la Tabla 16.5. La respuesta que se muestra es: —$111.22 lo que significa que 60 pagos de $111.22 sobre un préstamo cobrando 12% de interés APR y una tasa de interés actuarial mensual del 1%, devolverán un préstamo por la cantidad de $5,000.
| B6 | Función: | =PV (B3/B4, B4*B5, B7, ,0) | |
| A | B | C | |
| 1 | Encontrar el monto del préstamo en un préstamo de pago constante | ||
| 2 | |||
| 3 | tasa | 0.12 | |
| 4 | m | 12 | |
| 5 | n | 5 | |
| 6 | pmt | ($111.22) | “=pmt (tasa/m, mn, PV, ,0) |
| 7 | PV | $5,000.00 | |
Ejemplo 16.3. Plazo de préstamo requerido para retirar un préstamo de pago constante. Supongamos que un prestatario puede realizar pagos constantes de $150 mensuales. El prestatario quiere saber cuántos pagos mensuales se requerirán para retirar un préstamo de $8,000 si la tasa de interés TAE es de 6% y la tasa actuarial mensual es de .5%. Usando la ecuación\ ref {16.9} podemos resolver el plazo del préstamo requerido para retirar el préstamo.
(16.12)
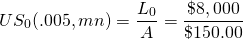
Resolvemos la ecuación usando la función NPER de Excel que se muestra en la Tabla 16.6. La respuesta que se muestra es 62.19 lo que significa que se requerirán 62 pagos regulares y un pago parcial para retirar un préstamo de $8,000 si la tasa de interés APR que se cobra sobre el préstamo es del 6%.
Cuadro 16.6. Encontrar el
número de pagos requeridos para retirar un préstamo
Abrir tabla 16.6 en Microsoft Excel
| B8 | Función: | =NPER (B3/B4, B6, B7, ,0) | |
| A | B | C | |
| 1 | Encontrar el número de pagos requeridos para retirar un préstamo | ||
| 2 | |||
| 3 | tasa | 0.06 | |
| 4 | m | 12 | |
| 5 | n | ||
| 6 | pmt | -150 | |
| 7 | PV | $8,000.00 | |
| 8 | nper | 62.18593 | “=NPER (tasa/m, pmt, PV, ,0) |
Comparación de intereses pagados, plazo de préstamo y montos de pago para préstamos de pago constante
Existe una relación importante entre el plazo del préstamo y el total de intereses pagados. Para ilustrar, considere un préstamo de $30,000 a 15% APR para ser reembolsado en pagos mensuales a lo largo de 30 años. El pago mensual de este préstamo es de $379.33. El interés total TI pagado en un préstamo de pago constante se encuentra multiplicando el pago constante del préstamo A por el plazo del préstamo mn, menos el monto del préstamo L 0:
(16.13)
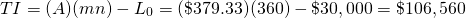
En este caso, el interés total pagado es de $106,560.
Aumentar el monto del pago en 10% a $417.27 reduce el plazo del préstamo en 48% a poco más de 15.36 años (verificar los resultados anteriores usando Excel). En tanto, el interés total pagado se reduce 56% a 46,961 dólares.
La reducción de plazo en respuesta a un aumento en el pago del préstamo no siempre es tan significativa. Por ejemplo, si el préstamo anterior tuviera una TAE del 8%, el pago mensual equivaldría a $220.13 en lugar de $379.22. Incrementar el pago en 10% disminuiría el plazo del préstamo solo 27% de 30 años a 21.93 años, y el interés total pagado disminuiría 32% de $49,247 a $33,722.
Sería útil saber cómo el cambio de plazo del préstamo afecta el tamaño del pago y los intereses totales pagados. Se puede demostrar que a medida que el mn se hace grande, el pago A se acerca al costo de interés por periodo, es decir, el pago más pequeño posible equivale a los intereses cobrados sobre el saldo pendiente del préstamo. Si el prestatario deseara minimizar su pago, el plazo apropiado es el que le permita devolver únicamente los intereses. El plazo de amortización más corto, por otro lado, es uno. Obviamente, existe una compensación entre el tamaño del pago del préstamo y la duración del préstamo.
La elasticidad puntual de plazo, medida en años n con respecto al pago A, mide el cambio porcentual en el plazo n en respuesta a un cambio de 1% en el pago del préstamo. El término elasticidad, E (n, A), se ha calculado como:
(16.14)
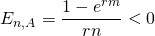
Por ejemplo, un préstamo a 30 años y una TAE del 15% tendrían una elasticidad de plazo igual a:
(16.15)
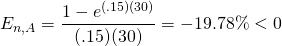
Es decir, aumentar el pago en 1% disminuiría el plazo aproximadamente 19.78%. En contraste, la elasticidad de arco, más que la elasticidad puntual, compara el cambio porcentual en el plazo del préstamo con un incremento del 10% en el pago del préstamo y encuentra que el cambio porcentual en el plazo equivale a 48%, o una elasticidad de arco de plazo igual a 4.8%. Tenga en cuenta que una elasticidad puntual de 19.78% versus una elasticidad de arco de 48% es el resultado de comparar grandes cambios en los pagos de préstamos de 10% versus comparar pequeños cambios en los pagos de préstamos (por ejemplo, .00001%). Consulte el Cuadro 16.7 de elasticidades puntuales a continuación.
Cuadro 16.7. Medidas de elasticidad puntual para préstamos de términos alternativos y tasas de interés.
| n/r % | 1% | 5% | 7.5% | 10% | 15% | 20% |
| 1 | 1.01 | 1.03 | 1.04 | 1.05 | 1.08 | 1.11 |
| 5 | 1.08 | 1.14 | 1.21 | 1.30 | 1.49 | 1.72 |
| 10 | 1.17 | 1.30 | 1.49 | 1.72 | 2.32 | 3.19 |
| 15 | 1.26 | 1.49 | 1.85 | 2.32 | 3.77 | 6.36 |
| 20 | 1.37 | 1.72 | 2.32 | 3.19 | 6.36 | 13.40 |
| 25 | 1.49 | 1.99 | 2.94 | 4.47 | 11.07 | 29.48 |
| 30 | 1.49 | 2.32 | 3.77 | 6.36 | 19.78 | 67.07 |
| 60 | 2.99 | 6.36 | 19.78 | 67.07 | 900.23 | 13,563.00 |
Ejemplo 16.4. Trade-Offs de Pago a Plazo y Préstamo. Lucy Arrendador está financiando la renovación de una propiedad. Necesita un préstamo por 28,000 dólares. Su prestamista le ofrece un préstamo por 20 años a la tasa de interés actual del 15%. Ella calcula que su pago anual es de $4,473.32. Si aumenta su pago en 1% a $4,518.05, su plazo se reduce a 19 años, o una reducción del 5%. Esta reducción porcentual es casi igual al valor tabulado de 6.36 en el Cuadro 16.1, que se encuentra en la intersección de la fila etiquetada 20 y la columna etiquetada 0.15. Los grandes incrementos porcentuales en A, como el 10%, pueden no reflejarse con precisión en la tabla de elasticidades puntuales. Esto se debe a que los cambios porcentuales en n con respecto a A son grandes en comparación con los cambios muy pequeños en n con respecto a A utilizados para calcular la tabla.
Creación de una Tabla de Amortización para Préstamos de Pago Constante
La palabra “amortizar” originalmente significaba “matar”. Así, cuando amortizamos un préstamo, lo matamos o lo extinguimos haciendo pagos regulares, matando el préstamo si se quiere. Una característica del préstamo de pago constante es que, si bien el pago del préstamo es constante, el monto del pago dedicado al pago del préstamo, la parte principal del pago, y el monto del pago dedicado al pago de los intereses del préstamo cambian constantemente. A medida que el principal del préstamo se reduce o se extingue, se reduce el monto del pago dedicado a los cargos por intereses y se incrementa el monto del pago dedicado a reducir el préstamo. Las instituciones de crédito, cuando se les solicite, proporcionarán tablas de amortización que detallen el monto de los intereses y el principal pagado en cada pago durante la vigencia del préstamo. Afortunadamente, Excel nos proporciona las herramientas necesarias para crear nuestras propias tablas de amortización.
Encontrar la parte principal del t th pago del préstamo usando Excel. La función Excel PPMT se puede utilizar para encontrar la parte principal del t th pago del préstamo. La función se expresa como:
(16.16)
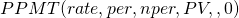
Para ilustrar la función PPMT, considere en $25,000 préstamo para ser reembolsado en cuotas mensuales por cuatro años. La TAE para el préstamo es del 5%. Queremos saber qué parte del 5º pago (periodo) se aplicará al capital del préstamo. La solución Excel se representa en la Tabla 16.8.
Cuadro 16.8. Encontrar el
Principal de Préstamo Pagado en el t º Pago
Abrir Tabla 16.8 en Microsoft Excel
| B8 | Función: | =PPMT (B3/B4, B6, B4*B5, B7, ,0) | |
| A | B | C | |
| 1 | Encontrar el principal del préstamo pagado en el t th pago | ||
| 2 | |||
| 3 | tasa | 0.05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | periodo | 5 | |
| 7 | PV | $25,000 | |
| 8 | Principal pagado | (479.47$) | “=PPMT (tasa/m, periodo, m*n, PV, ,0) |
Resulta que $479.47 del 5to pago se aplican al principal pendiente del préstamo. Además, los estudiantes podrán verificar que la porción principal del 25º pago sea de 521.05 dólares. Esto se debe a que el principal pendiente sobre el que se cobran intereses disminuye a lo largo de la vida del préstamo. A medida que los intereses disminuyen, se puede aplicar una mayor parte del pago del préstamo al principal pendiente del préstamo.
Encontrar el pago de intereses IP (t) sobre el t th pago del préstamo usando Excel. La función Excel IPMT se puede utilizar para encontrar la porción de interés de un pago de préstamo en el t º período y se expresa como:
(16.17)
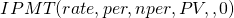
Para ilustrar la función IPMT, volvemos al ejemplo anterior: un monto de préstamo de $25,000, un plazo de 48 pagos mensuales, al 5% TAE, y un deseo de encontrar los intereses pagados en el 5to pago del préstamo. Ilustramos la solución Excel para encontrar intereses pagados en el t º periodo. La solución se ingresa en la celda B8 como $54.68. En el Cuadro 16.9 se describe la solución con más detalle.
Cuadro 16.9. Encontrar los
Intereses de Préstamo Pagados sobre el t º Pago
Abrir Tabla 16.9 en Microsoft Excel.
| B8 | Función: | =IPMT (B3/B4, B6, B4*B5, B7, ,0) | |
| A | B | C | |
| 1 | Encontrar los intereses de préstamo pagados sobre el t th pago | ||
| 2 | |||
| 3 | tasa | 0.05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | periodo | 5 | |
| 7 | PV | $25,000 | |
| 8 | Intereses pagados | ($96.26) | “=IPMT (tasa/m, periodo, m*n, PV, ,0) |
En conjunto, el pago de intereses de $96.26 y el pago principal de $479.47 equivale al pago constante del préstamo de $575.73.
PVs de Préstamos Especiales
Los préstamos y el crédito (capacidad de endeudamiento) hacen posible una economía moderna y firmas exitosas. En ocasiones, los vendedores ofrecen acuerdos especiales de préstamo para alentar a los compradores potenciales a comprar sus productos. Estos pueden incluir préstamos con tasas de interés concesionarias, préstamos de omisión de pago, préstamos de pago por omisión de capital, préstamos de tasa de interés variable y préstamos de pago global. Otras veces las empresas pueden querer ampliar su base de inversión y necesitar refinanciar sus préstamos, o las disminuciones en las tasas de interés pueden proporcionarles un incentivo para refinanciar. Afortunadamente, todos estos préstamos especiales se pueden analizar utilizando modelos fotovoltaicos desarrollados anteriormente. Consideramos los beneficios y costos de varios préstamos especiales en lo que sigue.
Préstamos concesionarios a tasas de interés. Supongamos que la TIR = r de Jane Doe es 10%. Recordemos que una TIR es el costo de oportunidad del defensor y es la tasa adecuada a utilizar al descontar el flujo de caja de inversión. Jane está considerando un préstamo de inversión por $50,000 para ser reembolsado en cuotas mensuales a lo largo de 15 años (mn = 180). La TAE para el préstamo es de 7%, mientras que la tasa actuarial es de 7%/12 = .58%.
Para encontrar el VAN de Jane para este préstamo, primero determinamos el pago de su préstamo A. Esto lo podemos hacer usando la función de Excel PMT (rate, nper, PV, ,0) = PMT (.58,180, $50,000, ,0). El pago A para este préstamo es de: $449.41.
El siguiente paso es tratar el pago del préstamo como un flujo de caja en un problema de inversión y descontar los pagos utilizando la TIR = r del prestatario del 10%, o la tasa de costo de oportunidad actuarial del prestatario de 10% /12= .83%. Usando la ecuación\ ref {16.3}, encontramos:
(16.18)
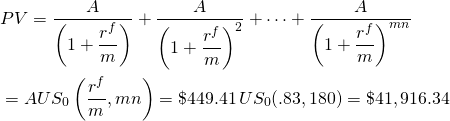
Alguna interpretación de los resultados anteriores puede ser útil. El primer dato importante es que la TIR del prestatario (r = 10%) fue mayor que la tasa de interés del préstamo (r f = 7%). Por lo tanto, el prestatario puede pedir prestado a una tasa inferior a la que ganará invirtiendo el préstamo. El costo real del préstamo del prestatario, lo que se devuelve después de ajustar por lo que gana el préstamo como inversión, es de 41 916.34 dólares, no 50 mil. Otra forma de expresar este resultado es que el valor presente del préstamo fue de 41.916.34 dólares. El Valor Actual Neto (VAN) del préstamo de $50,000 es:
(16.19)
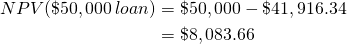
Es decir, el prestatario recibió en forma de préstamo 50.000 dólares en dólares de valor presente. Lo que el prestatario pagó en dólares de valor actual fue de $41,916.34. La diferencia, el NPV, fue de $8,083.66.
Refinanciamiento de un Préstamo de Pago Constante. Una transacción financiera común es la refinanciación de un préstamo de pago constante. Lo que complica esta transacción son los costos de cierre del préstamo o puntos cobrados como porcentaje del préstamo requerido para cerrar. Si la tasa de interés actual es menor que la tasa de interés de uno sobre el préstamo existente, un prestatario razonable preferiría refinanciar. ¿Y si la refinanciación requiere una comisión, puntos porcentuales cobrados como porcentaje del nuevo préstamo, a pagar al cierre del préstamo? Queremos saber lo que el prestatario puede permitirse pagar como costo de refinanciamiento, o puntos del préstamo para alcanzar el punto de equilibrio. Encontrar puntos de equilibrio es lo que hacemos a continuación. Utilizaremos como nuestro punto de partida los números introducidos en el ejemplo anterior.
El problema de la refinanciación es claramente un problema de VPN. Su solución requiere que identifiquemos cuál es el defensor y cuál es la inversión desafiante. El defensor en este caso es el préstamo que ahora tiene el prestatario. El retador es el nuevo préstamo con su tasa de interés reducida y puntos cargados para cerrar el préstamo. Lo que ganará el prestatario con el préstamo no es relevante aquí porque suponemos que esas ganancias serán las mismas independientemente de que se financien con el nuevo préstamo o se sigan financiando con el antiguo préstamo.
Para resolver este problema, reconocemos que si el PV de los pagos de préstamo sobre el nuevo préstamo más puntos cargados para cerrar el préstamo es el mismo que el PV de los pagos del préstamo sobre el préstamo anterior (e ignorando impuestos), los puntos cobrados son de equilibrio. Entonces, usando la ecuación\ ref {16.8}, encontramos puntos de equilibrio cargados para refinanciar como:
(16.20a)
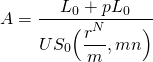
donde pL 0 es el costo que paga el prestatario para refinanciar el préstamo, p por ciento del nuevo préstamo debe pagarse como costo de refinanciamiento, y r N es la tasa de interés del nuevo préstamo. El pago del préstamo sobre el préstamo anterior es:
(16.20b)
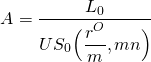
donde r O es la tasa de interés del préstamo antiguo u original. Finalmente, equiparando la ecuación (16.20a) a (16.20b) y resolviendo para p, encontramos los puntos de equilibrio para refinanciar el préstamo; es decir, encontramos el porcentaje del préstamo p que el prestatario podría pagar como cargo de refinanciamiento para obtener un préstamo con una tasa de interés menor y aún así el punto de equilibrio. La fórmula para p es:
(16.21)
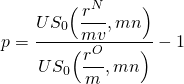
Para ilustrar, vamos r O = 8%, r N = 6%, y dejar mn = 180. Primero resolvemos para p usando Excel:
(16.22)
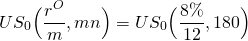
por clavar en PV (tasa, nper, PMT, ,0) = PV (.66,180,1, ,0) y encuentre:
(16.23)
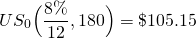
Seguimos los mismos procedimientos para encontrar:
(16.24)
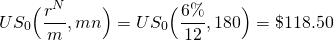
Finalmente, encontramos p haciendo las sustituciones apropiadas en la Ecuación\ ref {16.21}:
(16.25)
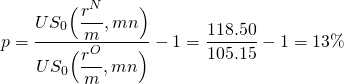
Una variación del problema sería la siguiente: Supongamos que sabíamos qué puntos se cobrarían para refinanciar el préstamo, y queríamos saber qué TAE se requeriría para ser indiferentes entre el nuevo y el viejo préstamo. Es decir, queremos encontrar el punto de equilibrio r N dado que conocemos p, los puntos cobrados para refinanciar el préstamo. La solución se encuentra reordenando la Ecuación\ ref {16.9} de manera que:
(16.26)
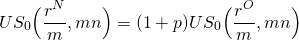
Para ilustrar, supongamos que se sabe que p es del 10%, y las condiciones adjuntas al antiguo préstamo son como antes, de manera que:
(16.27)
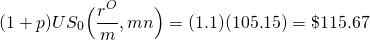
Para encontrar la APR de equilibrio del nuevo préstamo equiparamos:
(16.28)
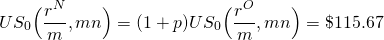
Ahora resolvemos este problema usando la función Excel RATE:
(16.29)
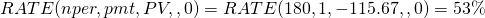
Se muestra la tasa actuarial de equilibrio, .53, que al multiplicarse por 12 equivale a la tasa de préstamo de equilibrio de 6.38%. En comparación con nuestros resultados anteriores, si los puntos pagados para refinanciar el préstamo se redujeran de 13% a 10%, el prestatario podría darse el lujo de pagar 6.38% del nuevo préstamo y aún así alcanzar el equilibrio.
Considera otro ejemplo con p = 15% en el ejemplo anterior. Primera equiparación:
(16.30)
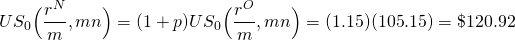
Para encontrar la tasa de interés correspondiente para US 0 (r N /12, 180) = $120.92, ingresamos en la función TASA de Excel:
(16.31)
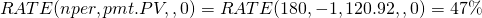
La respuesta que se muestra es: .47 que, al multiplicarse por 12, equivale a la tasa de préstamo de equilibrio de 5.69%. Antes, una nueva tasa de interés de r N = 6% correspondía a puntos de equilibrio de 13%. Si los puntos cobrados fueran 15% en lugar de 13%, la nueva tasa de interés tendría que ser igual a 5.69% para ser indiferente entre continuar con el antiguo préstamo versus pagar los costos de cierre y sacar un nuevo préstamo.
Problemas prácticos de refinanciamiento que enfrentan las empresas agrícolas. Las empresas agrícolas en particular enfrentan variabilidad en los recibos de efectivo. Esto significa que las medidas de liquidez de la empresa, como la relación actual (CT) o la relación tiempo-interés ganado (TIE), también pueden enfrentar una variabilidad significativa con el tiempo, lo que hace que los pagos hipotecarios sean problemáticos. Y en ocasiones, la hipoteca original para una inversión se escribía por un periodo mucho más corto que la vida productiva de la inversión. Cualquiera que sea el caso, las preocupaciones de liquidez pueden requerir que la firma renegocie los términos de sus préstamos con sus prestamistas. Para ilustrar, considere el pago calculado en el Ejemplo 16.2. En este caso se encontró que el pago requerido era igual a $111.22. Supongamos que el prestamista estuviera dispuesto a incrementar el plazo del préstamo en 12 pagos mensuales. ¿Cuál sería el nuevo pago del préstamo? Resolver la función Excel PMT devuelve:
(16.32)
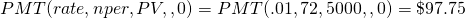
La solución es el pago del préstamo que retirará un préstamo de $5,000 con 72 pagos en lugar de 60 pagos a una tasa actuarial del 1%. El pago del préstamo se reduce de $111.22 a $97.75.
Tasas de interés disfrazadas y tasas de interés efectivas
Uno de los desafíos que enfrentan los gerentes financieros al considerar las decisiones de endeudamiento es conocer el costo real del préstamo, o, dicho de otra manera, conocer la tasa de interés efectiva de la APR. En ocasiones los prestamistas ofrecen préstamos diseñados para disfrazar el costo real de sus préstamos. Llamamos a sus préstamos préstamos a tasa de interés disfrazados. Los préstamos con tasas de interés disfrazadas tienen tasas de interés efectivas aumentadas por métodos distintos de aumentar la tasa de interés del préstamo. Por ejemplo, los costos por intereses pueden restarse en el periodo inicial, reduciendo el monto real del préstamo recibido por el prestatario (un préstamo de descuento). Los intereses se pueden cobrar como si el saldo original del préstamo estuviera pendiente durante toda la vida del préstamo (un préstamo complementario). Alternativamente, el prestamista puede cobrar una comisión por cierre de préstamo, reduciendo el saldo real del préstamo recibido por el prestatario. Además, los intereses pueden agravarse con más frecuencia que los pagos de préstamos. Cada uno de estos métodos aumentará la tasa de interés efectiva por encima de la tasa de interés establecida. Considera varios tipos de préstamos a tasa de interés disfrazados.
El préstamo de descuento: Un prestatario se acerca a su prestamista para obtener un préstamo de L 0 por períodos mn. El prestatario se entera de que la tasa de interés declarada o la tasa de interés encubierta es r d. Cuando el prestatario recoge el cheque de su préstamo, la cantidad que recibe equivale solo a:
(16.33)
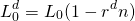
el monto del préstamo solicitado menos la tasa de interés establecida multiplicada por el plazo del préstamo. En tanto, el pago constante del préstamo se calcula como:
(16.34)
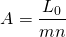
Para calcular la TAE asociada a este préstamo, tratar los pagos del monto A como si estuvieran asociados a un préstamo de pago constante que retire un monto principal de L d. La relación se expresa como:
(16.35)
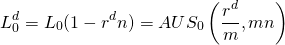
A continuación, sustituyendo por A, L 0 /mn, encontramos:
(16.36)
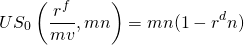
Para ilustrar el préstamo de descuento, suponga que un consumidor obtiene un préstamo a plazos por $10,000, del cual se deducen $2,500 por costos de intereses. El préstamo debe ser reembolsado a lo largo de 2 años, con pagos mensuales iguales a $416.67 = ($10,000/24). Para resolver este ejemplo, primero debemos encontrar la tasa indicada r d:
(16.37)
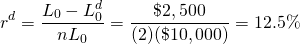
Normalmente, se da la tarifa indicada, pero es recomendable confirmarla como lo hemos hecho anteriormente. Ahora ingresamos nuestros números en la Ecuación\ ref {16.36} y obtenemos:
(16.38)
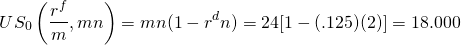
Para encontrar la tasa actuarial, ingresamos a nuestra función TASA Excel:
(16.39)
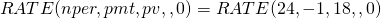
Se muestra la tasa mensual actuarial de 2.44% o, después de multiplicar por 12, encontramos la tasa TAE correspondiente de 29.3%. La tasa efectiva r e es: r e = (1.0244) 12 — 1 = 33.55%.
Esta es una gran diferencia respecto a la tasa de interés declarada de 12.5%. De ahí que el préstamo de descuento disfraza efectivamente su verdadera TAE.
Préstamos con puntos agregados. En ocasiones los prestamistas cobran puntos p para cerrar un préstamo. La comisión tiene el efecto de aumentar la tasa de interés sobre el préstamo ya que el prestamista gana más de lo que sugiere la tasa indicada. La tasa de TAE para dicho préstamo se puede calcular calculando primero el pago que retira el préstamo, más los puntos agregados. El pago es igual a:
(16.40)
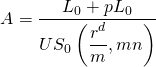
A continuación, exprese la relación entre el pago A en la Ecuación\ ref {16.40}, tasa APR r f, y el monto real del préstamo recibido como:
(16.41)
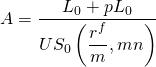
Al igualar las ecuaciones (16.40) y (16.41), encontramos r f a partir de la igualdad:
(16.42)
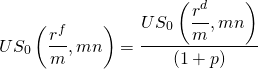
Para ilustrar cómo encontrar la tasa de interés efectiva para un préstamo de puntos agregados, considere el siguiente problema. Un banco ofrece una tasa de préstamo del 12% con pagos mensuales por tres años, con una comisión de cierre de préstamo del 3%. ¿Cuál es la tasa de interés APR r f? Usando la ecuación\ ref {16.42} encontramos primero:
(16.43)
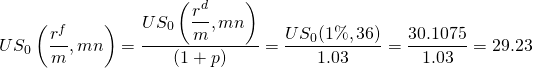
Para encontrar la verdadera tasa actuarial, ingresamos a nuestra función Excel RATE:
(16.44)
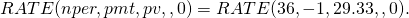
Se muestra la tasa mensual actuarial de 1.15%, o después de multiplicar por 12, encontramos la tasa TAE correspondiente de 13.83%. La tasa efectiva r e es: r e = (1.0115) 12 — 1 = 14.71%. Esto es bastante diferente en comparación con la tasa de interés declarada del 12%.
Resumen y Conclusiones
En este capítulo demostramos la versatilidad de los modelos fotovoltaicos utilizándolos para analizar préstamos. Para préstamos de pago constante, utilizamos modelos fotovoltaicos para resolver pagos constantes de préstamos, términos, montos de préstamos y tasas de interés, recordando que una ecuación PV puede resolver como máximo una desconocida.
El uso de modelos fotovoltaicos para analizar los préstamos requirió identificar los distintos tipos de tasas de interés. Este fue un ejercicio importante porque descubrimos la diferencia entre las tasas de interés declaradas y las tasas de interés efectivas, la tasa de interés realmente pagada sobre los fondos del préstamo puestos a disposición.
Otro ejercicio importante fue descubrir la sensibilidad de la relación entre el tamaño del pago del préstamo y el plazo del préstamo. En la mayoría de los casos, la relación no es uno a uno. En otras palabras, un incremento del 1% en el tamaño del pago del préstamo rara vez lleva a una caída de 1% en el plazo. El descenso porcentual correspondiente en el plazo del préstamo suele ser mucho, mucho más. De ahí que descubrimos que, al solicitar préstamos, vale la pena explorar varios términos y tamaños de pagos de préstamos y encontrar la mejor combinación, la que tenga el equilibrio óptimo entre plazo y liquidez.
Un problema común es que los préstamos existentes a menudo necesitan ser refinanciados. Tal puede ser el caso cuando bajan las tasas de interés o se amplía un proyecto actualmente financiado y se requieren fondos adicionales. En el texto consideramos refinanciar préstamos existentes y encontramos puntos de cierre de préstamos de equilibrio. En los materiales suplementarios al final de este capítulo, encontraremos la fórmula más general para refinanciar cuando el plazo, la tasa de interés y el tamaño del nuevo préstamo puedan ser diferentes a los del préstamo existente.
Por último, demostramos cómo algunos préstamos pueden disfrazar la verdadera tasa de interés. Si bien solo ilustramos la solución para el préstamo de descuento y el préstamo de puntos agregados, hay varios otros tipos de préstamos que disfrazan la verdadera tasa de interés.
Preguntas
- ¿Cuál preferirías ganar con tus ahorros? ¿Una tasa de TAE de 12.5% o una tasa actuarial de 1% agravada mensualmente? Ante una TAE de r por ciento, ¿qué es lo más que puede ganar la tasa efectiva por encima de la tasa APR si se compone continuamente?
- Considera un préstamo de $80,000 a una APR de 13%. ¿Cuál es el pago del préstamo que retiraría el préstamo si se reembolsa en pagos mensuales por 10 años? ¿Si se reembolsa en cuotas mensuales por 9 años? Comparar el cambio porcentual en el plazo frente al cambio porcentual en el pago del préstamo (la elasticidad del arco). Finalmente, encuentra la elasticidad puntual E (n, A) en el préstamo original.
- Asumir un préstamo de $54.000 con un plazo restante de 21 años. El préstamo existente requiere pagos mensuales a una APR de 11.25%. Por una comisión de cierre del 3%, los prestatarios podrían refinanciar su préstamo a una tasa APR del 10% para el mismo plazo. ¿Cuál es la tasa de interés efectiva del nuevo préstamo? ¿Cuáles son los puntos de equilibrio para refinanciar el préstamo? ¿Cuál es el interés total pagado por los dos préstamos?
- Un consumidor obtiene un préstamo a plazos de $12,000 del cual se deducen $2,700 por costos de intereses. El préstamo debe ser reembolsado a lo largo de dos años con pagos mensuales iguales a $500 ($12,000/24). Por favor, determine la tasa de interés efectiva r e de este préstamo.
- Una tienda de suministros agrícolas ofrece a sus clientes 30 días lo mismo que en efectivo. Es decir, para las facturas pagadas dentro de los 30 días posteriores a la realización de las compras, no se cobran intereses. Por otro lado, para fomentar los pagos anticipados, la tienda de suministros ofrece un 2% de descuento en facturas pagadas con 10 días. Por favor, calcula la tasa de interés efectiva que la tienda ofrece a sus compradores por renunciar a 20 días de crédito gratuito.
- Supongamos que tomó prestados $5,000 por 3 años a una tasa APR del 8%. Crear una tabla de amortización para este préstamo.
- Home Depot envió por correo a algunos de sus clientes un cupón que les daba derecho a un 10% de descuento en su próxima compra o dos años de crédito gratuito. ¿Bajo qué condiciones quedarías indiferente entre las dos opciones? (Pista: la respuesta no depende de la cantidad comprada.)
- Una firma agrícola tiene un préstamo hipotecario por $150,000 a una tasa APR del 5%. El plazo del préstamo es de 15 años y los pagos equivalen a 14.451 dólares. Los problemas de flujo de efectivo por ingresos agrícolas reducidos dejan a la firma solo capaz de pagar $10,000 en este préstamo. ¿A qué equivaldría el nuevo plazo si el prestamista permitiera que el prestatario reembolse a más largo plazo?
Materiales Suplementarios
El problema de refinanciamiento descrito en este capítulo puede ser más
complicado. ¿Y si no solo la tasa de préstamo APR nueva y antigua fueran
diferentes sino también el plazo y la cantidad refinanciada? Que
r O y r N sean iguales a la TAE en
los préstamos antiguos y nuevos respectivamente. Supongamos que el nuevo préstamo
incluyó no sólo el préstamo refinanciado L 0 sino
también un monto adicional igual a L 0.
También supongamos que el plazo sobre el préstamo antiguo es
mn O comparado con el plazo del nuevo préstamo,
mn N. Queremos saber si el prestatario debe
refinanciar. El TIR utilizado para calcular los NPV para los préstamos nuevos y
antiguos es r.
L 0.
También supongamos que el plazo sobre el préstamo antiguo es
mn O comparado con el plazo del nuevo préstamo,
mn N. Queremos saber si el prestatario debe
refinanciar. El TIR utilizado para calcular los NPV para los préstamos nuevos y
antiguos es r.
Recordemos que si la TIR es también la tasa de reinversión, entonces el VPN de una inversión no se ve afectado al cambiar su tamaño y plazo. Por lo tanto, podemos determinar si el prestatario debe refinanciar comparando los NPV del préstamo antiguo y nuevo (refinanciado).
Supongamos por el momento que conocemos los puntos cobrados para refinanciar un préstamo y queremos conocer nuestro pago de préstamo para el préstamo refinanciado. Usando la notación ya definida, resolvemos el problema revisando la ecuación (16.21a) y escribimos la ecuación revisada como:
(16.i)
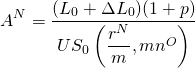
El pago del préstamo para el préstamo original (antiguo), por el que no se cobran puntos, puede escribirse como:
(16.ii)
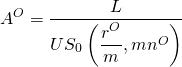
En este punto, hacemos una suposición crítica; es decir, que los fondos se reinvierten en la TIR del defensor, lo que nos permite escribir los NPV para los préstamos nuevos y antiguos como:
(16.iii)
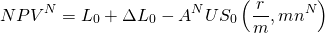
y
(16.iv)
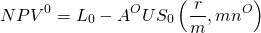
Si los puntos cargados hacen que los dos préstamos sean iguales en VPN, entonces podemos equiparar las ecuaciones (16.iii) y (16.iv) y resolver para los puntos de equilibrio:
(16.v)
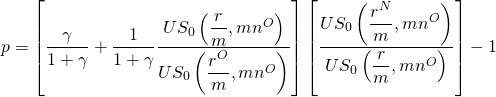
Dónde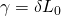 .
Tenga en cuenta que si
.
Tenga en cuenta que si = 0" title="Rended by Quicklatex.com” height="18" width="174"
style="vertical-align: -5px; "> y
n O = n N, la
ecuación (16.v) se reduce a la ecuación\ ref {16.22}. Por lo tanto,
la ecuación (16.v) nos permite encontrar puntos de equilibrio en general,
incluso si las tasas de interés, plazo y tamaño de los préstamos refinanciados
son diferentes en comparación con el préstamo que se refinancia.
= 0" title="Rended by Quicklatex.com” height="18" width="174"
style="vertical-align: -5px; "> y
n O = n N, la
ecuación (16.v) se reduce a la ecuación\ ref {16.22}. Por lo tanto,
la ecuación (16.v) nos permite encontrar puntos de equilibrio en general,
incluso si las tasas de interés, plazo y tamaño de los préstamos refinanciados
son diferentes en comparación con el préstamo que se refinancia.


