4.8: Capítulo 4 Excercises
- Page ID
- 59657
P4.1 (4 puntos)
Muchas aulas están equipadas con proyectores de
video que se pueden conectar a
computadoras portátiles y portátiles para su uso durante las reuniones de clase.
a. En base a su experiencia con tales sistemas, ¿cuál es la
probabilidad de que el sistema de proyección falle en el transcurso
de un año de clases regulares en dicha sala?
b. Desarrollar un árbol de fallas de causas potenciales para un sistema de
proyección de video en el aula.
P4.2 (8 puntos)
A continuación aparecen una serie de resúmenes de condiciones de inspección de techos, donde 1 es excelente y 5 es pobre. Obsérvese que una inspección 1997.5 ocurrió en el segundo semestre de 1997, mientras que 1997 ocurrió en el primer semestre de 1997. El techo fue reemplazado en 1985. Responde las preguntas que aparecen a continuación. Podría usar ayudas de software, como EXCEL o MATLAB, para este problema.
| FECHA | CONDICIÓN |
| 1985 | 1 |
| 1985.5 | 1 |
| 186.5 | 2 |
| 1997 | 2 |
| 1997.5 | 2 |
| 1998 | 2 |
| 1998.5 | 2 |
| 1999 | 3 |
| 1999.5 | 3 |
| 2000 | 4 |
| 2000.5 | 4 |
| 2001 | 4 |
| 2002 | 4 |
| 2002.5 | 4 |
| 2003 | 5 |
a. Estimar un modelo ordinario de deterioro por regresión de mínimos cuadrados de la forma: Condición =\ (a + b (edad)\) donde la edad es la edad del techo en años. Informe sus estimaciones de parámetros, errores estándar, estadísticas t y\(R^2\) valores. ¡Tenga en cuenta que hay una brecha en los datos de 1985 a 1996!
b. Supongamos que tengo un techo comparable que tiene 12 años de antigüedad. ¿Cuál sería su modelo de regresión en (a) predecir para su condición? ¿Qué predeciría para los 18 años? ¿A qué edad se espera que el padecimiento llegue a ser 5?
c. Trazar los datos y su línea de regresión.
d. ¿ Cree que un modelo de regresión no lineal se ajustaría mejor a los datos? Pruebe un modelo cuadrático (Condition =\(a + b(age) + c(age^2)\) y un modelo exponencial (Condition =\(a*age^b\)) y discuta sus resultados. ¿Qué modelo tiene un mejor ajustado\(R^2\)? ¿Qué modelo usarías en la práctica para la predicción de deterioro?
P4.3 (16 puntos)
Formular un sencillo modelo de proceso de Markov de la condición del techo. Supongamos que las transiciones ocurren cada seis meses y pueden ser un retorno a la condición actual o una transición a la siguiente peor condición (a excepción del estado 5 que es un estado absorbente sin salida en este modelo de deterioro...)
a. Dibuja tu modelo de proceso como una serie de estados (en círculos) y posibilidades de transición (como flechas) para cinco estados correspondientes a las condiciones del techo 1 a 5.
b. Supongamos que la probabilidad de permanecer en el estado 1 es de 0.93 en cualquier transición. Estime (a partir de los datos anteriores) o calcule (cuando corresponda) las probabilidades de transición restantes y márquelas en su diagrama de proceso.
c. Desarrollar una matriz de transición de Markov para su proceso.
d. Supongamos que comienzas en el tiempo 0 en el estado 1. Calcula la probabilidad de estar en cada estado durante los próximos veinte años (o 40 transiciones) en función de tu modelo.
e. Supongamos que cree que un techo debe ser reemplazado cuando la condición del techo alcanza el estado 5. Comenzando con un nuevo techo (estado 1 en tiempo 0), trazar la probabilidad de estar en el estado 5 en función del tiempo.
f. Calcula el tiempo de servicio esperado del techo con base en tus datos en la parte e. Puedes suponer que el tiempo de servicio esperado es cuando la probabilidad de ingresar al estado 5 alcanza el 50%.
g. Si ejecutó su modelo hasta el límite (tiempo infinito), ¿cuál es la probabilidad de estar en cada estado?
h. ¿Cómo se compara tu modelo de procesos de Markov con tu modelo de regresión lineal en la Pregunta 1? En particular, ¿es diferente el tiempo de servicio esperado? ¿El modelo de Markov no es lineal? ¿Por qué o por qué no? ¿Cuál es preferible y por qué?
P4.4 (6 puntos)
Supongamos que tengo el
sistema de tuberías simple que se muestra a continuación:
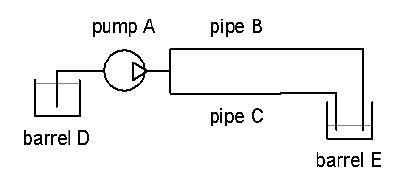
Para este sistema sencillo, desarrollo un árbol de fallas para el análisis de fallas
como:
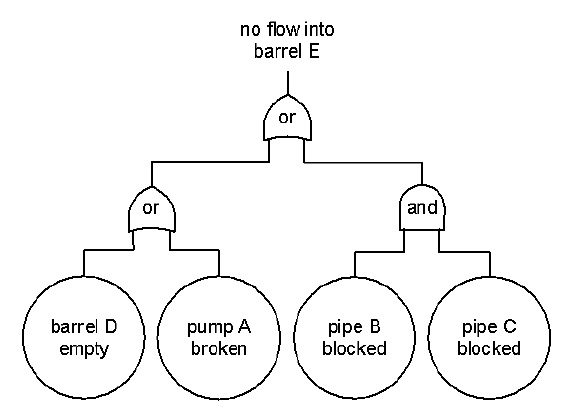
Supongamos además que las probabilidades de falla estimadas de los cuatro subeventos son independientes y son las siguientes (de izquierda a derecha en la figura):
| Evento | D vacío | A roto | B bloqueado | C bloqueado |
| Probabilidad de Evento | 0.15 | 0.05 | 0.1 | 0.1 |
P4.1 (4 puntos)
Muchas aulas están equipadas con proyectores de
video que se pueden conectar a
computadoras portátiles y portátiles para su uso durante las reuniones de clase.
a. En base a su experiencia con tales sistemas, ¿cuál es la
probabilidad de que el sistema de proyección falle en el transcurso
de un año de clases regulares en dicha sala?
b. Desarrollar un árbol de fallas de causas potenciales para un sistema de
proyección de video en el aula.
P4.6 (4 puntos)
Con el crecimiento de los proveedores de servicios de internet, un investigador decide examinar si existe una correlación entre el costo del servicio de internet por mes (redondeado al dólar más cercano) y el grado de satisfacción del cliente (en una escala de 1 - 10 con un 1 no satisfecho en absoluto y un 10 siendo extremadamente satisfecho). El investigador sólo incluye programas con tipos de servicios comparables. A continuación se proporciona una muestra de los datos.
| Dolares | Satisfacción |
| 11 | 6 |
| 19 | 8 |
| 17 | 10 |
| 15 | 4 |
| 9 | 9 |
| 5 | 6 |
| 12 | 3 |
| 19 | 5 |
| 22 | 2 |
| 25 | 10 |
a. Trazar los datos. ¿Crees que los dólares y la satisfacción están relacionados (o correlacionados)?
b. Estimar una regresión lineal con Satisfacción = a + b*dólares. Discuta sus resultados.
P4.7 (3 puntos)
¿Cuáles de las siguientes son matrices de transición para procesos de Markov? Explique.
a.\ begin {bmatrix}
.4 & .3 & .3\\
.2 & .4 & .4\\
.6 & .1 & .3\\
\ end {bmatrix}
b.\ begin {bmatrix}
.2 & .3 & .5\\
.6 & .1 & .2\\
.7 & .1 & .3\\
\ end {bmatrix}
c.\ begin {bmatrix}
.25 & .15 & .3 & .4\\
.5 & 0 & .15 &
.3\\
.15 & .35 & .4 & .2\\
.1 & .5 & .2 & .2\\
\ end {bmatrix}


