Saltar al contenido principal
LibreTexts Español

4.7: Análisis del árbol de fallas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    59682

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    En la sección anterior se describían diversos modelos de previsión de fallas de componentes. Los árboles de fallas se utilizan para pronosticar la probabilidad de falla de un sistema de componentes en función de la probabilidad de fallas de componentes. Los árboles de fallas proporcionan un medio para identificar debilidades en los sistemas y permitir que los gerentes realicen cambios para reducir el riesgo de falla.

    Los árboles de fallas comienzan con un nodo superior que representa la condición de todo el sistema. Las causas de la falla del sistema se deve4loped entonces como una serie de eventos y subcomponentes que pueden causar fallas. Se pueden incluir múltiples capas de subcomponentes. La Figura 4.7.1 ilustra un árbol de fallas simple con tres capas y ocho elementos diferentes.

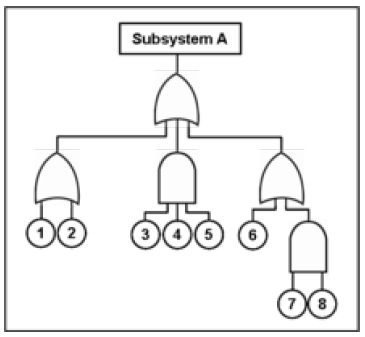    clipboard_e271530f01bf0a5869a34e3ec0df73b73.pngFigura\(\PageIndex{1}\): Ilustración de un árbol de fallas con ocho subcomponentes o eventos diferentes. Fuente: Por Offnfopt, modelado a partir de imagen creada por U.S. Military - Obra propia creada desde cero usando Archivo:Fault tree.png como referencia, Public Domain, https://commons.wikimedia.org/w/inde...curid=52420454.

    Como ejemplo, supongamos que un administrador de infraestructura tiene la tarea de garantizar que la electricidad esté disponible en un edificio en todo momento. El directivo invierte en un generador de respaldo en caso de que falle la electricidad de la red. En este caso, el edificio podría no tener electricidad si falla la red eléctrica y el generador de respaldo no arranca. En un día cualquiera, si hay un 1% de probabilidad (0.01 de probabilidad) de que la red eléctrica pueda fallar y un 5% de probabilidad (0.05 de probabilidad) de que falle los generadores de respaldo, entonces hay una probabilidad de 0.0005 o 0.05% de que la electricidad falle. Este es un ejemplo en el que la redundancia de fuentes de energía reduce las posibilidades de no tener energía para el edificio. Otro paso del análisis podría ser examinar las razones de la falla del generador de respaldo, como la falta de combustible o daños en el cableado. Además, un gerente podría establecer un régimen de inspección regular para que el generador de respaldo intente reducir su probabilidad de falla del 5%.

    Esta provisión de energía eléctrica es un ejemplo de redundancia con un nodo 'y': tanto la red eléctrica como el generador de respaldo deben fallar para que el sistema falle. Desafortunadamente, también pueden ocurrir fallas en el sistema si ocurre cualquiera de una serie de eventos. Esto sería un nodo 'o'. Por ejemplo, una escalera fallaría si alguno de los dos soportes verticales fallara. Si la probabilidad de que falle un soporte vertical es del 1% (0.01 de probabilidad) en el uso normal, entonces la probabilidad de éxito es de 0.99. Existen cuatro casos que podrían derivarse del uso:

    1. Ambos soportes verticales funcionan con probabilidad 0.99*0.99 = 0.9801
    2. El soporte izquierdo se rompe y el soporte derecho no falla, pero la escalera como sistema falla con probabilidad 0.01*0.99 = 0.0099
    3. El soporte derecho se rompe y el soporte izquierdo no falla, pero la escalera como sistema falla con probabilidad 0.01*0.99 = 0.0099
    4. Ambos soportes verticales fallan y el sistema de escalera falla con probabilidad 0.01*0.01 = 0.0001

    Con una relación de nodo 'o' (múltiples causas potenciales de falla), la probabilidad de falla se puede calcular como:

    \[\text { Pr \{ failure } \}=\Sigma_{i}\{1-\mathrm{~ P r ~ ( s u b c o m p o n e n t ~ i ~ f a i l u r e ) \} ~}\]

    Donde la suma\(\Sigma\) se toma sobre todos los subcomponentes incluidos en el nivel de nodo 'o'.

    Una convención común al dibujar redes de árboles de fallas es representar las relaciones de puerta 'o' con una curva en la parte inferior (como en la puerta superior en la figura 4.6.6) y una relación de puerta 'y' con una parte inferior recta (como en la puerta inferior para los eventos 7 y 8 en la figura 4.6.6). La probabilidad de falla del sistema en la Figura 4.6.6 se rastrearía entonces a través de las tres puertas 'o' y las dos puertas 'y':

    \ [\ mathrm {~ P r\ {S y s t e m ~ F i g. ~ 4. x ~ f a i l u r e\} ~} = [1- (1-Prelevent 1 falla)) * (1-Pr [evento 2 falla]] +
    \ texto {Pr\ {evento} 3\ mathrm {~ f a i l u r e\} * P r\ {e v e e t ~} 4\ texto {falla}\}\ texto {'Prievent} 5\ texto {falla}\} +
    \ left [1- (1-\ texto { Prievent} 6\ text {error}\} ^ {*} (1-\ text {Pr fevent} 7\ text {falla}\} ^ {*}\ text {Pr}\ text {[evento} 8\ text {falla}\ derecha]] Eq.\]

    Se pueden definir puertas de relación más complicadas (como puertas 'o' exclusivas), pero no son ampliamente utilizadas para ningún modelo de falla de infraestructura. Estas relaciones más complicadas pueden encontrar utilidad en el análisis del árbol de fallas de circuitos o sistemas operativos de computadora.

    Una complicación en el cálculo de las probabilidades de falla mostradas anteriormente ocurrirá cuando las fallas se correlacionen de alguna manera. Por ejemplo, las inundaciones pueden hacer que tanto la red eléctrica como el generador de respaldo fallen en el ejemplo de energía eléctrica anterior. En este caso, la probabilidad directa de que falle el generador de respaldo, Pr {generador de respaldo de falla} se reemplazaría con la probabilidad de falla del generador de respaldo condicional a la falla de la red eléctrica: Pr {falla generador de respaldo │ falla red eléctrica}. Por supuesto, un administrador de infraestructura prudente podría asegurar que el generador de respaldo esté protegido de inundaciones, por lo que esta posibilidad de falla del sistema por inundación desaparecería.

    Otra dificultad para el análisis del árbol de fallas para la infraestructura es que algunos sistemas pueden no fallar completamente, pero pueden degradar en rendimiento. Por ejemplo, un techo puede comenzar a gotear en lugar de fallar por completo. Para tales casos, se pueden definir estados de degradación separados y desarrollar árboles de fallas para cada nivel de degradación.

    El análisis del árbol de fallas requiere bastante mano de obra y es difícil ser exhaustivo sobre los posibles modos de falla. Sin embargo, el proceso conceptual de identificación de causas y eventos de fallas puede ser útil para administrar la confiabilidad de los sistemas de infraestructura.

    This page titled 4.7: Análisis del árbol de fallas is shared under a CC BY-SA license and was authored, remixed, and/or curated by Donald Coffelt and Chris Hendrickson.