5.3: Optimización de enteros para la administración de infraestructura
- Page ID
- 59936
En muchos problemas de optimización de administración de infraestructura, las variables de decisión pueden restringirse a valores enteros. Por ejemplo, en el apartado anterior, las variables de decisión se definieron como emprender una acción particular de mantenimiento o rehabilitación j en un segmento de calzada i. Si bien la variable de decisión podría ser una fracción, por lo que sólo una parte del segmento vial se somete a una actividad de mantenimiento, es más natural para gestionar el segmento como un todo y desear tener variables de decisión binarias que sean cero o una.
Las restricciones enteras imponen varios problemas en la obtención de soluciones óptimas. Para la programación lineal, se podrían buscar valores óptimos en las esquinas extremas de la región factible. Con restricciones de valor entero, la solución óptima puede estar dentro de la región factible. Como se ilustra en la Figura 5.3.1, los valores enteros factibles se muestran como puntos dentro de una región que satisface las restricciones lineales. La única solución factible en una esquina extrema sería la solución\(x1 = 0\) y\(x2 = 0\). El punto A marcado en la figura tendría valores fraccionarios de\(x1\) y\(x2\).
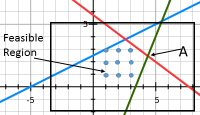
Un enfoque para la programación de enteros es ignorar las restricciones de enteros y resolver el problema como un programa lineal. Con restricciones binarias y parámetros enteros y valores de restricción, este enfoque trabaja frecuentemente para dar soluciones binarias óptimas. Un valor de variable de decisión fraccional puede ser redondeado por un gerente para obtener una solución muy buena pero no necesariamente estrictamente óptima en este enfoque. Dada la incertidumbre en costos y efectos de acción, el redondeo podría no afectar el desempeño general de la infraestructura.
También existen métodos más formales para obtener soluciones óptimas de enteros. Un enfoque popular es “ramificar y encuadernar”. En este proceso, se obtiene una solución lineal inicial, y luego se agregan restricciones para obligar a la solución a ser un número entero. Por ejemplo, en la Figura 5.3.1, si se obtuvo el punto A como la solución óptima, y una buena restricción adicional podría\(x1\) ser requerir ser 3 o menos:\(x1 \leq 3\). Esta sería una nueva 'rama' para la solución del problema con un 'bound' que corta una porción de la región que no contiene valores enteros. Agregar restricciones de esta manera continuaría hasta que se obtenga una solución óptima de valor entero.
'Branch and bound' u otros enfoques de programación de enteros son parte del software de optimización más popular, incluido el programa Solver para la hoja de cálculo EXCEL. Las restricciones de número entero se especifican cuando se introduzcan problemas en los programas. Sin embargo, la resolución de programas enteros requiere más tiempo de cálculo que los programas lineales de tamaño comparable. Si bien los programas lineales con miles de variables de decisión se pueden resolver fácilmente, los programas enteros pueden limitarse de manera realista a cientos de variables de decisión. Aún así, esto bien podría ser un rango útil para muchos problemas de gestión de infraestructura.
El problema del 'vendedor viajante' es un ejemplo clásico de un problema de programación de enteros. El problema es desarrollar un recorrido de ida y vuelta que visite todas y cada una de las ciudades exactamente una vez con una distancia mínima de viaje. Para la administración de infraestructura, un recorrido de este tipo puede ser formulado por un inspector de diferentes componentes de infraestructura o un trabajador de mantenimiento con un conjunto de trabajos asignados. En estos problemas, las 'ciudades' serían lugares de inspección o de trabajo. El software de enrutamiento UPS para camiones de reparto mencionado en la introducción a este capítulo resuelve este problema (UPS 2016). Las variaciones del problema se pueden encontrar en la manufactura (donde las 'ciudades' pueden ser manchas en un chip) y la secuenciación del ADN.
Una variable de decisión para el problema del vendedor ambulante podría ser \(x_{ij}\) que es 0 si el viaje de\(i\) a no\(j\) está en el recorrido y 1 si el viaje de\(i\) a\(j\) está en el recorrido. La función objetiva sería sumar la distancia (o costo) del viaje de\(i\) a\(j\) multiplicado por los\(x_{ij}\) valores. Solo aquellos viajes que forman parte del recorrido incurrirían en alguna distancia y afectarían el valor de la función objetiva. Las restricciones requieren que haya exactamente una salida de cada ciudad (por lo que la suma de la\(x_{ij}\) de I equivale a una) y exactamente una llegada a cada ciudad. Se necesitan restricciones adicionales para garantizar que el recorrido esté completo (es decir, el recorrido no tiene múltiples circuitos disjuntos). Finalmente, las variables de decisión \(x_{ij}\) están restringidas a cero o a uno.
Se han desarrollado numerosos algoritmos especializados para el problema del vendedor ambulante. En la práctica, los enfoques heurísticos pueden obtener soluciones muy buenas (pero no necesariamente óptimas).


