5.2: Optimización Lineal para Administración de Infraestructura

Los problemas con las variables de decisión continua y las restricciones lineales y las funciones objetivas son muy comunes y han atraído considerable atención de la investigación. Estos problemas se resuelven con algoritmos de programación lineal como el método Simplex. El software típico puede acomodar miles de variables de decisión y restricciones.

Formalmente, un programa lineal se representa como:

\[ \text{Maximize c} * \text{x subject to A x} =\text{y and x} \geq 0 \]

Donde c es un vector de parámetros, x es un vector de variables de decisión continua, A es una matriz de parámetros e y es un vector de parámetros de restricción. Esta formulación puede acomodar restricciones de desigualdad con la adición de variables de decisión que representan holgura en las restricciones. Por ejemplo, la restricción\(x1 + x2 ≤ 5\) (mostrada en la Figura 5.2.1) se reescribiría como\(x1 + x2 + x3 = 5 \) y un valor positivo de x3 en la solución óptima indicaría que la restricción no es vinculante. De igual manera, las variables de decisión pueden tomar cualquier valor (tanto negativo como positivo) con la adición de variables de decisión. En la práctica, el software de programación lineal puede tomar como entrada desigualdades y variables de decisión sin restricciones y convertir el problema en la forma estándar de la Ec. 5.2.1.

Un programa lineal tiene tres tipos de posibilidades de solución:

• Ninguna solución es posible. Un ejemplo sería: Maximizar variable de decisión x sujeta a las restricciones x < 1 and x > 5. Ningún valor de x satisfará ambas restricciones. Para la gestión de infraestructura, un ejemplo sería si un presupuesto es inadecuado para lograr las condiciones funcionales requeridas.
• Existe una única solución óptima. Por ejemplo, un problema de gestión de carreteras podría ser maximizar la condición promedio de los segmentos de calzada sujetos a una restricción presupuestaria. Por lo general, se identificará un conjunto de acciones de mantenimiento (como repavimentación o parcheo) para un subconjunto de segmentos de carreteras que utilicen completamente el presupuesto. A continuación aparece un ejemplo más extenso de este problema.

Existen múltiples soluciones óptimas. En la Figura 5.2.1, el segmento de línea entre A y B incluye un número infinito de soluciones óptimas que son combinaciones de las dos variables de decisión x1 y x2 para el programa lineal Maximizar\( 2 * x1 + x2 \text { subject to } 2 * x1+x 2 \leq 4 \text {and } x 1, x 2 \text { both} \geq 0\). La región factible es el área triangular ABO.

Figura\(\PageIndex{1}\): Ilustración de Múltiples Soluciones Óptimas.

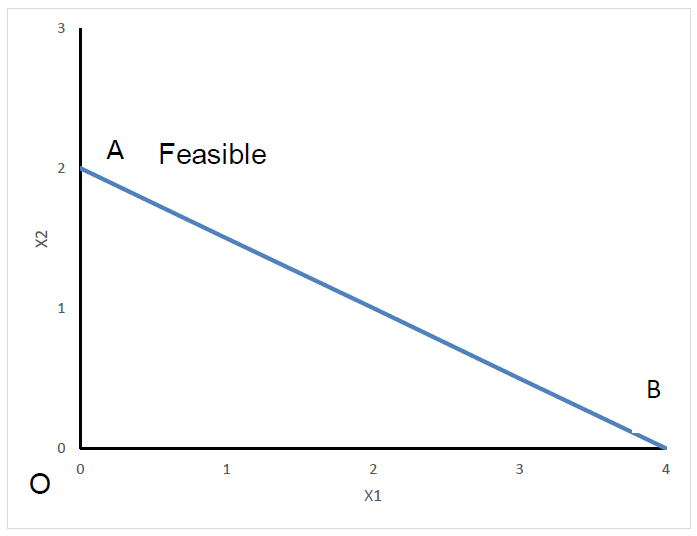
Los programas lineales poseen la propiedad útil de que el conjunto de soluciones factibles forman una región convexa. “Factible” en este contexto significa una combinación de variables de decisión que satisfacen las limitaciones del problema. El área sombreada en la Figura 5.2.1 es la región factible para x1 y x2. El área sombreada es convexa porque el segmento de línea entre dos combinaciones factibles cualquiera de x1 y x2 aún estaría en la región factible. Esta convexidad tiene dos implicaciones útiles. En primer lugar, cualquier solución óptima no será una óptima local sino que sería una óptima global. Es decir, si encuentras una combinación de x1 y x2 para la cual no es posible ninguna mejora a partir de pequeños cambios, entonces ninguna otra combinación de x1 y x2 con ser mejor. En segundo lugar, los valores óptimos de las variables de decisión para un problema de programa lineal se ubicarán en el límite de la región factible, como el segmento de línea en la Figura 5.2.1. Esta propiedad es utilizada por el algoritmo de solución Simplex para programas lineales.

El método Simplex es un método de solución común para problemas de programación lineal. Comienza con una 'solución básica factible'. Con m restricciones y n variables de decisión, una solución básica factible consiste en n-m variables de decisión establecidas en cero y las restantes m variables de decisión la solución a las ecuaciones de restricción lineal m. El método simplex verifica si la mejora es posible intercambiando una de las variables de decisión n-m establecidas en cero con una variable de decisión en la solución básica factible. Si la mejora es posible, el algoritmo realiza este cambio, lo que equivale a 'pivotar' de un punto extremo en la región convexa factible a otro. Los pivotes continúan hasta que no sea posible tal mejora. Una solución inicial básica factible se puede obtener simplemente agregando 'variables de decisión artificiales' iguales al valor de los parámetros de restricción y luego pivotando lejos de estas variables artificiales.

El mantenimiento y rehabilitación de carreteras es un buen ejemplo de programación lineal aplicada a la gestión de infraestructura. En esta aplicación, una red de carreteras se divide en numerosos tramos cortos que pueden variar desde unos pocos kilómetros hasta bloques individuales en una red urbana (con índice I que va de 1 a n segmentos). Se definen posibles acciones de mantenimiento para los tramos de calzada, como llenar baches (j = 1), repavado (j = 2) o no hacer nada (j = 3). Luego se estiman los costos de cada acción para cada sección de pavimento, generalmente con base en el área de la sección de pavimento (\(p_{ij}\)). El estado de cada tramo de pavimento se pronostica asumiendo que se realiza una acción (rellenar baches, repavimentar o no hacer nada en este ejemplo) (\(c_{ij}\)donde valores menores de\(c_{ij}\) son más deseables). Luego se define una restricción presupuestal para acciones y una función objetiva (como maximizar la condición promedio del sistema). El resultado es un problema de programación lineal:

\[ \text {Minimize } \sum i \sum j \frac{x_{i j^{*}} c_{i j}}{n} \]

\[ \text {subject to } \sum j x_{i j}=1 \text { for all } i\]

\[ \sum i \sum j \quad x_{i j} * p_{i j} \leq B\]

\[ x_{i j} \leq 0 \text { for all } i, j \]

Dónde\(x_{ij}\) está la acción\(j\) sobre la sección I,\(c_{ij}\) se pronostica condición con acción\(j\) sobre la sección I, n es el número de segmentos de calzada,\(p_{ij}\) es el costo de acción\(j\) en el segmento I y B es la restricción presupuestal general.

En teoría, el\(x_{ij}\) podría tomar valores no enteros entre 0 y 1 en esta formulación, pero en la práctica, casi todo\(x_{ij}\) lo óptimo sería cero o uno.

Se podrían hacer diversas modificaciones a la formulación básica de la Ec. 5.2.2 a 5.2.6. Para la función objetiva (Ec. 5.2.2), la condición de cada segmento podría ser ponderada por la cantidad de tráfico y el área del segmento. Estos pesos conducirían a la solución óptima para favorecer el trabajo en carreteras muy transitadas y minimizar las condiciones promedio del área de la calzada en lugar de las condiciones promedio del segmento como en la Ec. 5.2.2. Se podrían definir acciones adicionales de mantenimiento vial para extender la restricción Ec. 5.2.3. El problema podría alterarse definiendo las condiciones máximas permitidas como una restricción en cada sección y luego minimizando el costo de lograr esta restricción. Incluso sin cambiar la función objetivo de esta manera, se pueden agregar restricciones de condición máxima permisible si se desea.

Esta estrategia de definición de acciones sobre componentes de infraestructura no se limita a los segmentos de carreteras. Para un gerente de una base militar o un campus, la formulación del problema en las Ecuaciones 5.2.2 - 5.2.5 podría ser utilizada para techos (con reemplazo o mantenimiento como acciones), componentes de aguas pluviales, componentes de edificios o una gama de otros sistemas de infraestructura.

Al formular problemas de programación lineal, es útil abordar una serie de preguntas:

• ¿Cuáles son mis posibles decisiones? ¿Cómo pueden representarse como variables de decisión?
• ¿Cuál es mi objetivo? ¿Se puede representar como una función lineal de mis variables de decisión?
• ¿Cuáles son las restricciones en los valores elegidos de mis variables de decisión? ¿Pueden representarse como funciones lineales de las variables de decisión?

La formulación de problemas es un reto pero es un paso esencial en cualquier optimización. De hecho, la formulación es más desafiante que la solución ya que hay muchos buenos programas de software disponibles para la solución.

El siguiente ejemplo ilustra el uso de las preguntas de formulación.

Problema: Supongamos que desea minimizar el costo de entregar etanol desde un conjunto de instalaciones de producción con un suministro máximo de producción Si donde i va de 1 a n, a un conjunto de instalaciones metropolitanas de mezcla de petróleo (ya que el etanol se mezcla con gasolina) con cantidades requeridas\(P_j\) donde j va de 1 a m. Asumir que el costo de transporte de una instalación de producción a una instalación de mezcla es\(C_{ij}\). Formular un problema de programa lineal para atender la demanda requerida con el menor costo.

• ¿Cuáles son mis posibles decisiones? ¿Cómo pueden representarse como variables de decisión? La cantidad de etanol enviado desde cada instalación de suministro a cada área metropolitana serían mis variables de decisión. Definamos\(x_{ij}\) como la cantidad de etanol enviado desde las instalaciones de producción.
• ¿Cuál es mi objetivo? ¿Se puede representar como una función lineal de mis variables de decisión? La declaración del problema da el objetivo de minimizar los costos de transporte. La función objetiva sería:\(\sum i \sum j c_{i j} * x_{i j}\) que es el costo total de transporte y es lineal con respecto a las variables de decisión.
• ¿Cuáles son las restricciones en los valores elegidos de mis variables de decisión? ¿Pueden representarse como funciones lineales de las variables de decisión? Un conjunto de restricciones es asegurar que el etanol enviado desde cada planta de producción no exceda el suministro disponible:\(\sum i x_{i j} \leq S_{i}\) para cada uno\(i\). Un segundo conjunto de restricciones es asegurar que se satisfaga la demanda en cada área metropolitana:\(\sum i x_{i j} \geq P_{j}\) por cada j área metropolitana. Por último, todos los flujos deben ser positivos:\(x_{i j} \geq 0\).

Hay una variedad de paquetes de software que se pueden utilizar para la programación lineal. Por ejemplo, el programa de hojas de cálculo EXCEL tiene una rutina de optimización llamada Solver. Frontline Systems (2016) tiene un tutorial disponible para el uso de Solver. Los lectores interesados en un tratamiento más profundo de la programación lineal podrían consultar un libro de texto relevante (Boyd y Vandenberghe, 2004).