6.4: Presupuestos e ingresos por uso
- Page ID
- 59584
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Además de las implicaciones de costos de los diferentes niveles de uso de la infraestructura, a menudo hay un efecto de ingresos. Muchos sistemas de infraestructura obtienen ingresos de tarifas de usuarios como ventas de energía o impuestos a la gasolina. A su vez, los presupuestos para el mantenimiento y rehabilitación de la infraestructura dependen de estos ingresos. La alternativa al uso de las tarifas de los usuarios es depender de algún tipo de tributación general, pero esto solo es factible para la infraestructura pública.
Generalmente, las tarifas de usuario se pueden establecer en cualquier nivel. Algunos casos de estrategias de tarifas de usuario son de interés:
- Establecer tarifas de usuario iguales al costo total promedio a corto plazo de proporcionar la infraestructura. En este caso, el proveedor de infraestructura está totalmente financiado y compensado por los costos del servicio de infraestructura.
- Establezca tarifas de usuario iguales a una cantidad que maximice los ingresos totales. Esta estrategia se puede perseguir con un problema de optimización para maximizar los ingresos (\(p*q\)donde\(p\) está la tarifa del usuario y q es el uso de equilibrio) sujeto a la función de demanda (\(q = f(p,x)\)donde\(f(p,x)\) es una función de demanda con el uso dependiente de la tarifa del usuario y otros factores\(x\)). Incluso con una estrategia de maximización de ingresos, el uso puede no ser lo suficientemente alto para cubrir todos los costos de la agencia. Por ejemplo, la autopista de peaje de Pensilvania ha aumentado los peajes cada año de 2008 a 2016 y ha realizado pagos de transferencia a la Commonwealth de Pensilvania, pero los directivos consideran que los ingresos son insuficientes a largo plazo para mantener el sistema de manera efectiva y realizar los pagos de transferencia requeridos (Pittsburgh Post- Gaceta, 2016).
- Establecer tarifas de usuario de acuerdo con la voluntad de pago del usuario. Las curvas de demanda reflejan la voluntad de un individuo a pagar por los servicios de infraestructura. Si la función de costo de usuario cambiara hacia arriba en la Figura 6.3.3, algo de uso desaparecería pero una cantidad restante de demanda de uso continuaría con un costo de usuario mayor. Con un solo costo de usuario, los ingresos estarían aproximadamente\(q_e * p_e\) en la figura 6.3.3 (menos los costos de usuario incurridos directamente en lugar de como precio de servicio). La perfecta discriminación de precios ganaría ingresos iguales al área completa bajo la curva de demanda en la Figura 6.3.3 (nuevamente menos los costos de usuario incurridos directamente). Sin embargo, las personas no suelen revelar su voluntad de pagar por el servicio y existen restricciones para discriminar entre diferentes tipos de usuarios. Sin embargo, se pueden adoptar métodos indirectos, como tarifas aéreas más bajas para compras anteriores o para viajes que impliquen una estadía de sábado por la noche. Los viajeros de negocios con una mayor disposición a pagar tienden a realizar compras tardías y no quedarse en destinos durante un fin de semana.
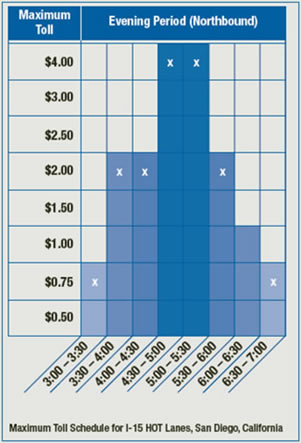
- Establecer tarifas de usuario iguales al costo marginal a corto plazo. Esta es una receta económica común porque esta estrategia minimizará los costos generales siempre que la función de costo marginal a corto plazo incluya todos los costos sociales relevantes (incluidas las externalidades). Los usuarios estarían pagando exactamente el costo asociado con su uso del servicio. Desafortunadamente, es difícil imponer precios de costos marginales a corto plazo exactamente ya que la demanda fluctúa tanto. Un ejemplo de aproximación a esta política aparece en la Figura 6.4.1, donde el peaje en una carretera en San Diego CA aumenta durante los periodos pico de demanda de viajes. Al aumentar los peajes, algunos usuarios serían desviados de la calzada y se evitarían los costos de congestión.