6.5: Costos del Ciclo de Vida, Impuestos y Finanzas de Infraestructura
- Page ID
- 59631
Para la planificación de inversiones de rehabilitación a largo plazo, normalmente se utiliza un punto de vista del ciclo de vida El 'ciclo de vida' en este contexto generalmente se refiere a un horizonte de planeación de inversiones y no necesariamente a la obsolescencia de alguna infraestructura. Al realizar el análisis del ciclo de vida, debe seleccionar un horizonte de planeación adecuado, una tasa de descuento para tener en cuenta el valor del dinero en el tiempo y pronosticar los beneficios y costos de la infraestructura a lo largo del horizonte de planeación.
La selección de un horizonte de planeación y una tasa de descuento suelen ser opciones organizacionales, por lo que la mayoría de los administradores de infraestructura no necesitan preocuparse por estos dos insumos. Para EU, cualquier proyecto que involucre dólares federales deberá utilizar la tasa de descuento elegida por la Oficina de Administración y Presupuesto de Estados Unidos (OMB, 2015). En ausencia de orientación organizacional, un administrador de infraestructura podría usar una tasa de descuento que refleje las tasas de endeudamiento a largo plazo del mercado y un horizonte de planificación consistente con la vida útil esperada de la infraestructura. Por ejemplo, un horizonte de planeación para un edificio podría ser de cincuenta años, mientras que un hub celular podría ser de diez años.
Incluso la formulación de las funciones de costos a corto plazo discutidas anteriormente puede implicar el análisis de costos del ciclo de vida para estimar los costos fijos de la infraestructura en cada período. La infraestructura suele requerir un gran gasto inicial de capital para la construcción, y este costo fijo suele ser anualizado a montos uniformes para obtener los costos fijos asignados a cualquier año de operación. La fórmula para la anualización de un costo inicial\(P\) a montos uniformes\(U\) durante un periodo de planeación con n períodos compuestos a una tasa de descuento\(I\) es (Au, 1992):
\[U=P\left[\frac{i(1+i)^{n}}{(1+i)^{n}-1}\right]\]
Donde\(U\) está el monto anualizado uniforme,\(P\) es el gasto presente,\(i\) es una tasa de descuento y\(n\) es el horizonte de planeación (o técnicamente el número de periodos compuestos). Este proceso equivale al de asumir una hipoteca sobre el componente de infraestructura en la que se toma prestado todo el costo de construcción a una tasa de interés\(i\) y un periodo de amortización de\(n\) años.
¿Por qué el monto uniforme no es simplemente el valor\(P\) dividido por el número de periodos de pago,\(frac{P}{n}\)? El uso de una tasa de descuento refleja el 'valor temporal del dinero'. Los prestamistas suelen requerir un retorno de sus préstamos, por lo que cobran una tasa de interés. Los individuos siempre prefieren recibir dinero en el presente en lugar de una cantidad equivalente en el futuro. El monto de extra requerido para hacer equivalente a una cantidad futura es una tasa de descuento personal. Las tasas de descuento organizacionales generalmente se establecen con referencia al equilibrio del mercado para préstamos a largo plazo.
Además del gasto inicial de construcción de capital, la infraestructura a menudo tendrá grandes gastos asociados con la rehabilitación. La Figura 6.5.1 ilustra este tipo de rehabilitación. La condición del pavimento se deteriora durante el uso y la intemperie hasta que se produce una rehabilitación. Las rehabilitaciones tienen un costo menor que la construcción inicial y se llevan a cabo a lo largo de la vida útil del pavimento. Para la discusión de los métodos de estimación de dichos costos, véase Hendrickson (2008).
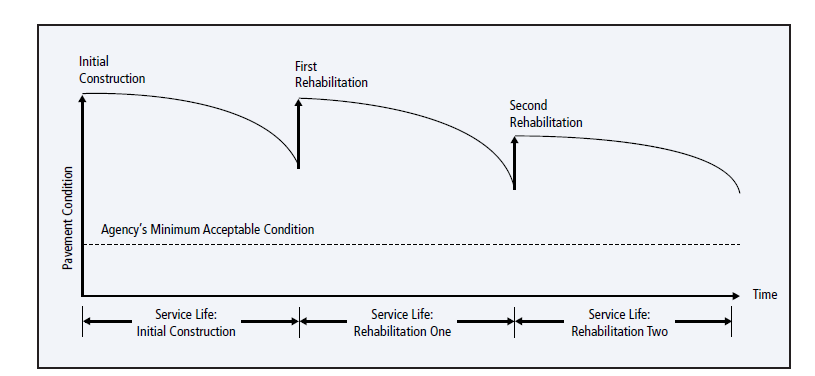
¿Cómo se pueden convertir estos gastos de rehabilitación en un costo anual uniforme? El medio más directo es encontrar el valor actual de dichos costos a lo largo de la vida útil de la infraestructura descontando costos futuros:
\[P=\sum_{(t=o)}^{n} F_{t}(1+i)^{-t}\]
Donde P es valor presente, t es un índice de tiempo, n es el horizonte de planeación, Ft es el costo incurrido en el año t e i es la tasa de descuento. Luego se pueden obtener costos uniformes usando la Ecuación 6.5.1.
Como ejemplo numérico, supongamos que los costos ilustrados en la Figura 6.5.1 se estiman como se muestra en el Cuadro 6.5.1. Con un horizonte de planeación a 30 años y una tasa de descuento del 1%, los costos del ciclo de vida (en $ millones) serían:
\(\text{P = Initial Construction Cost + Discounted First and Second Rehabilitation + Discounted Maintenance Cost}\)
\[=5+\frac{2}{1.01^{10}}+\frac{1}{1.01^{20}}+\sum_{t=1}^{30} 0.1 * 1.01^{-t}\]
\(= 5 + 1.8 + 0.8 + 2.6 = 10.2\)
Para un análisis de costos sociales del pavimento, podrían agregarse los costos de usuario de los retrasos en las carreteras para la construcción.
Cuadro 6.5.1: Ilustración de Costos para un Análisis de Costos del Ciclo de Vida.
| Componente de costo | Año de Ocurencia | Estimación de costos (año base $) |
| InitialConstruction | 0 | 5 millones de dólares |
| Primera Rehabilitación | 10 | $2 millones |
| Segunda Rehabilitación | 20 | 1 millón de dólares |
| Mantenimiento Anual | Cada año 1-30 | $0.1 millones |
La inflación y la deflación afectarán el análisis de costos del ciclo de vida si se utilizan dólares corrientes para el análisis. Con la inflación, el valor de compra de una unidad de moneda disminuye con el tiempo; la deflación refleja un incremento en el valor de una moneda. Los montos actuales en dólares pueden convertirse a montos en dólares 'reales' o del año base aplicando un ajuste del índice de inflación:\(\text(Index_{base year} / Index_t)\) o descontando usando la Ecuación 6.5.2 y la tasa de inflación esperada. Diferentes tipos de infraestructura tienen sus propios índices de inflación o se puede utilizar un índice general como el índice del producto interno bruto. Las estimaciones de costos del ciclo de vida generalmente se realizan en dólares 'reales' del año base. Los acuerdos financieros para pagos como hipotecas generalmente se basan en dólares corrientes. Con estos montos mixtos en dólares, debe aplicar una calculadora de inflación para convertir a un tipo de monto en dólares.
Las tasas de descuento también pueden ser para dólares 'reales' constantes o para dólares inflados actuales. La relación es:
\[I' = I + j = ij\]
Dónde\(I’\) está la tasa de descuento anual incluyendo la inflación (para el descuento en dólares corrientes),\(I\) es la tasa de descuento real, y\(j\) es la tasa de inflación. Los lectores que no estén familiarizados con estos cálculos de economía de ingeniería pueden referirse a Au (1992) u otros libros de texto.
Para las decisiones de inversión, los costos del ciclo de vida pueden compararse con los beneficios del ciclo de vida de manera similar colocando los costos y beneficios en los valores actuales. En este caso, se puede examinar el valor actual neto de una inversión:\( \text(NPV = P_{benefit} – P_{cost})\). Con una serie de opciones de rehabilitación o diseño de infraestructura mutuamente excluyentes, puede seleccionar la que maximice este valor actual neto.
El software de hoja de cálculo o análisis numérico está fácilmente disponible para realizar los cálculos de economía de ingeniería para analizar los costos del ciclo de vida. Para una hoja de cálculo, se utiliza una fila separada (o si prefieres una columna separada) para cada periodo y se registran los costos y beneficios. Las funciones de descuento en las Ecuaciones 6.5.1 y 6.5.2 suelen estar ya disponibles en el software.


