15.1: La precipitación y la disolución
- Page ID
- 1919
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Escribir ecuaciones químicas y expresiones de equilibrio que representen equilibrios de solubilidad.
- Realizar cálculos de equilibrio que involucren solubilidad, expresiones de equilibrio y concentraciones de solutos.
La preservación de muestras de sangre de laboratorio médico, la extracción de agua de mar para obtener el magnesio, la formulación de medicamentos de venta libre como la leche de magnesia y los antiácidos, y el tratamiento de la presencia de agua dura en el suministro de agua de su hogar son solo algunos de los muchos tareas que implican controlar el equilibrio entre un sólido iónico un poco soluble y una solución acuosa de sus iones.
En algunos casos, queremos evitar que se produzca la disolución. La caries dental, por ejemplo, ocurre cuando la hidroxiapatita de calcio, que tiene la fórmula Ca5(PO4)3(OH), en nuestros dientes se disuelve. El proceso de la disolución esta favorecido cuando las bacterias de nuestra boca usan los azúcares de nuestra dieta para producir ácido láctico, que reacciona con los iones de hidróxido de la hidroxiapatita de calcio. Evitando la disolución evita la descomposición. Por otro lado, a veces queremos que una sustancia se disuelva. Queremos que el carbonato de calcio de un antiácido masticable se disuelva porque los iones \(\ce{CO3^2-}\) producidos en este proceso ayudan a aliviar el malestar estomacal.
En esta sección, descubriremos cómo podemos controlar la disolución de un sólido iónico un poco soluble mediante la aplicación del principio de Le Chatelier. También aprenderemos a usar la constante de equilibrio de la reacción para determinar la concentración de los iones presentes en una solución.
La constante del producto de solubilidad
El cloruro de plata se conoce como un sólido iónico escasamente soluble (Figura \(\PageIndex{1}\)). Recuerde de las reglas de solubilidad de un capítulo anterior que los haluros de Ag+ normalmente no son solubles. Sin embargo, cuando agregamos un exceso de AgCl sólido al agua, se disuelve en pequeña medida y produce una mezcla que contiene una solución muy diluida de iones Ag+ y Cl– en equilibrio con cloruro de plata sin disolver:
\[\ce{AgCl}(s)\mathrm{\xrightleftharpoons[\:precipitation\:]{\:dissolution\:}}\ce{Ag+}(aq)+\ce{Cl-}(aq)\]
Este equilibrio, como otros equilibrios, es dinámico; un poco del AgCl sólido se continúa disolviendo, pero al mismo tiempo, los iones Ag+ y Cl– de la solución se combinan para producir una cantidad igual del sólido. En el equilibrio, los procesos opuestos tienen tasas iguales.
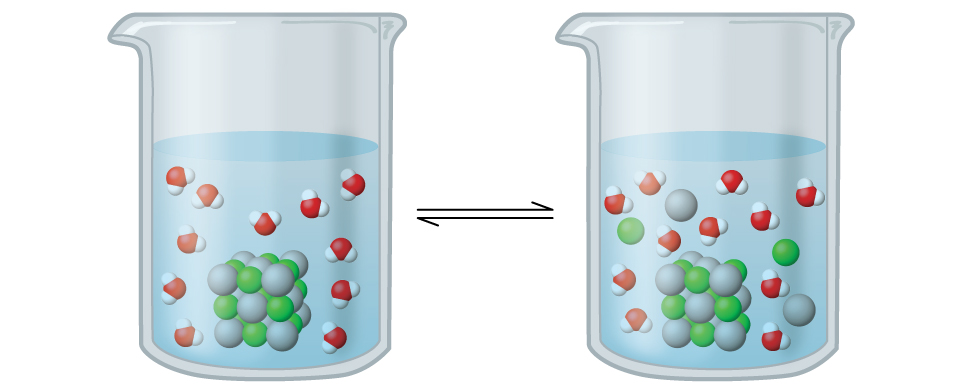
La constante de equilibrio para el equilibrio entre un sólido iónico un poco soluble y una solución de sus iones se llama el producto de solubilidad (Ksp) del sólido. Recuerde del capítulo sobre las soluciones y los coloides que usamos la concentración de un ión como una aproximación de su actividad en una solución diluida. Para el cloruro de plata, en equilibrio:
\[\ce{AgCl}(s) \rightleftharpoons \ce{Ag+}(aq)+\ce{Cl-}(aq) \]
con
\[K_\ce{sp}=[\ce{Ag+}(aq)][\ce{Cl-}(aq)]\]
Cuando examinamos las reacciones de disolución como esta, el sólido es un reactivo, mientras que los iones son productos. La constante del producto de solubilidad, como con todas las expresiones de constante de equilibrio, se escribe como el producto de las concentraciones de cada uno de los iones, elevado a la potencia de sus coeficientes estequiométricos. Aquí, la constante del producto de solubilidad es igual a Ag+ y Cl– cuando una solución de cloruro de plata está en equilibrio con el AgCl no disuelto. No hay un denominador que representa a los reactivos en esta expresión de equilibrio porque el reactivo es un sólido puro; por lo tanto, [AgCl] no aparece en la expresión para Ksp.
| Substancia | Ksp a 25 °C |
|---|---|
| CuCl | 1.2 × 10–6 |
| CuBr | 6.27 × 10–9 |
| AgI | 1.5 × 10–16 |
| PbS | 7 × 10–29 |
| Al(OH)3 | 2 × 10–32 |
| Fe(OH)3 | 4 × 10–38 |
Algunos productos de solubilidad comunes se muestran en la Tabla \(\PageIndex{1}\) según sus valores de Ksp, mientras que en la Tabla E3 aparece una compilación más extensa de productos. Cada una de estas constantes de equilibrio es mucho menor que 1 porque los compuestos en la Tabla \(\PageIndex{1}\) son solo un poco solubles. Una Ksp pequeña representa un sistema en el que el equilibrio se encuentra a la izquierda, de modo que relativamente pocos iones hidratados estarían presentes en una solución saturada.
Ejemplo \(\PageIndex{1}\): Escribiendo ecuaciones y productos de solubilidad
Escriba la ecuación iónica para la disolución y la expresión del producto de solubilidad para cada uno de los siguientes compuestos iónicos un poco solubles:
- AgI, el yoduro de plata, un sólido con propiedades antisépticas.
- CaCO3, el carbonato de calcio, el ingrediente activo en muchos antiácidos masticables de venta libre
- Mg(OH)2, el hidróxido de magnesio, el ingrediente activo de la leche de magnesia.
- Mg(NH4)PO4, el fosfato de magnesio y amonio es una sustancia esencialmente insoluble utilizada en las pruebas de magnesio.
- Ca5(PO4)3OH, el mineral apatito, es una fuente de fosfato para los fertilizantes
(Sugerencia: para determinar cómo convertir (d) y (e) en iones, consulte la lista de los iones poliatómicos en la sección sobre la nomenclatura química).
Solución
- \(\ce{AgI}(s) \rightleftharpoons \ce{Ag+}(aq)+\ce{I-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][I- ]}\)
- \(\ce{CaCO3}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{CO3^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ca^2+][CO3^2- ]}\)
- \(\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Mg^2+][OH- ]^2}\)
- \(\ce{Mg(NH4)PO4}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{NH4+}(aq)+\ce{PO4^3-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Mg^2+][NH4+][PO4^3- ]}\)
- \(\ce{Ca5(PO4)3OH}(s) \rightleftharpoons \ce{5Ca^2+}(aq)+\ce{3PO4^3-}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ca^2+]^5[PO4^3- ]^3[OH- ]}\)
Ejercicio \(\PageIndex{1}\)
Escriba la ecuación iónica para la disolución y el producto de solubilidad para cada uno de los siguientes compuestos un poco solubles:
- BaSO4
- Ag2SO4
- Al(OH)3
- Pb(OH)Cl
- \(\ce{BaSO4}(s) \rightleftharpoons \ce{Ba^2+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ba^2+][SO4^2- ]}\) ;
- \(\ce{Ag2SO4}(s) \rightleftharpoons \ce{2Ag+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+]^2[SO4^2- ]}\);
- \(\ce{Al(OH)3}(s) \rightleftharpoons \ce{Al^2+}(aq)+\ce{3OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Al^3+][OH- ]^3}\);
- \(\ce{Pb(OH)Cl}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{OH-}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Pb^2+][OH- ][Cl- ]}\)
Ahora seguiremos desarrollando nuestra discusión de Ksp y mostraremos cómo la constante del producto de solubilidad se determina a partir de la solubilidad de sus iones, y también cómo se podemos usar Ksp para determinar la solubilidad molar de una sustancia.
Ksp y solubilidad
Recuerde que la definición de solubilidad es la concentración máxima posible de un soluto en una solución a una temperatura y presión determinadas. Podemos determinar el producto de solubilidad de un sólido un poco soluble a partir de esa medida de su solubilidad a una temperatura y presión dadas, siempre que la única reacción significativa que ocurre cuando el sólido se disuelve es su disociación en iones solvatados, es decir, el único equilibrio involucrado es:
\[\ce{M}_p\ce{X}_q(s) \rightleftharpoons p\mathrm{M^{m+}}(aq)+q\mathrm{X^{n−}}(aq)\]
En este caso, calculamos el producto de solubilidad por tomando la solubilidad del sólido expresada en unidades de moles por litro (mol/L), conocida como su solubilidad molar.
Ejemplo \(\PageIndex{2}\): Calculación de Ksp usando las concentraciones de equilibrio
Comenzamos el capítulo con una discusión informal sobre cómo se forma el mineral fluorita. La fluorita, CaF2, es un sólido un poco soluble que se disuelve según la ecuación:
\[\ce{CaF2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2F-}(aq) \nonumber \]
La concentración de Ca2+ en una solución saturada de CaF2 es 2.1 × 10–4 M; por lo tanto, la concentración de de F– es 4.2 × 10–4 M, es decir, el doble de la concentración de Ca2+. ¿Cuál es el producto de solubilidad de la fluorita?
Solución
Primero, escriba la expresión de Ksp, sustituya las concentraciones y resuelva para Ksp:
\[\ce{CaF2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2F-}(aq) \nonumber\]
Una solución saturada es una solución en equilibrio con el sólido. Así:
\[K_\ce{sp}=\ce{[Ca^2+][F-]^2}=(2.1×10^{−4})(4.2×10^{−4})^2=3.7×10^{−11} \nonumber\]
Como ocurre con otras constantes de equilibrio, no incluimos unidades con Ksp.
Ejercicio \(\PageIndex{2}\)
En una solución saturada que está en contacto con el sólido Mg(OH)2, la concentración de Mg2+ es 3.7 × 10–5 M. ¿Cuál es el producto de solubilidad del Mg(OH)2?
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \nonumber\]
Respuesta:
2.0 × 10–13
Ejemplo \(\PageIndex{3}\): Determinación de la solubilidad molar a partir de Ksp
La Ksp de bromuro de cobre (I), CuBr, es 6.3 × 10–9. Calcule la solubilidad molar del bromuro de cobre.
Solución
La constante del producto de solubilidad del bromuro de cobre (I) es 6.3 × 10–9.
La reacción es:
Primero, escriba la expresión de constante de equilibrio para el producto de solubilidad:
\[K_\ce{sp}=\ce{[Cu+][Br- ]}\nonumber\]
Cree una tabla de ICE (como se presentó en el capítulo sobre los conceptos fundamentales de equilibrio), dejando la columna CuBr vacía ya que es un sólido y no contribuye a la Ksp:
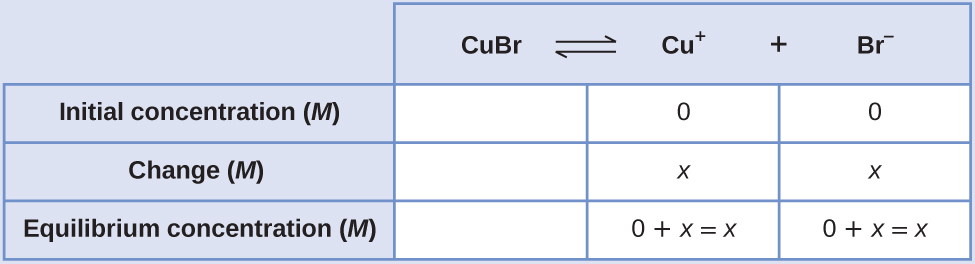
A equilibrio:
Por tanto, la solubilidad molar de CuBr es 7.9 × 10–5 M.
Ejercicio \(\PageIndex{3}\)
La Ksp de AgI es 1.5 × 10–16. Calcule la solubilidad molar del yoduro de plata.
Respuesta:
1.2 × 10–8 M
Ejemplo \(\PageIndex{4}\): Determinación de la solubilidad molar a partir de Ksp, Parte II
Determinación de la solubilidad molar a partir de Ksp, Parte II. La Ksp del hidróxido de calcio, Ca(OH)2, es 8.0 × 10–6. Calcule la solubilidad molar del hidróxido de calcio.
Solución
La constante del producto de solubilidad del hidróxido de calcio es 1.3 × 10–6.
La reacción es:
\[\ce{Ca(OH)2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2OH-}(aq)\nonumber\]
Primero, escriba la expresión de la constante de equilibrio del producto de solubilidad:
\[K_\ce{sp}=\ce{[Ca^2+][OH- ]^2}\nonumber\]
Haga una tabla ICE, dejando la columna Ca(OH)2 vacía, ya que es un sólido y no contribuye a la Ksp:
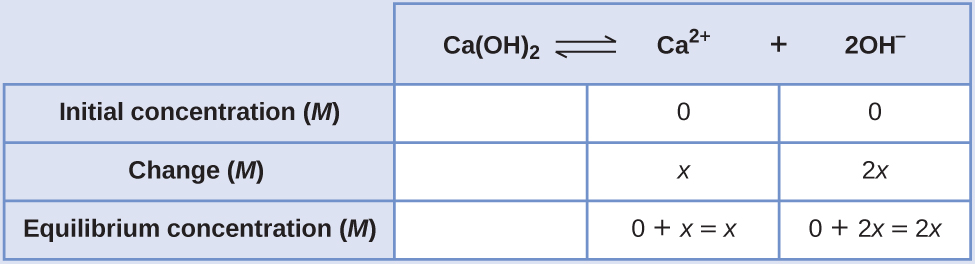
A equilibrio:
Por tanto, la solubilidad molar de Ca(OH)2 es 6.9 × 10–3 M.
Ejercicio \(\PageIndex{4}\)
La Ksp de PbI2 es 1.4 × 10–8. Calcule la solubilidad molar del yoduro de plomo (II).
Respuesta:
1.5 × 10–3 M
Tenga en cuenta que la solubilidad no siempre se da como un valor molar. Cuando la solubilidad de un compuesto se da en alguna unidad diferente que moles por litro, debemos convertir la solubilidad en moles por litro (es decir, molaridad) para usarlo en la expresión de constante del producto de la solubilidad. El ejemplo \(\PageIndex{5}\) muestra cómo hacer esas conversiones de unidades antes de determinar el equilibrio del producto de solubilidad.
Ejemplo \(\PageIndex{5}\): Determinación de Ksp de la solubilidad en gramos
Muchos de los pigmentos utilizados por los artistas en las pinturas a base de aceite (Figura \(\PageIndex{2}\)) son moderadamente solubles en el agua. Por ejemplo, la solubilidad del pigmento de artista, amarillo de cromo, PbCrO4, es de 4.6 × 10–6 g/L. Determine la constante de equilibrio del producto de solubilidad para PbCrO4.

Solución
Se nos da la solubilidad del PbCrO4 en gramos por litro. Si convertimos esta solubilidad en moles por litro, podemos encontrar las concentraciones de equilibrio de Pb2+ y \(\ce{CrO4^2-}\), y luego Ksp:

- Utilice la masa molar de PbCrO4 \(\mathrm{\left(\dfrac{323.2\:g}{1\:mol}\right)}\) para convertir la solubilidad de PbCrO4 en gramos por litro en moles por litro:
\(\mathrm{[PbCrO_4]=\dfrac{4.6×10^{−6}\:g\: PbCrO_4}{1\:L}×\dfrac{1\:mol\: PbCrO_4}{323.2\:g\: PbCrO_4}}\)
\(\mathrm{=\dfrac{1.4×10^{−8}\:mol\: PbCrO_4}{1\:L}}\)
\(=1.4×10^{−8}\:M\)
- La ecuación química para la disolución indica que 1 mol de PbCrO4 produce 1 mol de Pb2+(aq) y 1 mol de \(\ce{CrO_4^{2-}}(aq)\):
\(\ce{PbCrO4}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{CrO4^2-}(aq)\)
Por lo tanto, ambos [Pb2+] y \(\ce{[CrO4^2- ]}\) son iguales a la solubilidad molar de PbCrO4:
\(\ce{[Pb^2+]}=\ce{[CrO4^2- ]}=1.4×10^{−8}\:M\) - Resuelve. Ksp = [Pb2+] \(\ce{[CrO4^2- ]}\) = (1.4 × 10–8)(1.4 × 10–8) = 2.0 × 10–16
Ejercicio \(\PageIndex{5}\)
La solubilidad del TlCl [cloruro de talio (I)], un intermedio que se forma cuando se aísla el talio de los minerales, es de 3.46 gramos por litro a 20 °C. ¿Cuál es su producto de solubilidad?
Respuesta:
2.08 × 10–4
Ejemplo \(\PageIndex{6}\): Calculando la solubilidad de Hg2Cl2
El calomelano, Hg2Cl2, es un compuesto hecho del ion diatómico de mercurio (I), \(\ce{Hg2^2+}\) y los iones de cloruro, Cl–. Aunque la mayoría de los compuestos de mercurio son venenosos, los médicos del siglo XVIII usaban loa calomelanos como un medicamento. Sus pacientes raramente sufrieron la intoxicación por el mercurio debido a los tratamientos porque el calomelano es bastante insoluble:
\[\ce{Hg2Cl2}(s) \rightleftharpoons \ce{Hg2^2+}(aq)+\ce{2Cl-}(aq) \hspace{20px} K_\ce{sp}=1.1×10^{−18} \nonumber\]
Calcule la solubilidad molar de Hg2Cl2.
Solución
La solubilidad molar de Hg2Cl2 es igual a la concentración de los iones \(\ce{Hg2^2+}\) porque para cada mol de Hg2Cl2 que se disuelve, se forma 1 mol de \(\ce{Hg2^2+}\) :

- Determine la dirección del cambio. Antes de que se disuelva el Hg2Cl2, Q es cero y la reacción se desplazará hacia la derecha para alcanzar el equilibrio.
- Determine x y las concentraciones de equilibrio. Las concentraciones y los cambios se dan en la siguiente tabla de ICE:
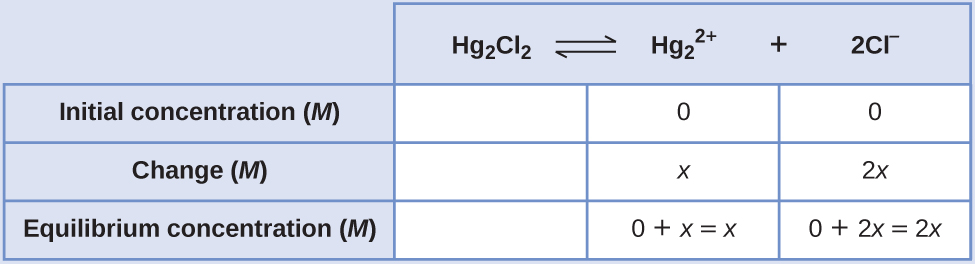
Tenga en cuenta que el cambio en la concentración de Cl- (2x) es dos veces más grande que el cambio en la concentración de \(\ce{Hg2^2+}\) (x) porque 2 mol de Cl- se forma para cada mol de \(\ce{Hg2^2+}\) que se forma. El Hg2Cl2 es un sólido puro por eso no aparece en el cálculo.
- Resuelva para x y las concentraciones de equilibrio. Sustituimos las concentraciones de equilibrio en la expresión de Ksp y calculamos el valor de x:
\(K_\ce{sp}=\ce{[Hg2^2+][Cl- ]^2}\)
La solubilidad molar de Hg2Cl2 es igual a\(\ce{[Hg2^2+]}\), o 6.5 × 10–7 M.
Cheque su trabajo.
A equilibrio, Q = Ksp:
Las calculaciones son iguales.
Ejercicio \(\PageIndex{6}\)
Determine la solubilidad molar del MgF2 a partir de su producto de solubilidad: Ksp = 6.4 × 10–9.
Respuesta1.2 × 10–3 M
Los valores tabulados de Ksp también se pueden comparar con los cocientes de reacción calculados a partir de los datos experimentales para saber si un sólido precipitará en una reacción en condiciones específicas: Q es igual a Ksp en equilibrio; si Q es menos que Ksp, el sólido se disolverá hasta que Q sea igual a Ksp; si Q es más grande que Ksp, la precipitación ocurrirá a una temperatura dada hasta que Q sea igual a Ksp.
El uso de sulfato de bario para imágenes médicas
Se utilizan varios tipos de técnicas de imágenes médicas para ayudar en el diagnóstico de enfermedades de una manera no invasiva. Una de esas técnicas utiliza la ingestión de un compuesto de bario antes de tomar una imagen de rayos X. El paciente ingiere una suspensión de sulfato de bario, un polvo calcáreo. Ya que la Ksp del sulfato de bario es 1.1 × 10-10, muy poco se disuelve cuando cubre el revestimiento del tracto intestinal del paciente. Las áreas cubiertas de bario del tracto digestivo luego aparecen en una radiografía como blancas, lo que permite un mayor detalle visual que una radiografía tradicional (Figura \(\PageIndex{3}\)).
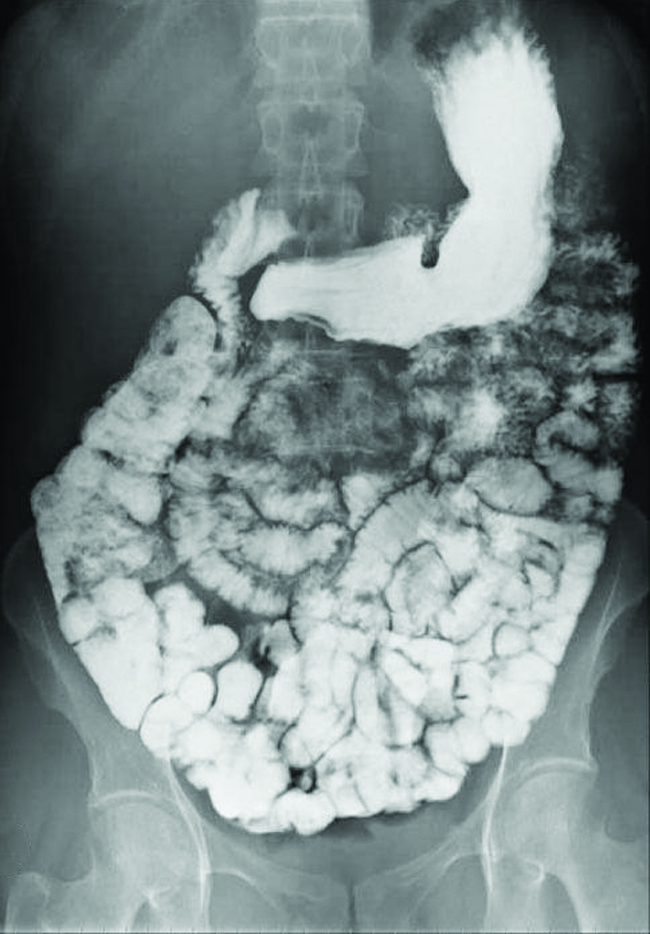
Se pueden completar más pruebas de diagnóstico usando el sulfato de bario y la fluoroscopia. En la fluoroscopia, se pasan rayos X continuamente a través del cuerpo para que el médico pueda monitorear, en una pantalla de televisión o computadora, el movimiento del sulfato de bario mientras pasa por el tracto digestivo. Las imágenes médicas que utilizan el sulfato de bario se pueden utilizar para diagnosticar la enfermedad por el reflujo ácido, la enfermedad de Crohn y las úlceras, además de otras afecciones.
Predecir la precipitación
La ecuación que describe el equilibrio entre el carbonato cálcico sólido y sus iones solvatados es:
\[\ce{CaCO3}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{CO3^2-}(aq)\]
Podemos establecer este equilibrio por agregando carbonato de calcio sólido al agua o mezclando una solución que contiene iones de calcio con una solución que contiene iones de carbonato. Si agregamos carbonato de calcio al agua, el sólido se disolverá hasta que las concentraciones sean tales que el valor del cociente de reacción \(\ce{(Q=[Ca^2+][CO3^2-])}\) sea igual al producto de solubilidad (Ksp = 4.8 × 10–9). Si mezclamos una solución de nitrato de calcio, que contiene iones de Ca2+, con una solución de carbonato de sodio, que contiene iones de \(\ce{CO3^2-}\), el sólido iónico un poco soluble, CaCO3, precipitará siempre que las concentraciones de Ca2+ y \(\ce{CO3^2-}\) iones son tales que Q es mayor que Ksp para la mezcla. La reacción se desplaza hacia la izquierda y las concentraciones de los iones se reducen por la formación del sólido hasta que el valor de Q es igual a Ksp. Se producirá una solución saturada en equilibrio con el sólido no disuelto. Si las concentraciones son tales que Q es menor que Ksp, entonces la solución no está saturada y no se formará ningún precipitado.
Podemos comparar valores numéricos de Q con Ksp para predecir si ocurrirá la precipitación, como muestra el Ejemplo \(\PageIndex{7}\). (Nota: dado que todas las formas de constantes de equilibrio dependen de la temperatura, asumiremos una temperatura ambiente en el futuro en este capítulo, a menos que se especifique explícitamente un valor de temperatura diferente).
Ejemplo \(\PageIndex{7}\): Precipitación de Mg(OH)2
El primer paso en la preparación del magnesio metálico es la precipitación de Mg(OH)2 del agua de mar mediante la adición de cal, Ca(OH)2, una fuente barata de iones de OH– fácilmente disponible:
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=8.9×10^{−12}\]
La concentración de Mg2+ (aq) en el agua de mar es 0.0537 M. ¿El Mg(OH)2 se precipitará cuando se agregue suficiente Ca(OH)2 para dar una [OH–] de 0.0010 M?
Solución
Este problema nos pregunta si la reacción:
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq)\]
se desplaza hacia la izquierda y forma el Mg(OH)2 sólido cuando [Mg2+] = 0.0537 M y [OH–] = 0.0010 M. La reacción se desplaza hacia la izquierda si Q es más grande que Ksp. El cálculo del cociente de la reacción en estas condiciones se muestra aquí:
\[\mathrm{Q=[Mg^{2+}][OH^-]^2=(0.0537)(0.0010)^2=5.4×10^{−8}}\]
Porque Q es más grande que Ksp (Q = 5.4 × 10–8 es más grande que Ksp = 8.9 × 10–12), podemos suponer que la reacción se desplace hacia la izquierda y forma el hidróxido de magnesio sólido. Se forma Mg(OH)2(s) hasta que las concentraciones de ión de magnesio e ión de hidróxido se reducen hasta que el valor de Q sea igual a Ksp.
Ejercicio \(\PageIndex{7}\)
Use los productos de solubilidad en Tabla E3 para determinar si CaHPO4 precipitará de una solución con [Ca2+] = 0.0001 M y \(\ce{[HPO4^2-]}\) = 0.001 M.
Respuesta
El CaHPO4 no precipitará; Q = 1 × 10–7, que es menos que Ksp
Ejemplo \(\PageIndex{8}\): La precipitación del AgCl después de mezclando soluciones
¿El cloruro de plata precipita cuando se mezclan volúmenes iguales de una solución de AgNO3 2.0 × 10–4 M y una solución de NaCl 2.0 × 10–4 M?
(Note: la solución también contiene iones de Na+ y \(\ce{NO3-}\), pero cuando se hace referencia a las reglas de solubilidad, se puede ver que el nitrato de sodio es muy soluble y no puede formar un precipitado).
Solución
La ecuación para el equilibrio entre el cloruro de plata sólido, los iones de plata y los iones de cloruro es:
El producto de solubilidad es 1.8 × 10–10 (Tabla E3).
El AgCl precipitará si el cociente de la reacción calculado a partir de las concentraciones en la mezcla de AgNO3 y NaCl es más grande que Ksp. El volumen se duplica cuando mezclamos volúmenes iguales de soluciones de AgNO3 y NaCl, hasta que se reduce a la mitad de su valor inicial. En consecuencia, inmediatamente después de mezclar, [Ag+] y [Cl–] son ambos iguales a:
El cociente de la reacción, Q, es momentáneamente más grande que Ksp para AgCl, por eso se forma una solución sobresaturada:
Dado que las soluciones sobresaturadas son inestables, el AgCl se precipitará de la mezcla hasta que la solución vuelva al equilibrio, con Q igual a K,.
Ejercicio \(\PageIndex{8}\)
¿El KClO4 se precipitará cuando se agregan 20 mL de una solución de 0.050 M de K+ a 80 mL de una solución de 0.50 M \(\ce{ClO4-}\)? (Recuerde calcular la nueva concentración de cada ion después de mezclar las soluciones antes de introducir la expresión del cociente de la reacción).
Respuesta
No, Q = 4.0 × 10–3 es menos que Ksp = 1.07 × 10–2
En los dos ejemplos anteriores, hemos visto que el Mg(OH)2 o el AgCl se precipitan cuando Q es más grande que Ksp. En general, cuando una solución de una sal soluble del ión Mm+ se mezcla con una solución de una sal soluble del ión Xn–, el sólido, MpXq, precipita si el valor de Q para la mezcla de Mm+ y Xn– es más grande que la Ksp para MpXq. Por lo tanto, si sabemos la concentración de uno de los iones de un sólido iónico un poco soluble y el valor del producto de solubilidad del sólido, entonces podemos calcular la concentración que el otro ion debe exceder para que comience la precipitación. Para simplificar el cálculo, asumiremos que la precipitación comienza cuando el cociente de la reacción se vuelve igual a la constante del producto de solubilidad.
Ejemplo \(\PageIndex{9}\): Precipitación del oxalato de calcio
La sangre no se coagulará si se eliminan los iones de calcio de su plasma. Algunos tubos de extracción de sangre contienen sales del ión oxalato, \(\ce{C2O4^2-}\), para este propósito (Figura \(\PageIndex{4}\)). A concentraciones suficientemente altas, los iones de calcio y oxalato forman un sólido, CaC2O4 • H2O (que también contiene el agua unida al sólido). La concentración de Ca2+ en una muestra de suero sanguíneo es 2.2 × 10–3 M. ¿Qué concentración de ión \(\ce{C2O4^2-} \) se debe establecer antes de que CaC2O4 • H2O comience a precipitar?
Solución
La expresión de equilibrio es:
Para esta reacción (Tabla E3):
el CaC2O4 No aparece en esta expresión porque es un sólido. El agua no aparece porque es el solvente.
El CaC2O4 sólido no se empieza a formar hasta que Q este igual a Ksp. Porque sabemos Ksp o [Ca2+], podemos resolver para la concentración de \(\ce{C2O4^2-}\) que es necesario para producir el primer rastro del sólido:
Es necesaria una concentración de \(\ce{[C2O4^2-]}\) = 8.9 × 10–6 M para iniciar la precipitación de CaC2O4 en estas condiciones.
Ejercicio \(\PageIndex{9}\)
Si una solución contiene 0.0020 mol de \(\ce{CrO4^2-}\) por litro, ¿qué concentración de ion Ag+ se debe alcanzar cuando se agrega AgNO3 sólido antes de que Ag2CrO4 comience a precipitar? Ignore cualquier aumento de volumen al agregar el nitrato de plata sólido.
Respuesta:4.5 × 10–9 M
A veces es útil saber la concentración de un ion que permanece en solución después de la precipitación. También podemos usar el producto de solubilidad para este cálculo: si sabemos el valor de Ksp y la concentración de un ion en solución, podemos calcular la concentración del segundo ion que permanece en solución. El cálculo es del mismo tipo que el del Ejemplo \(\PageIndex{8}\): cálculo de la concentración de una especie en una mezcla de equilibrio a partir de las concentraciones de las otras especies y la constante de equilibrio. Sin embargo, las concentraciones son diferentes; estamos calculando concentraciones después de que se completa la precipitación, en lugar de al comienzo de la precipitación.
Ejemplo \(\PageIndex{10}\): Concentraciones después de la precipitación
La ropa lavada en el agua que tiene una concentración de manganeso [Mn2+ (aq)] mas grande que 0.1 mg/L (1.8 × 10–6 M) se puede manchar con el manganeso al oxidarse, pero la cantidad de Mn2+ en el agua se puede reducir si agregamos una base. Si una persona que lava la ropa desea agregar un tampón para mantener el pH lo suficientemente alto como para precipitar el manganeso como hidróxido, Mn(OH)2, ¿qué pH se requiere para mantener [Mn2+] igual a 1.8 × 10–6 M?
Solución
La disolución del Mn(OH)2 se describe por la ecuación:
\[\ce{Mn(OH)2}(s) \rightleftharpoons \ce{Mn^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=2×10^{−13}\]
Necesitamos calcular la concentración de OH– cuando la concentración de Mn2+ es 1.8 × 10–6 M. A partir de eso, calculamos el pH. En equilibrio:
o
entonces
Ahora calculamos el pH a partir del pOH
Si la persona que lava la ropa agrega una base, como el silicato de sodio (Na4SiO4) en algunos detergentes, al agua de lavado hasta que el pH suba a 10.52, el ion manganeso se reducirá a una concentración de 1.8 × 10–6 M; a esa concentración o menos, el ion no manchará la ropa.
Ejercicio \(\PageIndex{1}\)0
El primer paso en la preparación del magnesio metálico es la precipitación de Mg(OH)2 del agua de mar mediante la adición de Ca(OH)2. La concentración de Mg2+ (aq) en el agua de mar es 5.37 × 10–2 M. Calcule el pH al cual [Mg2+] disminuye a 1.0 × 10–5 M por la adición de Ca(OH)2.
Respuesta:10.97
Debido a su sensibilidad a la luz, las mezclas de haluros de plata se utilizan en la fibra óptica para láseres médicos, en lentes de anteojos fotocromáticos (lentes de vidrio que se oscurecen automáticamente cuando se exponen a la luz solar) y, antes de la llegada de la fotografía digital, en películas fotográficas. Aunque AgCl (Ksp = 1.6 × 10-10), AgBr (Ksp = 5.0 × 10-13) y AgI (Ksp = 1.5 × 10-16) son bastante insolubles, no podemos preparar una mezcla sólida homogénea de ellos por agregando Ag+ a una solución de Cl–, Br– e I–; esencialmente todo el AgI precipitará antes de que se forme cualquiera de los otros haluros sólidos debido a su menor valor de Ksp. Sin embargo, podemos preparar una mezcla homogénea de sólidos agregando lentamente una solución de Cl–, Br– e I– a una solución de Ag+.
Cuando dos aniones forman compuestos un poco solubles con el mismo catión, o cuando dos cationes forman compuestos un poco solubles con el mismo anión, el compuesto menos soluble (generalmente, el compuesto con la Ksp más pequeña) generalmente precipita primero cuando agregamos un agente precipitante a un solución que contiene ambos aniones (o ambos cationes). Cuando los valores de Ksp de los dos compuestos difieren en dos órdenes de magnitud o más (p. Ej., 10-2 vs. 10-4), casi todos los compuestos menos solubles precipitan antes que cualquiera de los más solubles. Este es un ejemplo de precipitación selectiva, donde se agrega un reactivo a una solución de iones disueltos haciendo que uno de los iones precipite antes que el resto.
El rol de la precipitación en el tratamiento de aguas residuales
Los equilibrios de solubilidad son herramientas útiles en el tratamiento de aguas residuales que se llevan a cabo en instalaciones que pueden tratar el agua municipal en su ciudad o pueblo (Figura \(\PageIndex{5}\)). Específicamente, la precipitación selectiva se utiliza para eliminar los contaminantes de las aguas residuales antes de que se vuelvan a liberar en los cuerpos de agua naturales. Por ejemplo, los iones de fosfato \(\ce{(PO4^2-)}\) a menudo están presentes en el agua descargada de las instalaciones de fabricación. La abundancia de fosfato hace que crezca un exceso de algas, lo que afecta la cantidad de oxígeno disponible para la vida marina y hace que el agua no sea apta para el consumo humano.

Una forma común de eliminar los fosfatos del agua es mediante la adición del hidróxido de calcio, conocido como cal, Ca(OH)2. La cal se convierte en carbonato de calcio, una base fuerte, en el agua. A medida que el agua se vuelve más básica, los iones de calcio reaccionan con los iones de fosfato para producir la hidroxiapatita, Ca5(PO4)3(OH), que luego precipita de la solución:
\[\ce{5Ca^2+ + 3PO4^3- + OH- \rightleftharpoons Ca10(PO4)6⋅(OH)2}(s)\]
Luego, el precipitado se elimina por la filtración y el agua se lleva de nuevo a un pH neutro mediante la adición de CO2 en un proceso de recarbonatación. También se pueden utilizar otros productos químicos para la eliminación de fosfatos por precipitación, incluidos el cloruro de hierro (III) y el sulfato de aluminio.
La precipitación selectiva también se puede utilizar en los análisis cualitativos. En este método, los reactivos se agregan a una mezcla química desconocida para inducir la precipitación. Ciertos reactivos provocan la precipitación de los iones específicos; por lo tanto, la adición del reactivo se puede usar para determinar si el ion está presente en la solución.
Ejemplo \(\PageIndex{11}\): Precipitación de los haluros de plata
Una solución contiene 0.0010 mol de KI y 0.10 mol de KCl por litro. Se agrega gradualmente AgNO3 a esta solución. ¿Qué se forma primero, el AgI sólido o el AgCl sólido?
Solución
Los dos equilibrios involucrados son:
Si la solución contiene concentraciones aproximadamente iguales de Cl– e I–, entonces la sal de plata con la Ksp (AgI) más pequeña precipitaría primero. Sin embargo, las concentraciones no son iguales, por eso debemos encontrar la [Ag+] en la que AgCl comienza a precipitar y la [Ag+] en la que AgI comienza a precipitar. La sal que se forma a la [Ag+] más baja precipita primero.
Para AgI: El AgI precipita cuando Q es igual a Ksp para AgI (1.5 × 10–16). Cuando [I–] = 0.0010 M:
AgI empieza a precipitar cuando [Ag+] es 1.5 × 10–13 M.
Para AgCl: AgCl precipita cuando Q es igual a Ksp para AgCl (1.6 × 10–10). Cuando [Cl–] = 0.10 M:
AgCl comienza a precipitar cuando [Ag+] es 1.6 × 10–9 M.
AgI comienza a precipitar a una concentración de [Ag+] más baja que AgCl, por eso AgI comienza a precipitar primero.
Ejercicio \(\PageIndex{11}\)
Si se agrega una solución de nitrato de plata a una solución que es 0.050 M en los iones Cl– y Br–, ¿en qué concentración de [Ag+] comenzará la precipitación y cuál será la fórmula del precipitado?
Respuesta
[Ag+] = 1.0 × 10–11 M; AgBr se precipitará primero
El efecto del ion común
Como vimos cuando hablamos de las soluciones de búfer, la concentración de los iones hidronio de una solución acuosa de ácido acético disminuye cuando se agrega el acetato de sodio, un electrolito fuerte, NaCH3CO2. Podemos explicar este efecto utilizando el principio de Le Chatelier. La adición de los iones de acetato hace que el equilibrio se desplace hacia la izquierda, disminuyendo la concentración de \(\ce{H3O+}\) para compensar por el aumento en la concentración de los iones acetato. Esto aumenta la concentración de CH3CO2H:
\[\ce{CH3CO2H + H2O \rightleftharpoons H3O+ + CH3CO2-}\)]
Debido a que el acetato de sodio y el ácido acético tienen el ion de acetato en común, el efecto sobre el equilibrio se llama el efecto del ion común. El efecto del ion común también puede tener un efecto directo en los equilibrios de solubilidad. Supongamos que estamos examinando la reacción en la que se disuelve el yoduro de plata:\[\ce{AgI}(s) \rightleftharpoons \ce{Ag+}(aq)+\ce{I-}(aq)\]
Si tuviéramos que agregar el yoduro de potasio (KI) a esta solución, estaríamos agregando una sustancia que tiene un ion en común con el yoduro de plata. El principio de Le Chatelier nos dice que cuando ocurre un cambio en un sistema en equilibrio, la reacción cambiará para contrarrestar ese cambio. En este ejemplo, habría un exceso de iones de yoduro, lo que causaría que la reacción se desplazaría hacia la izquierda, lo que haría que precipitara más yoduro de plata de la solución.
Ejemplo \(\PageIndex{12}\): El efecto del ion común
Calcule la solubilidad molar del sulfuro de cadmio (CdS) en una solución de 0.010-M bromuro de cadmio (CdBr2). La Ksp de CdS es 1.0 × 10–28.
Solución
Lo primero que debemos notar es que el sulfuro de cadmio se disuelve en una solución que contiene iones de cadmio. Necesitamos usar una tabla de ICE para empezar este problema e incluir la concentración de CdBr2 como un contribuyente de iones de cadmio:
\[\ce{CdS}(s) \rightleftharpoons \ce{Cd^2+}(aq)+\ce{S^2-}(aq)\]
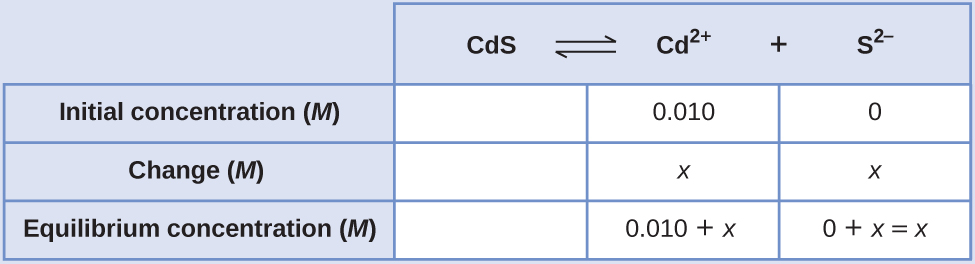
Podemos resolver esta ecuación usando la fórmula cuadrática, pero también podemos hacer una suposición para hacer este cálculo mucho más simple. Dado que el valor de Ksp es tan pequeño en comparación con la concentración del cadmio, podemos suponer que el cambio entre la concentración inicial y la concentración de equilibrio es insignificante, de modo que 0.010 + x ~ 0.010. Regresando a nuestra expresión de Ksp, obtendríamos:
Por eso, la solubilidad molar de CdS en esta solución es 1.0 × 10–26 M.
Ejercicio \(\PageIndex{12}\)
Calcule la solubilidad molar del hidróxido de aluminio, Al(OH)3, en una solución de 0.015 M nitrato de aluminio., Al(NO3)3. La Ksp de Al(OH)3 es 2 × 10–32.
Respuesta:
4 × 10–11
Resumen
La constante de equilibrio para un equilibrio que involucra la precipitación o la disolución de un sólido iónico un poco soluble se llama el producto de solubilidad, Ksp, del sólido. Cuando tenemos un equilibrio heterogéneo que involucra al sólido un poco soluble MpXq y sus iones Mm+ y Xn–:
\[\ce{M}_p\ce{X}_q(s) \rightleftharpoons p\mathrm{M^{m+}}(aq)+q\mathrm{X^{n−}}(aq) \nonumber\]
Escribimos la expresión del producto de solubilidad como:
\[K_\ce{sp}=\mathrm{[M^{m+}]}^p\mathrm{[X^{n−}]}^q \nonumber\]
El producto de solubilidad de un electrolito un poco soluble se puede calcular a partir de su solubilidad; a la inversa, su solubilidad se puede calcular a partir de su Ksp, siempre que la única reacción significativa que se produce cuando el sólido se disuelve es la formación de sus iones. Un electrolito un poco soluble comienza a precipitar cuando la magnitud del cociente de la reacción para la reacción de disolución excede la magnitud del producto de la solubilidad. La precipitación continúa hasta que el cociente de la reacción es igual al producto de la solubilidad. Se puede agregar un reactivo a una solución de iones para permitir que un ion precipite selectivamente de la solución. El efecto del ion común también puede tener un efecto en las reacciones de precipitación. En la presencia de un ion en común con uno de los iones en la solución, se aplica el principio de Le Chatelier y queda más precipitado de la solución, lo que hace que se reduzca la solubilidad molar.
Glosario
- el efecto de los iones comunes
- efecto sobre el equilibrio cuando se añade a la solución una sustancia con un ion en común con las especies disueltas; causa una disminución en la solubilidad de una especie iónica, o una disminución en la ionización de un ácido o base débil
- solubilidad molar
- solubilidad de un compuesto expresada en unidades de moles por litro (mol/L)
- precipitación selectiva
- proceso en el que los iones se separan usando diferencias en su solubilidad con un reactivo de precipitación dado
- producto de solubilidad (Ksp)
- constante de equilibrio para la disolución de un electrolito un poco soluble
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


