5.1: El origen de la señal NMR
- Page ID
- 2342
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.1A: Núcleos RMN-activos
La base de la resonancia magnética nuclear es la observación de que muchos núcleos atómicos giran alrededor de un eje y generan su propio campo magnético, o momento magnético. Por razones que están fuera del alcance de este texto, sólo los núcleos con un número impar de protones y/o neutrones tienen un momento magnético. Afortunadamente para los químicos, varios núcleos comunes, incluyendo hidrógeno (1H), el isótopo 13C de carbono, el isótopo 19F de flúor, y el isótopo 31P de fósforo, todos tienen momentos magnéticos y por lo tanto pueden ser observados por RMN - ellos son, en otras palabras, RMN-activos. Otros núcleos - tales como los isótopos comunes 12C y 16O de carbono y oxígeno - no tienen momentos magnéticos, y son esencialmente invisibles en la RMN. Otros núcleos tales como deuterio (2H) y nitrógeno (14N) tienen momentos magnéticos y son RMN-activos, pero la naturaleza de sus momentos magnéticos es tal que estos núcleos son más difíciles de analizar por RMN. En la práctica es 1H, 13C, 19F, y 31P los que son más a menudo observados por espectroscopía de RMN. En este capítulo, vamos a desarrollar nuestra comprensión de los principios detrás de la espectroscopía de RMN al enfocar nuestra atención primero en la detección de protones en experimentos de RMN-1H (en la discusión acerca de RMN, los términos 'hidrógeno' y 'protón' se utilizan indistintamente). Gran parte de lo que aprendemos, sin embargo, también se aplicará a la detección y análisis de otros núcleos activos de RMN, y más adelante en el capítulo vamos a cambiar nuestra atención hacia los experimentos de RMN que involucran átomos de 13C y 31P.
5.1B: Precesión nuclear, estados de espín, y la condición de resonancia
Cuando una muestra de un compuesto orgánico está sentado en un matraz en una mesa de trabajo de laboratorio, los momentos magnéticos de sus átomos de hidrógeno están orientadaos al azar. Cuando la misma muestra se coloca dentro del campo de un imán muy fuerte en un instrumento de RMN (este campo se conoce por RMN espectroscopistas como el campo aplicado, abreviado B0) cada hidrógeno asumirá uno de los dos posibles estados de espín. En lo que se conoce como el estado de +½ espín, el momento magnético del hidrógeno está alineado con la dirección de B0, mientras que en el estado de -½ espín esta alineado en oposición a la dirección de B0.
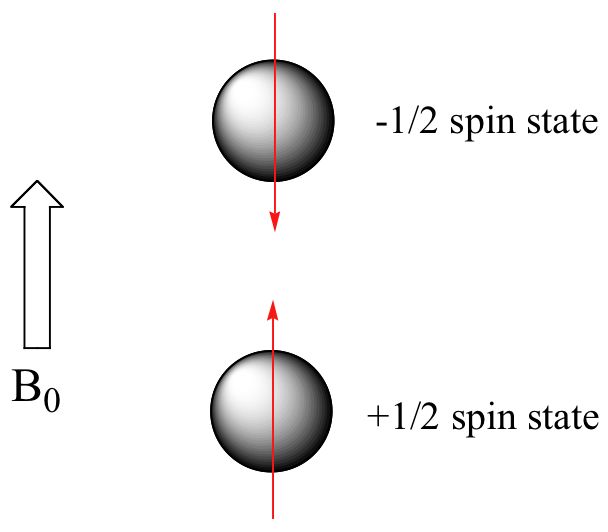
Debido a que el estado de espín ½ + es ligeramente de menor energía, en una gran población de moléculas orgánicas poco más de la mitad de los átomos de hidrógeno ocuparán este estado, mientras que un poco menos de la mitad ocupará el estado -½. La diferencia en energía entre los dos estados de giro aumenta al aumentar la fuerza de B0. Esta última afirmación está en cursiva porque es una de las ideas claves en la espectroscopía de RMN, como veremos más adelante.
En este punto, tenemos que mirar un poco más de cerca cómo un protón gira en un campo magnético aplicado. Usted puede recordar haber jugar con trompos como un niño. Cuando un trompo se desacelera un poco y el eje de giro ya no es completamente vertical, comienza a exhibir movimiento de precesión, mientras el eje de rotación gira lentamente alrededor de la vertical. Del mismo modo, átomos de hidrogeno girando en un campo magnético aplicado exhiben también movimiento de precesión alrededor de un eje vertical. Es este eje (que es ya sea paralelo o antiparalelo a B0) que define el momento magnético del protón. En la figura de abajo, el protón está en el estado de espín ½ +.
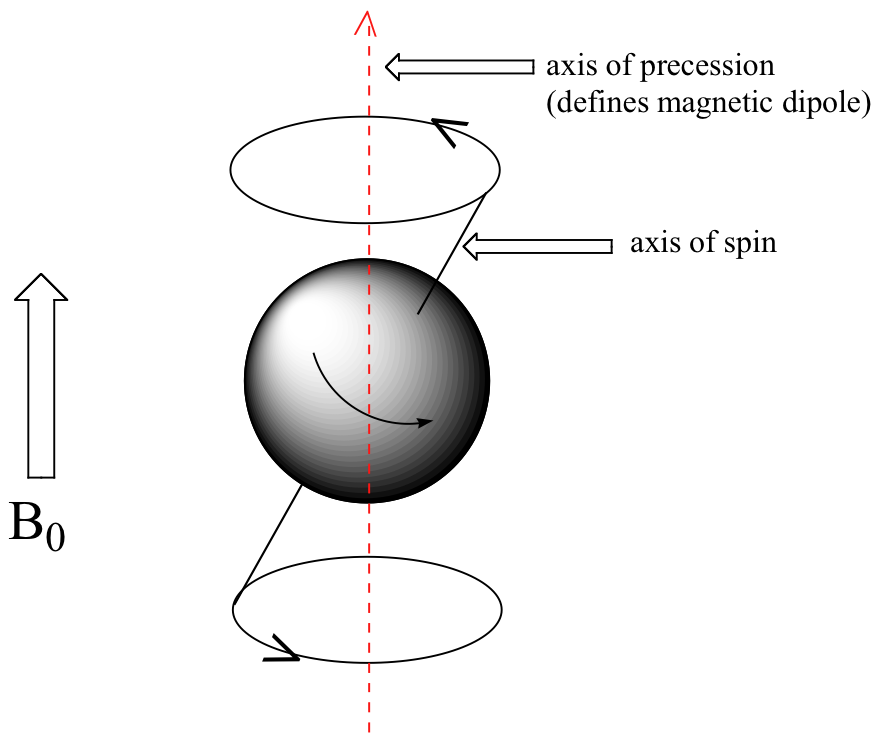
La frecuencia de precesión (también llamada la frecuencia de Larmor, abreviado ωL) es simplemente el número de veces por segundo que el protón viaja en un círculo completo. La frecuencia de precesión de un proton aumenta con la fuerza de B0.
Si un protón que esta viajando en un campo magnético aplicado se expone a radiación electromagnética de una frecuencia ν que coincide con su frecuencia de precesión ωL, tenemos una condición llamada resonancia. En la condición de resonancia, un protón en el estado de espín de menor energía ½ + (alineado con B0) hará la transición (flip) hacia la energía superior estado de espín -½ (opuesto a B0). Al hacerlo, absorberá la radiación a esta frecuencia de resonancia ν = ωL. Esta frecuencia, como es posible que ya haya adivinado, corresponde a la diferencia de energía entre los dos estados de spin del protón. Con los fuertes campos magnéticos generados por los imanes superconductores utilizado en instrumentos de RMN modernos, la frecuencia de resonancia de protones cae dentro del rango de ondas de radio, en cualquier lugar desde 100 MHz a 800 MHz, dependiendo de la fuerza del imán.


