8.5: Grupos salientes
- Page ID
- 2373
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)8.5A: What makes a good leaving group?
In our general discussion of nucleophilic substitution reactions, we have until now been designating the leaving group simply as “X". As you may imagine, however, the nature of the leaving group is an important consideration: if the C-X bond does not break, the new bond between the nucleophile and electrophilic carbon cannot form, regardless of whether the substitution is SN1 or SN2.
When the C-X bond breaks in a nucleophilic substitution, the pair of electrons in the bond goes with the leaving group. In this way, the leaving group is analogous to the conjugate base in a Brønsted-Lowry acid-base reaction. When we were evaluating the strength of acids in chapter 7, what we were really doing was evaluating the stability of the conjugate base that resulted from the proton transfer. All of the concepts that we used to evaluate the stability of conjugate bases we can use again to evaluate leaving groups – essentially they are one and the same. In other words, the trends in basicity are parallel to the trends in leaving group potential - the weaker the base, the better the leaving group. Just as with conjugate bases, the most important question regarding leaving groups is this: when a leaving group leaves and takes a pair of electrons with it, how well is the extra electron density stabilized?
In laboratory synthesis reactions, halides often act as leaving groups. Iodide, which is the least basic of the four main halides, is also the best leaving group – it is the most stable as a negative ion. Fluoride is the least effective leaving group among the halides, because fluoride anion is the most basic.
Exercise 8.13: In each pair (A and B) below, which electrophile would be expected to react more rapidly in an SN2 reaction with the thiol group of cysteine as the common nucleophile?

We already know (section 8.3C) that the use of polar, aprotic solvents increases the reactivity of nucleophiles in SN2 reactions, because these solvents do not 'cage' the nucleophile and keep it from attacking the electrophile.
On the other hand, the rates of SN1 reactions are generally increased by the use of a highly polar solvent, including protic (hydrogen bonding) solvents such as water or ethanol. In essence, a protic solvent increases the reactivity of the leaving group in an SN1 reaction, by helping to stabilize the products of the first (ionization) step. In the SN1 mechanism, remember, the rate determining step does not involve the nucleophilic species, so any reduction of nucleophilicity does not matter. What matters is that the charged products of the first step - the carbocation intermediate and the anionic leaving group - are stabilized best by a highly polar, protic solvent.
8.5B: Leaving groups in biochemical reactions
In biological reactions, we do not often see halides serving as leaving groups (in fact, outside of some marine organisms, halogens are fairly unusual in biological molecules). More common leaving groups in biochemical reactions are phosphates, water, alcohols, and thiols. In many cases, the leaving group is protonated by an acidic group on the enzyme as bond-breaking occurs. For example, hydroxide ion itself seldom acts as a leaving group – it is simply too high in energy (too basic). Rather, the hydroxide oxygen is generally protonated by an enzymatic acid before or during the bond-breaking event, resulting in a (very stable) water leaving group.

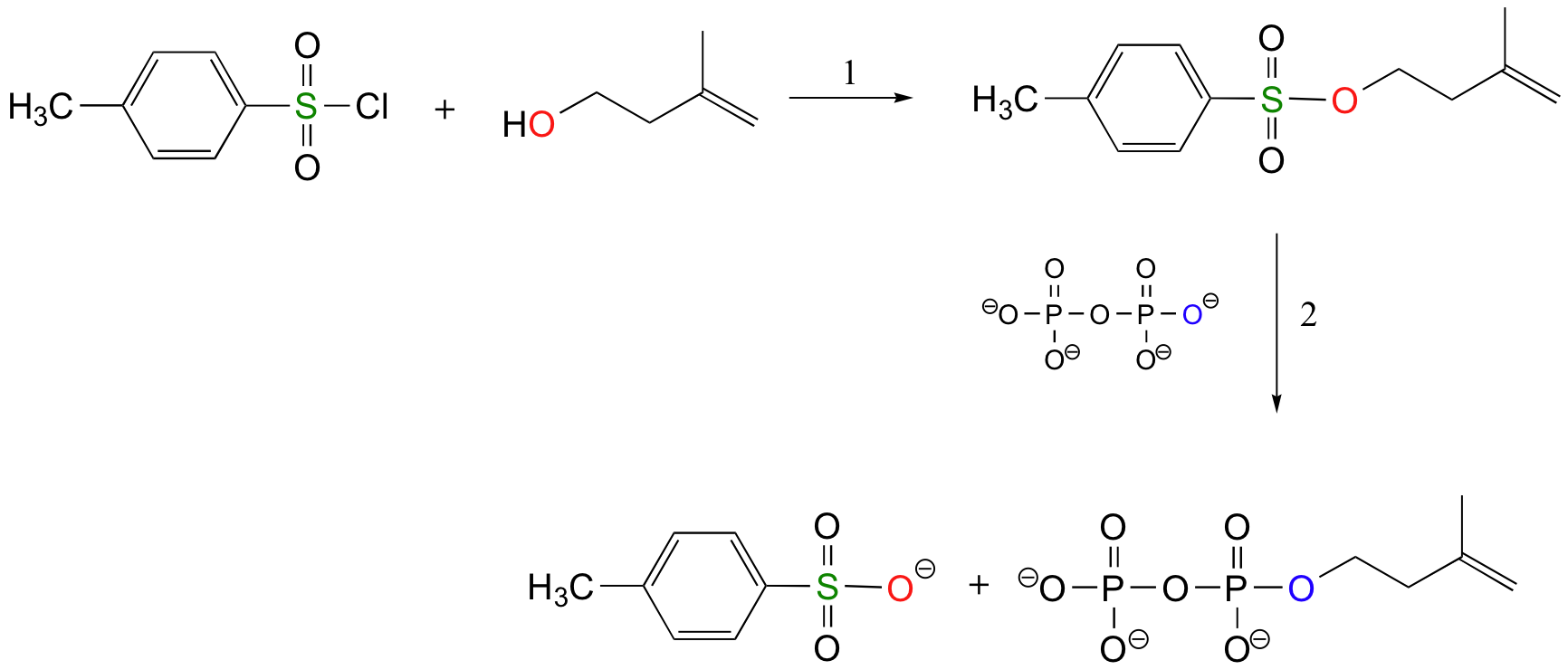
More often, however, the hydroxyl group of an alcohol is first converted enzymatically to a phosphate ester in order to create a better leaving group. This phosphate ester can take the form of a simple monophosphate (arrow 1 in the figure below), a diphosphate (arrow 2), or a nucleotide monophosphate (arrow 3).
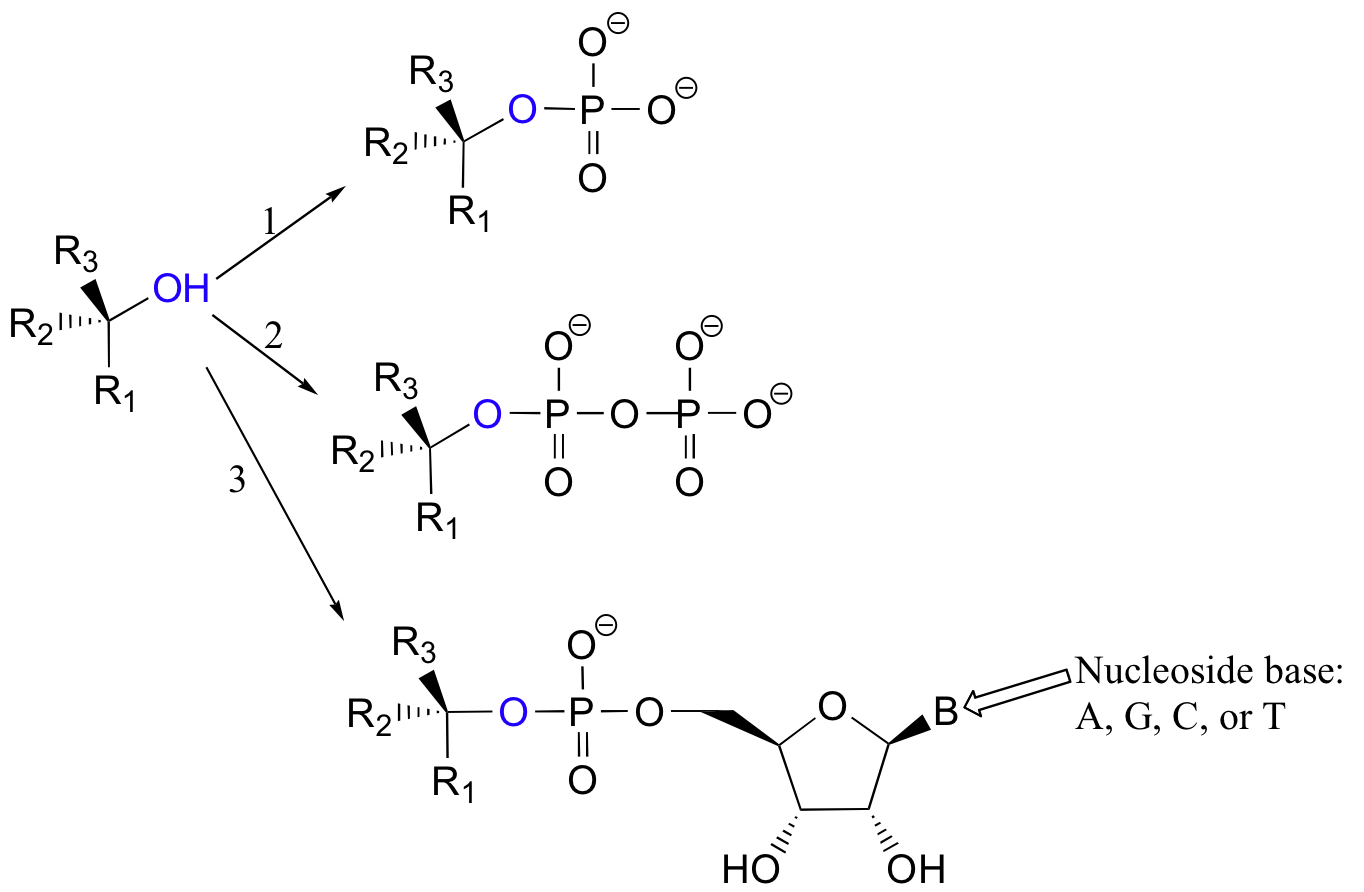
Due to resonance delocalization of the developing negative charge, phosphates are excellent leaving groups.

Here’s a specific example (from DNA nucleotide biosynthesis) that we will encounter in more detail in section 11.5:
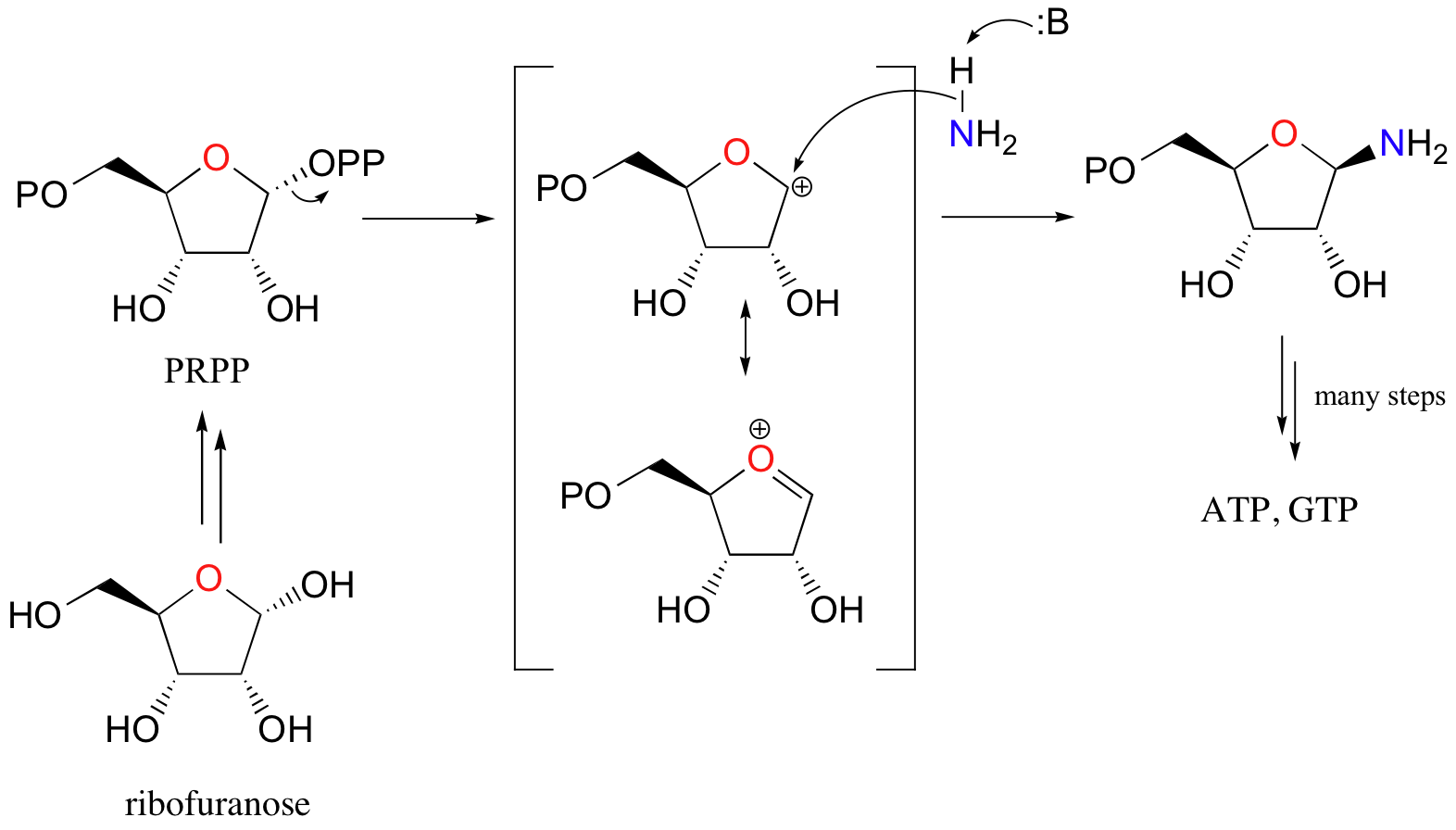
Here, the OH group on ribofuranose is converted to a diphosphate, a much better leaving group. Ammonia is the nucleophile in the second step of this SN1-like reaction.
We will learn much more about phosphates in chapter 10. What is important for now is that in each case, an alcohol has been converted into a much better leaving group, and is now primed for a nucleophilic substitution reaction.
8.5C: Synthetic parallel - conversion of alcohols to alkyl halides, tosylates and mesylates
Synthetic organic chemists, when they want to convert an alcohol into a better leaving group, have several methods to choose from. One common strategy is to convert the alcohol into an alkyl chloride or bromide, using thionyl chloride or phosphorus tribromide:


We won’t worry yet about the mechanism for the thionyl chloride reaction (you’ll have a chance to propose a mechanism for this reaction in the chapter 12 problems), but the PBr3 reaction is thought to involve two successive SN2-like steps:
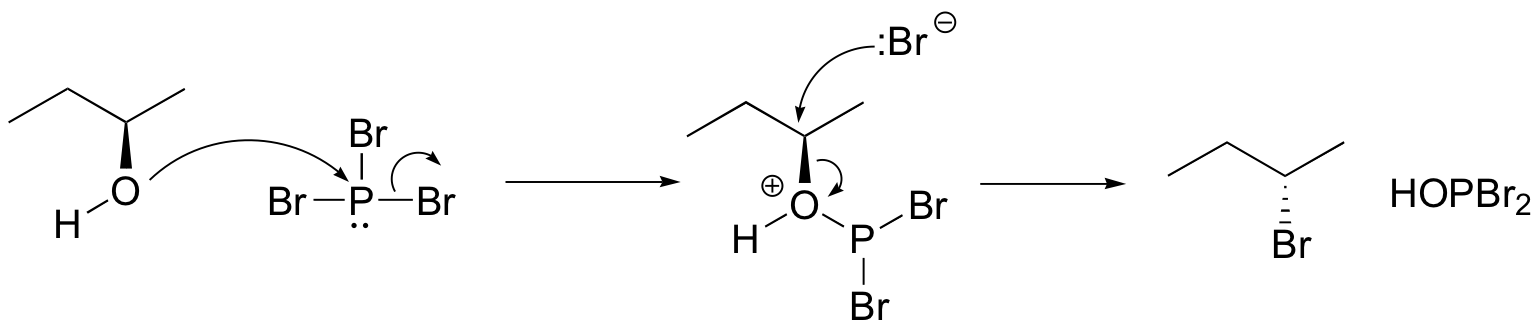
Notice that these reactions result in inversion of stereochemistry in the resulting alkyl halide.
Alternatively, we can transform an alcohol group into sulfonic ester using para-toluene sulfonyl chloride (Ts-Cl) or methanesulfonyl chloride (Ms-Cl), creating what is termed an organic tosylate or mesylate:
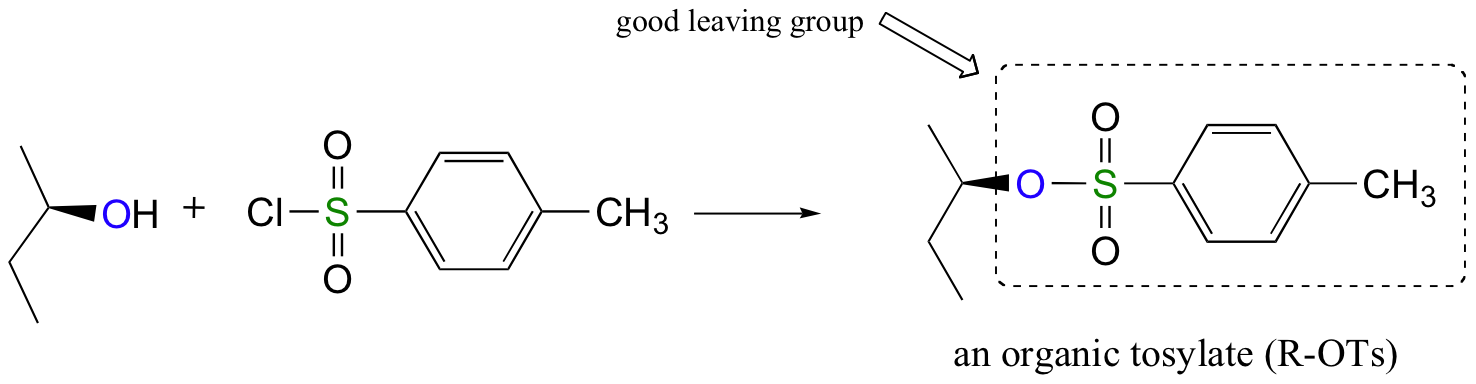
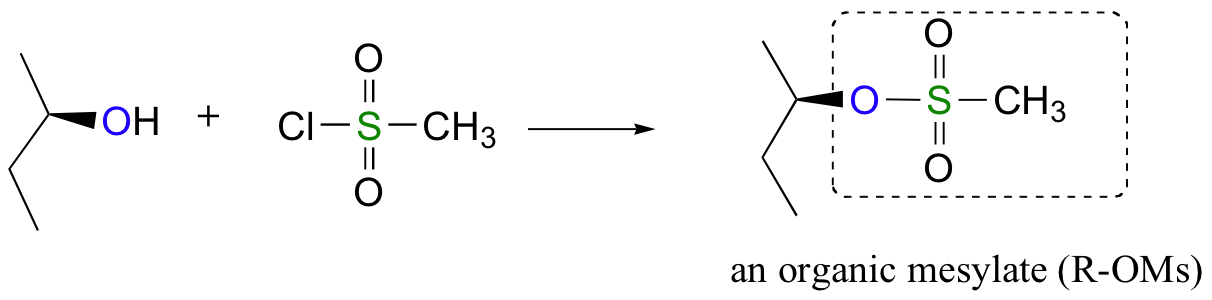
Again, you’ll have a chance to work a mechanism for tosylate and mesylate formation in the chapter 12 problems. Notice, though, that unlike the halogenation reactions above, conversion of an alcohol to a tosylate or mesylate proceeds with retention of configuration at the electrophilic carbon.
Chlorides, bromides, and tosylate / mesylate groups are excellent leaving groups in nucleophilic substitution reactions, due to resonance delocalization of the developing negative charge on the leaving oxygen.

The laboratory synthesis of isopentenyl diphosphate - the 'building block' molecule used by nature for the construction of isoprenoid molecules such as cholesterol and b-carotene - was accomplished by first converting the alcohol into an organic tosylate (step 1), then displacing the tosylate group with an inorganic pyrophosphate nucleophile (step 2) (J. Org. Chem 1986, 51, 4768).
Exercise 8.14: Predict the structures of A and B in the following reaction:

8.5D: Predicting SN1 vs. SN2 mechanisms; competition between nucleophilic substitution and elimination reactions
When considering whether a nucleophilic substitution is likely to occur via an SN1 or SN2 mechanism, we really need to consider three factors:
1) The electrophile: when the leaving group is attached to a methyl group or a primary carbon, an SN2 mechanism is favored (here the electrophile is unhindered by surrounded groups, and any carbocation intermediate would be high-energy and thus unlikely). When the leaving group is attached to a tertiary, allylic, or benzylic carbon, a carbocation intermediate will be relatively stable and thus an SN1 mechanism is favored.
2) The nucleophile: powerful nucleophiles, especially those with negative charges, favor the SN2 mechanism. Weaker nucleophiles such as water or alcohols favor the SN1 mechanism.
3) The solvent: Polar aprotic solvents favor the SN2 mechanism by enhancing the reactivity of the nucleophile. Polar protic solvents favor the SN1 mechanism by stabilizing the carbocation intermediate. SN1 reactions are frequently solvolysis reactions.
For example, the reaction below has a tertiary alkyl bromide as the electrophile, a weak nucleophile, and a polar protic solvent (we’ll assume that methanol is the solvent). Thus we’d confidently predict an SN1 reaction mechanism. Because substitution occurs at a chiral carbon, we can also predict that the reaction will proceed with racemization.

In the reaction below, on the other hand, the electrophile is a secondary alkyl bromide – with these, both SN1 and SN2 mechanisms are possible, depending on the nucleophile and the solvent. In this example, the nucleophile (a thiolate anion) is strong, and a polar protic solvent is used – so the SN2 mechanism is heavily favored. The reaction is expected to proceed with inversion of configuration.

Exercise 8.15: Determine whether each substitution reaction shown below is likely to proceed by an SN1 or SN2 mechanism.
In all of our discussion so far about nucleophilic substitutions, we have ignored another important possibility. In many cases, including the two examples above, substitution reactions compete with a type of reaction known as elimination. Consider, for example, the two courses that a reaction could take when tert-butyl bromide reacts with water:

We begin with formation of the carbocation intermediate. In pathway ‘a’, water acts as a nucleophile – this is, of course, the familiar SN1 reaction. However, a water molecule encountering the carbocation intermediate could alternatively act as a base rather than as a nucleophile, plucking a proton from one of the methyl carbons and causing the formation of a new carbon-carbon p bond. This alternative pathway is called an elimination reaction, and in fact with the conditions above, both the substitution and the elimination pathways will occur in competition with each other.
We will have lots more to say about elimination reactions in chapter 14, focusing on biochemical eliminations but also thinking about the competition between substitution and elimination that occurs with many nonenzymatic reactions.


