14.7: Titulaciones de ácido-base
- Page ID
- 1916
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Interpretar las curvas de valoración para sistemas de ácido-base fuertes y débiles
- Calcular el pH de la muestra en etapas importantes de una titulación
- Explicar la función de los indicadores de ácido-base
Como se vio en el capítulo sobre la estequiometría de las reacciones químicas, las titulaciones se pueden utilizar para analizar cuantitativamente las soluciones para sus concentraciones ácidas o básicas. En esta sección, examinaremos los cambios en las concentraciones de las especies ácidas y básicas presentes en una solución durante el proceso de la titulación.
Curvas de titulación
Anteriormente, cuando estudiamos las reacciones de ácido-base en solución, nos enfocamos solo en el punto en el que el ácido y la base eran estequiométricamente equivalentes. No tomamos en cuenta el pH de la solución antes, durante o después de la neutralización
Ejemplo \(\PageIndex{1}\): Cálculo del pH para soluciones de titulación: ácido fuerte/base fuerte
Se hace una titulación para 25.00 mL de HCl 0.100 M (ácido fuerte) con 0.100 M de una base fuerte, NaOH. La curva de titulación se muestra en la Figura \(\PageIndex{1}\). Calcule el pH a estos volúmenes de solución base agregada:
- 0.00 mL
- 12.50 mL
- 25.00 mL
- 37.50 mL
Solución
Ya que el HCl es un ácido fuerte, podemos asumir que todo se disocia. La concentración inicial de H3O+ es \(\ce{[H3O+] _ 0} = 0.100 \:M\). Cuando se agrega la solución base, también se disocia completamente, produciendo iones OH−. Los iones H3O+ y OH− se neutralizan entre sí, por lo que solo quedan los de los dos que estaban en exceso y su concentración determina el pH. Por tanto, la solución es inicialmente ácida (pH <7), pero eventualmente todos los iones hidronio presentes del ácido original se neutralizan y la solución se vuelve neutra. A medida que se agrega más base, la solución se vuelve básica.
La cantidad inicial total de iones hidronio es:
Ya que se agregen X mL de la solución base 0.100-M, la cantidad de moles de iones OH- presentes es:
El volumen total se hace:
\[V=\mathrm{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}\]
El número de moles de H3O+ se hace:
\[\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0=0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}\]
La concentración de H3O+ es:
\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{V}=\dfrac{0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}}\]
\[\mathrm{=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×X\: mL}{25.00\: mL+X\: mL}}\]
con la definición de \(\mathrm{pH}\):
\[\mathrm{pH=−\log([H_3O^+])} \label{phdef}\]
Los cálculos anteriores funcionan si \(\mathrm{n(H^+)_0-n(OH^-)_0>0}\) y entonces n(H+)> 0. Cuando \(\mathrm{n(H^+)_0=n(OH^-)_0}\), los iones H3O+ del ácido y los iones OH− de la base se neutralizan mutuamente. En este punto, los únicos iones de hidronio que quedan son los de la autoionización del agua, y no hay partículas de OH− para neutralizarlos. Por tanto, en este caso:
\[\ce{[H3O+]}=\ce{[OH- ]},\:\ce{[H3O+]}=K_\ce{w}=1.0\times 10^{-14};\:\ce{[H3O+]}=1.0\times 10^{-7}\]
\[\mathrm{pH=-log(1.0\times 10^{-7})=7.00}\]
Finalmente, cuando \(\mathrm{n(OH^-)_0>n(H^+)_0}\), no hay suficientes iones H3O+ para neutralizar todos los iones OH−, y en lugar de \(\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0}\), calculamos: \(\mathrm{n(OH^-)=n(OH^-)_0-n(H^+)_0}\)
En este caso:
\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)-0.002500\: mol}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}}\]
\[\mathrm{=\dfrac{0.100\:\mathit{M}×X\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+X\: mL}}\]
luego, usando la definición de \(pOH\) y su relación con el \(pH\) en soluciones acuosos a temperatura ambiente (Ecuación\ref{phdef}):
Consideremos ahora los cuatro casos específicos presentados en este problema:
(a) X = 0 mL
\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL}=0.1\:\mathit{M}}\]
luego usando la definición de \(pH\) (Equation \ref{phdef}):
\[\begin{align} pH &= −\log(0.100) \nonumber \\ &= 1.000 \nonumber\end{align} \]
(b) X = 12.50 mL
luego usando la definición de \(pH\) (Equation \ref{phdef}):
\[ \begin{align} pH &= −\log(0.0333) \nonumber \\ &= 1.477 \nonumber\end{align}\]
(c) X = 25.00 mL
Dado que los volúmenes y concentraciones de las soluciones ácida y básica son los mismos:
\[\mathrm{n(H^+)_0=n(OH^-)_0}\]
y
\[pH = 7.000\]
como describimos antes:
(d) X = 37.50 mL
En este caso:
\[\mathrm{n(OH^-)_0>n(H^+)_0} \]
luego usando la definición de \(pH\) (Equation \ref{phdef}):
\[ \begin{align}[pH = 14 − pOH \nonumber\\ &= 14 + \log([OH^{−}]) \nonumber \\ &= 14 + \log(0.0200) \nonumber \\ &= 12.30 \nonumber \end{align}\]
Ejercicio \(\PageIndex{1}\)
Calcule el pH para la titulación de ácido fuerte/base fuerte entre 50.0 mL de HNO3 0.100 M (aq) y NaOH 0.200 M (titulante) en los volúmenes listados de base agregada:
- 0.00 mL,
- 15.0 mL,
- 25.0 mL, y
- 40.0 mL.
- Respuesta a
-
0.00: 1.000
- Respuesta b
-
15.0: 1.5111
- Respuesta c
-
25.0: 7e. Do not delete this text first.
- Respuesta d
-
40.0: 12.523
En el Ejemplo \(\PageIndex{1}\), calculamos el pH en cuatro puntos durante una titulación. La tabla \(\PageIndex{1}\) muestra una secuencia detallada de cambios en el pH de un ácido fuerte y un ácido débil en una titulación con NaOH.
| Volumen de 0.100 M NaOH añadido (mL) | Moles de NaOH añadidos | Valores de pH de 0.100 M HCl1 | Valores de pH de 0.100 M \(CH_3CO_2H\)2 |
|---|---|---|---|
| 0.0 | 0.0 | 1.00 | 2.87 |
| 5.0 | 0.00050 | 1.18 | 4.14 |
| 10.0 | 0.00100 | 1.37 | 4.57 |
| 15.0 | 0.00150 | 1.60 | 4.92 |
| 20.0 | 0.00200 | 1.95 | 5.35 |
| 22.0 | 0.00220 | 2.20 | 5.61 |
| 24.0 | 0.00240 | 2.69 | 6.13 |
| 24.5 | 0.00245 | 3.00 | 6.44 |
| 24.9 | 0.00249 | 3.70 | 7.14 |
| 25.0 | 0.00250 | 7.00 | 8.72 |
| 25.1 | 0.00251 | 10.30 | 10.30 |
| 25.5 | 0.00255 | 11.00 | 11.00 |
| 26.0 | 0.00260 | 11.29 | 11.29 |
| 28.0 | 0.00280 | 11.75 | 11.75 |
| 30.0 | 0.00300 | 11.96 | 11.96 |
| 35.0 | 0.00350 | 12.22 | 12.22 |
| 40.0 | 0.00400 | 12.36 | 12.36 |
| 45.0 | 0.00450 | 12.46 | 12.46 |
| 50.0 | 0.00500 | 12.52 | 12.52 |
|
|||
Las reacciones ácido-base más simples son las de un ácido fuerte con una base fuerte. La tabla \(\PageIndex{1}\) muestra los datos para la titulación de una muestra de 25.0 mL de ácido clorhídrico 0.100 M con hidróxido de sodio de concentración 0.100 M. Los valores del pH medidos después de adiciones sucesivas de pequeñas cantidades de NaOH se listan en la primera columna de esta tabla y se representan en la Figura \(\PageIndex{1}\), en una forma que se llama la curva de titulación. El pH aumenta lentamente al principio, aumenta rápidamente en la parte media de la curva y luego aumenta lentamente nuevamente. El punto de inflexión (ubicado en el punto medio de la parte vertical de la curva) es el punto de equivalencia para la titulación. Indica cuando están presentes cantidades equivalentes de ácido y base. Para la titulación de un ácido fuerte con una base fuerte, el punto de equivalencia ocurre a un pH de 7.00 y los puntos de la curva de titulación se pueden calcular utilizando estequiometría en solución (Tabla \(\PageIndex{1}\) y Figura \(\PageIndex{1}\)).
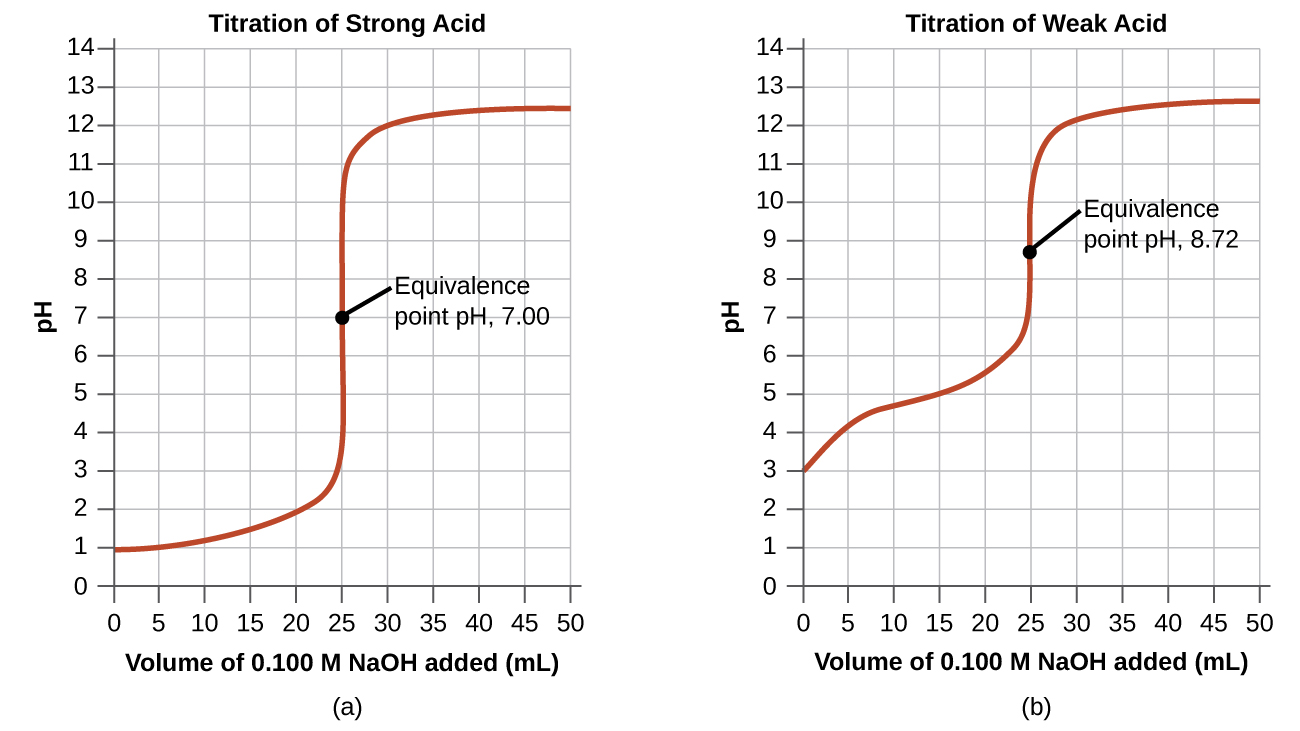
La valoración de un ácido débil con una base fuerte (o de una base débil con un ácido fuerte) es algo más complicada que la que se acaba de discutir, pero sigue los mismos principios generales. Consideremos la titulación de 25.0 mL de ácido acético 0.100 M (un ácido débil) con hidróxido de sodio 0.100 M y compare la curva de titulación con la del ácido fuerte. La tabla \(\PageIndex{1}\) muestra los valores de pH durante la titulación, la figura \(\PageIndex{1b}\) muestra la curva de titulación.
Aunque el volumen inicial y la molaridad de los ácidos son los mismos, existen diferencias importantes entre las dos curvas de titulación. La curva de titulación para el ácido débil comienza con un valor más alto (menos ácido) y mantiene valores de pH más altos hasta el punto de equivalencia. Esto se debe a que el ácido acético es un ácido débil, que está solo parcialmente ionizado. El pH en el punto de equivalencia también es más alto (8.72 en lugar de 7.00) debido a la hidrólisis del acetato, una base débil que eleva el pH:
Después del punto de equivalencia, las dos curvas son idénticas porque el pH depende del exceso de ion hidróxido en ambos casos.
Ejemplo (\PageIndex{2}\): Valoración de un ácido débil con una base fuerte
La curva de titulación que se muestra en la Figura \(\PageIndex{1b}\) es para la titulación de 25.00 mL de CH3CO2H 0.100 M con 0.100 M NaOH. La reacción se puede representar como:
\[\ce{CH3CO2H + OH- ⟶ CH3CO2- + H2O}\]
- ¿Cuál es el pH inicial antes de agregar cualquier cantidad de la solución de NaOH? Ka = 1.8 × 10−5 para CH3CO2H.
- Encuentre el pH después de agregar 25.00 mL de la solución de NaOH.
- Encuentre el pH después de agregar 12.50 mL de la solución de NaOH.
- Encuentre el pH después de agregar 37.50 mL de la solución de NaOH.
Solución
(a) Suponiendo que la cantidad disociada es pequeña en comparación con 0.100 M, encontramos que:
\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}≈\ce{\dfrac{[H3O+]^2}{[CH3CO2H]_0}}\]
y
\[\ce{[H3O+]}=\sqrt{K_\ce{a}×\ce{[CH3CO2H]}}=\sqrt{1.8\times 10^{-5}×0.100}=1.3\times 10^{-3}\]
(b) Después de agregar 25.00 mL de NaOH, el número de moles de NaOH y CH3CO2H es igual porque las cantidades de las soluciones y sus concentraciones son las mismas. Todo el CH3CO2H se ha convertido en \(\ce{CH3CO2-}\). La concentración del ion \(\ce{CH3CO2-}\) es:
El equilibrio en el que nos debemos enfocar ahora es la constante de basicidad para \(\ce{CH3CO2-}\):
así que debemos determinar Kb para la base usando la constante del producto iónico para el agua:
\[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}}\]
Ya que Kw = [H+][OH−]:
Denotemos la concentración de cada unTenga en cuenta que el pH en el punto de equivalencia de esta titulación es significativamente más grande que 7.o de los productos de esta reacción, CH3CO2H y OH−, como x. Usando la suposición que x es pequeño en comparación con 0.0500 M, \(K_\ce{b}=\dfrac{x^2}{0.0500\:M}\), y luego:
Tenga en cuenta que el pH en el punto de equivalencia de esta titulación es significativamente más grande que 7.
(c) En (a), se agregaron 25.00 mL de la solución de NaOH, por eso prácticamente todo el CH3CO2H se convirtió en \(\ce{CH3CO2-}\). En este caso, solo se han introducido 12.50 mL de la solución base, por eso solo la mitad de todo el CH3CO2H se convierte en \(\ce{CH3CO2-}\). El número inicial total de moles de CH3CO2H es 0.02500L × 0.100 M = 0.00250 mol, por eso después de agregar el NaOH, el número de moles de CH3CO2H y \(\ce{CH3CO2-}\) son aproximadamente iguales a \(\mathrm{\dfrac{0.00250\:mol}{2}=0.00125\:mol}\), y sus concentraciones son las mismas.
Dado que la cantidad de base agregada es menor que la cantidad original de ácido, no se ha alcanzado el punto de equivalencia, la solución permanece un amortiguador y podemos usar la ecuación de Henderson-Hasselbalch:
(como las concentraciones de \(\ce{CH3CO2-}\) y CH3CO2H son iguales)
Así:
(el pH = el pKa en el punto medio en una titulación de un ácido débil)
(d) Después de agregar 37.50 ml de NaOH, la cantidad de NaOH es 0.03750 L x 0.100 M = 0.003750 mol de NaOH. Dado que esto ha superado el punto de equivalencia, el exceso de iones de hidróxido hará que la solución sea básica, y podemos otra vez usar cálculos estequiométricos para determinar el pH:
Entonces:
Tenga en cuenta que este resultado es el mismo que para el ejemplo de valoración de ácido fuerte-base fuerte dada anteriormente, ya que la cantidad de base fuerte añadida causa que la solución esté más allá del punto de la equivalencia.
Ejercicio \(\PageIndex{2}\)
Calcule el pH para la titulación de ácido débil/base fuerte entre 50.0 mL de 0.100 M HCOOH(aq) (ácido fórmico) y 0.200 M NaOH (titrante) a los volúmenes listados de base agregado:
- 0.00 mL,
- 15.0 mL,
- 25.0 mL, y
- 30.0 mL.
- Respuesta a
-
0.00 mL: 2.37
- Respuesta b
-
15.0 mL: 3.92
- Respuesta c
-
25.00 mL: 8.29
- Respuesta d
-
30.0 mL: 12.097
Indicadores de ácido-base
Ciertas sustancias orgánicas cambian de color en una solución diluida cuando la concentración de iones hidronio alcanza un valor particular. Por ejemplo, la fenolftaleína es una sustancia incolora en cualquier solución acuosa con una concentración de iones hidronio más grande que 5.0 × 10−9 M (pH <8.3). En soluciones más básicas donde la concentración de iones hidronio es menos que 5.0 × 10−9 M (pH> 8.3), es rojo o rosado. Las sustancias como la fenolftaleína, que se pueden utilizar para determinar el pH de una solución, se llaman indicadores de ácido-base. Los indicadores ácido-base son ácidos orgánicos débiles o bases orgánicas débiles.
El equilibrio en una solución del indicador ácido-base naranja de metilo, un ácido débil, se puede representar por una ecuación en la que usamos \(\ce{HIn}\) como una representación simple de la molécula compleja de naranja de metilo:
\[\underbrace{\ce{HIn (aq)}}_{\ce{red}}+\ce{H2O (l)}⇌\ce{H3O^{+} (aq)}+\underbrace{\ce{In^{-} (aq)}}_{\ce{yellow}}\]
\[K_\ce{a}=\ce{\dfrac{[H3O+][In- ]}{[HIn]}}=4.0\times 10^{−4}\]
El anión de naranja de metilo, \(\ce{In^{-}\), es amarillo, y la forma no ionizada, \(\ce{HIn}\), es roja. Cuando agregamos ácido a una solución de naranja de metilo, el aumento de la concentración de iones hidronio desplaza el equilibrio hacia la forma roja no ionizada, de acuerdo con el principio de Le Chatelier. Si agregamos base, cambiamos el equilibrio hacia la forma amarilla. Este comportamiento es completamente análogo a la acción de los búferes.
El color de un indicador es el resultado visible de la relación de las concentraciones de las dos especies ln− y \(\ce{HIn}\). Si la mayor parte del indicador (típicamente alrededor del 60-90% o más) está presente como \(\ce{In^{-}\), entonces vemos el color del ion \(\ce{In^{-}\), que sería amarillo para el naranja de metilo. Si la mayoría parte del indicador está presente como \(\ce{HIn}\), entonces vemos el color de la molécula \(\ce{HIn}\): rojo para el naranja de metilo. Para el naranja de metilo, podemos reorganizar la ecuación de Ka y escribir:
\[\mathrm{\dfrac{[In^-]}{[HIn]}=\dfrac{[substance\: with\: yellow\: color]}{[substance\: with\: red\: color]}=\dfrac{\mathit{K}_a}{[H_3O^+]}} \label{ABeq2}\]
La ecuación \ref{ABeq2} nos muestra cómo varía la proporción de \(\ce{\dfrac{[In-]}{[HIn]}}\) con la concentración de ion hidronio. La expresión anterior que describe el equilibrio del indicador se puede reorganizar:
\[ \begin{align} \dfrac{[H_3O^+]}{\mathit{K}_a} &=\dfrac{[HIn]}{[In^- ]} \\[8pt] \log\left(\dfrac{[H_3O^+]}{\mathit{K}_a}\right) &= \log\left(\dfrac{[HIn]}{[In^- ]}\right) \\[8pt] \log([H_3O^+])-\log(\mathit{K}_a) &=-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] -pH+p\mathit{K}_a & =-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] pH &=p\mathit{K}_a+\log\left(\dfrac{[In^-]}{[HIn]}\right) \end {align}\]
o en términos generales
\[pH=p\mathit{K}_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{HHeq} \]
La ecuación \ref{HHeq} es la misma que la ecuación de Henderson-Hasselbalch, que se puede utilizar para describir el equilibrio de indicadores.
Cuando [H3O+] tiene el mismo valor numérico que Ka, la relación de [ln−] a [Hln] es igual a 1, lo que significa que el 50% del indicador está presente en la forma roja (Hln) y el 50% está en la forma iónica amarilla (ln-), y la solución aparece de color naranja. Cuando la concentración de iones hidronio aumenta a 8 × 10−4 M (un pH de 3.1), la solución se vuelve roja. No es visible ningún cambio de color por cualquier aumento adicional en la concentración de iones hidronio (disminución del pH). A una concentración de iones de hidronio de 4 × 10−5 M (un pH de 4.4), la mayor parte del indicador se encuentra en la forma iónica amarilla, y una disminución adicional en la concentración de iones de hidronio (aumento del pH) no produce un cambio en el color visible. El rango de pH entre 3.1 (rojo) y 4.4 (amarillo) es el intervalo de cambio de color del naranja de metilo; el cambio de color pronunciado tiene lugar entre estos valores de pH.
Hay muchos diferentes indicadores de ácido-base que cubren un amplio rango de valores de pH y se pueden usar para determinar el pH aproximado de una solución desconocida mediante un proceso de eliminación. Los indicadores universales y el papel de pH contienen una mezcla de indicadores y exhiben diferentes colores a diferentes pH. La Figura \(\PageIndex{2}\) presenta varios indicadores, sus colores y sus intervalos de cambio de color.
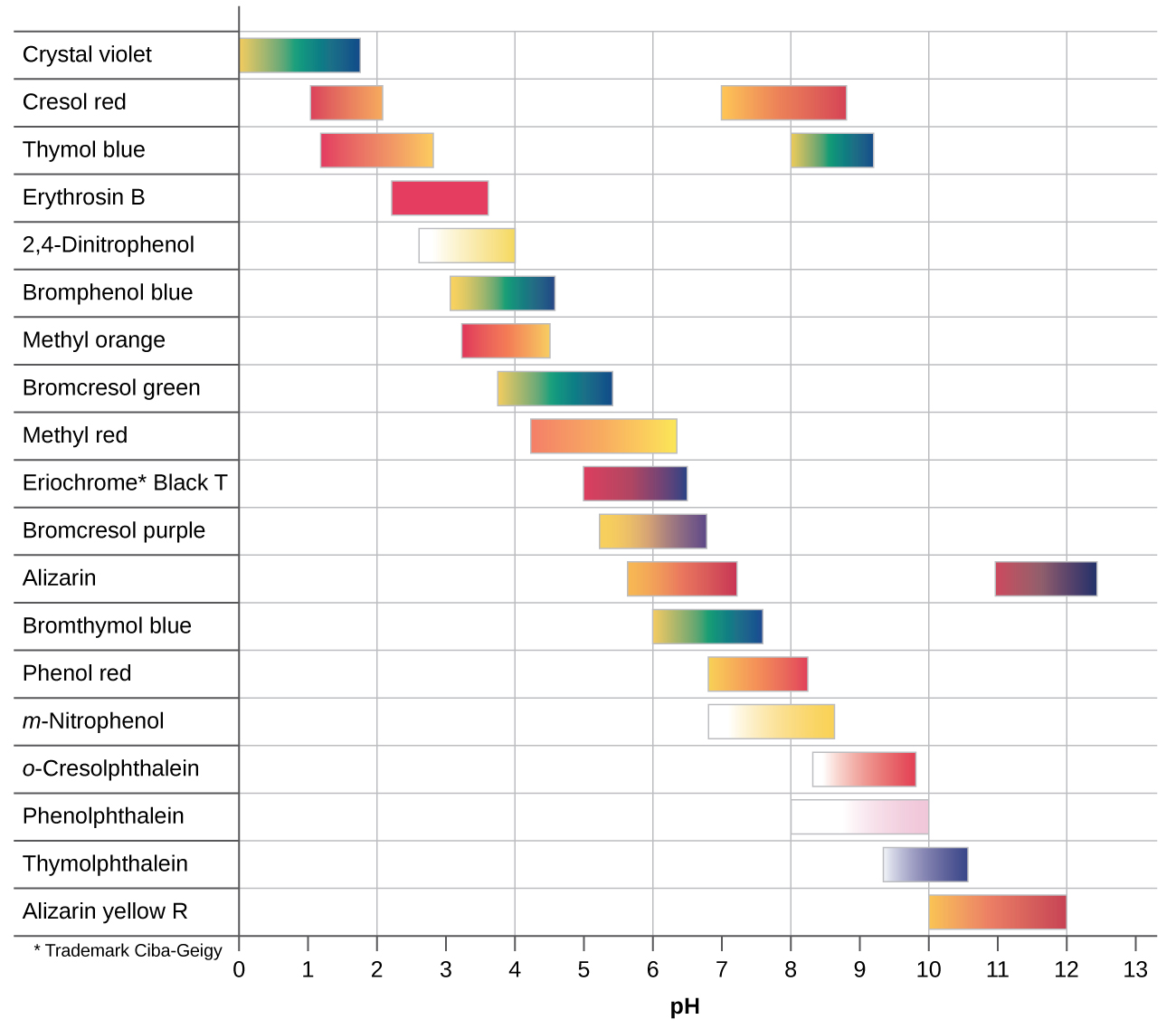
Las curvas de valoración nos ayudan a elegir un indicador que nos dará un cambio de color fuerte en el punto de equivalencia. La mejor selección sería un indicador que tenga un intervalo de cambio de color que incluya el pH en el punto de equivalencia de la titulación.
Los intervalos de cambio de color de tres indicadores se muestran en la Figura \(\PageIndex{3}\). Los puntos de equivalencia tanto de la titulación del ácido fuerte como del ácido débil se encuentran en el intervalo de cambio de color de la fenolftaleína. Podemos usarlo para valoraciones de ácido fuerte con base fuerte o ácido débil con base fuerte.
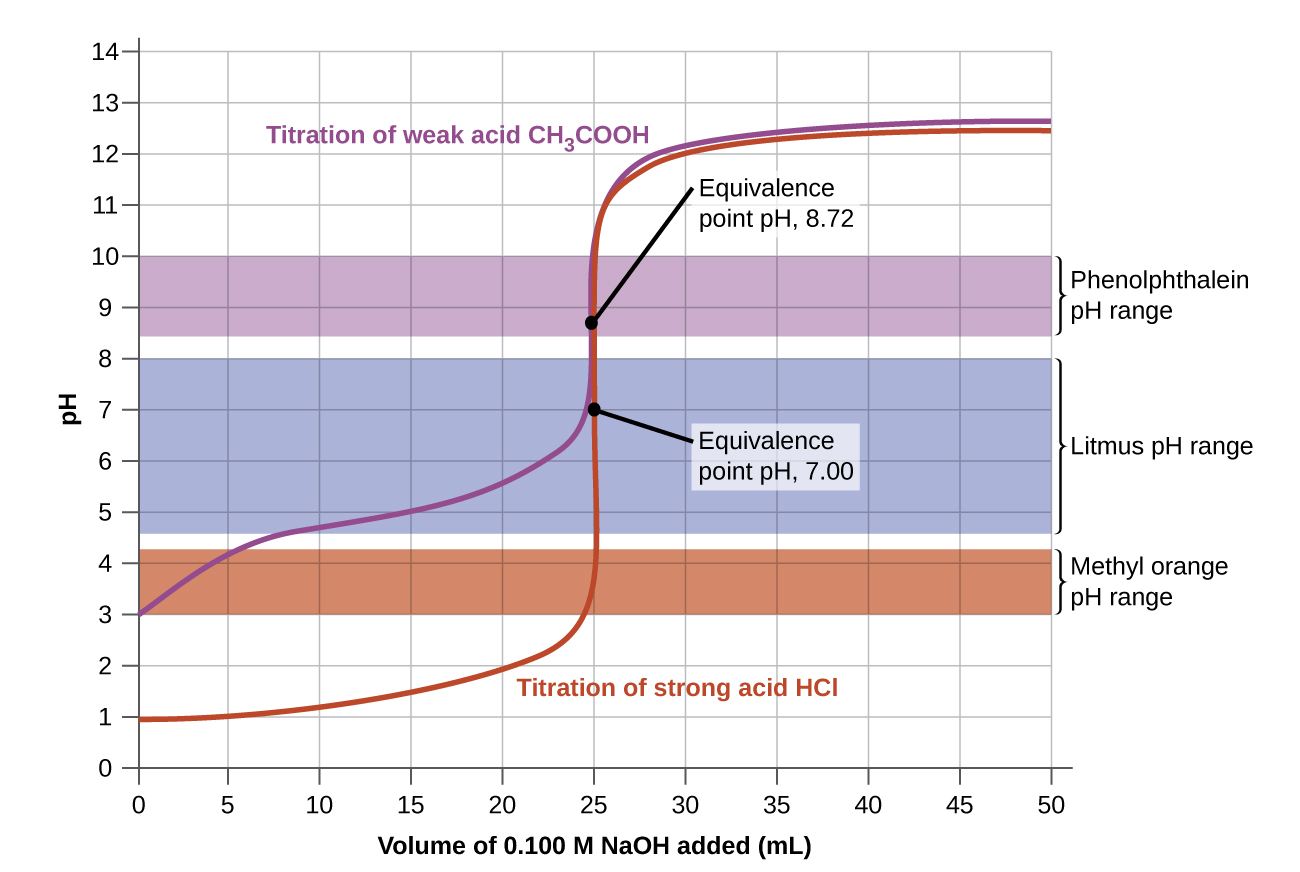
El tornasol es un indicador adecuado para la titulación de HCl porque su cambio de color marca el punto de equivalencia. Sin embargo, no debemos usar el tornasol para la titulación de CH3CO2H porque el pH está dentro del intervalo de cambio de color del tornasol cuando solo se han agregado unos 12 ml de NaOH, y no sale del rango hasta que se han agregado 25 ml. El cambio de color sería muy gradual, ocurriendo durante la adición de 13 mL de NaOH, haciendo que el tornasol inservible como el indicador del punto de equivalencia.
Podríamos usar el naranja de metilo para la titulación de HCl, pero no nos daría resultados muy precisos: (1) Completa su cambio de color un poco antes de que se alcance el punto de equivalencia (pero muy cerca de él, por lo que esto no es demasiado serio); (2) cambia de color, como demuestra la Figura \(\PageIndex{2}\), durante la adición de casi 0.5 ml de NaOH, que no es un cambio de color tan fuerte como el del tornasol o la fenolftaleína; y (3) pasa de amarillo a naranja a rojo, lo que hace que la detección de un punto final preciso sea mucho más desafiante que el cambio de incoloro a rosado de la fenolftaleína. La Figura \(\PageIndex{2}\) nos muestra que el naranja de metilo sería completamente inútil como un indicador para la titulación de CH3CO2H. Su cambio de color comienza después de agregar aproximadamente 1 ml de NaOH y finaliza cuando se agregan aproximadamente 8 ml de NaOH. El cambio de color se completa mucho antes de que se alcance el punto de equivalencia (que se produce cuando se han añadido 25.0 ml de NaOH) y, por tanto, no nos da ninguna indicación del punto de equivalencia.
Basamos nuestra elección de indicador en un pH calculado, el pH en el punto de equivalencia. En el punto de equivalencia, se han mezclado cantidades equimolares de ácido y base, y el cálculo se convierte en el del pH de una solución de la sal resultante de la titulación.
Resumen
Una curva de titulación es un gráfico que relaciona el cambio de pH de una solución ácida o básica con el volumen de titulador añadido. Las características de la curva de titulación dependen de las soluciones específicas que se titulan. El pH de la solución en el punto de equivalencia puede ser mayor, igual o menos que 7.00. La elección de un indicador para una titulación determinada depende del pH esperado en el punto de equivalencia de la titulación y del rango de cambio de color del indicador.
Glosario
- indicador ácido-base
- Ácido orgánico o base que cambia color según el pH de la solución en la que se encuentra
- intervalo de cambio de color
- rango de pH en el que se produce el cambio de color de un indicador
- curva de titulación
- gráfico del pH de una solución de ácido o base frente al volumen de base o ácido añadido durante una titulación
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


