14.6: Las soluciones tampón

Habilidades para desarrollar

• Describir la composición y función de los tampones de ácido-base.
• Calcule el pH de un tampón antes y después de la adición de ácido o base

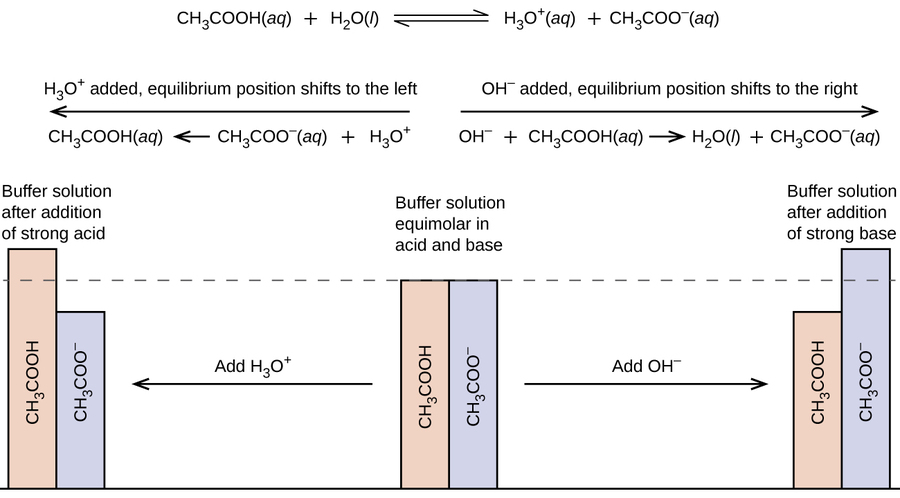
Una mezcla de un ácido débil y su base conjugada (o una mezcla de una base débil y su ácido conjugado) se llama una solución tampón o un tampón. Las soluciones tampón resisten un cambio en el pH cuando se agregan pequeñas cantidades de un ácido fuerte o una base fuerte (Figura \(\PageIndex{1}\)). Una solución de ácido acético (\(\ce{CH3COOH}\) y acetato de sodio \(\ce{CH3COONa}\)) es un ejemplo de un tampón que consiste en un ácido débil y su sal. Un ejemplo de un tampón que consiste en una base débil y su sal es una solución de amoníaco (\(\ce{NH3(aq)}\)) y cloruro de amonio (\(\ce{NH4Cl(aq)}\)). Calcule el pH de un tampón antes y después de la adición de ácido o base.

Figura \(\PageIndex{1}\): (a) La solución tampón de la izquierda y la solución sin tampón de la derecha tienen el mismo pH (pH 8); son soluciones básicas y muestran el color amarillo del indicador naranja de metilo a este pH. (b) Después de la adición de 1 ml de una solución de HCl 0.01-M, la solución sin tampón no ha cambiado su pH de manera detectable, pero la solución sin tampón se ha vuelto ácida, como lo indica el cambio de color de la naranja de metilo, que se vuelve roja en un pH de aproximadamente 4. (crédito: modificación del trabajo de Mark Ott)

Como funcionan los tampones

Una mezcla de ácido acético y acetato de sodio es ácida porque el K_a del ácido acético es más grande que el K_b de su acetato base conjugado. Es un tampón porque contiene tanto el ácido débil como su sal. Por lo tanto, actúa para mantener la concentración de los iones de hidronio (y el pH) casi constante mediante la adición de una pequeña cantidad de un ácido fuerte o una base fuerte. Si agregamos una base como el hidróxido de sodio, los iones de hidróxido reaccionan con los pocos iones de hidronio presentes. Luego, más ácido acético reacciona con el agua, restaurando la concentración de los iones hidronio casi a su valor original:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)\]

El pH cambia muy poco. Si agregamos un ácido como el ácido clorhídrico, la mayoría de los iones hidronio del ácido clorhídrico se combinan con iones acetato, formando moléculas de ácido acético:

\[\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)⟶\ce{CH3CO2H}(aq)+\ce{H2O}(l)\]

Por lo tanto, hay muy poco aumento en la concentración del ion hidronio, y el pH permanece prácticamente sin cambios (Figura \(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Este diagrama muestra la acción amortiguadora de estas reacciones.

Una mezcla de amoníaco y cloruro de amonio es básica porque el Kb para el amoníaco es más grande que el Ka para el ion de amonio. Es un tampón porque también contiene la sal de la base débil. Si agregamos una base (iones de hidróxido), los iones de amonio en el tampón reaccionan con los iones de hidróxido para formar el amoníaco y el agua y reducen la concentración de los iones de hidróxido casi a su valor original:

\[\ce{NH4+}(aq)+\ce{OH-}(aq)⟶\ce{NH3}(aq)+\ce{H2O}(l)\]

Si agregamos un ácido (iones de hidronio), las moléculas de amoníaco en la mezcla tampón reaccionan con los iones de hidronio para formar iones de amonio y reducen la concentración de los iones de hidronio casi a su valor original:

\[\ce{H3O+}(aq)+\ce{NH3}(aq)⟶\ce{NH4+}(aq)+\ce{H2O}(l)\]

Las tres partes del siguiente ejemplo ilustran el cambio en el pH que acompaña la adición de una base a una solución con tampón de un ácido débil y a una solución sin tampón de un ácido fuerte.

Ejemplo \(\PageIndex{1}\): Cambios de pH en soluciones con tampón y sin tampón

Los tampones de acetato se usan en estudios bioquímicos de enzimas y otros componentes químicos de las células para prevenir los cambios de pH que podrían cambiar la actividad bioquímica de estos compuestos.

a. Calcule el pH de un tampón de acetato que es una mezcla con ácido acético 0.10 M y acetato de sodio 0.10 M.

b. Calcule el pH después de agregar 1.0 mL de NaOH 0.10 M a 100 mL de este tampón, dando una solución con un volumen de 101 mL.

Solución

1. Calcule el pH de un tampón de acetato que es una mezcla con ácido acético 0.10 M y acetato de sodio 0.10 M.

   Para determinar el pH de la solución tampón, usamos un cálculo de equilibrio típico (como se ilustra en los ejemplos anteriores):

   

   1. Determine la dirección del cambio. El equilibrio en una mezcla de H₃O⁺, \(\ce{CH3CO2-}\) y CH₃CO₂H es:

      \[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber\]

La constante de equilibrio para CH₃CO₂H no se da, por eso la buscamos en Tabla E1: K_a = 1.8 × 10⁻⁵. Con [CH₃CO₂H] = \(\ce{[CH3CO2- ]}\) = 0.10 M y [H₃O⁺] = ~0 M, la reacción se desplaza hacia la derecha para formar H₃O⁺.

Determine x y las concentraciones de equilibrio. A continuación puedes ver una tabla de cambios y concentraciones:

Resuelve para x y las concentraciones de equilibrio. Encontramos que:

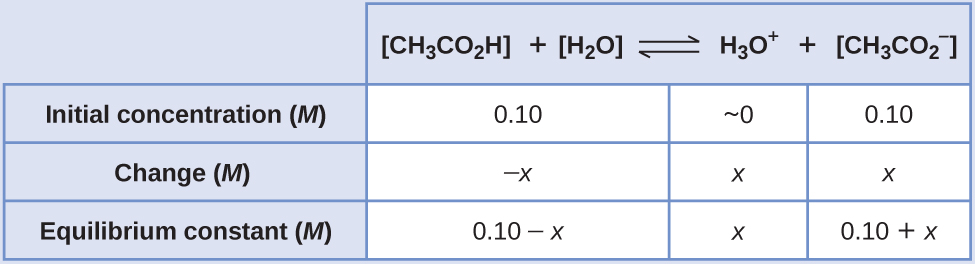
\[x=1.8×10^{−5}\:M\]

y

\[\ce{[H3O+]}=0+x=1.8×10^{−5}\:M\]

Así:

\[\mathrm{pH=−log[H_3O^+]=−log(1.8×10^{−5})}\]

\[=4.74\]

• Revise su trabajo. Si calculamos todas las concentraciones de equilibrio calculadas, encontramos que el valor de equilibrio del coeficiente de reacción, Q = K_a.

(b) Calcule el pH después de agregar 1.0 mL de NaOH 0.10 M a 100 mL de este tampón, dando una solución con un volumen de 101 mL.

Primero, calculamos las concentraciones de una mezcla intermedia resultante de la reacción completa entre el ácido en el tampón y la base añadida. Luego determinamos las concentraciones de la mezcla en el nuevo equilibrio:

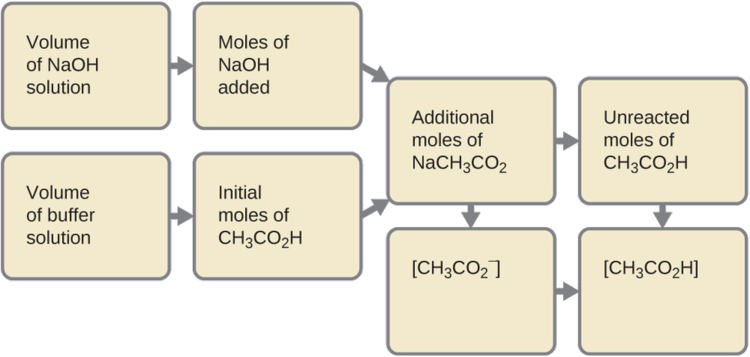
1. Determine los moles de NaOH. Un mililitro (0.0010 L) de 0.10 M NaOH contiene:

   \[\mathrm{0.0010\cancel{L}×\left(\dfrac{0.10\:mol\: NaOH}{1\cancel{L}}\right)=1.0×10^{−4}\:mol\: NaOH} \nonumber\]

2. Determine los moles de CH₂CO₂H. Antes de la reacción, 0.100 L de la solución de tampón contiene:

   \[\mathrm{0.100\cancel{L}×\left(\dfrac{0.100\:mol\:CH_3CO_2H}{1\cancel{L}}\right)=1.00×10^{−2}\:mol\:CH_3CO_2H} \nonumber\]

3. Resuelva para la cantiEncuentre la molaridad de los productos. Después de la reacción, CH3CO2H y NaCH3CO2 están contenidos en 101 ml de la solución intermedia, entonces:dad de NaCH₃CO₂ producida por la reacción. El 1.0 × 10⁻⁴ mol de NaOH neutraliza 1.0 × 10⁻⁴ mol de CH₃CO₂H, dejando:

   \[\mathrm{(1.0×10^{−2})−(0.01×10^{−2})=0.99×10^{−2}\:mol\:CH_3CO_2H}\nonumber\]

   y produciendo 1.0 × 10⁻⁴ mol de NaCH₃CO₂. Esto nos da un total de:

\[\mathrm{(1.0×10^{−2})+(0.01×10^{−2})=1.01×10^{−2}\:mol\:NaCH_3CO_2}\nonumber\]

• Encuentre la molaridad de los productos. Después de la reacción, CH₃CO₂H y NaCH₃CO₂ están contenidos en 101 ml de la solución intermedia, entonces:
  \[\ce{[CH3CO2H]}=\mathrm{\dfrac{9.9×10^{−3}\:mol}{0.101\:L}}=0.098\:M\nonumber\]

  \[\ce{[NaCH3CO2]}=\mathrm{\dfrac{1.01×10^{−2}\:mol}{0.101\:L}}=0.100\:M\nonumber\]

  Ahora calculamos el pH después de que la solución intermedia, que es 0.098 M en CH₃CO₂H y 0.100 M en NaCH₃CO₂, llega al equilibrio. El cálculo es muy similar al de la parte (a) de este ejemplo:

  

  Esta serie de cálculos da un pH = 4.75. Por lo tanto, la adición de la base cambia el pH de la solución solo un poco.

(c) Para comparación, calcule el pH después de agregar 1.0 mL de NaOH 0.10 M a 100 mL de una solución de una solución sin tampón con un pH de 4.74 (una solución de HCl 1.8 × 10−5-M). El volumen de la solución final es de 101 ml.

Solución

Esta solución de HCl 1.8 × 10⁻⁵-M tiene la misma concentración de iones de hidronio que la solución conteniendo 0.10-M de tampón de ácido acético-acetato de sodio descrito en la parte (a) de este ejemplo. La solución contiene:

\(\mathrm{0.100\:L×\left(\dfrac{1.8×10^{−5}\:mol\: HCl}{1\:L}\right)=1.8×10^{−6}\:mol\: HCl}\nonumber\)

Como se muestra en la parte (b), 1 ml de NaOH 0.10 M contiene 1.0 × 10⁻⁴ mol de NaOH. Cuando las soluciones de NaOH y HCl se mezclan, el HCl es el reactivo limitante en la reacción. Todo el HCl reacciona, y la cantidad de NaOH que queda es:

\( (1.0×10^{−4})−(1.8×10^{−6})=9.8×10^{−5}\:M\nonumber\)

La concentracion de NaOH es:

\(\dfrac{9.8×10^{−5}\:M\:\ce{NaOH}}{0.101\:\ce{L}}=9.7×10^{−4}\:M\nonumber\)

El pOH de la solución es:

\(\mathrm{pOH=−log[OH^- ]=−log(9.7×10^{−4})=3.01}\nonumber\)

El pH es:

\(\mathrm{pH=14.00−pOH=10.99}\nonumber\)

El pH cambia de 4.74 a 10.99 en esta solución sin tampón. Esto se compara con el cambio de 4.74 a 4.75 que ocurrió cuando se añadió la misma cantidad de NaOH a la solución con tampón descrita en parte (b).

Ejercicio \(\PageIndex{1}\)

Muestre que la adición de 1.0 mL de HCl 0.10 M cambia el pH de 100 mL de una solución de HCl 1.8 × 10⁻⁵ M de 4.74 a 3.00.

Respuesta

pH inicial de 1.8 × 10⁻⁵ M HCl; pH = −log[H₃O⁺] = −log[1.8 × 10⁻⁵] = 4.74

Moles de H₃O⁺ agregados por la adicion de 1.0 mL de 0.10 M HCl: 0.10 moles/L × 0.0010 L = 1.0 × 10⁻⁴ moles; pH final despues de agregar 1.0 mL de 0.10 M HCl:

\[\mathrm{pH=−log[H_3O^+]=−log\left(\dfrac{total\: moles\:H_3O^+}{total\: volume}\right)=−log\left(\dfrac{1.0×10^{−4}\:mol+1.8×10^{−6}\:mol}{101\:mL\left(\dfrac{1\:L}{1000\:mL}\right)}\right)=3.00}\nonumber\]

Capacidad del tampón

Las soluciones tampón no tienen una capacidad sin límites para mantener el pH relativamente constante (Figura \(\PageIndex{3}\)). Si agregamos tanta base a un tampón que el ácido débil que se acaba no es posible más acción de amortiguación hacia la base. Por otro lado, si agregamos un exceso de ácido, la base débil se acabaría y no sería posible una acción de amortiguación hacia ningún ácido adicional. De hecho, ni siquiera necesitamos acabar todo el ácido o la base en un tampón para superarlo; su acción amortiguadora disminuirá rápidamente a medida que un componente dado se acerque al agotamiento.

Figura \(\PageIndex{3}\): El color del indicador (naranja de metilo) muestra que una pequeña cantidad de ácido agregado a una solución con tampón de pH 8 (vaso de precipitados a la izquierda) tiene poco efecto en el sistema tamponado (vaso de precipitados a la derecha). Sin embargo, una gran cantidad de ácido agota la capacidad de amortiguación de la solución y el pH cambia dramáticamente (vaso de precipitados a la derecha). (crédito: modificación del trabajo de Mark Ott)

La capacidad del tampón es la cantidad de ácido o base que se puede agregar a un volumen dado de una solución tampón antes de que el pH cambie significativamente, generalmente en una unidad. La capacidad del tampón depende de las cantidades del ácido débil y su base conjugada que se encuentran en una mezcla de tampón. Por ejemplo, 1 L de una solución que es 1.0 M en ácido acético y 1.0 M en acetato de sodio tiene una capacidad de tampón mayor que 1 L de una solución que es 0.10 M en ácido acético y 0.10 M en acetato de sodio a pesar de que ambas soluciones tienen el mismo pH. La primera solución tiene más capacidad de tampón porque contiene más ácido acético e ion acetato.

Selección de mezclas de tampón adecuadas

Existen dos reglas prácticas para seleccionar mezclas de tampones:

1. Una buena mezcla tampón debe tener concentraciones aproximadamente iguales de sus dos componentes. Una solución tampón generalmente ha perdido su utilidad cuando un componente del par de tampones es inferior a aproximadamente el 10% del otro. La figura \(\PageIndex{4}\) muestra un tampón iónico de ácido acético-acetato a medida que se agrega la base. El pH inicial es 4.74. Se produce un cambio de 1 unidad de pH cuando la concentración de ácido acético se reduce al 11% de la concentración de iones acetato.

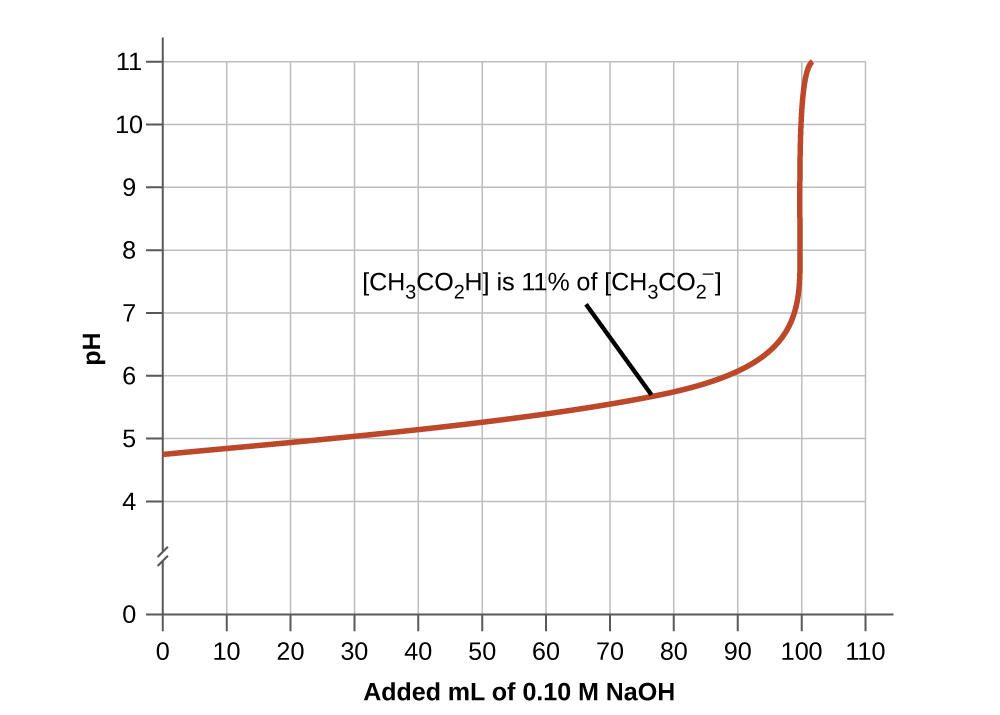
Figura \(\PageIndex{4}\): El gráfico, una ilustración de la acción de amortiguación, muestra el cambio de pH a medida que se agrega una cantidad creciente de una solución de NaOH 0.10-M a 100 ml de una solución amortiguadora en la cual, inicialmente, [CH₃CO₂H] = 0.10 M y \(\ce{[CH3CO2-]} = 0.10 \:M\).

2. Los ácidos débiles y sus sales son mejores como amortiguadores para pH inferiores a 7; las bases débiles y sus sales son mejores como amortiguadores para pH más grade que 7.

La sangre es un ejemplo importante de una solución tamponada, con el principal ácido e ión responsable de la acción amortiguadora que es el ácido carbónico, H2CO3, y el ion bicarbonato, \(\ce{HCO3-}\). Cuando un exceso de iones de hidrógeno ingresa al torrente sanguíneo, se elimina principalmente por la reacción:

\[\ce{H3O+}(aq)+\ce{HCO3-}(aq)⟶\ce{H2CO3}(aq)+\ce{H2O}(l)\]

Cuando hay un exceso del ion hidróxido, se elimina por la reacción:

\[\ce{OH-}(aq)+\ce{H2CO3}(aq)⟶\ce{HCO3-}(aq)+\ce{H2O}(l)\]

El pH de la sangre humana, por lo tanto, permanece muy cerca de 7.35, es decir, un poco básica. Las variaciones son generalmente menos de 0.1 de una unidad de pH. Es probable que un cambio de 0.4 de una unidad de pH sea fatal.

La aproximación de Henderson-Hasselbalch

La expresión de ionización constante para una solución de un ácido débil se puede escribir como:

\[K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\]

Al reorganizar para resolver [H₃O⁺], obtenemos:

\[\ce{[H3O+]}=K_\ce{a}×\ce{\dfrac{[HA]}{[A- ]}}\]

Tomando el logaritmo negativo de ambos lados de esta ecuación nos da:

\[\mathrm{−log[H_3O^+]=−log\mathit{K}_a − log\dfrac{[HA]}{[A^- ]}}\]

que se puede escribir como:

\[\mathrm{pH=p\mathit{K}_a+log\dfrac{[A^- ]}{[HA]}}\]

donde pK_a es el negativo del logaritmo común de la constante de ionización del ácido débil (pK_a = −log K_a). Esta ecuación relaciona el pH, la constante de ionización de un ácido débil y las concentraciones del ácido débil y su sal en una solución tamponada. A veces, los científicos usan esta expresión, llamada la aproximación de Henderson-Hasselbalch, para calcular el pH de las soluciones de tampón. Es importante tener en cuenta que la suposición "x es pequeña" debe ser válida para usar esta ecuación.

Lawrence Joseph Henderson y Karl Albert Hasselbalch

Lawrence Joseph Henderson (1878–1942) fue un médico, bioquímico y fisiólogo estadounidense, por nombrar solo algunas de sus muchas actividades. Obtuvo un título de médico en Harvard y luego pasó 2 años estudiando en Estrasburgo, luego parte de Alemania, antes de regresar para tomar un puesto de profesor en Harvard. Eventualmente se convirtió en profesor en Harvard y trabajó allí toda su vida. Descubrió que el equilibrio ácido-base en la sangre humana está regulado por un sistema tampón formado por el dióxido de carbono disuelto en la sangre. Escribió una ecuación en 1908 para describir el sistema tampón de ácido carbónico y carbonato en la sangre. Henderson estaba ampliamente informado; además de su importante investigación sobre la fisiología de la sangre, también escribió sobre las adaptaciones de los organismos y sus ajustes en sus entornos, sobre la sociología y la educación universitaria. También fundó el Fatigue Laboratory, en la Harvard Business School, que examinó la fisiología humana con un enfoque específico en el trabajo en la industria, el ejercicio y la nutrición.

En 1916, Karl Albert Hasselbalch (1874–1962), un médico y químico danés, compartió la autoría en un artículo con Christian Bohr en 1904 que describió el efecto Bohr, que mostró que la capacidad de la hemoglobina en la sangre para unirse al oxígeno era inversamente relacionada con la acidez de la sangre y la concentración del dióxido de carbono. La escala de pH fue introducida en 1909 por otro danés, Sørensen, y en 1912, Hasselbalch publicó mediciones del pH de la sangre. En 1916, Hasselbalch expresó la ecuación de Henderson en términos logarítmicos, de acuerdo con la escala logarítmica de pH, y así nació la ecuación de Henderson-Hasselbalch.

Medicina: el sistema tampón en la sangre

El pH normal de la sangre humana es de aproximadamente 7.4. El sistema tampón de carbonato en la sangre utiliza la siguiente reacción de equilibrio:

\[\ce{CO2}(g)+\ce{2H2O}(l)⇌\ce{H2CO3}(aq)⇌\ce{HCO3-}(aq)+\ce{H3O+}(aq)\]

La concentración de ácido carbónico, H₂CO₃ es aproximadamente 0.0012 M, y la concentración del ion carbonato de hidrógeno, \(\ce{HCO3-} \), es de alrededor de 0.024 M. Usando la ecuación de Henderson-Hasselbalch y el pKa de ácido carbónico en temperatura corporal, podemos calcular el pH de la sangre:

\[\mathrm{pH=p\mathit{K}_a+\log\dfrac{[base]}{[acid]}=6.1+\log\dfrac{0.024}{0.0012}=7.4}\]

El hecho de que la concentración de H₂CO₃ sea significativamente menor que la del ion \(\ce{HCO3-}\) puede parecer inusual, pero este desequilibrio se debe al hecho de que la mayoría de los subproductos de nuestro metabolismo que ingresan a nuestro torrente sanguíneo son ácidos. Por lo tanto, debe haber una mayor proporción de base que de ácido, de modo que no se exceda la capacidad del tampón.

El ácido láctico se produce en nuestros músculos cuando hacemos ejercicio. A medida que el ácido láctico ingresa al torrente sanguíneo, es neutralizado por el ion \(\ce{HCO3-}\), produciendo H₂CO₃. Luego, una enzima acelera la descomposición del exceso de ácido carbónico en dióxido de carbono y el agua, que puede eliminarse mediante la respiración. De hecho, además de los efectos reguladores del sistema de amortiguación de carbonatos en el pH de la sangre, el cuerpo usa la respiración para regular el pH de la sangre. Si el pH de la sangre disminuye demasiado, un aumento en la respiración elimina el CO₂ de la sangre a través de los pulmones, impulsando la reacción de equilibrio de tal manera que se reduce [H₃O⁺]. Si la sangre es demasiado alcalina, una frecuencia respiratoria más baja aumenta la concentración de CO₂ en la sangre, impulsando la reacción de equilibrio al revés, aumentando [H⁺] y restaurando un pH apropiado.

Resumen

Una solución que contiene una mezcla de un ácido y su base conjugada, o de una base y su ácido conjugado, se llama una solución tampón. A diferencia del caso de una solución de ácido, base o sal, la concentración de iones hidronio de una solución tampón no cambia mucho cuando se agrega una pequeña cantidad de ácido o base a la solución tampón. La base (o ácido) en el tampón reacciona con el ácido (o base) agregado.

Ecuaciones Clave

• pK_a = −log K_a
• pK_b = −log K_b
• \(\mathrm{pH=p\mathit{K}_a+\log\dfrac{[A^- ]}{[HA]}}\)

Glosario

capacidad del tampón

cantidad de un ácido o base que se puede agregar a un volumen de una solución tampón antes de que su pH cambie significativamente (generalmente en una unidad de pH)

tampón químico

mezcla de un ácido débil o una base débil y la sal de su conjugado; el pH de un tampón resiste el cambio cuando se agregan pequeñas cantidades de ácido o base

Ecuación de Henderson-Hasselbalch

ecuación utilizada para calcular el pH de las soluciones tampón

Contribuyentes

• Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.