35.1: Evaluación de Datos Analíticos
- Page ID
- 79075
El material de este apéndice está adaptado del libro de texto Quimiometrics Using R, el cual está disponible a través de LibreTexts utilizando este enlace. Además del material aquí, el libro de texto contiene instrucciones sobre cómo utilizar el lenguaje de programación estadística R para llevar a cabo los cálculos.
Tipos de datos
En el centro de cualquier análisis están los datos. A veces nuestros datos describen una categoría y a veces son numéricos; a veces nuestros datos transmiten orden y a veces no; a veces nuestros datos tienen una referencia absoluta y a veces tienen una referencia arbitraria; y a veces nuestros datos toman valores discretos y a veces toman valores continuos. Sea cual sea su forma, cuando recogemos datos nuestra intención es extraer de ellos información que pueda ayudarnos a resolver un problema.
Formas de describir datos
Si vamos a considerar cómo describir los datos, entonces necesitamos algunos datos con los que podamos trabajar. Idealmente, queremos datos que sean fáciles de recopilar y fáciles de entender. También es útil si puedes recopilar datos similares por tu cuenta para que puedas repetir lo que cubrimos aquí. Un sistema sencillo que cumple con estos criterios es analizar el contenido de bolsas de M&Ms. Aunque este sistema pueda parecer trivial, tenga en cuenta que reportar el porcentaje de M&Ms amarillos en una bolsa es análogo a reportar la concentración de Cu 2 + en una muestra de un mineral o agua: ambos expresan la cantidad de un analito presente en una unidad de su matriz.
Al inicio de este capítulo identificamos cuatro formas contrastantes de describir los datos: categórica vs numérica, ordenada vs. desordenada, referencia absoluta vs. referencia arbitraria y discreta vs continua. Para dar sentido a estos términos descriptivos, consideremos los datos en la Tabla\(\PageIndex{1}\), que incluye el año en que se compró y analizó la bolsa, el peso listado en el paquete, el tipo de M&Ms, el número de M&Ms amarillos en la bolsa, el porcentaje de las M&Ms que fueron rojas, el número total de M&Ms en la bolsa y sus filas correspondientes.
| ID de bolsa | año | peso (oz) | tipo | número amarillo | % rojo | M&Ms totales | rango (para total) |
|---|---|---|---|---|---|---|---|
| a | 2006 | 1.74 | maní | 2 | 27.8 | 18 | sexto |
| b | 2006 | 1.74 | maní | 3 | 4.35 | 23 | cuarto |
| c | 2000 | 0.80 | llano | 1 | 22.7 | 22 | quinto |
| d | 2000 | 0.80 | llano | 5 | 20.8 | 24 | tercero |
| e | 1994 | 10.0 | llano | 56 | 23.0 | 331 | segundo |
| f | 1994 | 10.0 | llano | 63 | 21.9 | 333 | primero |
Las entradas en Tabla\(\PageIndex{1}\) están organizadas por columna y por fila. La primera fila, a veces llamada fila de encabezado, identifica las variables que componen los datos. Cada fila adicional es el registro de una muestra y cada entrada en el registro de una muestra proporciona información sobre una de sus variables; así, los datos en la tabla enumeran el resultado para cada variable y para cada muestra.
Datos categóricos vs. numéricos
De las variables incluidas en la Tabla\(\PageIndex{1}\), algunas son categóricas y otras numéricas. Una variable categórica proporciona información cualitativa que podemos usar para describir las muestras relativas entre sí, o que podemos usar para organizar las muestras en grupos (o categorías). Para los datos en Tabla\(\PageIndex{1}\), id de bolsa, tipo y rango son variables categóricas.
Una variable numérica proporciona información cuantitativa que podemos usar en un cálculo significativo; por ejemplo, podemos usar el número de M&Ms amarillos y el número total de M&Ms para calcular una nueva variable que reporta el porcentaje de M&Ms que son amarillos. Para los datos en Tabla\(\PageIndex{1}\), año, peso (oz), número amarillo,% rojo M&Ms y M&Ms totales son variables numéricas.
También podemos usar una variable numérica para asignar muestras a grupos. Por ejemplo, podemos dividir las M&Ms simples en la Tabla\(\PageIndex{1}\) en dos grupos en función del peso de la muestra. Lo que hace que una variable numérica sea más interesante, sin embargo, es que podemos usarla para hacer comparaciones cuantitativas entre muestras; así, podemos informar que hay\(14.4 \times\) tantas M&Ms lisas en una bolsa de 10 oz. como en una bolsa de 0.8-oz.
\[\frac{333 + 331}{24 + 22} = \frac{664}{46} = 14.4 \nonumber \]
Aunque podríamos clasificar el año como una variable categórica, no una elección irrazonable, ya que podría servir como una forma útil de agrupar muestras, lo enumeramos aquí como una variable numérica porque puede servir como una variable predictiva útil en un análisis de regresión. Por otro lado, el rango no es una variable numérica, aunque reescribamos los rangos como números, ya que no hay cálculos significativos que podamos completar usando esta variable.
Datos nominales vs. ordinales
Las variables categóricas se describen como nominales u ordinales. Una variable categórica nominal no implica un orden particular; una variable categórica ordinal, por otro lado, coveys un sentido de orden significativo. Para las variables categóricas en Tabla\(\PageIndex{1}\), id de bolsa y tipo son variables nominales, y el rango es una variable ordinal.
Relación vs. datos de intervalo
Una variable numérica se describe como ratio o intervalo dependiendo de si tiene (ratio) o no tiene (intervalo) una referencia absoluta. Aunque podemos completar cálculos significativos usando cualquier variable numérica, el tipo de cálculo que podemos realizar depende de si los valores de la variable tienen o no una referencia absoluta.
Una variable numérica tiene una referencia absoluta si tiene un cero significativo, es decir, un cero que significa una cantidad medida de ninguno, contra el cual hacemos referencia a todas las demás mediciones de esa variable. Para las variables numéricas en Tabla\(\PageIndex{1}\), peso (oz), número amarillo,% rojo y M&Ms totales son variables de relación porque cada una tiene un cero significativo; año es una variable de intervalo porque su escala se refiere a un punto arbitrario en el tiempo, 1 BCE, y no al inicio del tiempo.
Para una variable ratio, podemos hacer comparaciones absolutas y relativas significativas entre dos resultados, pero solo comparaciones absolutas significativas para una variable de intervalo. Por ejemplo, considere la muestra e, que se colectó en 1994 y tiene 331 M&Ms, y la muestra d, que se colectó en 2000 y tiene 24 M&Ms. Podemos reportar una comparación absoluta significativa para ambas variables: la muestra e es seis años mayor que la muestra d y la muestra e tiene 307 M&Ms más que la muestra d. puede reportar una comparación relativa significativa para el número total de M&MS; hay
\[\frac{331}{24} = 13.8 \times \nonumber \]
tantas M&Ms en la muestra e como en la muestra d, pero no podemos reportar una comparación relativa significativa para el año porque una muestra recolectada en 2000 no es
\[\frac{2000}{1994} = 1.003 \times \nonumber \]
mayor que una muestra recolectada en 1994.
Datos discretos frente a datos continuos
Finalmente, la granularidad de una variable numérica proporciona una forma más de describir nuestros datos. Por ejemplo, podemos describir una variable numérica como discreta o continua. Una variable numérica es discreta si puede tomar solo valores específicos —típicamente, pero no siempre, un valor entero— entre sus límites; una variable continua puede tomar cualquier valor posible dentro de sus límites. Para los datos numéricos en la Tabla\(\PageIndex{1}\), año, número amarillo y M&M totales son discretos ya que cada uno está limitado a valores enteros. Las variables numéricas peso (oz) y% rojo, por otro lado, son variables continuas. Tenga en cuenta que el peso es una variable continua incluso si el dispositivo que usamos para medir el peso produce valores discretos.
Visualización de datos
El viejo dicho de que “una imagen vale más que 1000 palabras” puede no ser universalmente cierto, pero sí cierto cuando se trata del análisis de datos. Una buena visualización de datos, por ejemplo, nos permite ver patrones y relaciones que son menos evidentes cuando miramos datos dispuestos en una tabla, y proporciona una manera poderosa de contar la historia de nuestros datos. Supongamos que queremos estudiar la composición de paquetes de 1.69-oz (47.9-g) de M&Ms lisos. Obtenemos 30 bolsas de M&Ms (diez de cada una de las tres tiendas) y retiramos los M&Ms de cada bolsa uno por uno, registrando el número de M&Ms azules, marrones, verdes, naranjas, rojos y amarillos. También registramos el número de M&Ms amarillos M&Ms en los primeros cinco caramelos extraídos de cada bolsa, y registrar el peso neto real de los M&Ms en cada bolsa. \(\PageIndex{2}\)En la tabla se resumen los datos recopilados sobre estas muestras. La identificación de la bolsa identifica el orden en que se abrieron y analizaron las bolsas.
| bolsa | tienda | azul | marrón | verde | naranja | rojo | amarillo | Amarillo_First_Cinco | net_weight |
|---|---|---|---|---|---|---|---|---|---|
| 1 | CVS | 3 | 18 | 1 | 5 | 7 | 23 | 2 | 49.287 |
| 2 | CVS | 3 | 14 | 9 | 7 | 8 | 15 | 0 | 48.870 |
| 3 | Target | 4 | 14 | 5 | 10 | 10 | 16 | 1 | 51.250 |
| 4 | Kroger | 3 | 13 | 5 | 4 | 15 | 16 | 0 | 48.692 |
| 5 | Kroger | 3 | 16 | 5 | 7 | 8 | 18 | 1 | 48.777 |
| 6 | Kroger | 2 | 12 | 6 | 10 | 17 | 7 | 1 | 46.405 |
| 7 | CVS | 13 | 11 | 2 | 8 | 6 | 17 | 1 | 49.693 |
| 8 | CVS | 13 | 12 | 7 | 10 | 7 | 8 | 2 | 49.391 |
| 9 | Kroger | 6 | 17 | 5 | 4 | 8 | 16 | 1 | 48.196 |
| 10 | Kroger | 8 | 13 | 2 | 5 | 10 | 17 | 1 | 47.326 |
| 11 | Target | 9 | 20 | 1 | 4 | 12 | 13 | 3 | 50.974 |
| 12 | Target | 11 | 12 | 0 | 8 | 4 | 23 | 0 | 50.081 |
| 13 | CVS | 3 | 15 | 4 | 6 | 14 | 13 | 2 | 47.841 |
| 14 | Kroger | 4 | 17 | 5 | 6 | 14 | 10 | 2 | 48.377 |
| 15 | Kroger | 9 | 13 | 3 | 8 | 14 | 8 | 0 | 47.004 |
| 16 | CVS | 8 | 15 | 1 | 10 | 9 | 15 | 1 | 50.037 |
| 17 | CVS | 10 | 11 | 5 | 10 | 7 | 13 | 2 | 48.599 |
| 18 | Kroger | 1 | 17 | 6 | 7 | 11 | 14 | 1 | 48.625 |
| 19 | Target | 7 | 17 | 2 | 8 | 4 | 18 | 1 | 48.395 |
| 20 | Kroger | 9 | 13 | 1 | 8 | 7 | 22 | 1 | 51.730 |
| 21 | Target | 7 | 17 | 0 | 15 | 4 | 15 | 3 | 50.405 |
| 22 | CVS | 12 | 14 | 4 | 11 | 9 | 5 | 2 | 47.305 |
| 23 | Target | 9 | 19 | 0 | 5 | 12 | 12 | 0 | 49.477 |
| 24 | Target | 5 | 13 | 3 | 4 | 15 | 16 | 0 | 48.027 |
| 25 | CVS | 7 | 13 | 0 | 4 | 15 | 16 | 2 | 48.212 |
| 26 | Target | 6 | 15 | 1 | 13 | 10 | 14 | 1 | 51.682 |
| 27 | CVS | 5 | 17 | 6 | 4 | 8 | 19 | 1 | 50.802 |
| 28 | Kroger | 1 | 21 | 6 | 5 | 10 | 14 | 0 | 49.055 |
| 29 | Target | 4 | 12 | 6 | 5 | 13 | 14 | 2 | 46.577 |
| 30 | Target | 15 | 8 | 9 | 6 | 10 | 8 | 1 | 48.317 |
Habiendo recopilado nuestros datos, los examinamos a continuación en busca de posibles problemas, como valores faltantes (¿Olvidamos registrar el número de M&Ms marrones en alguna de nuestras muestras?) , por errores introducidos cuando registramos los datos (¿El punto decimal se registra incorrectamente para alguno de los pesos netos?) , o por resultados inusuales (¿Es realmente el caso de que esta bolsa solo tenga M&M amarilla?). También examinamos nuestros datos para identificar observaciones interesantes que tal vez deseemos explorar (Parece que la mayoría de los pesos netos son mayores que el peso neto enumerado en los paquetes individuales. ¿Por qué podría ser esto? ¿La diferencia es significativa?) Cuando nuestro conjunto de datos es pequeño generalmente podemos identificar posibles problemas y observaciones interesantes sin mucha dificultad; sin embargo, para un conjunto de datos grande, esto se convierte en un desafío. En lugar de tratar de examinar los valores individuales, podemos ver nuestros resultados visualmente. Si bien puede ser difícil encontrar un punto de datos único e impar cuando tenemos que revisar individualmente 1000 muestras, a menudo salta cuando miramos los datos usando uno o más de los enfoques que exploraremos en este capítulo.
Gráficas de puntos
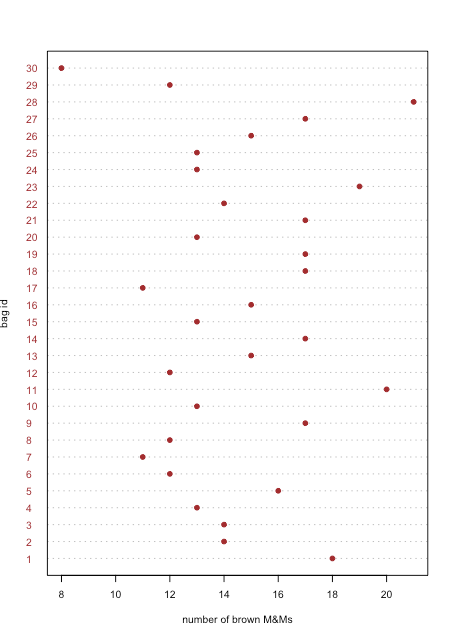
Una gráfica de puntos muestra datos para una variable, con el valor de cada muestra trazado en el eje x. Los puntos individuales se organizan a lo largo del eje y con la primera muestra en la parte inferior y la última muestra en la parte superior. La figura\(\PageIndex{1}\) muestra una gráfica de puntos para el número de M&Ms marrones en las 30 bolsas de M&Ms de Table\(\PageIndex{2}\). La distribución de los puntos aparece aleatoria ya que no existe correlación entre el id de muestra y el número de M&Ms marrones. Nos sorprendería que descubriéramos que los puntos estaban dispuestos de la parte inferior izquierda a la parte superior derecha ya que esto implica que el orden en que abrimos las bolsas determina si tienen muchos o unos pocos M&Ms marrones.
Gráficos de francos
Una gráfica de puntos proporciona una manera rápida de darnos la confianza de que nuestros datos están libres de patrones inusuales, pero a costa del espacio porque usamos el eje y para incluir el id de muestra como variable. Un gráfico de tiras usa el mismo eje x que una gráfica de puntos, pero no usa el eje y para distinguir entre muestras. Debido a que todas las muestras con el mismo número de M&Ms marrones aparecerán en el mismo lugar, haciendo imposible distinguirlas unas de otras, apilamos los puntos verticalmente para extenderlos, como se muestra en la Figura\(\PageIndex{2}\).
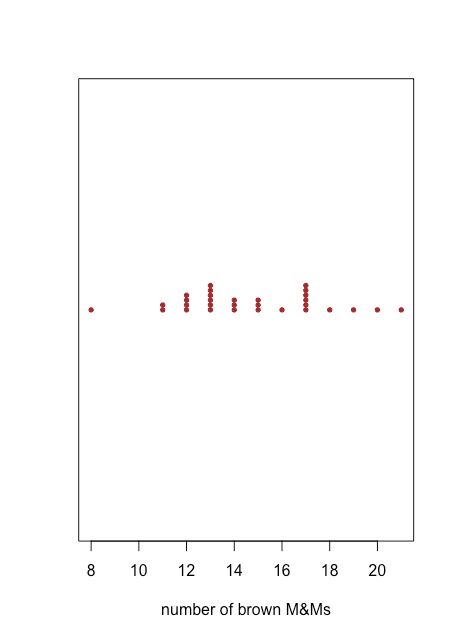
Tanto la gráfica de puntos en la Figura\(\PageIndex{1}\) como la gráfica de tira en la Figura\(\PageIndex{2}\) sugieren que hay una menor densidad de puntos en el límite inferior y el límite superior de nuestros resultados. Vemos, por ejemplo, que solo hay una bolsa cada una con 8, 16, 18, 19, 20 y 21 M&Ms marrones, pero hay seis bolsas cada una con 13 y 17 M&Ms marrones.
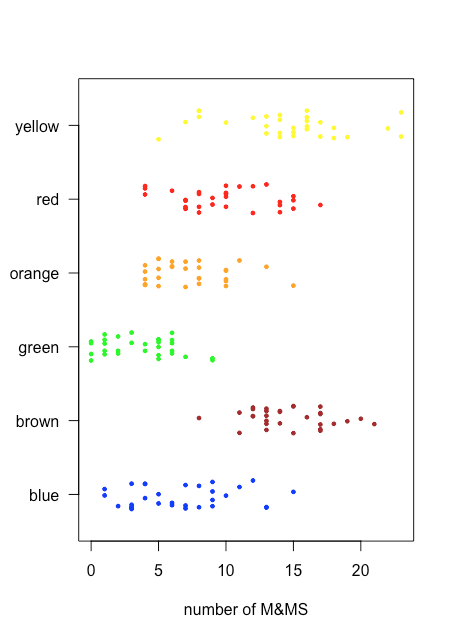
Debido a que un gráfico de franjas no utiliza el eje y para proporcionar información categórica significativa, podemos mostrar fácilmente varios diagramas de franjas a la vez. La figura\(\PageIndex{3}\) muestra esto para los datos de la Tabla\(\PageIndex{2}\). En lugar de apilar los puntos individuales, los fluctuamos aplicando un pequeño desplazamiento aleatorio a cada punto. Entre las cosas que aprendemos de este stripchart están que solo las M&Ms marrones y amarillas tienen recuentos superiores a 20 y que solo las M&Ms azules y verdes tienen recuentos de tres o menos M&Ms.
Parcelas de Caja y Bigotes
El diagrama de franjas en la Figura\(\PageIndex{3}\) es fácil de examinar porque el número de muestras, 30 bolsas y el número de M&Ms por bolsa es lo suficientemente pequeño como para que podamos ver los puntos individuales. A medida que aumenta la densidad de puntos, un diagrama de franjas se vuelve menos útil. Una gráfica de caja y bigotes proporciona una vista similar pero se enfoca en los datos en términos del rango de valores que abarcan el 50% medio de los datos.
La figura\(\PageIndex{4}\) muestra la gráfica de caja y bigotes para M&Ms marrones usando los datos de la Tabla\(\PageIndex{2}\). Las 30 muestras individuales se superponen como un diagrama de tira. La caja central divide el eje x en tres regiones: bolsas con menos de 13 M&Ms marrones (siete muestras), bolsas con entre 13 y 17 M&Ms marrones (19 muestras) y bolsas con más de 17 M&Ms marrones (cuatro muestras). Los límites de la caja están establecidos para que incluya al menos el 50% medio de nuestros datos. En este caso, la caja contiene 19 de las 30 muestras (63%) de las bolsas, ya que al mover cualquiera de los extremos de la caja hacia el centro se obtiene una caja que incluye menos del 50% de las muestras. La diferencia entre el límite superior de la caja (19) y su límite inferior (13) se denomina rango intercuartílico (IQR). La línea gruesa en el cuadro es la mediana, o valor medio (más sobre esto y el IQR en el siguiente capítulo). Las líneas discontinuas en cada extremo de la caja se llaman bigotes, y se extienden hasta el resultado más grande o menor que se encuentra dentro\(\pm 1.5 \times \text{IQR}\) del borde derecho o izquierdo de la caja, respectivamente.
Debido a que una gráfica de caja y bigotes no utiliza el eje y para proporcionar información categórica significativa, podemos mostrar fácilmente varias parcelas en el mismo marco. La figura\(\PageIndex{5}\) muestra esto para los datos de la Tabla\(\PageIndex{2}\). Tenga en cuenta que cuando un valor cae fuera de un bigote, como es el caso aquí para las M&Ms amarillas, se marca mostrándolo como un círculo abierto.
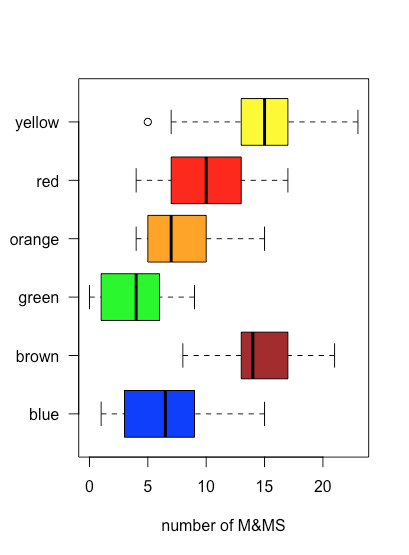
Un uso de una gráfica de caja y bigotes es examinar la distribución de las muestras individuales, particularmente con respecto a la simetría. A excepción de la muestra única que cae fuera de los bigotes, la distribución de M&Ms amarillos aparece simétrica: la mediana está cerca del centro de la caja y los bigotes se extienden por igual en ambas direcciones. La distribución de las M&Ms naranjas es asimétrica: la mitad de las muestras tienen 4—7 M&Ms (solo cuatro resultados posibles) y la mitad tienen 7—15 M&Ms (nueve posibles resultados), lo que sugiere que la distribución está sesgada hacia números más altos de M&Ms naranjas (ver Capítulo 5 para más información sobre las distribución de muestras).
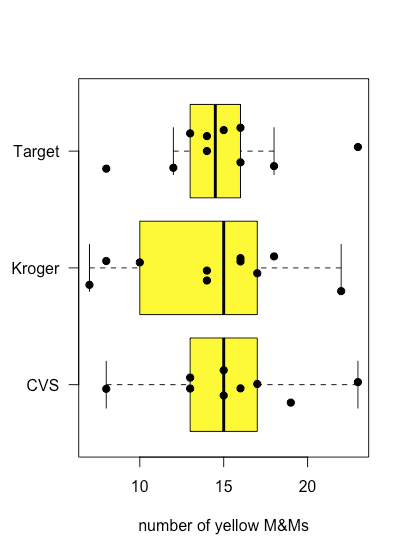
La figura\(\PageIndex{6}\) muestra parcelas de caja y bigotes para M&Ms amarillas agrupadas según la tienda donde se compraron las bolsas de M&Ms. Aunque las parcelas de caja y bigotes son bastante diferentes en términos de los tamaños relativos de las cajas y la longitud relativa de los bigotes, las gráficas de puntos sugieren que la distribución de los datos subyacentes es relativamente similar en que la mayoría de las bolsas contienen 12—18 M&M amarillos y solo unas pocas bolsas se desvían de estos límites. Estas observaciones son tranquilizadoras porque no esperamos que la elección de tienda afecte la composición de las bolsas de M&Ms. Si viéramos evidencia de que la elección de tienda afectó nuestros resultados, entonces miraríamos más de cerca las bolsas mismas para evidencia de una variable mal controlada, como el tipo (Did we comprar accidentalmente bolsas de mantequilla de maní M&Ms en una tienda?) o el número de lote del producto (¿Cambió el fabricante la composición de colores entre lotes?).
Parcelas de Barras
Aunque una gráfica de puntos, una gráfica de franjas y una gráfica de caja y bigotes proporcionan alguna evidencia cualitativa de cómo se distribuyen los valores de una variable, tendremos más que decir sobre la distribución de datos en el Capítulo 5, son menos útiles cuando necesitamos una imagen más cuantitativa de la distribución. Para ello podemos utilizar una gráfica de barras que muestre un recuento de cada resultado discreto. La figura\(\PageIndex{7}\) muestra gráficas de barras para M&Ms naranja y amarillo usando los datos de la Tabla\(\PageIndex{2}\).
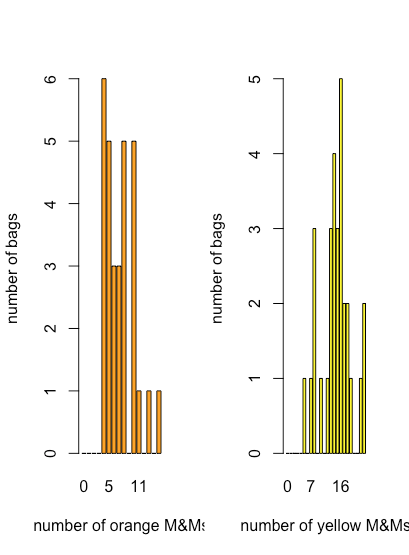
Aquí vemos que el número más común de M&Ms naranjas por bolsa es de cuatro, que también es el menor número de M&Ms naranjas por bolsa, y que hay una disminución general en el número de bolsas a medida que aumenta el número de M&M naranjas por bolsa. Para los M&Ms amarillos, el número más común de M&Ms por bolsa es de 16, que cae cerca de la mitad del rango de M&Ms amarillos.
Histogramas
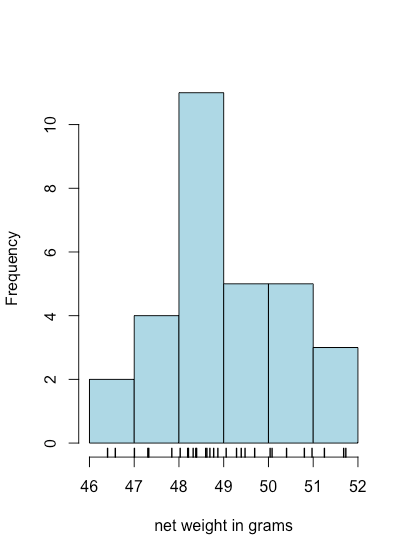
Una gráfica de barras es una forma útil de observar la distribución de resultados discretos, como los recuentos de M&Ms naranjas o amarillas, pero no es útil para datos continuos donde cada resultado es único. Un histograma, en el que mostramos el número de resultados que caen dentro de una secuencia de bins igualmente espaciados, proporciona una vista que es similar a la de una gráfica de barras pero que funciona con datos continuos. La figura\(\PageIndex{8}\), por ejemplo, muestra un histograma para los pesos netos de las 30 bolsas de M&Ms en la Tabla\(\PageIndex{2}\). Los valores individuales se muestran mediante las marcas hash verticales en la parte inferior del histograma.
Resumiendo datos
En la última sección se utilizaron datos recopilados de 30 bolsas de M&Ms para explorar diferentes formas de visualizar datos. En esta sección consideramos varias formas de resumir datos utilizando los pesos netos de las mismas bolsas de M&Ms. Aquí están los datos brutos.
| 49.287 | 48.870 | 51.250 | 48.692 | 48.777 | 46.405 |
| 49.693 | 49.391 | 48.196 | 47.326 | 50.974 | 50.081 |
| 47.841 | 48.377 | 47.004 | 50.037 | 48.599 | 48.625 |
| 48.395 | 51.730 | 50.405 | 47.305 | 49.477 | 48.027 |
| 48.212 | 51.682 | 50.802 | 49.055 | 46.577 | 48.317 |
Sin completar ningún cálculo, ¿qué conclusiones podemos sacar con solo mirar estos datos? Aquí hay algunos:
- Todos los pesos netos son mayores a 46 g y menores a 52 g.
- Como vemos en la Figura\(\PageIndex{9}\), una gráfica de caja y bigotes (superpuesta con un stripchart) y un histograma sugieren que la distribución de los pesos netos es razonablemente simétrica.
- La ausencia de puntos más allá de los bigotes de la trama de caja y bigotes sugiere que no hay pesos netos inusualmente grandes o insualmente pequeños.
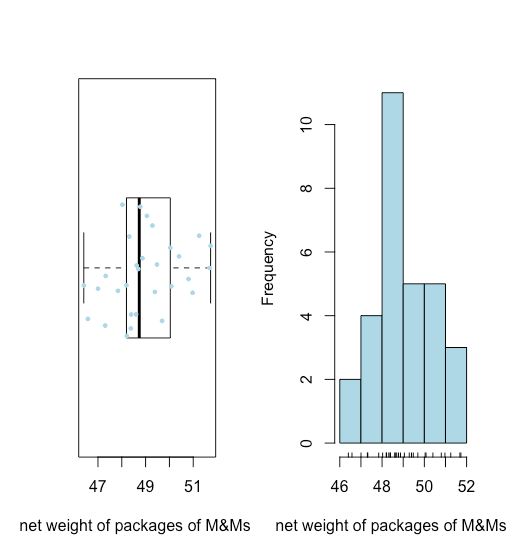
Ambas visualizaciones proporcionan una buena imagen cualitativa de los datos, sugiriendo que los resultados individuales están dispersos alrededor de algún valor central con más resultados más cercanos a ese valor central que a distancia de él. Ninguna visualización, sin embargo, describe los datos cuantitativamente. Lo que necesitamos es una manera conveniente de resumir los datos informando dónde están centrados los datos y qué tan variados son los resultados individuales alrededor de ese centro.
¿Dónde está el Centro?
Hay dos formas comunes de reportar el centro de un conjunto de datos: la media y la mediana.
La media,\(\overline{Y}\), es la media numérica obtenida sumando los resultados para todas las n observaciones y dividiendo por el número de observaciones
\[\overline{Y} = \frac{ \sum_{i = 1}^n Y_{i} } {n} = \frac{49.287 + 48.870 + \cdots + 48.317} {30} = 48.980 \text{ g} \nonumber \]
La mediana,\(\widetilde{Y}\), es el valor medio después de ordenar nuestras observaciones de menor a mayor, como mostramos aquí para nuestros datos.
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 | 47.841 |
| 48.027 | 48.196 | 48.212 | 48.317 | 48.377 | 48.395 |
| 48.599 | 48.625 | 48.692 | 48.777 | 48.870 | 49.055 |
| 49.287 | 49.391 | 49.477 | 49.693 | 50.037 | 50.081 |
| 50.405 | 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
Si tenemos un número impar de muestras, entonces la mediana es simplemente el valor medio, o
\[\widetilde{Y} = Y_{\frac{n + 1}{2}} \nonumber \]
donde n es el número de muestras. Si, como es el caso aquí, n es par, entonces
\[\widetilde{Y} = \frac {Y_{\frac{n}{2}} + Y_{\frac{n}{2}+1}} {2} = \frac {48.692 + 48.777}{2} = 48.734 \text{ g} \nonumber \]
Cuando nuestros datos tienen una distribución simétrica, como creemos que es el caso aquí, entonces la media y la mediana tendrán valores similares.
¿Cuál es la variación de los datos sobre el centro?
Hay cinco medidas comunes de la variación de datos sobre su centro: la varianza, la desviación estándar, el rango, el rango intercuartil y la diferencia media media.
La varianza, s 2, es una desviación cuadrada promedio de las observaciones individuales en relación con la media
\[s^{2} = \frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1} = \frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1} = 2.052 \nonumber \]
y la desviación estándar, s, es la raíz cuadrada de la varianza, lo que le da las mismas unidades que la media.
\[s = \sqrt{\frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1}} = \sqrt{\frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1}} = 1.432 \nonumber \]
El rango, w, es la diferencia entre el valor más grande y el más pequeño en nuestro conjunto de datos.
\[w = 51.730 \text{ g} - 46.405 \text{ g} = 5.325 \text{ g} \nonumber \]
El rango intercuartil, IQR, es la diferencia entre la mediana del 25% inferior de observaciones y la mediana del 25% superior de las observaciones; es decir, proporciona una medida del rango de valores que abarca el 50% medio de las observaciones. No existe una fórmula única y estándar para calcular el IQR, y diferentes algoritmos arrojan resultados ligeramente diferentes. Adoptaremos el algoritmo descrito aquí:
1. Divida el conjunto de datos ordenados por la mitad; si hay un número impar de valores, elimine la mediana del conjunto de datos completo. Para nuestros datos, la mitad inferior es
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 |
| 47.841 | 48.027 | 48.196 | 48.212 | 48.317 |
| 48.377 | 48.395 | 48.599 | 48.625 | 48.692 |
y la mitad superior es
| 48.777 | 48.870 | 49.055 | 49.287 | 49.391 |
| 49.477 | 49.693 | 50.037 | 50.081 | 50.405 |
| 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
2. Encuentra F L, la mediana para la mitad inferior de los datos, que para nuestros datos es de 48.196 g.
3. Encuentra F U, la mediana para la mitad superior de los datos, que para nuestros datos es 50.037 g.
4. El IQR es la diferencia entre F U y F L.
\[F_{U} - F_{L} = 50.037 \text{ g} - 48.196 \text{ g} = 1.841 \text{ g} \nonumber \]
La mediana de la desviación absoluta, MAD, es la mediana de las desviaciones absolutas de cada observación con respecto a la mediana de todas las observaciones. Para encontrar el MAD para nuestro conjunto de 30 pesos netos, primero restamos la mediana de cada muestra en la Tabla\(\PageIndex{3}\).
| 0.5525 | 0.1355 | 2.5155 | -0.0425 | 0.0425 | -2.3295 |
| 0.9585 | 0.6565 | -0.5385 | -1.4085 | 2.2395 | 1.3465 |
| -0.8935 | -0.3575 | -1.7305 | 1.3025 | -0.1355 | -0.1095 |
| -0.3395 | 2.9955 | 1.6705 | -1.4295 | 0.7425 | -0.7075 |
| -0.5225 | 2.9475 | 2.0675 | 0.3205 | -2.1575 | -0.4175 |
A continuación tomamos el valor absoluto de cada diferencia y las clasificamos de menor a mayor.
| 0.0425 | 0.0425 | 0.1095 | 0.1355 | 0.1355 | 0.3205 |
| 0.3395 | 0.3575 | 0.4175 | 0.5225 | 0.5385 | 0.5525 |
| 0.6565 | 0.7075 | 0.7425 | 0.8935 | 0.9585 | 1.3025 |
| 1.3465 | 1.4085 | 1.4295 | 1.6705 | 1.7305 | 2.0675 |
| 2.1575 | 2.2395 | 2.3295 | 2.5155 | 2.9475 | 2.9955 |
Finalmente, reportamos la mediana para estos valores ordenados como
\[\frac{0.7425 + 0.8935}{2} = 0.818 \nonumber \]
Medidas robustas frente a no robustas del centro y variación sobre el centro
Una buena pregunta para hacer es por qué podríamos desear más de una forma de reportar el centro de nuestros datos y la variación en nuestros datos sobre el centro. Supongamos que el resultado para la última de nuestras 30 muestras se reportó como 483.17 en lugar de 48.317. Que se trate de un desplazamiento accidental del punto decimal o de un resultado verdadero no nos es relevante aquí; lo que importa es su efecto sobre lo que informamos. Aquí un resumen del efecto de este valor en cada una de nuestras formas de resumir nuestros datos.
| estadística | datos originales | nuevos datos |
|---|---|---|
| media | 48.980 | 63.475 |
| mediana | 48.734 | 48.824 |
| varianza | 2.052 | 6285.938 |
| desviación estándar | 1.433 | 79.280 |
| gama | 5.325 | 436.765 |
| IQR | 1.841 | 1.885 |
| MAD | 0.818 | 0.926 |
Tenga en cuenta que la media, la varianza, la desviación estándar y el rango son muy sensibles al cambio en el último resultado, pero la mediana, el IQR y el MAD no lo son. La mediana, el IQR y el MAD se consideran estadísticas robustas porque son menos sensibles a un resultado inusual; los otros son, por supuesto, estadísticas no robustas. Ambos tipos de estadísticas tienen valor para nosotros, un punto al que volveremos de vez en cuando.
La distribución de datos
Cuando medimos algo, como el porcentaje de M&Ms amarillos en una bolsa de M&Ms, esperamos dos cosas:
- que hay un valor subyacente “verdadero” que nuestras mediciones deben aproximarse, y
- que los resultados de las mediciones individuales mostrarán alguna variación sobre ese valor “verdadero”
Las visualizaciones de datos, como gráficos de puntos, gráficos de franjas, gráficas de caja y bigotes, gráficas de barras, histogramas y diagramas de dispersión, a menudo sugieren que hay una estructura subyacente en nuestros datos. Por ejemplo, hemos visto que la distribución de M&Ms amarillos en bolsas de M&Ms es más o menos simétrica alrededor de su mediana, mientras que la distribución de M&Ms naranjas se inclinó hacia valores más altos. Esta estructura subyacente, o distribución, de nuestros datos, ya que afecta a cómo elegimos analizar nuestros datos. En este capítulo veremos más de cerca varias formas en las que se distribuyen los datos.
Terminología
Antes de considerar diferentes tipos de distribuciones, definamos algunos términos clave. Tal vez desee, también, revisar la discusión de diferentes tipos de datos en el Capítulo 2.
Poblaciones y Muestras
Una población incluye todas las mediciones posibles que podríamos hacer en un sistema, mientras que una muestra es el subconjunto de una población sobre la que realmente hacemos mediciones. Estas definiciones son fluidas. Una sola bolsa de M&Ms es una población si estamos interesados sólo en esa bolsa específica, pero no es más que una muestra de una caja que contiene un bruto (144) de bolsas individuales. Esa caja, en sí misma, puede ser una población, o puede ser una muestra de un lote de producción mucho mayor. Y así sucesivamente.
Distribuciones Discretas y Distribuciones Continua
En una distribución discreta los posibles resultados toman un conjunto limitado de valores específicos que son independientes de cómo hacemos nuestras mediciones. Cuando determinamos el número de M&Ms amarillos en una bolsa, los resultados se limitan a valores enteros. Podemos encontrar 13 M&Ms amarillos o 24 M&Ms amarillos, pero no podemos obtener un resultado de 15.43 M&Ms amarillos.
Para una distribución continua el resultado de una medición puede tomar cualquier valor posible entre un límite inferior y un límite superior, a pesar de que nuestro dispositivo de medición tiene una precisión limitada; así, cuando pesamos una bolsa de M&Ms en una balanza de tres dígitos y obtenemos un resultado de 49.287 g sabemos que su verdadera masa es mayores a 49.2865... g e inferiores a 49.2875... g.
Modelos teóricos para la distribución de datos
Hay cuatro tipos importantes de distribuciones que consideraremos en este capítulo: la distribución uniforme, la distribución binomial, la distribución de Poisson y la distribución normal o gaussiana. En las secciones anteriores se utilizó el análisis de bolsas de M&Ms para explorar formas de visualizar datos y resumir datos. Aquí utilizaremos el mismo conjunto de datos para explorar la distribución de los datos.
Distribución Uniforme
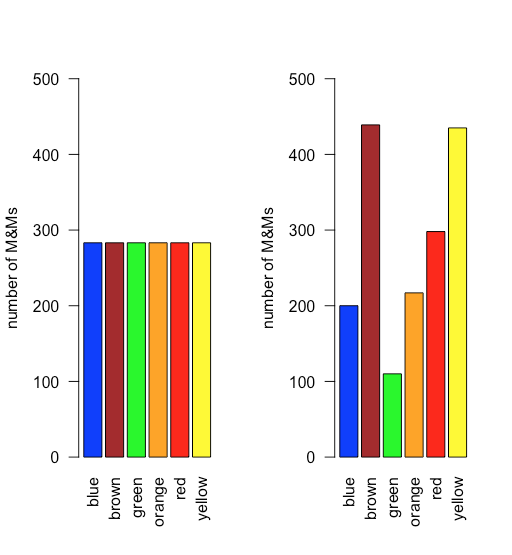
En una distribución uniforme, todos los resultados son igualmente probables. Supongamos que la población de M&Ms tiene una distribución uniforme. Si este es el caso, entonces, con seis colores, esperamos que cada color aparezca con una probabilidad de 1/6 o 16.7%. La figura\(\PageIndex{10}\) muestra una comparación de los resultados teóricos si dibujamos 1699 M&MS, el número total de M&Ms en nuestra muestra de 30 bolsas, de una población con una distribución uniforme (a la izquierda) a la distribución real de las 1699 M&M en nuestra muestra (a la derecha). ¡Parece poco probable que la población de M&Ms tenga una distribución uniforme de colores!
Distribución binomial
Una distribución binomial muestra la probabilidad de obtener un resultado particular en un número fijo de ensayos, donde se conocen las probabilidades de que ese resultado ocurra en un solo ensayo. Matemáticamente, una distribución binomial se define por la ecuación
\[P(X, N) = \frac {N!} {X! (N - X)!} \times p^{X} \times (1 - p)^{N - X} \nonumber \]
donde P (X, N) es la probabilidad de que el evento ocurra X veces en N ensayos, y donde p es la probabilidad de que el evento ocurra en un solo ensayo. La distribución binomial tiene una media teórica,\(\mu\), y una varianza teórica\(\sigma^2\), de
\[\mu = Np \quad \quad \quad \sigma^2 = Np(1 - p) \nonumber \]
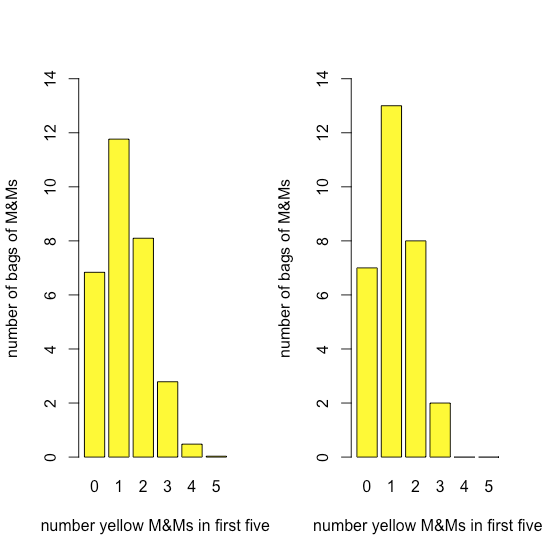
La figura\(\PageIndex{11}\) compara la distribución binomial esperada para el dibujo 0, 1, 2, 3, 4 o 5 M&M amarillos en los primeros cinco M&Ms —suponiendo que la probabilidad de dibujar un M&M amarillo es 435/1699, la relación entre el número de M&Ms amarillos y el número total de M&Ms— con la distribución real de resultados. La similitud entre los resultados teóricos y los reales parece evidente; en una sección posterior consideraremos formas de probar esta afirmación.
Distribución de Poisson
La distribución binomial es útil si queremos modelar la probabilidad de encontrar un número fijo de M&Ms amarillos en una muestra de M&Ms de tamaño fijo —como los primeros cinco M&Ms que extraemos de una bolsa— pero no la probabilidad de encontrar un número fijo de M&Ms amarillos en una sola bolsa porque hay cierta variabilidad en el número total de M&Ms por bolsa.
Una distribución de Poisson da la probabilidad de que un número dado de eventos ocurrirá en un intervalo fijo en tiempo o espacio si el evento tiene una tasa promedio conocida y si cada nuevo evento es independiente del evento anterior. Matemáticamente una distribución de Poisson se define por la ecuación
\[P(X, \lambda) = \frac {e^{-\lambda} \lambda^X} {X !} \nonumber \]
donde\(P(X, \lambda)\) es la probabilidad de que un evento ocurra X veces dada la tasa promedio del evento,\(\lambda\). La distribución de Poisson tiene una media teórica,\(\mu\), y una varianza teórica,\(\sigma^2\), que son cada una igual a\(\lambda\).
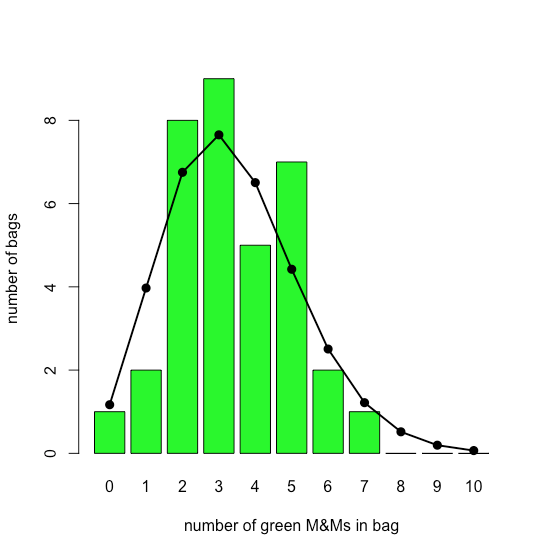
La gráfica de barras en la Figura\(\PageIndex{12}\) muestra la distribución real de M&Ms verdes en 35 bolsas pequeñas de M&Ms (según lo reportado por M. A. Xu-Friedman “Ilustrando conceptos de análisis cuántico con un modelo intuitivo de aula”, Adv. Physiol. Educ. 2013, 37, 112—116). Superpuesta a la parcela de barras se encuentra la distribución teórica de Poisson basada en su tasa promedio reportada de 3.4 M&Ms verdes por bolsa. La similitud entre los resultados teóricos y los reales parece evidente; en el Capítulo 6 consideraremos formas de probar esta afirmación.
Distribución Normal
Una distribución uniforme, una distribución binomial y una distribución de Poisson predicen la probabilidad de un evento discreto, como la probabilidad de encontrar exactamente dos M&Ms verdes en la siguiente bolsa de M&Ms que abrimos. No todos los datos que recopilamos son discretos. Los pesos netos de las bolsas de M&Ms son un ejemplo de datos continuos ya que la masa de una bolsa individual no se restringe a un conjunto discreto de valores permitidos. En muchos casos podemos modelar datos continuos usando una distribución normal (o gaussiana), lo que da la probabilidad de obtener un resultado particular, P (x), de una población con una media conocida,\(\mu\), y una varianza conocida,\(\sigma^2\). Matemáticamente una distribución normal se define por la ecuación
\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber \]
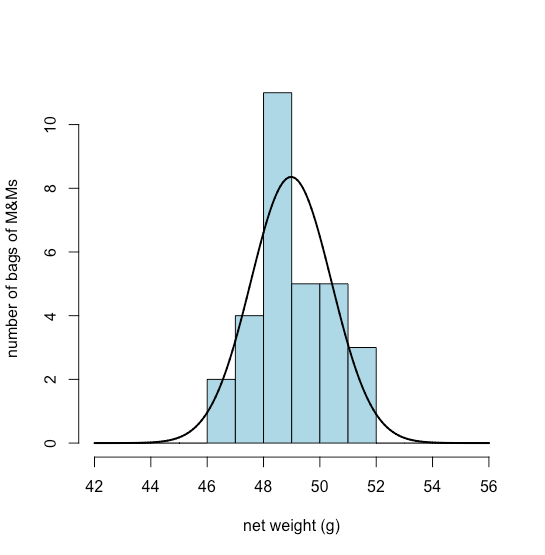
La figura\(\PageIndex{13}\) muestra la distribución normal esperada para los pesos netos de nuestra muestra de 30 bolsas de M&Ms si asumimos que su media\(\overline{X}\),, de 48.98 g y desviación estándar, s, de 1.433 g son buenos predictores de la media de la población,\(\mu\), y desviación estándar, \(\sigma\). Dada la pequeña muestra de 30 bolsas, el acuerdo entre el modelo y los datos parece razonable.
El teorema del límite central
Supongamos que tenemos una población para la cual una de sus propiedades tiene una distribución uniforme donde cada resultado entre 0 y 1 es igualmente probable. Si analizamos 10,000 muestras no debemos sorprendernos al encontrar que la distribución de estos 10000 resultados se ve uniforme, como lo muestra el histograma del lado izquierdo de la Figura\(\PageIndex{14}\). Si recolectamos 1000 muestras agrupadas, cada una de las cuales consta de 10 muestras individuales para un total de 10,000 muestras individuales, y reportamos los resultados promedio para estas 1000 muestras agrupadas, vemos algo interesante ya que su distribución, como lo muestra el histograma de la derecha, se ve notablemente como una normal distribución. Cuando extraemos muestras individuales de una distribución uniforme, cada resultado posible es igualmente probable, por lo que vemos la distribución a la izquierda. Cuando dibujamos una muestra agrupada que consta de 10 muestras individuales, sin embargo, es más probable que los valores promedio estén cerca de la mitad del rango de la distribución, como vemos a la derecha, porque la muestra agrupada probablemente incluye valores extraídos tanto de la mitad inferior como de la mitad superior de la distribución uniforme .
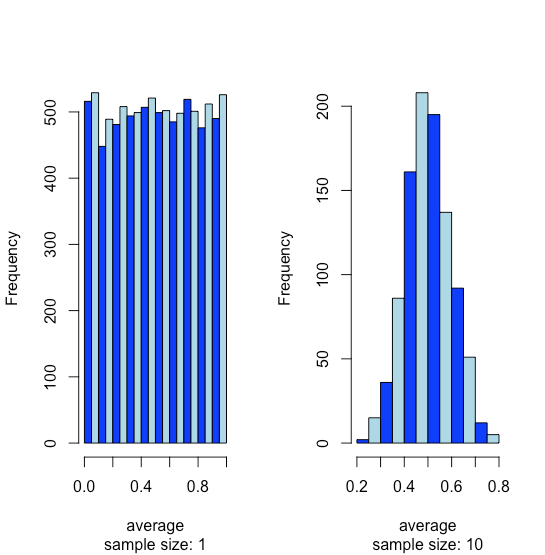
Esta tendencia a que surja una distribución normal cuando agrupamos muestras se conoce como el teorema del límite central. Como se muestra en la Figura\(\PageIndex{15}\), vemos un efecto similar con poblaciones que siguen una distribución binomial o una distribución de Poisson.
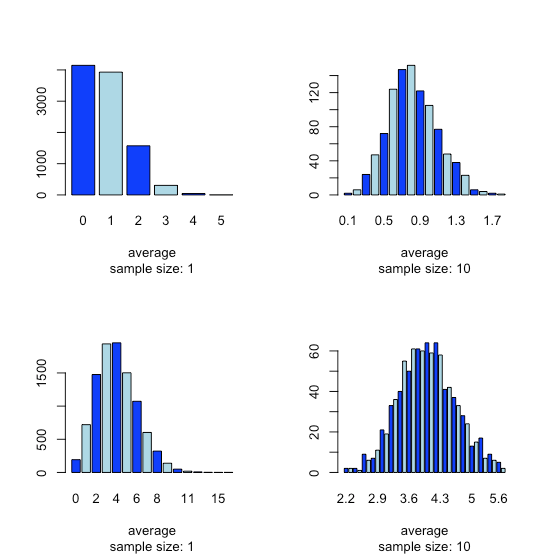
Podría preguntarse razonablemente si el teorema del límite central es importante ya que es poco probable que completemos 1000 análisis, cada uno de los cuales es el promedio de 10 ensayos individuales. Esto es engañoso. Cuando adquirimos una muestra de suelo, por ejemplo, consiste en muchas partículas individuales cada una de las cuales es una muestra individual del suelo. Nuestro análisis de esta muestra, por lo tanto, es la media para un gran número de partículas individuales de suelo. Debido a esto, el teorema del límite central es relevante.
Incertidumbre de datos
En la última sección examinamos cuatro formas en que las muestras individuales que recolectamos y analizamos se distribuyen alrededor de un valor central: una distribución uniforme, una distribución binomial, una distribución de Poisson y una distribución normal. También aprendimos que independientemente de cómo se distribuyan las muestras individuales, la distribución de promedios para múltiples muestras a menudo sigue una distribución normal. Esta tendencia a que surja una distribución normal cuando reportamos promedios para múltiples muestras se conoce como el teorema del límite central. En este capítulo analizamos más de cerca la distribución normal, examinando algunas de sus propiedades, y consideramos cómo podemos usar estas propiedades para decir algo más significativo sobre nuestros datos que simplemente reportar una media y una desviación estándar.
Propiedades de una Distribución Normal
Matemáticamente una distribución normal se define por la ecuación
\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber \]
donde\(P(x)\) es la probabilidad de obtener un resultado,\(x\), de una población con una media conocida,\(\mu\), y una desviación estándar conocida,\(\sigma\). La figura\(\PageIndex{16}\) muestra las curvas de distribución normal para\(\mu = 0\) con desviaciones estándar de 5, 10 y 20.
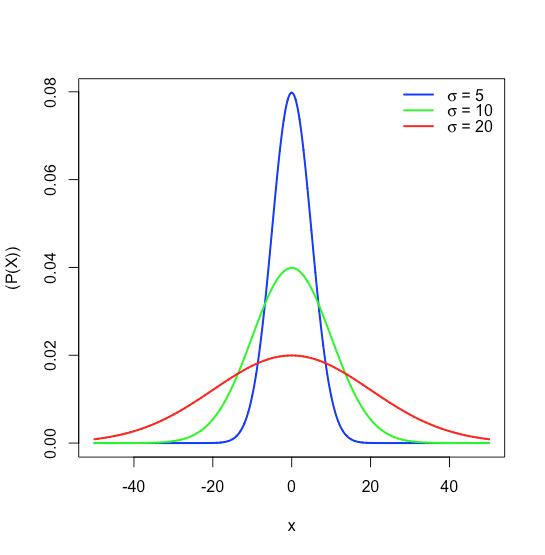
Debido a que la ecuación para una distribución normal depende únicamente de la media de la población\(\mu\), y de su desviación estándar\(\sigma\), la probabilidad de que una muestra extraída de una población tenga un valor entre dos límites arbitrarios cualesquiera es la misma para todas las poblaciones. Por ejemplo, la Figura\(\PageIndex{17}\) muestra que 68.26% de todas las muestras extraídas de una población normalmente distribuida tienen valores dentro del rango\(\mu \pm 1\sigma\), y sólo 0.14% tienen valores mayores que\(\mu + 3\sigma\).
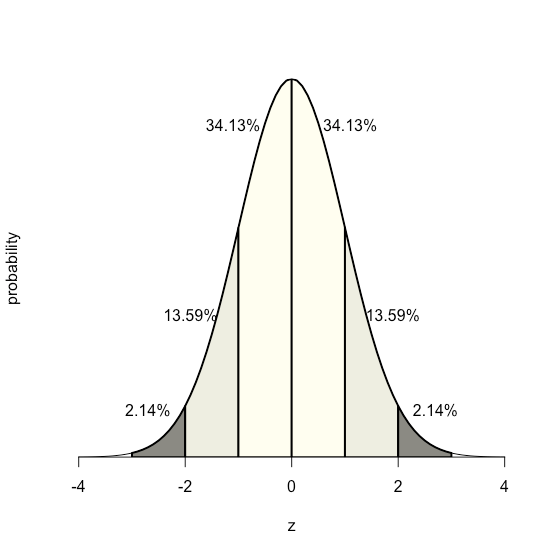
Esta característica de una distribución normal, que el área bajo la curva es la misma para todos los valores de, nos\(\sigma\) permite crear una tabla de probabilidad (ver Apéndice 2) basada en la desviación relativa,\(z\), entre un límite, x, y la media,\(\mu\).
\[z = \frac {x - \mu} {\sigma} \nonumber \]
El valor de\(z\) da el área bajo la curva entre ese límite y la cola más cercana de la distribución, como se muestra en la Figura\(\PageIndex{18}\).
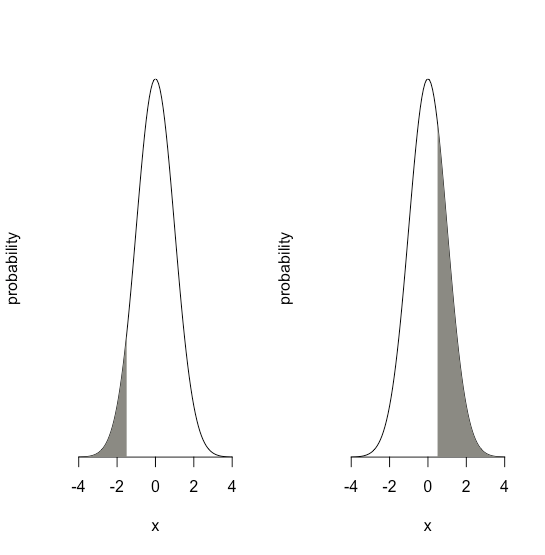
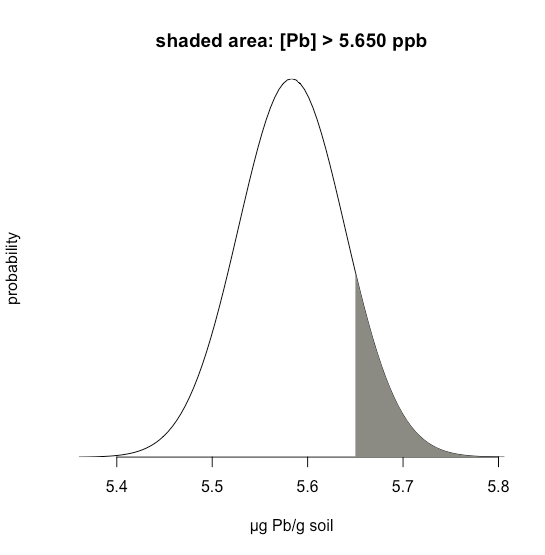
Supongamos que sabemos que\(\mu\) es 5.5833 ppb Pb y eso\(\sigma\) es 0.0558 ppb Pb para un material de referencia estándar particular (SRM). ¿Cuál es la probabilidad de que obtengamos un resultado mayor a 5.650 ppb si analizamos una sola muestra aleatoria extraída del SRM?
Solución
La figura\(\PageIndex{19}\) muestra la curva de distribución normal dada valores de 5.5833 ppb Pb para\(\mu\) y 0.0558 ppb Pb\(\sigma\). El área sombreada en las figuras es la probabilidad de obtener una muestra con una concentración de Pb mayor a 5.650 ppm. Para determinar la probabilidad, primero calculamos\(z\)
\[z = \frac {x - \mu} {\sigma} = \frac {5.650 - 5.5833} {0.0558} = 1.195 \nonumber \]
A continuación, buscamos la probabilidad en el Apéndice 2 para este valor de\(z\), que es el promedio de 0.1170 (para\(z = 1.19\)) y 0.1151 (para\(z = 1.20\)), o una probabilidad de 0.1160; así, esperamos que 11.60% de las muestras brinden un resultado mayor a 5.650 ppb Pb.
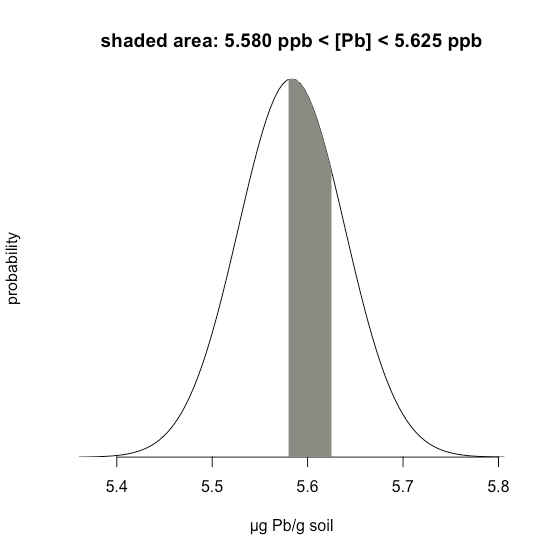
\(\PageIndex{1}\)El ejemplo considera un único límite: la probabilidad de que un resultado supere un solo valor. Pero, ¿y si queremos determinar la probabilidad de que una muestra tenga entre 5.580 g Pb y 5.625 g Pb?
Solución
En este caso nos interesa el área sombreada que se muestra en la Figura\(\PageIndex{20}\). Primero, calculamos\(z\) para el límite superior
\[z = \frac {5.625 - 5.5833} {0.0558} = 0.747 \nonumber \]
y luego calculamos\(z\) para el límite inferior
\[z = \frac {5.580 - 5.5833} {0.0558} = -0.059 \nonumber \]
Entonces, buscamos la probabilidad en el Apéndice 2 de que un resultado supere nuestro límite superior de 5.625, que es 0.2275, o 22.75%, y la probabilidad de que un resultado sea menor que nuestro límite inferior de 5.580, que es 0.4765, o 47.65%. El área total no sombreada es 71.4% del área total, por lo que el área sombreada corresponde a una probabilidad de
\[100.00 - 22.75 - 47.65 = 100.00 - 71.40 = 29.6 \% \nonumber \]
Intervalos de confianza
En la sección anterior, aprendimos a predecir la probabilidad de obtener un resultado particular si nuestros datos se distribuyen normalmente con un conocido\(\mu\) y uno conocido\(\sigma\). Por ejemplo, estimamos que 11.60% de las muestras extraídas al azar de un material de referencia estándar tendrán una concentración de Pb mayor a 5.650 ppb dada a\(\mu\) de 5.5833 ppb y a\(\sigma\) de 0.0558 ppb. En esencia, se determinó de cuántas desviaciones estándar es 5.650\(\mu\) y se utilizó esta para definir la probabilidad dada el área estándar bajo una curva de distribución normal.
Podemos verlo de otra manera haciendo la siguiente pregunta: Si recolectamos una sola muestra al azar de una población con un conocido\(\mu\) y otro conocido\(\sigma\), ¿dentro de qué rango de valores podríamos esperar razonablemente encontrar el resultado de la muestra 95% del tiempo? Reorganización de la ecuación
\[z = \frac {x - \mu} {\sigma} \nonumber \]
y resolviendo para\(x\) da
\[x = \mu \pm z \sigma = 5.5833 \pm (1.96)(0.0558) = 5.5833 \pm 0.1094 \nonumber \]
donde a\(z\) de 1.96 corresponde al 95% del área bajo la curva; llamamos a esto un intervalo de confianza del 95% para una sola muestra.
Por lo general, es una mala idea sacar una conclusión del resultado de un solo experimento; en cambio, solemos recolectar varias muestras y hacer la pregunta de esta manera: Si recolectamos muestras\(n\) aleatorias de una población con un conocido\(\mu\) y otro conocido\(\sigma\), dentro de qué rango de valores podríamos razonablemente esperar encontrar la media de estas muestras el 95% de las veces?
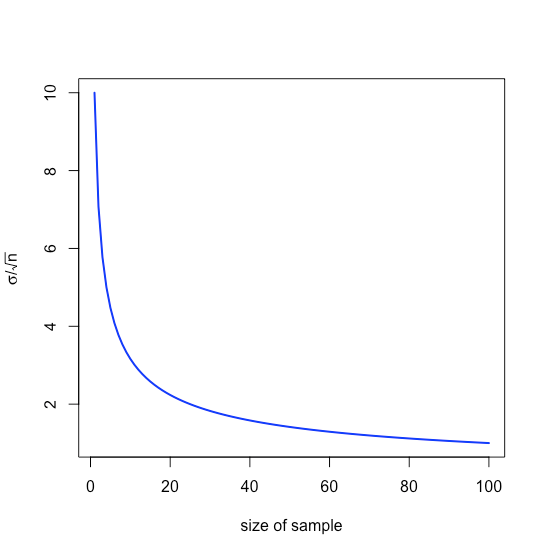
Podemos esperar razonablemente que la desviación estándar para la media de varias muestras sea menor que la desviación estándar para un conjunto de muestras individuales; de hecho lo es y se da como
\[\sigma_{\bar{x}} = \frac {\sigma} {\sqrt{n}} \nonumber \]
donde\(\frac {\sigma} {\sqrt{n}}\) se llama el error estándar de la media. Por ejemplo, si recolectamos tres muestras del material de referencia estándar descrito anteriormente, entonces esperamos que la media para estas tres muestras se encuentre dentro de un rango
\[\bar{x} = \mu \pm z \sigma_{\bar{X}} = \mu \pm \frac {z \sigma} {\sqrt{n}} = 5.5833 \pm \frac{(1.96)(0.0558)} {\sqrt{3}} = 5.5833 \pm 0.0631 \nonumber \]
es decir,\(\pm 0.0631\) ppb alrededor\(\mu\), un rango que es menor que el de\(\pm 0.1094\) ppb cuando analizamos muestras individuales. Obsérvese que el valor relativo para nosotros de aumentar el tamaño de la muestra disminuye a\(n\) medida que aumenta debido al término raíz cuadrada, como se muestra en la Figura\(\PageIndex{21}\).
Nuestro tratamiento hasta el momento supone que conocemos\(\mu\) y\(\sigma\) para la población parental, pero rara vez conocemos estos valores; en cambio, examinamos muestras extraídas de la población parental y hacemos la siguiente pregunta: Dada la media de la muestra\(\bar{x}\),, y su desviación estándar,\(s\), cuál es nuestra mejor estimación de la media de la población\(\mu\), y su desviación estándar,\(\sigma\).
Para hacer esta estimación, reemplazamos la desviación estándar de la población,\(\sigma\), por la desviación estándar,\(s\), para nuestras muestras, reemplazamos la media de la población,\(\mu\), por la media,\(\bar{x}\), para nuestras muestras,\(z\) reemplazamos por\(t\), donde el valor de\(t\) depende de el número de muestras,\(n\)
\[\bar{x} = \mu \pm \frac{ts}{\sqrt{n}} \nonumber \]
y luego reorganizar la ecuación para resolver\(\mu\).
\[\mu = \bar{x} \pm \frac {ts} {\sqrt{n}} \nonumber \]
A esto lo llamamos un intervalo de confianza. Los valores para\(t\) están disponibles en tablas (ver Apéndice 3) y dependen del nivel de probabilidad,\(\alpha\), donde\((1 − \alpha) \times 100\) está el nivel de confianza, y los grados de libertad,\(n − 1\); tenga en cuenta que para cualquier nivel de probabilidad,\(t \longrightarrow z\) como\(n \longrightarrow \infty\).
Debemos prestar especial atención a lo que significa este intervalo de confianza y a lo que no significa:
- No significa que exista una probabilidad del 95% de que la media de la población esté en el rango\(\mu = \bar{x} \pm ts\) porque nuestras mediciones pueden estar sesgadas o la distribución normal puede ser inapropiada para nuestro sistema.
- Proporciona nuestra mejor estimación de la media de la población,\(\mu\) dado nuestro análisis de\(n\) muestras extraídas al azar de la población parental; una muestra diferente, sin embargo, dará un intervalo de confianza diferente y, por lo tanto, una estimación diferente para\(\mu\).
Prueba de la significancia de los datos
Un intervalo de confianza es una manera útil de reportar el resultado de un análisis porque establece límites sobre el resultado esperado. En ausencia de error determinado, o sesgo, un intervalo de confianza basado en la media de una muestra indica el rango de valores en el que esperamos encontrar la media de la población. Cuando reportamos un intervalo de confianza del 95% para la masa de un centavo como 3.117 g ± 0.047 g, por ejemplo, estamos afirmando que solo hay un 5% de probabilidad de que la masa esperada del centavo sea inferior a 3.070 g o superior a 3.164 g.
Debido a que un intervalo de confianza es una declaración de probabilidad, nos permite considerar preguntas comparativas, como estas:
“¿Los resultados de un método recién desarrollado para determinar el colesterol en sangre son significativamente diferentes de los obtenidos mediante un método estándar?”
“¿Existe una variación significativa en la composición del agua de lluvia recolectada en diferentes sitios a favor del viento de una planta de servicios públicos que quema carbón?”
En este capítulo introducimos un enfoque general que utiliza datos experimentales para hacer y responder a tales preguntas, un enfoque que llamamos pruebas de significación.
La confiabilidad de las pruebas de significancia recientemente ha recibido mucha atención —véase Nuzzo, R. “Método científico: errores estadísticos”, Nature, 2014, 506, 150—152 para una discusión general de los temas— por lo que es apropiado comenzar este capítulo por señalando la necesidad de garantizar que nuestros datos y nuestra pregunta de investigación sean compatibles para que no leamos más en un análisis estadístico de lo que nuestros datos permiten; ver Leek, J. T.; Peng, R. D. “¿Cuál es la Pregunta? Science, 2015, 347, 1314-1315 para una útil discusión de seis preguntas comunes de investigación.
En el contexto de la química analítica, las pruebas de significancia suelen ir acompañadas de un análisis exploratorio de datos
“¿Hay alguna razón para sospechar que existe una diferencia entre estos dos métodos analíticos cuando se aplican a una muestra común?”
o un análisis de datos inferenciales.
“¿Hay alguna razón para sospechar que existe una relación entre estas dos mediciones independientes?”
Un resultado estadísticamente significativo para este tipo de preguntas de investigación analítica generalmente conduce al diseño de experimentos adicionales que son más adecuados para hacer predicciones o explicar una relación causal subyacente. Una prueba de significancia es el primer paso para construir una mayor comprensión de un problema analítico, ¡no la respuesta final a ese problema!
Pruebas de significancia
Consideremos el siguiente problema. Para determinar si un medicamento es efectivo para disminuir las concentraciones de glucosa en sangre, recolectamos dos conjuntos de muestras de sangre de un paciente. Recolectamos un conjunto de muestras inmediatamente antes de administrar el medicamento, y recolectamos el segundo conjunto de muestras varias horas después. Después de analizar las muestras, reportamos sus respectivas medias y varianzas. ¿Cómo decidimos si el medicamento logró disminuir la concentración de glucosa en sangre del paciente?
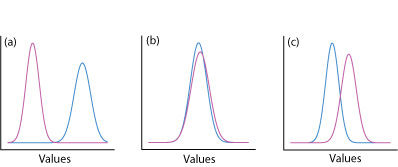
Una forma de responder a esta pregunta es construir una curva de distribución normal para cada muestra y comparar las dos curvas entre sí. En la Figura se muestran tres posibles resultados\(\PageIndex{22}\). En la Figura\(\PageIndex{22a}\), hay una separación completa de las dos curvas de distribución normal, lo que sugiere que las dos muestras son significativamente diferentes entre sí. En la Figura\(\PageIndex{22b}\), las curvas de distribución normal para las dos muestras se superponen casi completamente entre sí, lo que sugiere que la diferencia entre las muestras es insignificante. La figura\(\PageIndex{22c}\), sin embargo, nos presenta un dilema. Aunque las medias para las dos muestras parecen diferentes, el solapamiento de sus curvas de distribución normal sugiere que un número significativo de posibles resultados podrían pertenecer a cualquiera de las dos distribuciones. En este caso lo mejor que podemos hacer es hacer una declaración sobre la probabilidad de que las muestras sean significativamente diferentes entre sí.
El proceso mediante el cual determinamos la probabilidad de que haya una diferencia significativa entre dos muestras se denomina prueba de significancia o prueba de hipótesis. Antes de discutir ejemplos específicos, primero establezcamos un enfoque general para la realización e interpretación de una prueba de significación.
Construyendo una prueba de significancia
El propósito de una prueba de significancia es determinar si la diferencia entre dos o más resultados es lo suficientemente grande como para que nos sintamos cómodos afirmando que la diferencia no puede explicarse por errores indeterminados. El primer paso para construir una prueba de significancia es plantear el problema como una pregunta de sí o no, como
“¿Este medicamento es efectivo para bajar los niveles de glucosa en sangre de un paciente?”
Una hipótesis nula y una hipótesis alternativa definen las dos posibles respuestas a nuestra pregunta de sí o no. La hipótesis nula, H 0, es que los errores indeterminados son suficientes para explicar cualquier diferencia entre nuestros resultados. La hipótesis alternativa, H A, es que las diferencias en nuestros resultados son demasiado grandes para ser explicadas por error aleatorio y que deben ser determinadas en la naturaleza. Probamos la hipótesis nula, que o bien retenemos o rechazamos. Si rechazamos la hipótesis nula, entonces debemos aceptar la hipótesis alternativa y concluir que la diferencia es significativa.
No rechazar una hipótesis nula no es lo mismo que aceptarla. Conservamos una hipótesis nula porque no tenemos pruebas suficientes para demostrarla incorrecta. Es imposible probar que una hipótesis nula es cierta. Este es un punto importante y fácil de olvidar. Para apreciar este punto usemos estos datos para la masa de 100 centavos circulantes de Estados Unidos.
| Penny | Peso (g) | Penny | Peso (g) | Penny | Peso (g) | Penny | Peso (g) |
|---|---|---|---|---|---|---|---|
| 1 | 3.126 | 26 | 3.073 | 51 | 3.101 | 76 | 3.086 |
| 2 | 3.140 | 27 | 3.084 | 52 | 3.049 | 77 | 3.123 |
| 3 | 3.092 | 28 | 3.148 | 53 | 3.082 | 78 | 3.115 |
| 4 | 3.095 | 29 | 3.047 | 54 | 3.142 | 79 | 3.055 |
| 5 | 3.080 | 30 | 3.121 | 55 | 3.082 | 80 | 3.057 |
| 6 | 3.065 | 31 | 3.116 | 56 | 3.066 | 81 | 3.097 |
| 7 | 3.117 | 32 | 3.005 | 57 | 3.128 | 82 | 3.066 |
| 8 | 3.034 | 33 | 3.115 | 58 | 3.112 | 83 | 3.113 |
| 9 | 3.126 | 34 | 3.103 | 59 | 3.085 | 84 | 3.102 |
| 10 | 3.057 | 35 | 3.086 | 60 | 3.086 | 85 | 3.033 |
| 11 | 3.053 | 36 | 3.103 | 61 | 3.084 | 86 | 3.112 |
| 12 | 3.099 | 37 | 3.049 | 62 | 3.104 | 87 | 3.103 |
| 13 | 3.065 | 38 | 2.998 | 63 | 3.107 | 88 | 3.198 |
| 14 | 3.059 | 39 | 3.063 | 64 | 3.093 | 89 | 3.103 |
| 15 | 3.068 | 40 | 3.055 | 65 | 3.126 | 90 | 3.126 |
| 16 | 3.060 | 41 | 3.181 | 66 | 3.138 | 91 | 3.111 |
| 17 | 3.078 | 42 | 3.108 | 67 | 3.131 | 92 | 3.126 |
| 18 | 3.125 | 43 | 3.114 | 68 | 3.120 | 93 | 3.052 |
| 19 | 3.090 | 44 | 3.121 | 69 | 3.100 | 94 | 3.113 |
| 20 | 3.100 | 45 | 3.105 | 70 | 3.099 | 95 | 3.085 |
| 21 | 3.055 | 46 | 3.078 | 71 | 3.097 | 96 | 3.117 |
| 22 | 3.105 | 47 | 3.147 | 72 | 3.091 | 97 | 3.142 |
| 23 | 3.063 | 48 | 3.104 | 73 | 3.077 | 98 | 3.031 |
| 24 | 3.083 | 49 | 3.146 | 74 | 3.178 | 99 | 3.083 |
| 25 | 3.065 | 50 | 3.095 | 75 | 3.054 | 100 | 3.104 |
Después de mirar los datos podríamos proponer las siguientes hipótesis nulas y alternativas.
H 0: La masa de un centavo estadounidense circulante está entre 2.900 g y 3.200 g
H A: La masa de un centavo circulante estadounidense puede ser inferior a 2.900 g o superior a 3.200 g
Para probar la hipótesis nula encontramos un centavo y determinamos su masa. Si la masa del centavo es de 2.512 g entonces podemos rechazar la hipótesis nula y aceptar la hipótesis alternativa. Supongamos que la masa del centavo es de 3.162 g. Aunque este resultado aumenta nuestra confianza en la hipótesis nula, no prueba que la hipótesis nula sea correcta porque el siguiente centavo que muestremos podría pesar menos de 2.900 g o más de 3.200 g.
Después de exponer las hipótesis nulas y alternativas, el segundo paso es elegir un nivel de confianza para el análisis. El nivel de confianza define la probabilidad de que rechacemos incorrectamente la hipótesis nula cuando es, de hecho, cierta. Podemos expresar esto como nuestra confianza en que tenemos razón al rechazar la hipótesis nula (e.g. 95%), o como la probabilidad de que seamos incorrectos al rechazar la hipótesis nula. Para este último, el nivel de confianza se da como\(\alpha\), donde
\[\alpha = 1 - \frac {\text{confidence interval (%)}} {100} \nonumber \]
Para un nivel de confianza del 95%,\(\alpha\) es de 0.05.
El tercer paso consiste en calcular un estadístico de prueba apropiado y compararlo con un valor crítico. El valor crítico del estadístico de prueba define un punto de interrupción entre valores que nos llevan a rechazar o retener la hipótesis nula, que es el cuarto y último paso de una prueba de significancia. Como veremos en las secciones que siguen, la forma en que calculemos el estadístico de prueba depende de lo que estemos comparando.
Los cuatro pasos para un análisis estadístico de los datos mediante una prueba de significancia:
- Plantar una pregunta, y exponer la hipótesis nula, H 0, y la hipótesis alternativa, H A.
- Elija un nivel de confianza para el análisis estadístico.
- Calcular un estadístico de prueba apropiado y compararlo con un valor crítico.
- O bien conservar la hipótesis nula, o rechazarla y aceptar la hipótesis alternativa.
Pruebas de significancia de una cola y dos colas
Supongamos que queremos evaluar la precisión de un nuevo método analítico. Podríamos usar el método para analizar un Material de Referencia Estándar que contenga una concentración conocida de analito,\(\mu\). Analizamos el estándar varias veces, obteniendo un valor medio\(\overline{X}\), para la concentración del analito. Nuestra hipótesis nula es que no hay diferencia entre\(\overline{X}\) y\(\mu\)
\[H_0 \text{: } \overline{X} = \mu \nonumber \]
Si realizamos la prueba de significancia en\(\alpha = 0.05\), entonces conservamos la hipótesis nula si un intervalo de confianza del 95% alrededor\(\overline{X}\) contiene\(\mu\). Si la hipótesis alternativa es
\[H_\text{A} \text{: } \overline{X} \neq \mu \nonumber \]
entonces rechazamos la hipótesis nula y aceptamos la hipótesis alternativa si\(\mu\) se encuentra en las áreas sombreadas en cualquiera de los extremos de la curva de distribución de probabilidad de la muestra (Figura\(\PageIndex{23a}\)). Cada una de las áreas sombreadas representa 2.5% del área bajo la curva de distribución de probabilidad, para un total de 5%. Esta es una prueba de significancia de dos colas porque rechazamos la hipótesis nula para valores de ambos\(\mu\) extremos de la curva de distribución de probabilidad de la muestra.
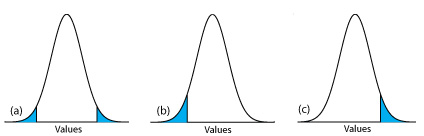
Podemos escribir la hipótesis alternativa de dos maneras adicionales
\[H_\text{A} \text{: } \overline{X} > \mu \nonumber \]
\[H_\text{A} \text{: } \overline{X} < \mu \nonumber \]
rechazando la hipótesis nula si\(\mu\) cae dentro de las áreas sombreadas que se muestran en la Figura\(\PageIndex{23b}\) o Figura\(\PageIndex{23c}\), respectivamente. En cada caso el área sombreada representa el 5% del área bajo la curva de distribución de probabilidad. Estos son ejemplos de una prueba de significancia de una cola.
Para un nivel de confianza fijo, una prueba de significancia de dos colas es la prueba más conservadora porque rechazar la hipótesis nula requiere una mayor diferencia entre los resultados que estamos comparando. En la mayoría de las situaciones no tenemos ninguna razón particular para esperar que un resultado debe ser mayor (o debe ser menor) que el otro resultado. Este es el caso, por ejemplo, cuando evaluamos la precisión de un nuevo método analítico. Una prueba de significancia de dos colas, por lo tanto, suele ser la elección adecuada.
Reservamos una prueba de significancia de una cola para una situación en la que específicamente estamos interesados en saber si un resultado es mayor (o menor) que el otro resultado. Por ejemplo, una prueba de significancia de una cola es apropiada si estamos evaluando la capacidad de un medicamento para disminuir los niveles de glucosa en sangre. En este caso solo nos interesa si los niveles de glucosa después de administrar el medicamento son menores que los niveles de glucosa antes de iniciar el tratamiento. Si el nivel de glucosa en sangre de un paciente es mayor después de administrar el medicamento, entonces conocemos la respuesta —la medicación no funcionó— y no necesitamos realizar un análisis estadístico.
Errores en las pruebas de significancia
Debido a que una prueba de significancia se basa en la probabilidad, su interpretación está sujeta a error. En una prueba de significancia,\(\alpha\) define la probabilidad de rechazar una hipótesis nula que es verdadera. Cuando realizamos una prueba de significancia en\(\alpha = 0.05\), hay un 5% de probabilidad de que rechacemos incorrectamente la hipótesis nula. Esto se conoce como error tipo 1, y su riesgo siempre es equivalente a\(\alpha\). Un error tipo 1 en una prueba de significancia de dos colas o una cola corresponde a las áreas sombreadas bajo las curvas de distribución de probabilidad en la Figura\(\PageIndex{23}\).
Un segundo tipo de error ocurre cuando conservamos una hipótesis nula aunque sea falsa. Este es un error tipo 2, y la probabilidad de que ocurra es\(\beta\). Desafortunadamente, en la mayoría de los casos no podemos calcular ni estimar el valor para\(\beta\). La probabilidad de un error tipo 2, sin embargo, es inversamente proporcional a la probabilidad de un error tipo 1.
Minimizar un error de tipo 1 al disminuir\(\alpha\) aumenta la probabilidad de un error de tipo 2. Cuando elegimos un valor para\(\alpha\) debemos comprometernos entre estos dos tipos de error. La mayoría de los ejemplos de este texto utilizan un nivel de confianza del 95% (\(\alpha = 0.05\)) porque esto suele ser un compromiso razonable entre los errores tipo 1 y tipo 2 para el trabajo analítico. No es inusual, sin embargo, utilizar un nivel de confianza más estricto (por ejemplo\(\alpha = 0.01\)) o más indulgente (por ejemplo\(\alpha = 0.10\)) cuando la situación lo requiere.
Pruebas de significancia para distribuciones normales
Una distribución normal es la distribución más común para los datos que recopilamos. Debido a que el área entre dos límites cualesquiera de una curva de distribución normal está bien definida, es sencillo construir y evaluar pruebas de significancia.
Comparando\(\overline{X}\) con\(\mu\)
Una forma de validar un nuevo método analítico es analizar una muestra que contiene una cantidad conocida de analito,\(\mu\). Para juzgar la precisión del método analizamos varias porciones de la muestra, determinamos la cantidad promedio de analito en la muestra y usamos una prueba de significancia\(\overline{X}\) para compararla\(\mu\).\(\overline{X}\) La hipótesis nula es que la diferencia entre\(\overline{X}\) y\(\mu\) se explica por errores indeterminados que afectan nuestra determinación de\(\overline{X}\). La hipótesis alternativa es que la diferencia entre\(\overline{X}\) y\(\mu\) es demasiado grande para ser explicada por error indeterminado.
\[H_0 \text{: } \overline{X} = \mu \nonumber \]
\[H_A \text{: } \overline{X} \neq \mu \nonumber \]
El estadístico de prueba es t exp, que sustituimos en el intervalo de confianza por\(\mu\)
\[\mu = \overline{X} \pm \frac {t_\text{exp} s} {\sqrt{n}} \nonumber \]
Reordenando esta ecuación y resolviendo\(t_\text{exp}\)
\[t_\text{exp} = \frac {|\mu - \overline{X}| \sqrt{n}} {s} \nonumber \]
da el valor para\(t_\text{exp}\) cuando\(\mu\) está en el borde derecho o el borde izquierdo del intervalo de confianza de la muestra (Figura\(\PageIndex{24a}\)).
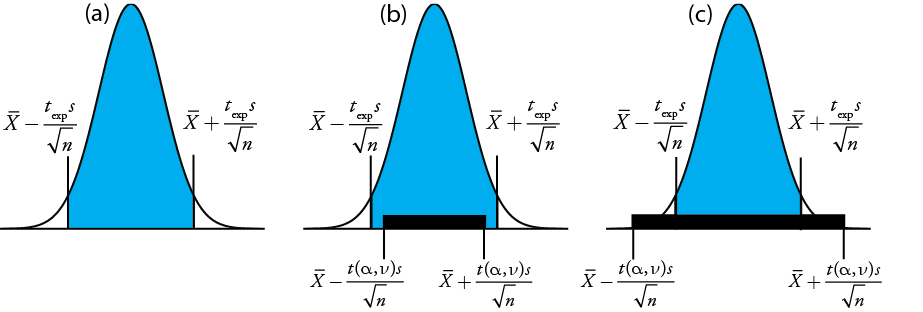
Para determinar si debemos retener o rechazar la hipótesis nula, comparamos el valor de t exp con un valor crítico,\(t(\alpha, \nu)\), donde\(\alpha\) está el nivel de confianza y\(\nu\) es los grados de libertad para la muestra. El valor crítico\(t(\alpha, \nu)\) define el mayor intervalo de confianza explicado por error indeterminado. Si\(t_\text{exp} > t(\alpha, \nu)\), entonces el intervalo de confianza de nuestra muestra es mayor que el explicado por errores indeterminados (Figura\(\PageIndex{24}\) b). En este caso, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Si\(t_\text{exp} \leq t(\alpha, \nu)\), entonces el intervalo de confianza de nuestra muestra es menor que el explicado por un error indeterminado, y conservamos la hipótesis nula (Figura\(\PageIndex{24}\) c). Ejemplo\(\PageIndex{24}\) proporciona una aplicación típica de esta prueba de significancia, la cual se conoce como una prueba t de\(\overline{X}\) a\(\mu\). Encontrará valores para\(t(\alpha, \nu)\) en el Apéndice 3.
Antes de determinar la cantidad de Na 2 CO 3 en una muestra, decide verificar su procedimiento analizando una muestra estándar que es 98.76% w/w Na 2 CO 3. Cinco determinaciones replicadas del% p/p de Na 2 CO 3 en el estándar dan los siguientes resultados
\(98.71 \% \quad 98.59 \% \quad 98.62 \% \quad 98.44 \% \quad 98.58 \%\)
Utilizando\(\alpha = 0.05\), ¿hay alguna evidencia de que el análisis está dando resultados inexactos?
Solución
La media y la desviación estándar para los cinco ensayos son
\[\overline{X} = 98.59 \quad \quad \quad s = 0.0973 \nonumber \]
Debido a que no hay razón para creer que los resultados para el estándar deben ser mayores o menores que\(\mu\), una prueba t de dos colas es apropiada. La hipótesis nula y la hipótesis alternativa son
\[H_0 \text{: } \overline{X} = \mu \quad \quad \quad H_\text{A} \text{: } \overline{X} \neq \mu \nonumber \]
El estadístico de prueba, t exp, es
\[t_\text{exp} = \frac {|\mu - \overline{X}|\sqrt{n}} {2} = \frac {|98.76 - 98.59| \sqrt{5}} {0.0973} = 3.91 \nonumber \]
El valor crítico para t (0.05, 4) del Apéndice 3 es 2.78. Dado que t exp es mayor que t (0.05, 4), rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Al nivel de confianza del 95% la diferencia entre\(\overline{X}\) y\(\mu\) es demasiado grande para ser explicada por fuentes indeterminadas de error, lo que sugiere que existe una fuente determinada de error que afecta el análisis.
Hay otra manera de interpretar el resultado de esta prueba t. Sabiendo que t exp es 3.91 y que hay 4 grados de libertad, utilizamos el Apéndice 3 para estimar el valor de\(\alpha\) que corresponde a una t (\(\alpha\), 4) de 3.91. Del Apéndice 3, t (0.02, 4) es 3.75 y t (0.01, 4) es 4.60. Si bien podemos rechazar la hipótesis nula en el nivel de confianza del 98%, no podemos rechazarla en el nivel de confianza del 99%. Para una discusión sobre las ventajas de este enfoque, véase J. A. C. Sterne y G. D. Smith “Tamizar la evidencia, ¿qué hay de malo en las pruebas de significación?” BMJ 2001, 322, 226—231.
Anteriormente hicimos el punto de que debemos tener precaución cuando interpretamos el resultado de un análisis estadístico. Seguiremos volviendo a este punto porque es importante. Habiendo determinado que un resultado es inexacto, como hicimos en Ejemplo\(\PageIndex{3}\), el siguiente paso es identificar y corregir el error. Sin embargo, antes de invertir tiempo y dinero en esto, primero debemos examinar críticamente nuestros datos. Por ejemplo, cuanto menor sea el valor de s, mayor será el valor de t exp. Si la desviación estándar para nuestro análisis es poco realista, entonces la probabilidad de un error tipo 2 aumenta. Incluir algunos análisis replicados adicionales del estándar y reevaluar la prueba t puede fortalecer nuestra evidencia de un error determinado, o puede mostrarnos que no hay evidencia de un error determinado.
Comparando\(s^2\) con\(\sigma^2\)
Si analizamos regularmente una muestra en particular, es posible que podamos establecer una varianza esperada,\(\sigma^2\), para el análisis. Este suele ser el caso, por ejemplo, en un laboratorio clínico que analiza cientos de muestras de sangre cada día. Algunos análisis replicados de una sola muestra dan una varianza muestral, s 2, cuyo valor puede o no diferir significativamente de\(\sigma^2\).
Podemos usar una prueba F para evaluar si una diferencia entre s 2 y\(\sigma^2\) es significativa. La hipótesis nula es\(H_0 \text{: } s^2 = \sigma^2\) y la hipótesis alternativa es\(H_\text{A} \text{: } s^2 \neq \sigma^2\). El estadístico de prueba para evaluar la hipótesis nula es F exp, que se da como
\[F_\text{exp} = \frac {s^2} {\sigma^2} \text{ if } s^2 > \sigma^2 \text{ or } F_\text{exp} = \frac {\sigma^2} {s^2} \text{ if } \sigma^2 > s^2 \nonumber \]
dependiendo de si s 2 es mayor o menor que\(\sigma^2\). Esta forma de definir F exp asegura que su valor siempre sea mayor o igual a uno.
Si la hipótesis nula es verdadera, entonces F exp debería ser igual a uno; sin embargo, debido a errores indeterminados, F exp, suele ser mayor que uno. Un valor crítico,\(F(\alpha, \nu_\text{num}, \nu_\text{den})\), es el mayor valor de F exp que podemos atribuir al error indeterminado dado el nivel de significancia especificado,\(\alpha\), y los grados de libertad para la varianza en el numerador,\(\nu_\text{num}\), y la varianza en el denominador,\(\nu_\text{den}\). Los grados de libertad para s 2 es n — 1, donde n es el número de réplicas utilizadas para determinar la varianza de la muestra, y los grados de libertad para\(\sigma^2\) se define como infinito,\(\infty\). Los valores críticos de F para\(\alpha = 0.05\) se enumeran en el Apéndice 4 para las pruebas F de una cola y dos colas.
El proceso de un fabricante para analizar tabletas de aspirina tiene una varianza conocida de 25. Se selecciona una muestra de 10 comprimidos de aspirina y se analiza para determinar la cantidad de aspirina, dando los siguientes resultados en mg de aspirina/comprimido.
\(254 \quad 249 \quad 252 \quad 252 \quad 249 \quad 249 \quad 250 \quad 247 \quad 251 \quad 252\)
Determinar si hay evidencia de una diferencia significativa entre la varianza de la muestra y la varianza esperada en\(\alpha = 0.05\).
Solución
La varianza para la muestra de 10 comprimidos es de 4.3. La hipótesis nula y las hipótesis alternativas son
\[H_0 \text{: } s^2 = \sigma^2 \quad \quad \quad H_\text{A} \text{: } s^2 \neq \sigma^2 \nonumber \]
y el valor para F exp es
\[F_\text{exp} = \frac {\sigma^2} {s^2} = \frac {25} {4.3} = 5.8 \nonumber \]
El valor crítico para F (0.05,\(\infty\), 9) del Apéndice 4 es 3.333. Dado que F exp es mayor que F (0.05,\(\infty\), 9), rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que existe una diferencia significativa entre la varianza de la muestra y la varianza esperada. Una explicación de la diferencia podría ser que las tabletas de aspirina no se seleccionaron al azar.
Comparación de varianzas para dos muestras
Podemos extender la prueba F para comparar las varianzas para dos muestras, A y B, reescribiendo nuestra ecuación para F exp como
\[F_\text{exp} = \frac {s_A^2} {s_B^2} \nonumber \]
definiendo A y B de manera que el valor de F exp sea mayor o igual a 1.
La siguiente tabla muestra los resultados de dos experimentos para determinar la masa de un centavo circulante de Estados Unidos. Determinar si existe una diferencia en las varianzas de estos análisis en\(\alpha = 0.05\).
| Primer experimento | Segundo Experimento | ||
|---|---|---|---|
| Penny | Masa (g) | Penny | Masa (g) |
| 1 | 3.080 | 1 | 3.052 |
| 2 | 3.094 | 2 | 3.141 |
| 3 | 3.107 | 3 | 3.083 |
| 4 | 3.056 | 4 | 3.083 |
| 5 | 3.112 | 5 | 3.048 |
| 6 | 3.174 | ||
| 7 | 3.198 | ||
Solución
Las desviaciones estándar para los dos experimentos son 0.051 para el primer experimento (A) y 0.037 para el segundo experimento (B). Las hipótesis nulas y alternativas son
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_\text{A} \text{: } s_A^2 \neq s_B^2 \nonumber \]
y el valor de F exp es
\[F_\text{exp} = \frac {s_A^2} {s_B^2} = \frac {(0.051)^2} {(0.037)^2} = \frac {0.00260} {0.00137} = 1.90 \nonumber \]
Del Apéndice 4 el valor crítico para F (0.05, 6, 4) es 9.197. Debido a que F exp < F (0.05, 6, 4), conservamos la hipótesis nula. No hay evidencia que sugiera\(\alpha = 0.05\) que la diferencia en las varianzas sea significativa.
Comparación de medias para dos muestras
Tres factores influyen en el resultado de un análisis: el método, la muestra y el analista. Podemos estudiar la influencia de estos factores mediante la realización de experimentos en los que cambiamos un factor mientras mantenemos constantes los otros factores. Por ejemplo, para comparar dos métodos analíticos podemos hacer que el mismo analista aplique cada método a la misma muestra y luego examine las medias resultantes. De manera similar, podemos diseñar experimentos para comparar dos analistas o comparar dos muestras.
Antes de considerar las pruebas de significancia para comparar las medias de dos muestras, necesitamos entender la diferencia entre los datos desapareados y los datos emparejados. Esta es una distinción crítica y aprender a distinguir entre estos dos tipos de datos es importante. Aquí hay dos ejemplos simples que resaltan la diferencia entre los datos no emparejados y los datos emparejados. En cada ejemplo el objetivo es comparar dos balanzas pesando centavos.
- Ejemplo 1: Recolectamos 10 peniques y pesamos cada centavo en cada saldo. Este es un ejemplo de datos emparejados porque usamos los mismos 10 centavos para evaluar cada saldo.
- Ejemplo 2: Recolectamos 10 centavos y los dividimos en dos grupos de cinco centavos cada uno. Pesamos los centavos en el primer grupo en una balanza y pesamos el segundo grupo de centavos en la otra balanza. Tenga en cuenta que no se pesa ningún centavo en ambas balanzas. Este es un ejemplo de datos no emparejados porque evaluamos cada saldo usando una muestra diferente de centavos.
En ambos ejemplos se extrajeron muestras de 10 centavos de una misma población; la diferencia es cómo muestreamos esa población. Aprenderemos por qué esta distinción es importante cuando revisamos la prueba de significancia para datos pareados; primero, sin embargo, presentamos la prueba de significancia para datos no apareados.
Una prueba simple para determinar si los datos están emparejados o no emparejados es observar el tamaño de cada muestra. Si las muestras son de diferente tamaño, entonces los datos deben estar desapareados. Lo contrario no es cierto. Si dos muestras son de igual tamaño, pueden estar emparejadas o desapareadas.
Datos no emparejados
Considera dos análisis, A y B, con medias de\(\overline{X}_A\) y\(\overline{X}_B\), y desviaciones estándar de s A y s B. Los intervalos de confianza para\(\mu_A\) y para\(\mu_B\) son
\[\mu_A = \overline{X}_A \pm \frac {t s_A} {\sqrt{n_A}} \nonumber \]
\[\mu_B = \overline{X}_B \pm \frac {t s_B} {\sqrt{n_B}} \nonumber \]
donde n A y n B son los tamaños de muestra para A y para B. Nuestra hipótesis nula,\(H_0 \text{: } \mu_A = \mu_B\), es que cualquier diferencia entre\(\mu_A\) y\(\mu_B\) es el resultado de errores indeterminados que afectan los análisis. La hipótesis alternativa,\(H_A \text{: } \mu_A \neq \mu_B\), es que la diferencia entre\(\mu_A\) y\(\mu_B\) es demasiado grande para ser explicada por error indeterminado.
Para derivar una ecuación para t exp, asumimos que\(\mu_A\) es igual\(\mu_B\) y combinamos las ecuaciones para los dos intervalos de confianza
\[\overline{X}_A \pm \frac {t_\text{exp} s_A} {\sqrt{n_A}} = \overline{X}_B \pm \frac {t_\text{exp} s_B} {\sqrt{n_B}} \nonumber \]
Resolviendo\(|\overline{X}_A - \overline{X}_B|\) y usando una propagación de la incertidumbre, da
\[|\overline{X}_A - \overline{X}_B| = t_\text{exp} \times \sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}} \nonumber \]
Por último, resolvemos para t exp
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {\sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}}} \nonumber \]
y compararlo con un valor crítico,\(t(\alpha, \nu)\), donde\(\alpha\) está la probabilidad de un error tipo 1, y\(\nu\) es los grados de libertad.
Hasta el momento nuestro desarrollo de esta prueba t es similar al de comparar\(\overline{X}\) con\(\mu\), y sin embargo no tenemos suficiente información para evaluar la prueba t. ¿Ves el problema? Con dos conjuntos de datos independientes no está claro cuántos grados de libertad tenemos.
Supongamos que las varianzas\(s_A^2\) y\(s_B^2\) proporcionan estimaciones de las mismas\(\sigma^2\). En este caso podemos sustituir\(s_A^2\) y\(s_B^2\) con una varianza agrupada,\(s_\text{pool}^2\), esa es una mejor estimación para la varianza. Por lo tanto, nuestra ecuación para\(t_\text{exp}\) se convierte
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool} \times \sqrt{\frac {1} {n_A} + \frac {1} {n_B}}} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool}} \times \sqrt{\frac {n_A n_B} {n_A + n_B}} \nonumber \]
donde s pool, la desviación estándar agrupada, es
\[s_\text{pool} = \sqrt{\frac {(n_A - 1) s_A^2 + (n_B - 1)s_B^2} {n_A + n_B - 2}} \nonumber \]
El denominador de esta ecuación nos muestra que los grados de libertad para una desviación estándar agrupada son\(n_A + n_B - 2\), que también son los grados de libertad para la prueba t. Tenga en cuenta que perdemos dos grados de libertad porque los cálculos para\(s_A^2\) y\(s_B^2\) requieren el cálculo previo de\(\overline{X}_A\) amd\(\overline{X}_B\).
Entonces, ¿cómo se determina si está bien agrupar las varianzas? Use una prueba F.
Si\(s_A^2\) y\(s_B^2\) son significativamente diferentes, entonces calculamos t exp usando la siguiente ecuación. En este caso, encontramos los grados de libertad utilizando la siguiente ecuación imponente.
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A + 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B + 1}} - 2 \nonumber \]
Debido a que los grados de libertad deben ser un entero, redondeamos al entero más cercano el valor de\(\nu\) obtenido de esta ecuación.
La ecuación anterior para los grados de libertad es de Miller, J.C.; Miller, J.N. Statistics for Analytical Chemistry, 2nd Ed., Ellis-Horward: Chichester, UK, 1988. En la 6ª Edición, los autores señalan que se han sugerido varias ecuaciones diferentes para el número de grados de libertad para t cuando s A y s B difieren, reflejando el hecho de que la determinación de grados de libertad es una aproximación. Una ecuación alternativa, que es utilizada por paquetes de software estadístico, como R, Minitab, Excel, es
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A - 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B - 1}} = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {s_A^4} {n_A^2(n_A - 1)} + \frac {s_B^4} {n_B^2(n_B - 1)}} \nonumber \]
Para problemas típicos de la química analítica, los grados de libertad calculados son razonablemente insensibles a la elección de la ecuación.
Independientemente de si cómo calculamos t exp, rechazamos la hipótesis nula si t exp es mayor que\(t(\alpha, \nu)\) y conservamos la hipótesis nula si t exp es menor o igual a\(t(\alpha, \nu)\).
Ejemplo\(\PageIndex{3}\) proporciona resultados para dos experimentos para determinar la masa de un penique circulante de Estados Unidos. Determinar si existe una diferencia en las medias de estos análisis en\(\alpha = 0.05\).
Solución
Primero usamos una prueba F para determinar si podemos agrupar las varianzas. Completamos este análisis en Ejemplo\(\PageIndex{5}\), no encontrando evidencia de una diferencia significativa, lo que significa que podemos agrupar las desviaciones estándar, obteniendo
\[s_\text{pool} = \sqrt{\frac {(7 - 1)(0.051)^2 + (5 - 1)(0.037)^2} {7 + 5 - 2}} = 0.0459 \nonumber \]
con 10 grados de libertad. Para comparar las medias utilizamos las siguientes hipótesis nulas e hipótesis alternativas
\[H_0 \text{: } \mu_A = \mu_B \quad \quad \quad H_A \text{: } \mu_A \neq \mu_B \nonumber \]
Debido a que estamos usando la desviación estándar agrupada, calculamos t exp como
\[t_\text{exp} = \frac {|3.117 - 3.081|} {0.0459} \times \sqrt{\frac {7 \times 5} {7 + 5}} = 1.34 \nonumber \]
El valor crítico para t (0.05, 10), del Apéndice 3, es 2.23. Debido a que t exp es menor que t (0.05, 10) conservamos la hipótesis nula. Porque no\(\alpha = 0.05\) tenemos evidencia de que los dos juegos de centavos sean significativamente diferentes.
Un método para determinar el% w/w de Na 2 CO 3 en la ceniza de sosa es usar una titulación ácido-base. Cuando dos analistas analizan la misma muestra de carbonato de sodio obtienen los resultados que aquí se muestran.
Analista A:\(86.82 \% \quad 87.04 \% \quad 86.93 \% \quad 87.01 \% \quad 86.20 \% \quad 87.00 \%\)
Analista B:\(81.01 \% \quad 86.15 \% \quad 81.73 \% \quad 83.19 \% \quad 80.27 \% \quad 83.93 \% \quad\)
Determinar si la diferencia en los valores medios es significativa en\(\alpha = 0.05\).
Solución
Comenzamos reportando la media y desviación estándar para cada analista.
\[\overline{X}_A = 86.83\% \quad \quad s_A = 0.32\% \nonumber \]
\[\overline{X}_B = 82.71\% \quad \quad s_B = 2.16\% \nonumber \]
Para determinar si podemos usar una desviación estándar agrupada, primero completamos una prueba F usando las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_A \text{: } s_A^2 \neq s_B^2 \nonumber \]
Calculando F exp, obtenemos un valor de
\[F_\text{exp} = \frac {(2.16)^2} {(0.32)^2} = 45.6 \nonumber \]
Debido a que F exp es mayor que el valor crítico de 7.15 para F (0.05, 5, 5) del Apéndice 4, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que existe una diferencia significativa entre las varianzas; así, no podemos calcular un estándar agrupado desviación.
Para comparar las medias de los dos analistas utilizamos las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } \overline{X}_A = \overline{X}_B \quad \quad \quad H_A \text{: } \overline{X}_A \neq \overline{X}_B \nonumber \]
Debido a que no podemos juntar las desviaciones estándar, calculamos t exp como
\[t_\text{exp} = \frac {|86.83 - 82.71|} {\sqrt{\frac {(0.32)^2} {6} + \frac {(2.16)^2} {6}}} = 4.62 \nonumber \]
y calcular los grados de libertad como
\[\nu = \frac {\left( \frac {(0.32)^2} {6} + \frac {(2.16)^2} {6} \right)^2} {\frac {\left( \frac {(0.32)^2} {6} \right)^2} {6 + 1} + \frac {\left( \frac {(2.16)^2} {6} \right)^2} {6 + 1}} - 2 = 5.3 \approx 5 \nonumber \]
Del Apéndice 3, el valor crítico para t (0.05, 5) es 2.57. Debido a que t exp es mayor que t (0.05, 5) rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que las medias para los dos analistas son significativamente diferentes en\(\alpha = 0.05\).
Datos emparejados
Supongamos que estamos evaluando un nuevo método para monitorear las concentraciones de glucosa en sangre en pacientes. Una parte importante de la evaluación de un nuevo método es compararlo con un método establecido. ¿Cuál es la mejor manera de recopilar datos para este estudio? Debido a que la variación en los niveles de glucosa en sangre entre los pacientes es grande, es posible que no podamos detectar una diferencia pequeña pero significativa entre los métodos si utilizamos diferentes pacientes para recopilar datos para cada método. Utilizando datos pareados, en los que analizamos la sangre de cada paciente utilizando ambos métodos, evita que una gran varianza dentro de una población afecte negativamente a una prueba t de medias.
Los niveles típicos de glucosa en sangre para la mayoría de los individuos no diabéticos oscilan entre 80—120 mg/dL (4.4—6.7 mM), elevándose a 140 mg/dL (7.8 mM) poco después de comer. Los niveles más altos son comunes en individuos que son prediabéticos o diabéticos.
Cuando usamos datos pareados primero calculamos las diferencias individuales, d i, entre los resykts emparejados de cada muestra. Usando estas diferencias individuales, calculamos entonces la diferencia promedio,\(\overline{d}\), y la desviación estándar de las diferencias, s d. La hipótesis nula,\(H_0 \text{: } d = 0\), es que no hay diferencia entre las dos muestras, y la hipótesis alternativa,\(H_A \text{: } d \neq 0\), es que la diferencia entre las dos muestras es significativa.
El estadístico de prueba, t exp, se deriva de un intervalo de confianza alrededor\(\overline{d}\)
\[t_\text{exp} = \frac {|\overline{d}| \sqrt{n}} {s_d} \nonumber \]
donde n es el número de muestras emparejadas. Como es cierto para otras formas de la prueba t, comparamos t exp con\(t(\alpha, \nu)\), donde los grados de libertad,\(\nu\), es n — 1. Si t exp es mayor que\(t(\alpha, \nu)\), entonces rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Conservamos la hipótesis nula si t exp es menor o igual a t (a, o). Esto se conoce como prueba t pareada.
Marecek et. al. desarrollaron un nuevo método electroquímico para la determinación rápida de la concentración del antibiótico monensina en cubas de fermentación [Marecek, V.; Janchenova, H.; Brezina, M.; Betti, M. Anal. Chim. Acta 1991, 244, 15—19]. El método estándar para el análisis es una prueba de actividad microbiológica, que es difícil de completar y requiere mucho tiempo. Se recolectaron muestras de las cubas de fermentación en diversos momentos durante la producción y se analizó la concentración de monensina mediante ambos métodos. Los resultados, en partes por mil (ppt), se reportan en la siguiente tabla.
| Muestra | Microbiológicos | Electroquímica |
|---|---|---|
| 1 | 129.5 | 132.3 |
| 2 | 89.6 | 91.0 |
| 3 | 76.6 | 73.6 |
| 4 | 52.2 | 58.2 |
| 5 | 110.8 | 104.2 |
| 6 | 50.4 | 49.9 |
| 7 | 72.4 | 82.1 |
| 8 | 141.4 | 154.1 |
| 9 | 75.0 | 73.4 |
| 10 | 34.1 | 38.1 |
| 11 | 60.3 | 60.1 |
¿Hay una diferencia significativa entre los métodos en\(\alpha = 0.05\)?
Solución
La adquisición de muestras durante un período prolongado de tiempo introduce un cambio sustancial dependiente del tiempo en la concentración de monensina. Debido a que la variación en la concentración entre muestras es tan grande, utilizamos una prueba t pareada con las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } \overline{d} = 0 \quad \quad \quad H_A \text{: } \overline{d} \neq 0 \nonumber \]
Definir la diferencia entre los métodos como
\[d_i = (X_\text{elect})_i - (X_\text{micro})_i \nonumber \]
calculamos la diferencia para cada muestra.
| muestra | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| \(d_i\) | 2.8 | 1.4 | —3.0 | 6.0 | —6.6 | —0.5 | 9.7 | 12.7 | —1.6 | 4.0 | —0.2 |
La media y la desviación estándar para las diferencias son, respectivamente, 2.25 ppt y 5.63 ppt. El valor de t exp es
\[t_\text{exp} = \frac {|2.25| \sqrt{11}} {5.63} = 1.33 \nonumber \]
que es menor que el valor crítico de 2.23 para t (0.05, 10) del Apéndice 3. Conservamos la hipótesis nula y no encontramos evidencia de una diferencia significativa en los métodos en\(\alpha = 0.05\).
Un requisito importante para una prueba t pareada es que los errores determinados e indeterminados que afectan el análisis deben ser independientes de la concentración del analito. Si este no es el caso, entonces una muestra con una concentración inusualmente alta de analito tendrá un d i inusualmente grande. Incluir esta muestra en el cálculo de\(\overline{d}\) y s d da una estimación sesgada para la media esperada y la desviación estándar. Esto rara vez es un problema para muestras que abarcan un rango limitado de concentraciones de analitos, como las de Ejemplo\(\PageIndex{6}\) o Ejercicio\(\PageIndex{8}\). Sin embargo, cuando los datos emparejados abarcan un amplio rango de concentraciones, la magnitud de las fuentes de error determinadas e indeterminadas puede no ser independiente de la concentración del analito; cuando es verdad, una prueba t pareada puede dar resultados engañosos porque los datos emparejados con el mayor absoluto los errores determinados e indeterminados dominarán\(\overline{d}\). En esta situación un análisis de regresión, que es el tema del siguiente capítulo, es el método más apropiado para comparar los datos.
Vale la pena examinar más de cerca la importancia de distinguir entre datos emparejados y desapareados. Los siguientes son datos de algunos trabajos que completé con un colega en el que estábamos analizando la concentración de Zn en el lago Erie en la interfaz aire-agua y la interfaz sedimento-agua.
| sitio de muestra | ppm de Zn en la interfaz aire-agua | ppm de Zn en la interfaz sedimento-agua |
| 1 | 0.430 | 0.415 |
| 2 | 0.266 | 0.238 |
| 3 | 0.457 | 0.390 |
| 4 | 0.531 | 0.410 |
| 5 | 0.707 | 0.605 |
| 6 | 0.716 | 0.609 |
La media y la desviación estándar para las ppm de Zn en la interfaz aire-agua son 0.5178 ppm y 0.01732 ppm, y la media y la desviación estándar para las ppm Zn en la interfaz sedimento-agua son 0.4445 ppm y 0.1418 ppm. Podemos utilizar estos valores para dibujar distribuciones normales tanto para dejar las medias como las desviaciones estándar para las muestras,\(\overline{X}\) y\(s\), servir como estimaciones para las medias y las desviaciones estándar para la población,\(\mu\) y\(\sigma\). Como vemos en la siguiente figura
las dos distribuciones se superponen fuertemente, lo que sugiere que una prueba t de sus medias no es probable que encuentre evidencia de una diferencia. Y sin embargo, también vemos que para cada sitio, la concentración de Zn en la interfaz sedimento-agua es menor que en la interfaz aire-agua. En este caso, la diferencia entre la concentración de Zn en sitios individuales es suficientemente grande como para enmascara nuestra capacidad de ver la diferencia entre las dos interfaces.
Si tomamos las diferencias entre las interfaces aire-agua y sedimento-agua, tenemos valores de 0.015, 0.028, 0.067, 0.121, 0.102 y 0.107 ppm de Zn, con una media de 0.07333 ppm de Zn y una desviación estándar de 0.04410 ppm de Zn. Superposición de las tres distribuciones normales
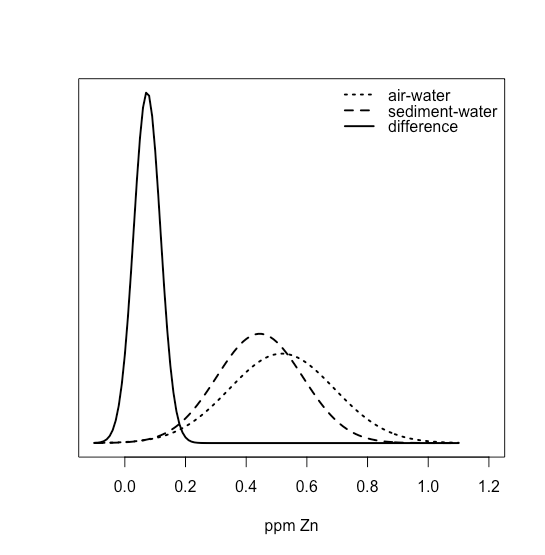
muestra claramente que la mayor parte de la distribución normal para las diferencias se encuentra por encima de cero, sugiriendo que una prueba t podría mostrar evidencia de que la diferencia es significativa.
valores atípicos
Tabla\(\PageIndex{11}\) proporciona un conjunto de datos más dando las masas para una muestra de centavos. ¿Se nota algo inusual en estos datos? De los 100 centavos incluidos en nuestra tabla anterior, ningún centavo tiene una masa inferior a 3 g. En esta tabla, sin embargo, la masa de un centavo es inferior a 3 g. Podríamos preguntarnos si la masa de este centavo es tan diferente de los otros centavos que está en error.
| 3.067 | 2.514 | 3.094 |
| 3.049 | 3.048 | 3.109 |
| 3.039 | 3.079 | 3.102 |
Una medición que no es consistente con otras mediciones se denomina valor atípico. Un valor atípico puede existir por muchas razones: el valor atípico podría pertenecer a una población diferente
¿Es esto un centavo canadiense?
o el valor atípico podría ser una muestra contaminada o alterada
¿El centavo está dañado o inusualmente sucio?
o el valor atípico puede resultar de un error en el análisis
¿Nos olvidamos de tara la balanza?
Independientemente de su fuente, la presencia de un valor atípico compromete cualquier análisis significativo de nuestros datos. Hay muchas pruebas de significación que podemos usar para identificar un posible valor atípico, tres de las cuales presentamos aquí.
Prueba Q de Dixon
Una de las pruebas de significancia más comunes para identificar un valor atípico es la prueba Q de Dixon. La hipótesis nula es que no hay valores atípicos, y la hipótesis alternativa es que hay un valor atípico. La prueba Q compara la brecha entre el valor atípico sospechoso y su vecino numérico más cercano con el rango de todo el conjunto de datos (Figura\(\PageIndex{25}\)).
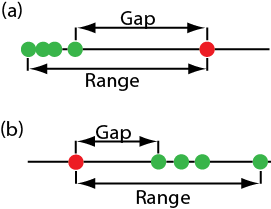
El estadístico de prueba, Q exp, es
\[Q_\text{exp} = \frac {\text{gap}} {\text{range}} = \frac {|\text{outlier's value} - \text{nearest value}|} {\text{largest value} - \text{smallest value}} \nonumber \]
Esta ecuación es apropiada para evaluar un único valor atípico. Otras formas de la prueba Q de Dixon permiten su extensión a la detección de múltiples valores atípicos [Rorabacher, D. B. Anal. Chem. 1991, 63, 139—146].
El valor de Q exp se compara con un valor crítico,\(Q(\alpha, n)\), donde\(\alpha\) está la probabilidad de que rechacemos un punto de datos válido (un error tipo 1) y n es el número total de puntos de datos. Para proteger contra el rechazo de un punto de datos válido, generalmente aplicamos la prueba Q de dos colas más conservadora, aunque el valor atípico posible es el valor más pequeño o el mayor en el conjunto de datos. Si Q exp es mayor que\(Q(\alpha, n)\), entonces rechazamos la hipótesis nula y podemos excluir el valor atípico. Conservamos el posible valor atípico cuando Q exp es menor o igual a\(Q(\alpha, n)\). Tabla\(\PageIndex{12}\) proporciona valores\(Q(\alpha, n)\) para un conjunto de datos que tiene 3—10 valores. Una tabla más extensa se encuentra en el Apéndice 5. Valores para\(Q(\alpha, n)\) asumir una distribución normal subyacente.
| n | Q (0.05, n) |
|---|---|
| 3 | 0.970 |
| 4 | 0.829 |
| 5 | 0.710 |
| 6 | 0.625 |
| 7 | 0.568 |
| 8 | 0.526 |
| 9 | 0.493 |
| 10 | 0.466 |
Prueba de Grubb
Si bien la prueba Q de Dixon es un método común para evaluar valores atípicos, ya no es favorecida por la Organización Internacional de Normalización (ISO), que recomienda la prueba de Grubb. Existen varias versiones de la prueba de Grubb dependiendo del número de posibles valores atípicos. Aquí consideraremos el caso donde hay un solo presunto valor atípico.
Para obtener detalles sobre esta recomendación, consulte la Guía ISO de Normas Internacionales 5752-2 “Exactitud (veracidad y precisión) de los métodos y resultados de medición—Parte 2: métodos básicos para la determinación de la repetibilidad y reproducibilidad de un método de medición estándar”, 1994.
El estadístico de prueba para la prueba de Grubb, G exp, es la distancia entre la media de la muestra\(\overline{X}\), y el valor atípico potencial\(X_\text{out}\), en términos de la desviación estándar de la muestra, s.
\[G_\text{exp} = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber \]
Comparamos el valor de G exp con un valor crítico\(G(\alpha, n)\), donde\(\alpha\) está la probabilidad de que rechacemos un punto de datos válido y n es el número de puntos de datos en la muestra. Si G exp es mayor que\(G(\alpha, n)\), entonces podemos rechazar el punto de datos como un valor atípico, de lo contrario conservamos el punto de datos como parte de la muestra. \(\PageIndex{13}\)La tabla proporciona valores para G (0.05, n) para una muestra que contiene 3—10 valores. Una tabla más extensa se encuentra en el Apéndice 6. Valores para\(G(\alpha, n)\) asumir una distribución normal subyacente.
| n | G (0.05, n) |
|---|---|
| 3 | 1.115 |
| 4 | 1.481 |
| 5 | 1.715 |
| 6 | 1.887 |
| 7 | 2.020 |
| 8 | 2.126 |
| 9 | 2.215 |
| 10 | 2.290 |
Criterio de Chauvenet
Nuestro método final para identificar un valor atípico es el criterio de Chauvenet. A diferencia de la prueba Q de Dixon y la prueba de Grubb, puedes aplicar este método a cualquier distribución siempre que sepas cómo calcular la probabilidad de un resultado en particular. El criterio de Chauvenet establece que podemos rechazar un punto de datos si la probabilidad de obtener el valor del punto de datos es menor que\((2n^{-1})\), donde n es el tamaño de la muestra. Por ejemplo, si n = 10, un resultado con una probabilidad menor que\((2 \times 10)^{-1}\), o 0.05, se considera un valor atípico.
Para calcular la probabilidad de un valor atípico potencial, primero calculamos su desviación estandarizada, z
\[z = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber \]
donde\(X_\text{out}\) es el valor atípico potencial,\(\overline{X}\) es la media de la muestra y s es la desviación estándar de la muestra. Tenga en cuenta que esta ecuación es idéntica a la ecuación para G exp en la prueba de Grubb. Para una distribución normal, podemos encontrar la probabilidad de obtener un valor de z usando la tabla de probabilidad en el Apéndice 2.
La tabla\(\PageIndex{11}\) contiene las masas por nueve centavos circulantes de Estados Unidos. Una entrada, 2.514 g, parece ser un valor atípico. Determine si este centavo es un valor atípico usando una prueba Q, una prueba de Grubb y el criterio de Chauvenet. Para la prueba Q y la prueba de Grubb, vamos\(\alpha = 0.05\).
Solución
Para la prueba Q, el valor para\(Q_\text{exp}\) es
\[Q_\text{exp} = \frac {|2.514 - 3.039|} {3.109 - 2.514} = 0.882 \nonumber \]
De la Tabla\(\PageIndex{12}\), el valor crítico para Q (0.05, 9) es 0.493. Debido a que Q exp es mayor que Q (0.05, 9), podemos suponer que el centavo con una masa de 2.514 g probablemente sea un valor atípico.
Para la prueba de Grubb primero necesitamos la media y la desviación estándar, que son 3.011 g y 0.188 g, respectivamente. El valor para G exp es
\[G_\text{exp} = \frac {|2.514 - 3.011|} {0.188} = 2.64 \nonumber \]
Usando Table\(\PageIndex{13}\), encontramos que el valor crítico para G (0.05, 9) es 2.215. Debido a que G exp es mayor que G (0.05, 9), podemos suponer que el centavo con una masa de 2.514 g probablemente es un valor atípico.
Para el criterio de Chauvenet, la probabilidad crítica es\((2 \times 9)^{-1}\), o 0.0556. El valor de z es el mismo que G exp, o 2.64. Usando el Apéndice 1, la probabilidad para z = 2.64 es 0.00415. Debido a que la probabilidad de obtener una masa de 0.2514 g es menor que la probabilidad crítica, podemos suponer que el centavo con una masa de 2.514 g probable es un valor atípico.
Debe tener precaución al usar una prueba de significancia para valores atípicos porque existe la posibilidad de que rechace un resultado válido. Además, debes evitar rechazar un valor atípico si lleva a una precisión mucho mejor de lo esperado en base a una propagación de la incertidumbre. Ante estas preocupaciones no es sorprendente que algunos estadísticos adviertan contra la eliminación de valores atípicos [Deming, W. E. Statistical Analysis of Data; Wiley: New York, 1943 (reeditado por Dover: New York, 1961); p. 171].
También puede adoptar un requisito más estricto para rechazar datos. Al usar la prueba de Grubb, por ejemplo, las pautas ISO 5752 sugieren retener un valor si la probabilidad de rechazarlo es mayor que\(\alpha = 0.05\), y marcar un valor como “rezagado” si la probabilidad de rechazarlo es entre\(\alpha = 0.05\) y\(\alpha = 0.01\). Un “rezagado” se retiene a menos que haya razones imperiosas para su rechazo. Los lineamientos recomiendan utilizar\(\alpha = 0.01\) como criterio mínimo para rechazar un posible valor atípico.
Por otro lado, las pruebas para detectar valores atípicos pueden proporcionar información útil si tratamos de entender la fuente del presunto valor atípico. Por ejemplo, el valor atípico en Table\(\PageIndex{11}\) representa un cambio significativo en la masa de un centavo (una disminución de aproximadamente 17% en la masa), que es el resultado de un cambio en la composición del centavo estadounidense. En 1982 la composición de un centavo estadounidense cambió de una aleación de latón que era 95% w/w Cu y 5% w/w Zn (con una masa nominal de 3.1 g), a un núcleo de zinc puro cubierto con cobre (con una masa nominal de 2.5 g) [Richardson, T. H. J. Chem. Educ. 1991, 68, 310—311]. Los centavos en Tabla\(\PageIndex{11}\), por lo tanto, se extrajeron de diferentes poblaciones.
Calibración de datos
Una curva de calibración es una de las herramientas más importantes en química analítica ya que nos permite determinar la concentración de un analito en una muestra midiendo la señal que genera cuando se coloca en un instrumento, como un espectrofotómetro. Para determinar la concentración del analito debemos conocer la relación entre la señal que medimos\(S\),, y la concentración del analito\(C_A\),, que podemos escribir como
\[S = k_A C_A + S_{blank} \nonumber \]
donde\(k_A\) está la sensibilidad de la curva de calibración y\(S_{blank}\) es la señal en ausencia de analito.
¿Cómo encontramos la mejor estimación para esta relación entre la señal y la concentración de analito? Cuando una curva de calibración es una línea recta, la representamos usando el siguiente modelo matemático
\[y = \beta_0 + \beta_1 x \nonumber \]
donde y es la señal medida del analito, S, y x es la concentración conocida del analito\(C_A\), en una serie de soluciones estándar. Las constantes\(\beta_0\) y\(\beta_1\) son, respectivamente, la intersección y esperada de la curva de calibración y su pendiente esperada. Debido a la incertidumbre en nuestras mediciones, lo mejor que podemos hacer es estimar valores para\(\beta_0\) y\(\beta_1\), que representamos como b 0 y b 1. El objetivo de un análisis de regresión lineal es determinar las mejores estimaciones para b 0 y b 1.
Regresión lineal no ponderada con errores en y
El método más común para completar una regresión lineal hace tres suposiciones:
- la diferencia entre nuestros datos experimentales y la línea de regresión calculada es el resultado de errores indeterminados que afectan a y
- cualquier error indeterminado que afecte y se distribuya normalmente
- que los errores indeterminados en y son independientes del valor de x
Debido a que asumimos que los errores indeterminados son los mismos para todos los estándares, cada estándar contribuye por igual en nuestra estimación de la pendiente y la intersección y. Por esta razón el resultado se considera una regresión lineal no ponderada.
El segundo supuesto generalmente es cierto debido al teorema del límite central, que consideramos anteriormente. La validez de los dos supuestos restantes es menos obvia y debes evaluarlos antes de aceptar los resultados de una regresión lineal. En particular la primera suposición siempre es sospechosa porque ciertamente hay algún error indeterminado en la medición de x. Cuando preparamos una curva de calibración, sin embargo, no es raro encontrar que la incertidumbre en la señal, S, es significativamente mayor que la incertidumbre en la concentración del analito,\(C_A\). En tales circunstancias el primer supuesto suele ser razonable.
Cómo funciona una regresión lineal
Para entender la lógica de una regresión lineal consideremos el ejemplo de la Figura\(\PageIndex{26}\), que muestra tres puntos de datos y dos posibles líneas rectas que podrían explicar razonablemente los datos. ¿Cómo decidimos qué tan bien estas líneas rectas se ajustan a los datos y cómo determinamos cuál, si alguna, es la mejor línea recta?
Centrémonos en la línea sólida de la Figura\(\PageIndex{26}\). La ecuación para esta línea es
\[\hat{y} = b_0 + b_1 x \nonumber \]
donde b 0 y b 1 son estimaciones para la intersección y y la pendiente, y\(\hat{y}\) es el valor predicho de y para cualquier valor de x. Porque suponemos que toda incertidumbre es el resultado de errores indeterminados en y, la diferencia entre y y\(\hat{y}\) para cada valor de x es el error residual, r, en nuestro modelo matemático.
\[r_i = (y_i - \hat{y}_i) \nonumber \]
La figura\(\PageIndex{27}\) muestra los errores residuales para los tres puntos de datos. Cuanto menor sea el error residual total, R, que definimos como
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \nonumber \]
mejor es el ajuste entre la línea recta y los datos. En un análisis de regresión lineal, buscamos valores de b 0 y b 1 que den el menor error residual total.
La razón para cuadrar los errores residuales individuales es evitar que un error residual positivo cancele un error residual negativo. Esto lo ha visto antes en las ecuaciones para las desviaciones estándar muestrales y poblacionales introducidas en el Capítulo 4. También se puede ver a partir de esta ecuación por qué a una regresión lineal se le llama a veces el método de mínimos cuadrados.
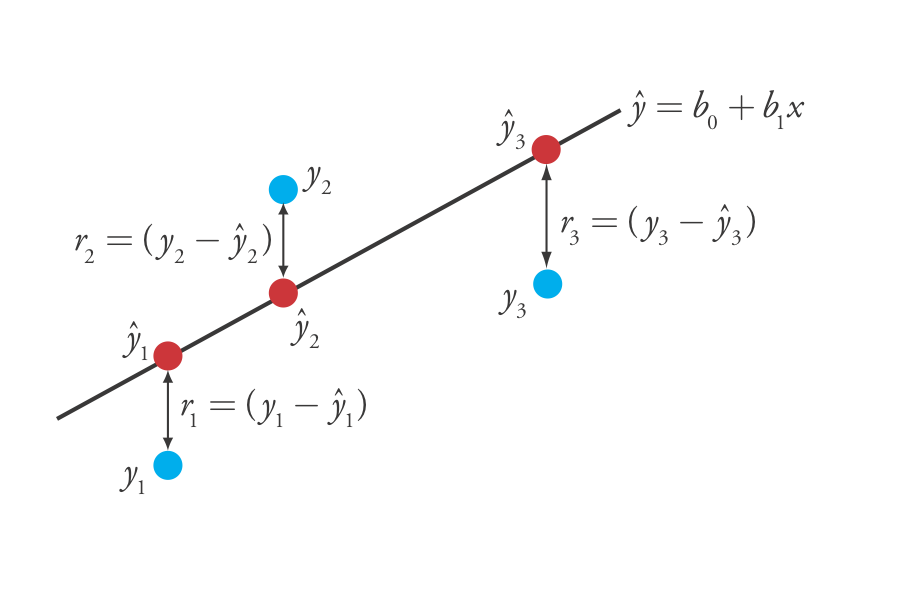
Encontrar la pendiente y la intersección y para el modelo de regresión
Aunque no desarrollaremos formalmente las ecuaciones matemáticas para un análisis de regresión lineal, se pueden encontrar las derivaciones en muchos textos estadísticos estándar [Véase, por ejemplo, Draper, N. R.; Smith, H. Applied Regression Analysis, 3a ed.; Wiley: New York, 1998]. La ecuación resultante para la pendiente, b 1, es
\[b_1 = \frac {n \sum_{i = 1}^{n} x_i y_i - \sum_{i = 1}^{n} x_i \sum_{i = 1}^{n} y_i} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2} \nonumber \]
y la ecuación para la intersección y, b 0, es
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \nonumber \]
Si bien estas ecuaciones parecen formidables, sólo es necesario evaluar las siguientes cuatro sumas
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber \]
Muchas calculadoras, hojas de cálculo y otros paquetes de software estadístico son capaces de realizar un análisis de regresión lineal basado en este modelo; consulte la Sección 8.5 para obtener detalles sobre cómo completar un análisis de regresión lineal usando R. Para fines ilustrativos, los cálculos necesarios se muestran en detalle en la siguiente ejemplo.
Utilizando los datos de calibración de la siguiente tabla, se determina la relación entre la señal\(y_i\), y la concentración del analito\(x_i\), utilizando una regresión lineal no ponderada.
Solución
Comenzamos configurando una tabla que nos ayude a organizar el cálculo.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (x_i y_i\) ">0.000 | \ (x_i^2\) ">0.000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (x_i y_i\) ">1.236 | \ (x_i^2\) ">0.010 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (x_i y_i\) ">4.966 | \ (x_i^2\) ">0.040 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (x_i y_i\) ">10.773 | \ (x_i^2\) ">0.090 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (x_i y_i\) ">19.516 | \ (x_i^2\) ">0.160 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (x_i y_i\) ">30.210 | \ (x_i^2\) ">0.250 |
Sumando los valores en cada columna da
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber \]
Sustituyendo estos valores en las ecuaciones para la pendiente y la intersección y da
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber \]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber \]
La relación entre la señal,\(S\), y la concentración del analito\(C_A\), por lo tanto, es
\[S = 120.71 \times C_A + 0.21 \nonumber \]
Por ahora mantenemos dos decimales para que coincidan con el número de decimales en la señal. La curva de calibración resultante se muestra en la Figura\(\PageIndex{28}\).
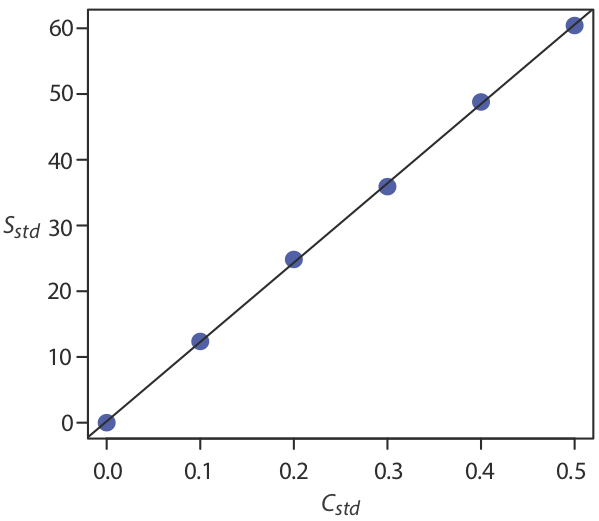
Incertidumbre en el modelo de regresión
Como vemos en la Figura\(\PageIndex{28}\), debido a errores indeterminados en la señal, la línea de regresión no pasa por el centro exacto de cada punto de datos. La desviación acumulada de nuestros datos de la línea de regresión —el error residual total— es proporcional a la incertidumbre en la regresión. Llamamos a esta incertidumbre la desviación estándar sobre la regresión, s r, que es igual a
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \nonumber \]
donde y i es el i-ésimo valor experimental, y\(\hat{y}_i\) es el valor correspondiente predicho por la ecuación de regresión\(\hat{y} = b_0 + b_1 x\). Tenga en cuenta que el denominador indica que nuestro análisis de regresión tiene n — 2 grados de libertad — perdemos dos grados de libertad porque utilizamos dos parámetros, la pendiente y la intersección y, para calcular\(\hat{y}_i\).
Una representación más útil de la incertidumbre en nuestro análisis de regresión es considerar el efecto de errores indeterminados en la pendiente, b 1, y la intersección y, b 0, que expresamos como desviaciones estándar.
\[s_{b_1} = \sqrt{\frac {n s_r^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2} {\sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
\[s_{b_0} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
Utilizamos estas desviaciones estándar para establecer intervalos de confianza para la pendiente esperada\(\beta_1\), y la intersección y esperada,\(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \nonumber \]
\[\beta_0 = b_0 \pm t s_{b_0} \nonumber \]
donde seleccionamos t para un nivel de significancia de\(\alpha\) y para n — 2 grados de libertad. Tenga en cuenta que estas ecuaciones no contienen el factor de\((\sqrt{n})^{-1}\) visto en los intervalos de confianza\(\mu\) porque el intervalo de confianza aquí se basa en una sola línea de regresión.
Calcular los intervalos de confianza del 95% para la pendiente y -intercepción a partir del Ejemplo\(\PageIndex{10}\).
Solución
Comenzamos calculando la desviación estándar sobre la regresión. Para ello debemos calcular las señales predichas,\(\hat{y}_i\), utilizando la pendiente y la intersección y del Ejemplo\(\PageIndex{10}\), y los cuadrados del error residual,\((y_i - \hat{y}_i)^2\). Usando el último estándar como ejemplo, encontramos que la señal predicha es
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber \]
y que el cuadrado del error residual es
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber \]
En la siguiente tabla se muestran los resultados de las seis soluciones.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) | \(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (\ hat {y} _i\) ">0.209 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0437 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (\ hat {y} _i\) ">12.280 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0064 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (\ hat {y} _i\) ">24.350 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.2304 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (\ hat {y} _i\) ">36.421 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.2611 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (\ hat {y} _i\) ">48.491 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0894 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (\ hat {y} _i\) ">60.562 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0202 |
Al sumar los datos de la última columna se obtiene el numerador en la ecuación para la desviación estándar sobre la regresión; así
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber \]
A continuación calculamos las desviaciones estándar para la pendiente y la intersección y. Los valores para los términos de suma son de Ejemplo\(\PageIndex{10}\).
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber \]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber \]
Finalmente, los intervalos de confianza del 95% (\(\alpha = 0.05\), 4 grados de libertad) para la pendiente y la intersección y son
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber \]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber \]
donde t (0.05, 4) del Apéndice 3 es 2.78. La desviación estándar sobre la regresión, s r, sugiere que la señal, S std, es precisa a un lugar decimal. Por esta razón reportamos la pendiente y la intersección y a un solo decimal.
Uso del modelo de regresión para determinar un valor para x Dado un valor para y
Una vez que tenemos nuestra ecuación de regresión, es fácil determinar la concentración de analito en una muestra. Cuando usamos una curva de calibración normal, por ejemplo, medimos la señal para nuestra muestra, S samp, y calculamos la concentración del analito, C A, usando la ecuación de regresión.
\[C_A = \frac {S_{samp} - b_0} {b_1} \nonumber \]
Lo menos obvio es cómo reportar un intervalo de confianza para C A que exprese la incertidumbre en nuestro análisis. Para calcular un intervalo de confianza necesitamos conocer la desviación estándar en la concentración del analito\(s_{C_A}\), que viene dada por la siguiente ecuación
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{S}_{samp} - \overline{S}_{std} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( C_{std_i} - \overline{C}_{std} \right)^2}} \nonumber \]
donde m es el número de réplicas que utilizamos para establecer la señal promedio de la muestra, S samp, n es el número de estándares de calibración, S std es la señal promedio para la calibración estándares, y\(C_{std_i}\) y\(\overline{C}_{std}\) son las concentraciones individuales y medias para los estándares de calibración. Conociendo el valor de\(s_{C_A}\), el intervalo de confianza para la concentración del analito es
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber \]
donde\(\mu_{C_A}\) está el valor esperado de C A en ausencia de errores determinados, y con el valor de t se basa en el nivel de confianza deseado y n — 2 grados de libertad.
Un examen minucioso de estas ecuaciones debería convencerle de que podemos disminuir la incertidumbre en la concentración predicha de analito,\(C_A\) si aumentamos el número de estándares\(n\),, aumentar el número de muestras replicadas que analizamos,\(m\), y si la señal promedio de la muestra, \(\overline{S}_{samp}\), es igual a la señal promedio para los estándares,\(\overline{S}_{std}\). Cuando sea práctico, debe planificar su curva de calibración para que S samp caiga en el medio de la curva de calibración. Para mayor información sobre estas ecuaciones de regresión ver (a) Miller, J. N. Analyst 1991, 116, 3—14; (b) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986, pp. 126-127; (c) Analytical Methods Committee” Incertidumbres en las concentraciones estimadas a partir de experimentos de calibración”, Informe Técnico de AMC, marzo de 2006.
La ecuación para la desviación estándar en la concentración del analito se escribe en términos de un experimento de calibración. Aquí se da una forma más general de la ecuación, escrita en términos de x e y.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
Tres análisis replicados para una muestra que contiene una concentración desconocida de analito, arroja valores para S samp de 29.32, 29.16 y 29.51 (unidades arbitrarias). Usando los resultados de Ejemplo\(\PageIndex{10}\) y Ejemplo\(\PageIndex{11}\), determinar la concentración del analito, C A, y su intervalo de confianza del 95%.
Solución
La señal promedio,\(\overline{S}_{samp}\), es 29.33, que, usando la pendiente y la intersección y del Ejemplo\(\PageIndex{10}\), da la concentración del analito como
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber \]
Para calcular la desviación estándar para la concentración del analito debemos determinar los valores para\(\overline{S}_{std}\) y para\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). El primero es solo la señal promedio para los estándares de calibración, que, utilizando los datos de la Tabla\(\PageIndex{10}\), es de 30.385. El cálculo\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) parece formidable, pero podemos simplificar su cálculo reconociendo que esta suma de cuadrados es el numerador en una ecuación de desviación estándar; así,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber \]
donde\(s_{C_{std}}\) está la desviación estándar para la concentración de analito en los estándares de calibración. Usando los datos de la Tabla\(\PageIndex{10}\) encontramos que\(s_{C_{std}}\) es 0.1871 y
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber \]
Sustituir valores conocidos en la ecuación para\(s_{C_A}\) da
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber \]
Finalmente, el intervalo de confianza del 95% para 4 grados de libertad es
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber \]
La figura\(\PageIndex{29}\) muestra la curva de calibración con curvas que muestran el intervalo de confianza del 95% para C A.
Evaluación de un modelo de regresión
Nunca se debe aceptar el resultado de un análisis de regresión lineal sin evaluar la validez del modelo. Quizás la forma más sencilla de evaluar un análisis de regresión es examinar los errores residuales. Como vimos anteriormente, el error residual para un único estándar de calibración, r i, es
\[r_i = (y_i - \hat{y}_i) \nonumber \]
Si el modelo de regresión es válido, entonces los errores residuales deben distribuirse aleatoriamente alrededor de un error residual promedio de cero, sin tendencia aparente hacia errores residuales menores o mayores (Figura\(\PageIndex{30a}\)). Tendencias como las de Figura\(\PageIndex{30b}\) y Figura\(\PageIndex{30c}\) proporcionan evidencia de que al menos uno de los supuestos del modelo es incorrecto. Por ejemplo, una tendencia hacia errores residuales mayores a concentraciones más altas, Figura\(\PageIndex{30b}\), sugiere que los errores indeterminados que afectan a la señal no son independientes de la concentración del analito. En la Figura\(\PageIndex{30c}\), los errores residuales no son aleatorios, lo que sugiere que no podemos modelar los datos usando una relación de línea recta. Los métodos de regresión para estos dos últimos casos se discuten en las siguientes secciones.
Usa tus resultados de Ejercicio\(\PageIndex{10}\) para construir una parcela residual y explicar su significado.
Solución
Para crear una gráfica residual, necesitamos calcular el error residual para cada estándar. La siguiente tabla contiene la información relevante.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) | \(y_i - \hat{y}_i\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.000 | \ (\ hat {y} _i\) ">0.0015 | \ (y_i -\ hat {y} _i\) ">—0.0015 |
| \ (x_i\) ">\(1.55 \times 10^{-3}\) | \ (y_i\) ">0.050 | \ (\ hat {y} _i\) ">0.0473 | \ (y_i -\ hat {y} _i\) ">0.0027 |
| \ (x_i\) ">\(3.16 \times 10^{-3}\) | \ (y_i\) ">0.093 | \ (\ hat {y} _i\) ">0.0949 | \ (y_i -\ hat {y} _i\) ">—0.0019 |
| \ (x_i\) ">\(4.74 \times 10^{-3}\) | \ (y_i\) ">0.143 | \ (\ hat {y} _i\) ">0.1417 | \ (y_i -\ hat {y} _i\) ">0.0013 |
| \ (x_i\) ">\(6.34 \times 10^{-3}\) | \ (y_i\) ">0.188 | \ (\ hat {y} _i\) ">0.1890 | \ (y_i -\ hat {y} _i\) ">—0.0010 |
| \ (x_i\) ">\(7.92 \times 10^{-3}\) | \ (y_i\) ">0.236 | \ (\ hat {y} _i\) ">0.2357 | \ (y_i -\ hat {y} _i\) ">0.0003 |
La siguiente figura muestra una gráfica de los errores residuales resultantes. Los errores residuales aparecen aleatorios, aunque sí alternan en signo, y no muestran ninguna dependencia significativa de la concentración del analito. En conjunto, estas observaciones sugieren que nuestro modelo de regresión es apropiado.
Regresión lineal ponderada con errores en y
Nuestro tratamiento de la regresión lineal a este punto asume que cualquier error indeterminado que afecte a y es independiente del valor de x. Si esta suposición es falsa, entonces debemos incluir la varianza para cada valor de y en nuestra determinación de la intersección y, b 0, y la pendiente, b 1; así
\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \nonumber \]
\[b_1 = \frac {n \sum_{i = 1}^{n} w_i x_i y_i - \sum_{i = 1}^{n} w_i x_i \sum_{i = 1}^{n} w_i y_i} {n \sum_{i =1}^{n} w_i x_i^2 - \left( \sum_{i = 1}^{n} w_i x_i \right)^2} \nonumber \]
donde w i es un factor de ponderación que da cuenta de la varianza en y i
\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \nonumber \]
y\(s_{y_i}\) es la desviación estándar para y i. En una regresión lineal ponderada, la contribución de cada par xy a la línea de regresión es inversamente proporcional a la precisión de y i; es decir, cuanto más preciso sea el valor de y, mayor será su contribución a la regresión.
Aquí se muestran datos para una estandarización externa en la que s std es la desviación estándar para la determinación de tres réplicas de la señal.
| \(C_{std}\)(unidades arbitrarias) | \(S_{std}\)(unidades arbitrarias) | \(s_{std}\) |
|---|---|---|
| \ (C_ {std}\) (unidades arbitrarias) ">0.000 | \ (S_ {std}\) (unidades arbitrarias) ">0.00 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.100 | \ (S_ {std}\) (unidades arbitrarias) ">12.36 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.200 | \ (S_ {std}\) (unidades arbitrarias) ">24.83 | \ (s_ {std}\) ">0.07 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.300 | \ (S_ {std}\) (unidades arbitrarias) ">35.91 | \ (s_ {std}\) ">0.13 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.400 | \ (S_ {std}\) (unidades arbitrarias) ">48.79 | \ (s_ {std}\) ">0.22 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.500 | \ (S_ {std}\) (unidades arbitrarias) ">60.42 | \ (s_ {std}\) ">0.33 |
Determinar la ecuación de la curva de calibración usando una regresión lineal ponderada. Al trabajar a través de este ejemplo, recuerde que x corresponde a C std, y que y corresponde a S std.
Solución
Comenzamos configurando una tabla para ayudar en el cálculo de los factores de ponderación.
| \(C_{std}\)(unidades arbitrarias) | \(S_{std}\)(unidades arbitrarias) | \(s_{std}\) | \((s_{y_i})^{-2}\) | \(w_i\) |
|---|---|---|---|---|
| \ (C_ {std}\) (unidades arbitrarias) ">0.000 | \ (S_ {std}\) (unidades arbitrarias) ">0.00 | \ (s_ {std}\) ">0.02 | \ ((s_ {y_i}) ^ {-2}\) ">2500.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.100 | \ (S_ {std}\) (unidades arbitrarias) ">12.36 | \ (s_ {std}\) ">0.02 | \ ((s_ {y_i}) ^ {-2}\) ">250,00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.200 | \ (S_ {std}\) (unidades arbitrarias) ">24.83 | \ (s_ {std}\) ">0.07 | \ ((s_ {y_i}) ^ {-2}\) ">204.08 | \ (w_i\) ">0.2313 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.300 | \ (S_ {std}\) (unidades arbitrarias) ">35.91 | \ (s_ {std}\) ">0.13 | \ ((s_ {y_i}) ^ {-2}\) ">59.17 | \ (w_i\) ">0.0671 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.400 | \ (S_ {std}\) (unidades arbitrarias) ">48.79 | \ (s_ {std}\) ">0.22 | \ ((s_ {y_i}) ^ {-2}\) ">20.66 | \ (w_i\) ">0.0234 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.500 | \ (S_ {std}\) (unidades arbitrarias) ">60.42 | \ (s_ {std}\) ">0.33 | \ ((s_ {y_i}) ^ {-2}\) ">9.18 | \ (w_i\) ">0.0104 |
Sumando los valores en la cuarta columna da
\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber \]
que utilizamos para calcular los pesos individuales en la última columna. Como comprobación de sus cálculos, la suma de los pesos individuales debe ser igual al número de estándares de calibración, n. La suma de las entradas en la última columna es de 6.0000, así que todo está bien. Después de calcular los pesos individuales, utilizamos una segunda tabla para ayudar en el cálculo de los cuatro términos de suma en las ecuaciones para la pendiente\(b_1\),, y la intersección y,\(b_0\).
| \(x_i\) | \(y_i\) | \(w_i\) | \(w_i x_i\) | \(w_i y_i\) | \(w_i x_i^2\) | \(w_i x_i y_i\) |
|---|---|---|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.0000 | \ (w_i y_i\) ">0.0000 | \ (w_i x_i^2\) ">0.0000 | \ (w_i x_i y_i\) ">0.0000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.2834 | \ (w_i y_i\) ">35.0270 | \ (w_i x_i^2\) ">0.0283 | \ (w_i x_i y_i\) ">3.5027 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (w_i\) ">0.2313 | \ (w_i x_i\) ">0.0463 | \ (w_i y_i\) ">5.7432 | \ (w_i x_i^2\) ">0.0093 | \ (w_i x_i y_i\) ">1.1486 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (w_i\) ">0.0671 | \ (w_i x_i\) ">0.0201 | \ (w_i y_i\) ">2.4096 | \ (w_i x_i^2\) ">0.0060 | \ (w_i x_i y_i\) ">0.7229 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (w_i\) ">0.0234 | \ (w_i x_i\) ">0.0094 | \ (w_i y_i\) ">1.1417 | \ (w_i x_i^2\) ">0.0037 | \ (w_i x_i y_i\) ">0.4567 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (w_i\) ">0.0104 | \ (w_i x_i\) ">0.0052 | \ (w_i y_i\) ">0.6284 | \ (w_i x_i^2\) ">0.0026 | \ (w_i x_i y_i\) ">0.3142 |
Sumando los valores en las últimas cuatro columnas da
\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber \]
lo que da la pendiente estimada y la intersección y estimada como
\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber \]
\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber \]
La ecuación de calibración es
\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber \]
La figura\(\PageIndex{31}\) muestra la curva de calibración para la regresión ponderada determinada aquí y la curva de calibración para la regresión no ponderada. Aunque las dos curvas de calibración son muy similares, existen ligeras diferencias en la pendiente y en la intersección y. Lo más notable es que la intersección y para la regresión lineal ponderada está más cerca del valor esperado de cero. Debido a que la desviación estándar para la señal, S std, es menor para concentraciones más pequeñas de analito, C std, una regresión lineal ponderada da más énfasis a estos estándares, permitiendo una mejor estimación de la y -interceptar.
Las ecuaciones para calcular los intervalos de confianza para la pendiente, la intersección y y la concentración de analito cuando se utiliza una regresión lineal ponderada no son tan fáciles de definir como para una regresión lineal no ponderada [Bonate, P. J. Anal. Chem. 1993, 65, 1367—1372]. El intervalo de confianza para la concentración del analito, sin embargo, está en su valor óptimo cuando la señal del analito está cerca del centroide ponderado, y c, de la curva de calibración.
\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber \]
Regresión lineal ponderada con errores en x e y
Si eliminamos nuestra suposición de que los errores indeterminados que afectan a una curva de calibración están presentes solo en la señal (y), entonces también debemos factorizar en el modelo de regresión los errores indeterminados que afectan la concentración del analito en los patrones de calibración (x). La solución para la línea de regresión resultante es computacionalmente más involucrada que la de las líneas de regresión no ponderadas o ponderadas. Aunque no consideraremos los detalles en este libro de texto, debe ser consciente de que descuidar la presencia de errores indeterminados en x puede sesgar los resultados de una regresión lineal.
Véase, por ejemplo, Comité de Métodos Analíticos, “Ajuste de una relación funcional lineal a datos con error en ambas variables”, Resumen Técnico AMC, marzo de 2002), así como Recursos Adicionales de este capítulo.
Regresión curvilínea, multivariable y multivariante
Un modelo de regresión lineal, a pesar de su aparente complejidad, es la relación funcional más simple entre dos variables. ¿Qué hacemos si nuestra curva de calibración es curvilínea, es decir, si es una línea curva en lugar de una línea recta? Un enfoque es intentar transformar los datos en una línea recta. De esta manera se han utilizado logaritmos, exponenciales, recíprocos, raíces cuadradas y funciones trigonométricas. Una gráfica de log (y) versus x es un ejemplo típico. Tales transformaciones no están exentas de complicaciones, de las cuales la más obvia es que los datos con una varianza uniforme en y no mantendrán esa varianza uniforme después de que se transforme.
Vale la pena señalar aquí que el término “lineal” no significa una línea recta. Una función lineal puede contener más de un término aditivo, pero cada término tiene uno y solo un parámetro multiplicativo ajustable. La función
\[y = ax + bx^2 \nonumber \]
es un ejemplo de una función lineal porque los términos x y x 2 incluyen cada uno un único parámetro multiplicativo, a y b, respectivamente. La función
\[y = x^b \nonumber \]
es no lineal porque b no es un parámetro multiplicativo; es, en cambio, una potencia. Es por esto que puedes usar regresión lineal para ajustar una ecuación polinómica a tus datos.
A veces es posible transformar una función no lineal en una función lineal. Por ejemplo, tomar el log de ambos lados de la función no lineal anterior da una función lineal.
\[\log(y) = b \log(x) \nonumber \]
Otro enfoque para desarrollar un modelo de regresión lineal es ajustar una ecuación polinómica a los datos, como\(y = a + b x + c x^2\). Puede usar regresión lineal para calcular los parámetros a, b y c, aunque las ecuaciones son diferentes a las de la regresión lineal de una línea recta. Si no puede ajustar sus datos usando una sola ecuación polinómica, es posible ajustar ecuaciones polinómicas separadas a segmentos cortos de la curva de calibración. El resultado es una curva de calibración continua única conocida como función spline. El uso de R para regresión curvilínea se incluye en el Capítulo 8.5.
Para obtener detalles sobre la regresión curvilínea, véase (a) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986; (b) Deming, S. N.; Morgan, S. L. Experimental Design: A Chemometric Approach, Elsevier: Amsterdam, 1987.
Los modelos de regresión de este capítulo se aplican únicamente a las funciones que contienen una sola variable dependiente y una sola variable independiente. Un ejemplo es la forma más simple de la ley de Beer en la que la absorbancia\(A\),, de una muestra a una sola longitud de onda\(\lambda\),, depende de la concentración de un solo analito,\(C_A\)
\[A_{\lambda} = \epsilon_{\lambda, A} b C_A \nonumber \]
donde\(\epsilon_{\lambda, A}\) es la absortividad molar del analito a la longitud de onda seleccionada y\(b\) es la longitud de trayectoria a través de la muestra. En presencia de un interferente\(I\), sin embargo, la señal puede depender de las concentraciones tanto del analito como del interferente
\[A_{\lambda} = \epsilon_{\lambda, A} b C_A + \epsilon_{\lambda, I} b C_I \nonumber \]
donde\(\epsilon_{\lambda, I}\) está la absortividad molar del interferente y C I es la concentración del interferente. Este es un ejemplo de regresión multivariable, que se trata con más detalle en el Capítulo 9 cuando consideramos la optimización de experimentos donde hay una sola variable dependiente y dos o más variables independientes.
En la regresión multivariada tenemos tanto múltiples variables dependientes, como la absorbancia de muestras a dos o más longitudes de onda, como múltiples variables independientes, como las concentraciones de dos o más analitos en las muestras. Como se discute en el Capítulo 0.2, podemos representar esto usando notación matricial
\[\begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & A & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{r \times c} = \begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & \epsilon b & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{r \times n} \times \begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & C & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{n \times c} \nonumber \]
donde hay\(r\) longitudes de onda,\(c\) muestras y\(n\) analitos. Cada columna de la\(\epsilon b\) matriz, por ejemplo, contiene el\(\epsilon b\) valor para un analito diferente en una de\(r\) las longitudes de onda, y cada fila en la\(C\) matriz es la concentración de uno de los\(n\) analitos en una de las\(c\) muestras. Consideraremos este enfoque con más detalle en el Capítulo 11.
Para una agradable discusión de la diferencia entre regresión multivariable y regresión multivariable, ver Hidalgo, B.; Goodman, M. “Regresión multivariable o multivariable”, Am. J. Salud Pública, 2013, 103, 39-40.