1.3: La simetría de los cristales

En el contexto de este capítulo, también se le invitará a visitar estas secciones...

• Elementos de simetría
• El teorema de restricción cristalográfica
• Representación de clases de cristal
• Representación de grupos Laue
• Representación de celosías Bravais

Acerca de la simetría en general

Muchas veces no nos damos cuenta, pero vivimos continuamente con simetría... La simetría es la consistencia, la repetición de algo en el espacio y/o en el tiempo, como se muestra en los ejemplos siguientes: un dibujo mural, los pétalos de flores, los dos lados de una mariposa, la sucesión de noche y día, una pieza musical, etc.

Simetría por repetición de patrones en un dibujo mural o en flores. El dibujo mural muestra la repetición por traducción. Las flores muestran repeticiones por rotaciones. La flor de la izquierda muestra repetición alrededor de un eje de rotación del orden 8 (8 pétalos idénticos alrededor del eje de rotación). La flor en el medio muestra un eje de rotación del orden 5 (dos familias diferentes de pétalos que se distribuyen alrededor del eje de rotación). Además, cada pétalo en ambas flores muestra un plano de simetría que lo divide en dos partes idénticas (aproximadamente), lo mismo que ocurre con la mariposa que se muestra a la derecha. Si al lector le sorprende el hecho de que digamos que las dos partes separadas por un plano de simetría (espejo) son sólo “aproximadamente” idénticas, es porque realmente no son idénticas; no pueden superponerse, pero este es un tema que se explicará en otra sección.

Simetría repitiendo eventos: Día - Noche - Día

Simetría en la música. Un fragmento de “Seis melodías unisono” de Bartók.

(El diagrama en la parte inferior representa la simetrización del que se muestra arriba)

La palabra “Simetría”, cuidadosamente escrita con letras algo distorsionadas, muestra un eje doble (una rotación de 180 grados) perpendicular a la pantalla.

La siguiente oración sirve también para ilustrar el concepto de simetría:

UN HOMBRE, UN PLAN, UN CANAL: PANAMA

donde, si olvidamos las comas y el colon, se convierte en:

AMANAPLANANANALPANAMA

que se puede leer de derecha a izquierda con exactamente el mismo significado que el anterior. Se trata de un caso similar a los números “palindrómicos” (232 o 679976).

Son muchos los vínculos en los que el lector puede encontrar información sobre el concepto de simetría y hemos seleccionado algunos de ellos: simetría y forma del espacio, algunos otros en el contexto de conceptos cristalográficos, algunos con elementos decorativos patrones, o en el contexto de los minerales. Incluso existe una sociedad internacional para el estudio de la simetría.

Los conocimientos esenciales sobre la morfología cristalina, los elementos de simetría y su combinación para generar objetos repetitivos en el espacio, estuvieron bien establecidos entre los siglos XVII y XIX, como se afirma en otras partes de estas páginas...

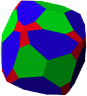
Específicamente, en los objetos finitos, hay una serie de operaciones (elementos de simetría) que describen repeticiones. En el dibujo mural (mostrado arriba) encontramos operaciones de traslación (el motivo se repite por traducción). La repetición de los pétalos en las flores nos muestran operaciones rotacionales (el motivo se repite por rotación) alrededor de un eje de simetría (o eje de rotación). Y, aunque no exactamente, la simetría mostrada en la frase o en el fragmento musical (mostrado arriba), nos llevan a considerar otras operaciones de simetría conocidas como planos de simetría (planos de reflexión, o planos espejo); la misma operación que ocurre cuando te miras a un espejo. De igual manera, por ejemplo, si observamos la relación entre los objetos tridimensionales en algunas de las imágenes que se muestran a continuación, descubriremos un nuevo elemento de simetría llamado centro de simetría (o centro de inversión), que es un punto imaginario entre objetos (o dentro del objeto) como se muestra en algunos dibujos a continuación.

En términos generales, y teniendo en cuenta que las operaciones traslacionales puras no se consideran estrictamente como operaciones de simetría, podemos decir que los objetos finitos pueden contenerse a sí mismos, o pueden ser repetidos (excluyendo la traducción) por los siguientes elementos de simetría:

• La operación de identidad es el elemento de simetría más simple de todos — ¡no hace nada! Pero es importante porque todos los objetos por lo menos tienen el elemento de identidad, y hay muchos objetos que no tienen otros elementos de simetría.

• El reflejo es la operación de simetría que se produce cuando ponemos un objeto frente a un espejo. La imagen se encuentra perpendicular al plano de reflexión y equidistante de ese plano, en el lado opuesto del plano. El objeto resultante puede ser distinguible o indistinguible del original, normalmente distinguible, ya que no pueden superponerse. Si el objeto resultante es indistinguible del original, es porque el plano de reflexión está pasando por el objeto.

• La operación de inversión ocurre a través de un solo punto llamado centro de inversión. Cada parte del objeto se mueve a lo largo de una línea recta a través del centro de inversión hasta un punto a la misma distancia del centro de inversión. El objeto resultante puede ser distinguible o indistinguible del original, normalmente distinguible, ya que no pueden superponerse. Si el objeto resultante es indistinguible del original, es porque el centro de inversión está dentro del objeto.

• Las operaciones de rotación (tanto propias como incorrectas) ocurren con respecto a una línea llamada eje de rotación. a) Se realiza una rotación adecuada girando el objeto 360°/ n, donde n es el orden del eje. El objeto girado resultante siempre es indistinguible del original. b) Se realiza una rotación inadecuada rotando el objeto 360°/ n seguido de una reflexión a través de un plano perpendicular al eje de rotación. El objeto resultante puede ser distinguible o indistinguible del original, normalmente distinguible, ya que no pueden superponerse. Si el objeto resultante es indistinguible del original, es porque el eje de rotación incorrecto está pasando por el objeto.

Además del nombre de los elementos de simetría, utilizamos símbolos gráficos y numéricos para representarlos. Por ejemplo, un eje de rotación de orden 2 (un eje binario) está representado por el número 2, y un plano de reflexión se representa con la letra m.

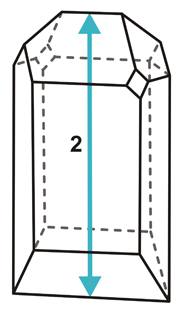
Izquierda: Poliedro que muestra un eje de rotación doble (2) que pasa por los centros de los bordes superior e inferior

Derecha: Poliedro que muestra un plano de reflexión (m) que relaciona (como lo hace un espejo) la parte superior con la parte inferior

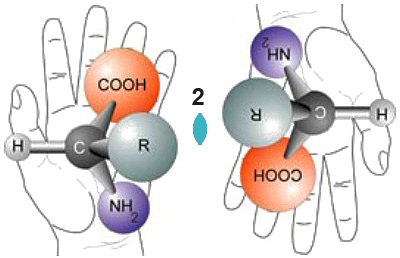
Manos y modelos moleculares relacionados por un eje doble (2) perpendicular al plano de dibujo

Manos y modelos moleculares relacionados a través de un plano espejo (m) perpendicular al plano de dibujo

Manos (izquierda y derecha) relacionadas a través de un centro de simetría

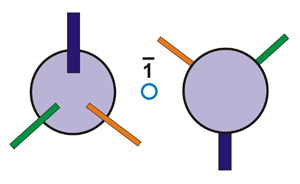
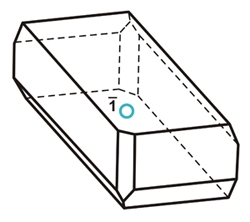
Dos objetos relacionados por un centro de simetría y un poliedro que muestran un centro de simetría en su centro

La asociación de elementos de rotación con centros o planos de simetría genera nuevos elementos de simetría llamados rotaciones impropias.

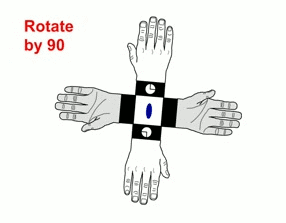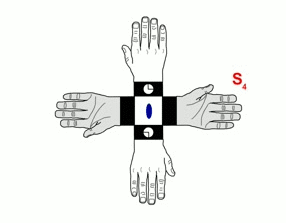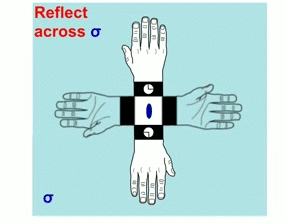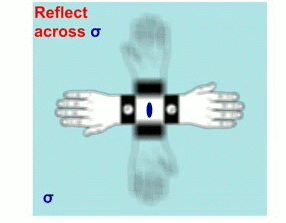
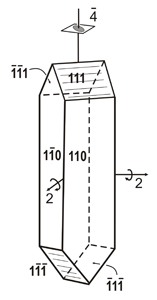
Izquierda: Un eje impropio cuádruple implica rotaciones de 90º seguidas de reflexión a través de un plano espejo perpendicular al eje. (Animación tomada de M. Kastner, T. Medlock & K. Brown, Univ. de Bucknell)

Derecha: Eje de rotación inadecuada, mostrado verticalmente, en un cristal de urea. El significado de los tripletes numéricos mostrados se discutirá en otro capítulo.

Combinando los ejes de rotación y los planos especulares con las traslaciones características de los cristales (que se muestran a continuación), aparecen nuevos elementos de simetría, con algunos componentes “deslizantes”: ejes de tornillo (o ejes helicoidal) y Planos de Planeo.

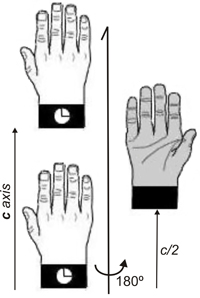
Eje de tornillo doble. Un eje de tornillo consiste en una rotación seguida de una traslación

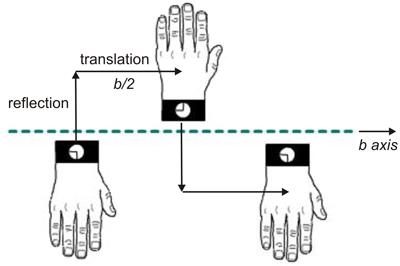
Plano de deslizamiento. Un plano de deslizamiento consiste en una reflexión seguida de una traslación

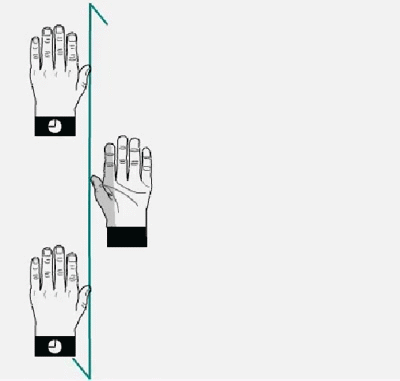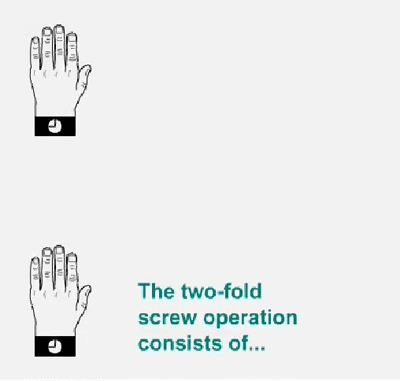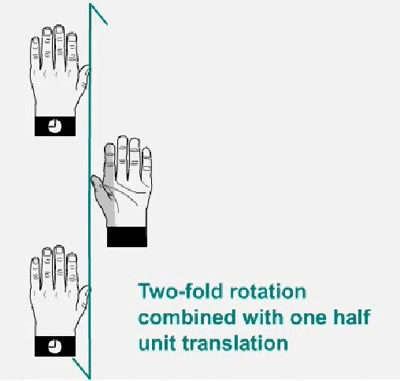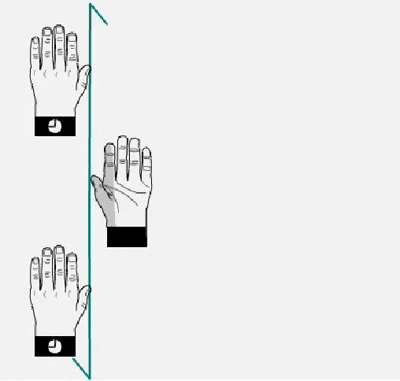
Eje de tornillo doble aplicado a una mano izquierda. La mano gira 180º y mueve la mitad de la traslación de celosía en la dirección del eje del tornillo, y así sucesivamente. Tenga en cuenta que la mano siempre permanece como mano izquierda.

(Animación tomada de M. Kastner, T. Medlock & K. Brown, Univ. de Bucknell)

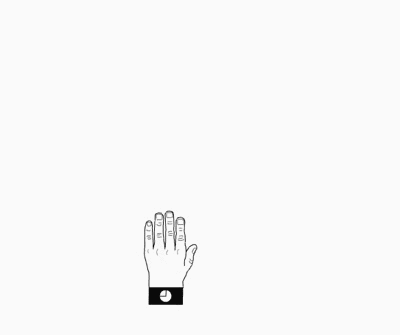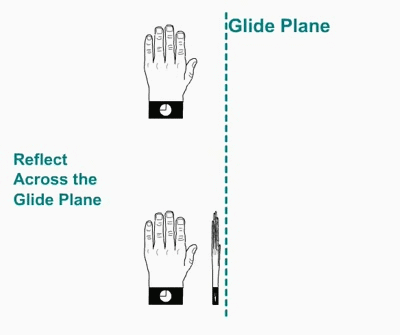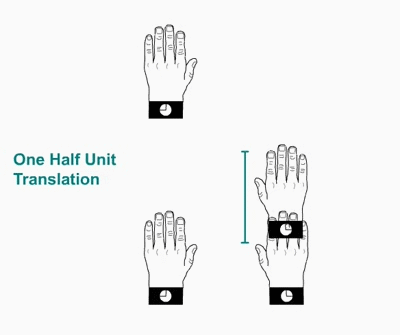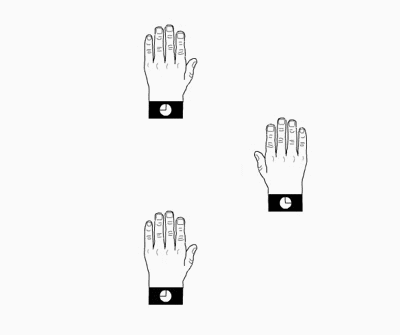
Planeo plano.aplicado a una mano izquierda. La mano izquierda se refleja en el plano, generando una mano derecha que mueve la mitad de la traslación de celosía en la dirección de la operación de planeo.

(Animación tomada de M. Kastner, T. Medlock & K. Brown, Univ. de Bucknell)

Los elementos de simetría de tipos centro o plano espejo relacionan objetos de una manera peculiar; de la misma manera que nuestras dos manos están relacionadas una con la otra: no son superponibles. Los objetos que en sí mismos no contienen ninguno de estos elementos de simetría (centro o plano) se denominan quirales y su repetición a través de estos elementos (centro o plano) producen objetos que se denominan enantiómeros con respeto a los originales. La imagen especular de una de nuestras manos es el enantiómero del que ponemos frente al espejo. En cuanto a la quiralidad de los cristales y de sus unidades constructivas (moleculares o no), los lectores avanzados también deben consultar el artículo de Howard D. Flack que se encuentra a través de este enlace.

La imagen especular de cualquiera de nuestras manos es el enantiómero de la otra mano. Son objetos no superponibles y como no contienen (en sí mismos) centros de simetría o planos de simetría, se denominan objetos quirales.

Las moléculas quirales tienen propiedades diferentes a sus enantiómeros y por eso es importante que seamos capaces de diferenciarlas. La correcta determinación de la configuración absoluta o estructura absoluta de una molécula (diferenciación entre enantiómeros) se puede hacer de manera segura solo a través de difracción de rayos X, pero esto se explicará en otro capítulo

Así, cualquier objeto finito (como un cristal de cuarzo, una silla o una flor) muestra que ciertas partes del mismo se repiten mediante operaciones de simetría que atraviesan un punto del objeto. Este conjunto de operaciones de simetría se conoce como grupo de puntos de simetría. El lector avanzado también tiene la oportunidad de visitar el agradable trabajo sobre elementos de simetría de grupos puntuales que se ofrecen a través de estos enlaces:

• Dean H. Johnston de la Universidad Otterbein, y
• Margaret Kastner, Timathy Medlock y Kristy Brown de la Universidad de Bucknell.

Un buen sitio web general sobre simetría en cristalografía es ofrecido por el Departamento de Química y Bioquímica de la Universidad de Oklahoma.

Adicionalmente, el lector puede descargar (totalmente libre de virus!!!) y ejecutar en su propio ordenador esta aplicación Java que, como introducción a la simetría de los poliedros, que fue desarrollada por Gervais Chapuis y Nicolas Schöni (École Polytechnique Fédérale de Lausanne, Suiza).

Simetría en cristales

En los cristales, los ejes de simetría (ejes de rotación) solo pueden ser de dos veces (2), tres veces (3), cuatro veces (4) o seis- fold (6), dependiendo del número de veces (orden de rotación) que un motivo pueda repetirse mediante una operación de rotación, transformándose en un nuevo estado indistinguible de su estado inicial. Así, un eje de rotación de orden 3 (3 veces) produce 3 repeticiones (copias) del motivo, una cada 120 grados (= 360/ 3) de rotación. Si el lector se pregunta por qué solo los ejes de simetría de orden 2, 3, 4 y 6 pueden ocurrir en los cristales, y no 5 -, 7 -fold, etc., recomendamos las explicaciones dadas en otra sección.

Las rotaciones inadecuadas (rotaciones seguidas de reflexión a través de un plano perpendicular al eje de rotación) se designan por el orden de rotación, con una barra por encima de ese número.

Los ejes de tornillo (o ejes helicoidales, es decir, ejes de simetría que implican rotación seguida de una traslación a lo largo del eje) están representados por el orden de rotación, con un subíndice agregado que cuantifica la traslación a lo largo del eje. Así, un eje de tornillo de tipo 6 ₂ significa que en cada una de las seis rotaciones se produce una traslación asociada de 2/6 del eje de la celda elemental en esa dirección.

Los planos espejo están representados por la letra m.

Los planos de planeo (planos especulares que implican reflexión y una traslación paralela al plano) están representados por las letras a, b, c, n o d, dependiendo de si la traslación asociada con el la reflexión es paralela a las traslaciones reticulares (a, b, c), paralela a la diagonal de un plano reticular (n), o paralela a una diagonal de la celda unitaria (d).

Las letras y números que se utilizan para representar los elementos de simetría también tienen una equivalencia con algunos símbolos gráficos.

Pero para seguir hablando de simetría en cristales, es necesario introducir y recordar el aspecto fundamental que define a los cristales, que es la repetición periódica por traducción de motivos (átomos, moléculas o iones). Esta repetición, que se ilustra en dos dimensiones con círculos grises en la figura de abajo, se deriva del concepto matemático de celosía que veremos más adecuadamente en otro capítulo.

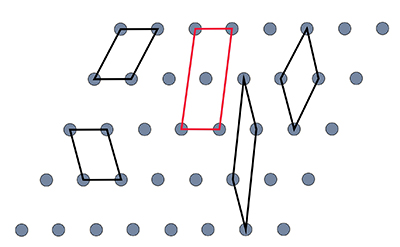
En un conjunto periódico y repetitivo de motivos (círculos grises en la figura bidimensional anterior) se pueden encontrar infinitas unidades básicas (celdas unitarias) muy diferentes en apariencia y especificación, cuya repetición genera la misma celosía matemática. Tenga en cuenta que todas las celdas unitarias representadas delimitadas por líneas negras contienen en total un solo círculo dentro de ellas, ya que cada vértice contiene una cierta fracción de un círculo dentro de la celda. A estas se les llama células primitivas. Sin embargo, la celda delimitada por líneas rojas contiene un total de dos círculos grises en su interior (uno correspondiente a los vértices y otro completo en el centro). Este tipo de celda unitaria se llama genéricamente no primitiva.

La repetición periódica, característica de la estructura interna de los cristales, está representada por un conjunto de traslaciones en las tres direcciones del espacio, de manera que los cristales pueden verse como el apilamiento del mismo bloque en tres dimensiones. Cada bloque, de cierta forma y tamaño (pero siendo todos idénticos), se denomina celda unitaria o celda elemental. Su tamaño está determinado por la longitud de sus tres bordes (a, b, c) y los ángulos entre ellos (alfa, beta, gamma: α, β, γ).

Apilamiento de celdas unitarias que forman un cristal octaédrico y parámetros que caracterizan la forma y el tamaño de una celda elemental (o celda unitaria)

Como se mencionó anteriormente, todos los elementos de simetría que pasan por un punto de un objeto finito, definen la simetría total del objeto, lo que se conoce como la simetría de grupo de puntos del objeto. Obiosamente, los elementos de simetría que implican cualquier traslación de celosía (planos de deslizamiento y ejes de tornillo), no son operaciones de grupo de puntos.

Existen muchos grupos de puntos de simetría, pero en los cristales deben ser consistentes con la periodicidad cristalina (periodicidad de traducción). Así, en los cristales, solo son posibles rotaciones (ejes de simetría) de orden 2, 3, 4 y 6, es decir, solo se permiten rotaciones de 180º (= 360/2), 120º (= 360/3), 90º (= 360/4) y 60º (= 360/6). Véase también el teorema de restricción cristalográfica. Por lo tanto, sólo se permiten 32 grupos puntuales en el estado cristalino de la materia. Estos grupos de 32 puntos también se conocen en Cristalografía como las 32 clases de cristal.

grupo de puntos. periodicidad traslacional de cristal = 32 clases de cristal

Representación gráfica de las 32 clases de cristal

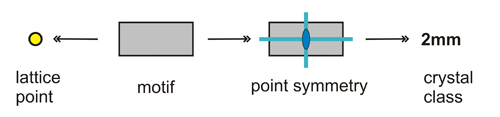
El motivo, representado por un solo ladrillo, también puede ser representado por un punto de celosía. Muestra la simetría puntual 2mm

En las tres tablas siguientes se muestran dibujos animados sobre las 32 clases de cristal, agrupadas en términos del llamado sistema cristalino (columna izquierda), un modo de clasificación en términos de simetría mínima, como se muestra a continuación.

	Los enlaces a continuación ilustran las 32 clases de cristales usando algunas morfologías cristalinas Estos dibujos animados interactivos necesitan el entorno Java y por lo tanto no se ejecutarán con todos los navegadores
Triclínica	1	1
monoclínico	2	m	2/m
Ortorrómbico	222	mm2	mmm
Tetragonal	4	4	4/m	422	4mm	42m	4/mmm
Cúbico	23	m3	432	43m	m3m
Trigonal	3	3	32	3m	3m
Hexagonal	6	6	6/m	622	6mm	6m2	6/mmm

	Los enlaces a continuación ilustran las 32 clases de cristales usando algunas morfologías cristalinas Se trata de gifs animados no interactivos obtenidos de las animaciones Java que aparecen en http://webmineral.com. Se ejecutarán con todos los navegadores
Triclínica	1	1
monoclínico	2	m	2/m
Ortorrómbico	222	mm2	mmm
Tetragonal	4	4	4/m	422	4mm	42m	4/mmm
Cúbico	23	m3	432	43m	m3m
Trigonal	3	3	32	3m	3m
Hexagonal	6	6	6/m	622	6mm	6m2	6/mmm

	Los enlaces a continuación muestran pantallas animadas de los elementos de simetría en cada una de las 32 clases de cristal: (tomado de Marc De Graef)
Triclínica	1	1
monoclínico	2	m	2/m
Ortorrómbico	222	mm2	mmm
Tetragonal	4	4	4/m	422	4mm	42m	4/mmm
Cúbico	23	m3	432	43m	m3m
Trigonal	3	3	32	3m	3m
Hexagonal	6	6	6/m	622	6mm	6m2	6/mmm

Lluis Casas y Eugenia Estop, del Departamento de Geología de la Universidad de Barcelona, ofrecen 32 archivos pdf que, de manera interactiva, permiten jugar muy fácilmente con los grupos de 32 puntos a través de la simetría de los sólidos cristalinos.

Adicionalmente, el lector puede descargar y ejecutar en su propio ordenador esta aplicación Java que, como introducción a la simetría de los poliedros, fue desarrollada por Gervais Chapuis y Nicolas Schöni (École Polytechnique Fédérale de Lausanne, Suiza).

Alternativamente, el lector interesado puede ver interactivamente algunos poliedros típicos de los 7 sistemas cristalinos, a través del Instituto Gemológico Español.

De las 32 clases de cristal, solo 11 contienen el centro de simetría del operador, y estas 11 clases de cristales centrosimétricos se conocen como grupos Laue.

clase cristal. centro de simetría = 11 grupos Laue

Representación gráfica de los 11 grupos Laue (clases de cristales centrosimétricos)

Además, los modos de repetición por traducción en cristales deben ser compatibles con los posibles grupos de puntos (las 32 clases de cristal), y es por ello que encontramos solo 14 tipos de celosías traslacionales que son compatibles con las clases de cristal. Este tipo de celosías (modos de repetición traslacional) se conocen como las celosías de Bravais (puedes verlas aquí). La simetría traslacional de una distribución ordenada de objetos tridimensionales puede ser descrita por muchos tipos de celosías, pero siempre hay una de ellas más adecuada al objeto, es decir: la que mejor describe la simetría del objeto. Como las propias celosías tienen su propia distribución de elementos de simetría, debemos ajustarlas a los elementos de simetría de la estructura.

periodicidad traslacional de cristal. 32 clases de cristal = 14 celosías Bravais

Representación gráfica de las 14 celosías Bravais

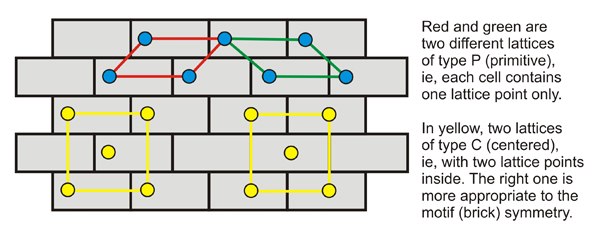
Una pared de ladrillo se puede estructurar con muchos tipos diferentes de celosías, con diferentes orígenes, y definiendo puntos reticulares que representan el ladrillo. Pero hay una celosía que es más apropiada a la simetría del ladrillo y a la forma en que los ladrillos construyen la pared.

La adecuación de una celosía a la estructura se ilustra en los ejemplos bidimensionales que se muestran a continuación. En los tres casos se muestran dos celosías diferentes, una oblicua y primitiva y otra rectangular y centrada. En los dos primeros casos, las celosías rectangulares son las más adecuadas. Sin embargo, la deformación de la estructura en el tercer ejemplo conduce a relaciones métricas que hacen que esa sea la celosía más apropiada, la primitiva oblicua, hexagonal en este caso.

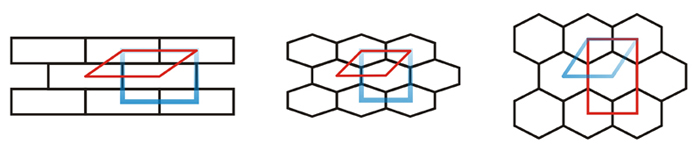
Adecuación del tipo de celosía a la estructura. La celosía azul es la mejor en cada caso.

Finalmente, combinando las 32 clases de cristal (grupos de puntos cristalográficos) con las 14 celosías de Bravais, encontramos hasta 230 formas diferentes de replicar un objeto finito (motivo) en el espacio tridimensional. Estas 230 formas de repetir patrones en el espacio, que son compatibles con las 32 clases de cristal y con las 14 celosías de Bravais, se denominan grupos espaciales, y representan las 230 formas diferentes de ajustar las celosías Bravais a la simetría de los objetos. El lector interesado también deberá consultar el excelente trabajo sobre los elementos de simetría presentes en los grupos espaciales, ofrecidos por Margaret Kastner, Timathy Medlock y Kristy Brown a través de este enlace de la Universidad Bucknell.

32 clases de cristal + 14 celosías Bravais = 230 Grupos espaciales

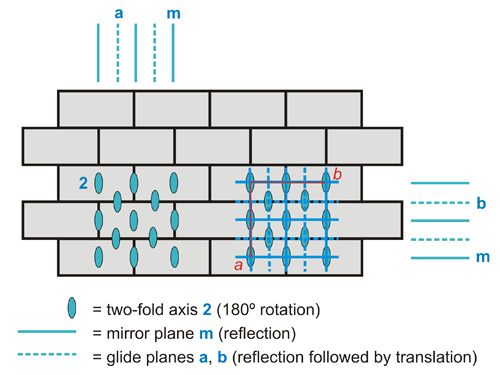
Una pared de ladrillos que muestra la celosía más adecuada que mejor representa tanto el ladrillo como su simetría. Obsérvese que en este caso la simetría puntual del ladrillo y la simetría puntual del punto reticular son coincidentes. El grupo espacial, considerando el grosor del ladrillo, es Cmm2.

Las 32 clases de cristal, las 14 celosías Bravais y los 230 grupos espaciales se pueden clasificar, según su simetría mínima alojada, en 7 sistemas cristalinos. La simetría mínima produce algunas restricciones en los valores métricos (distancias y ángulos) que describen la forma y el tamaño de la celosía.

32 clases, 14 celosías, 230 grupos espaciales/simetría cristalina = 7 sistemas cristalinos

Todo esto se resume en la siguiente tabla:

Clases de cristal (* Laue)	Celosías de cristal compatibles y su simetría	Número de grupos espaciales	Simetría mínima	Restricciones métricas	Sistema de cristal
1 1 *	P 1	2	1 o 1	ninguno	Triclínica
2 m 2/m *	P C (I) 2/m	13	Uno 2 o 2	α=γ=90	Monocínicos
222 2mm mmm *	P C (A, B) I F mmm	59	Tres 2 o 2	α=β=γ=90	Ortorrómbico
4 4 4/m * 422 4mm 42m 4/mmm *	P I 4/mmm	68	Uno 4 o 4	a=b α=β=γ=90	Tetragonal
3 3 * 32 3m 3m *	P (R) 3m 6/mmm	25	Uno 3 o 3	a=b=c α=β=γ (o Hexagonal)	Trigonal
6 6 6m * 622 6mm 6m2 6/mmm *	P 6/mmm	27	Uno 6 o 6	a=b α=β=90 γ=120	Hexagonal
23 m3 * 432 43m m3m *	P I F m3m	36	Cuatro 3 o 3	a=b=c α=β=γ=90	Cúbico
Total: 32, 11 *	14 independientes	230			7

Los 230 grupos de espacio cristalográfico se enumeran y describen en las Tablas Internacionales para Cristalografía de Rayos X, donde se clasifican según grupos puntuales y sistemas cristalinos. Los compuestos quirales que se preparan como un solo enantiómero (por ejemplo, moléculas biológicas) pueden cristalizar en solo un subconjunto de 65 grupos espaciales, aquellos que no tienen operaciones de simetría espejo y/o inversión.

A continuación se muestra una composición de parte de la información contenida en estas tablas, correspondiente al grupo de espacios Cmm2, donde C significa que la estructura se describe en términos de una celosía centrada en las caras separadas por el eje c. La primera m representa un plano espejo perpendicular al eje a. El segundo m significa otro plano espejo (en este caso perpendicular a la segunda dirección cristalográfica principal), el eje b. El número 2 se refiere al doble eje paralelo a la tercera dirección cristalográfica, el eje c.

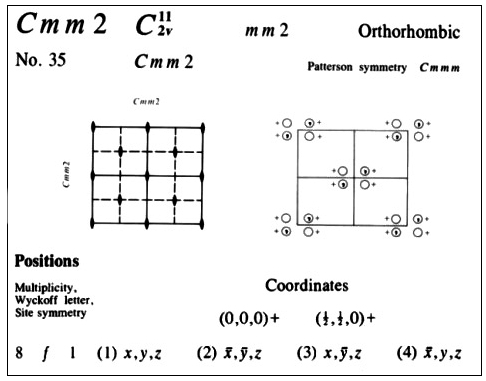
Resumen de la información mostrada en las Tablas Internacionales de Cristalografía de Rayos X para el grupo espacial Cmm2

Y este es otro ejemplo para el grupo espacial P21/c, centrosimétrico y basado en una primitiva celosía monoclínica, como aparece en las Tablas Internacionales para Cristalografía de Rayos X

Resumen de la información mostrada en las Tablas Internacionales de Cristalografía de Rayos X para el grupo espacial P2 ₁ /c

El lector avanzado también puede consultar:

• el paquete de enseñanza y aprendizaje ofrecido por la Universidad de Cambridge sobre ideas y principios fundamentales asociados al campo de la cristalografía
• el libro de hipertexto "Diagramas y tablas de grupos de espacios cristalográficos”
• el artículo de Dauter & Jaskolski titulado Cómo leer y entender el Volumen A de Tablas Internacionales para Cristalografía
• el servidor cristalográfico Bilbao, que es una excelente herramienta para el manejo de la simetría en cristalografía, y/o
• el llamado decodificador de grupos espaciales ofrecido por Bernhard Rupp.

¡Los cristógrafos nunca se aburren! Intenta disfrutar de la belleza, buscando la simetría de los objetos que te rodean, y particularmente en los objetos que se muestran a continuación...

Busque posibles celdas unitarias y elementos de simetría en estas estructuras hechas con ladrillos

(la solución se obtiene haciendo clic en la imagen)

Hay una pregunta que seguramente los lectores habrán considerado... En este capítulo hemos mostrado elementos de simetría que operan dentro de los cristales, pero aún no hemos dicho cómo podemos averiguar la existencia de tales operaciones, cuando de hecho, y en el mejor de los casos, ¡sólo podríamos visualizar el hábito externo de los cristales si están bien formados! Si bien aquí no vamos a responder a esta pregunta, podemos anticipar que esta respuesta vendrá dada por el comportamiento de los cristales cuando los iluminemos con esa luz especial que conocemos como rayos X, pero ésta será objeto de otro capítulo.

En cualquier caso, ¡no termina aquí! Hay muchas más cosas de las que hablar. Vamos.