1.4: Celosías directas y recíprocas
- Page ID
- 77868
Empecemos con un resumen de varios conceptos vistos en capítulos anteriores...
Cualquier distribución repetitiva y periódica de un conjunto de objetos (o motivos) puede caracterizarse, o describirse, por traducciones que repiten periódicamente el conjunto de objetos. Las traducciones implícitas generan lo que llamamos una celosía directa (o celosía real).


Izquierda: Fragmento de una distribución de un conjunto de objetos que producen una celosía directa en 2 dimensiones. Como ejemplo, uno de los conjuntos infinitos de motivos (pequeños mosaicos) que producen la distribución repetitiva y periódica se muestra dentro de los cuadrados amarillos. Las dimensiones del cuadrado amarillo representan las traducciones de la celosía directa
Derecha: Fragmento de un mosaico en La Alhambra que muestra un patrón periódico bidimensional. Estas traducciones periódicas se pueden descubrir en el mosaico y producir una celosía directa bidimensional. El cuadrado rojo representa las traducciones de la celosía directa más pequeña producida por las distribuciones periódicas de las pequeñas piezas de este mosaico.El cuadrado amarillo representa otra celosía posible, una más grande, no primitiva.
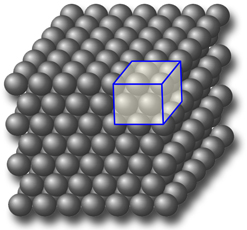
Apilamiento periódico de bolas, produciendo una red tridimensional (celosía directa). El motivo que se repite en las tres direcciones del espacio es el contenido de la pequeña caja con bordes azules, la llamada “celda unitaria”.
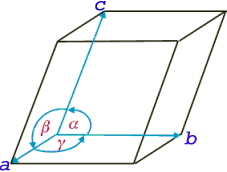
Las traducciones que describen la periodicidad en cristales pueden expresarse como una combinación lineal de tres traducciones básicas, no coplanarias, es decir independientes, conocidas como ejes reticulares o reticulares (o ejes de celdas unitarias). Estos ejes definen un paralelogramo (en 2 dimensiones), o un paralelepípedo (en 3 dimensiones) conocido como celda unitaria (o celda elemental). Esta área elemental (en casos bidimensionales), o volumen elemental (en casos tridimensionales), que contiene el conjunto mínimo de la distribución periódica, genera (por traducciones) la distribución completa que, en nuestro caso tridimensional atómico, llamamos cristal.
Además de que la celda unitaria es la unidad repetitiva más pequeña en lo que respecta a las traducciones, el lector debe tener en cuenta que el sistema de ejes que define la celda unitaria realmente define el sistema de referencia para describir las coordenadas posicionales de cada átomo dentro de la célula.
Izquierda: Celda elemental (o celda unitaria) definida por las 3 traslaciones reticulares no coplanares (ejes de celda o ejes de celosía)
Derecha: Formación de cristales apilando muchas celdas unitarias en 3 direcciones espaciales
En general, dentro de la celda unitaria hay un conjunto mínimo de átomos (iones o moléculas) que se repiten dentro de la célula debido a los elementos de simetría de la estructura cristalina. Este conjunto mínimo de átomos (iones o moléculas) que generan todo el contenido de la celda unitaria (después de aplicarles los elementos de simetría) se conoce como la unidad asimétrica.


El motivo estructural mostrado en la figura izquierda se repite mediante un elemento de simetría (operación de simetría), en este caso un eje de tornillo
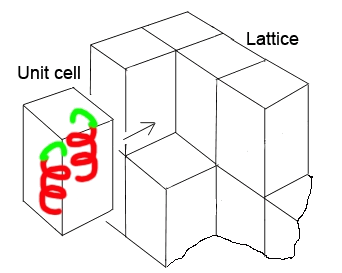
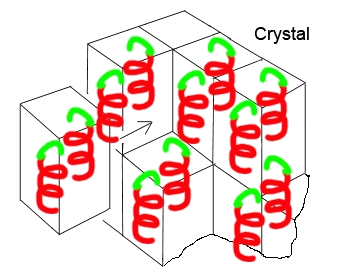
La repetición del motivo (unidad asimétrica) genera el contenido completo de la celda unitaria, y la repetición de celdas unitarias genera todo el cristal
La celosía, que es un concepto matemático puro, se puede seleccionar de diversas maneras en una misma distribución periódica real. Sin embargo, sólo una de estas celosías “encaja” mejor con la simetría de la distribución periódica de los motivos...

Distribución periódica bidimensional de un motivo que contiene dos objetos (un triángulo y un círculo)
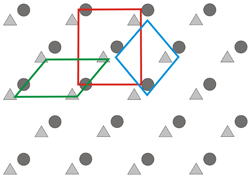
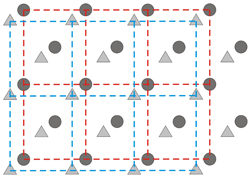
Izquierda: Celdas unitarias correspondientes a posibles celosías directas (=celosías reales) que pueden ser dibujadas sobre la distribución periódica mostrada arriba. Solo una de las celdas unitarias (la roja) es más apropiada porque encaja mucho mejor con la simetría de la distribución
Derecha: El glóbulo rojo de la figura izquierda (una celosía centrada) encaja mejor con la simetría de la distribución, y puede descomponerse en dos celosías idénticas, una por cada objeto del motivo.
Como se muestra en las figuras anteriores, aunque especialmente en la derecha, cualquier celosía que describa la repetición del motivo (triángulo + círculo) puede descomponerse en dos celosías equivalentes idénticas (una por cada objeto del motivo). Así, el concepto de celosía es independiente de la complejidad del motivo, de manera que solo podemos utilizar una celosía, ya que representa todas las equivalentes restantes. Una vez que hemos elegido una celosía representativa, apropiada a la simetría de la estructura, cualquier punto reticular (o nodo reticular) puede ser descrito por un vector que es una combinación lineal (con números enteros) del directo ejes reticulares: R = m a + n b + p c, donde m, n y p son enteros. Los puntos no reticulares se pueden alcanzar usando el vector R más cercano, y agregándole las fracciones correspondientes de los ejes reticulares para alcanzarlo:
r = R + r' = (m a + n b + p c) + (x a + y b + z c)
Vector de posición para cualquier punto no reticular de una red directa
donde x, y, z representan las fracciones adimensionales correspondientes de los ejes X/a, Y/b, Z/c y X, Y, Z las longitudes correspondientes.
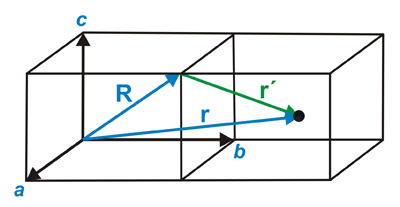
Vector de posición para un punto no reticular (círculo negro)
El lector también debería echar un vistazo a los capítulos sobre celosías y celdas unitarias que ofrece la Universidad de Cambridge.
Alternativamente, el lector puede descargar y ejecutar en su propio ordenador esta aplicación Java que ilustra el concepto de celosía (está totalmente libre de virus y fue desarrollada por Gervais Chapuis y Nicolas Schöni, École Polytechnique Fédérale de Lausanne, Suiza).
Veamos ahora algunos conceptos nuevos sobre celosías directas (= celosías reales)...
Desde un punto de vista geométrico, sobre una celosía podemos considerar algunas líneas reticulares y planos reticulares que son los que pasan por los puntos reticulares (o nodos reticulares). Así como hicimos con las celosías (eligiendo una de ellas de todas las equivalentes), hacemos lo mismo con las líneas y planos reticulares. Una línea reticular o un plano reticular se puede utilizar como representante de toda la familia de líneas paralelas o planos paralelos.
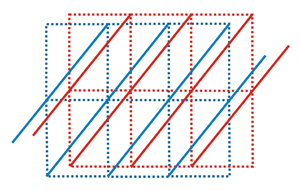
Siguiendo con el argumento dado anteriormente, cada motivo en una distribución repetitiva genera su propia celosía, aunque todas estas celosías son idénticas (rojo y azul). De las dos familias de celosías equivalentes mostradas (rojo y azul) podemos elegir sólo una de ellas, en el entendimiento de que también representa las restantes equivalentes. Tenga en cuenta que la distancia entre los planos dibujados en cada celosía (espaciado interplanar) es la misma para las familias azules o rojas. Sin embargo, la familia de planos rojos está separada de la familia de planos azules por una distancia que depende de la separación entre los objetos que produjeron la celosía. Esta distancia entre los planos de diferentes familias se puede llamar la distancia geométrica fuera de fase.
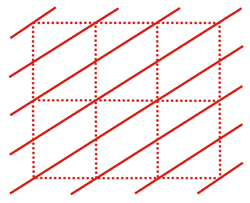
Izquierda: Familia de planos reticulares cortando el eje vertical de la celda en 2 partes y el eje horizontal en 1 parte. Estos planos son paralelos al tercer eje reticular (no mostrado en la figura).
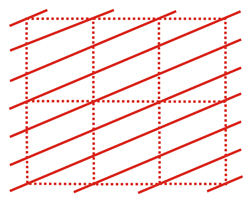
Derecha: Familia de planos reticulares cortando el eje vertical de la celda en 3 partes y el eje horizontal en 1 parte. Estos planos son paralelos al tercer eje reticular (no mostrado en la figura).

El número de piezas en las que una familia de planos corta los ejes de las celdas se puede asociar con un triplete de números que identifican esa familia de planos. En las tres figuras anteriores, el número de cortes, y por lo tanto los tripletes numéricos serían (110), (210) y (310), respectivamente, según los ejes vertical, horizontal y perpendicular a la figura. En esta figura, los tripletes numéricos para los planos dibujados son (022), es decir, la familia de planos no corta el eje a, sino que corta los ejes b y c en 2 partes idénticas, respectivamente.
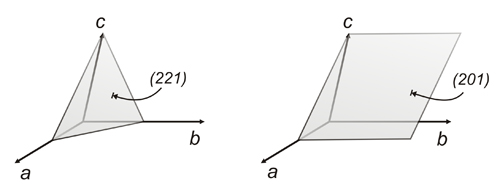
El plano dibujado en el lado izquierdo de la figura anterior corta el eje a en 2 partes iguales, el eje b en 2 partes y el eje c en 1 parte. De ahí que el triplete numérico que identifique el plano será (221). El plano dibujado en el lado derecho de la figura corta el eje a en 2 partes, es paralelo al eje b y corta el eje c en 1 parte. Por lo tanto, el triplete numérico será (201).
Un plano único, como el dibujado en la figura superior derecha, definido por el triplete numérico conocido como índices de Miller, representa y describe toda la familia de planos paralelos que pasan por cada elemento del motivo. Así, en una estructura cristalina, habrá tantas familias de planos como sea posible que existan trillizos numéricos con la condición de que estos números sean primos, uno al otro (no teniendo un divisor común).
Los índices Miller están representados genéricamente por el triplete de letras hkl. Si hay divisores comunes entre los índices de Miller, el triplete numérico representaría solo una sola familia de planos. Por ejemplo, la familia con índices (330), que no son estrictamente reticulares, puede considerarse como la representativa de 3 familias de índices (110) con una distancia geométrica fuera de fase (entre las familias) de 1/3 del original (ver las cifras a continuación).
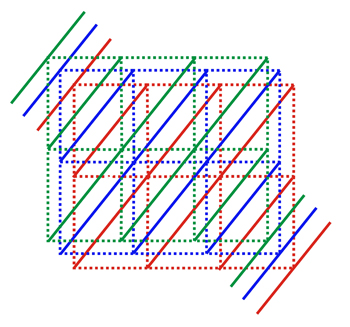
Izquierda: Tres familias de planos reticulares, con índices (110) en tres celosías equivalentes, mostrando una distancia desfasada entre ellas de 1/3 del espaciado interplanar en cada familia.
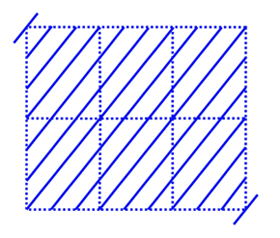
Derecha: El mismo conjunto de planos de la figura de la izquierda dibujado sobre una de las celosías equivalentes. Por lo tanto, sus índices Miller son (330) y su espaciado interplanar es 1/3 del espaciado interplanar de la familia (110).
Así, el concepto de índices Miller, previamente restringidos a tripletes numéricos (siendo números primos), ahora puede generalizarse a cualquier triplete de enteros. De esta manera, cada familia de aviones, “cubrirá” todo el cristal. Y por lo tanto, por cada punto del cristal podemos dibujar un número infinito de familias de planos con orientaciones infinitas.

A través de un punto en el cristal (en el ejemplo en el centro de la celda) podemos dibujar un número infinito de familias de planos con un número infinito de orientaciones. En este caso solo se muestran 3 familias y 3 orientaciones.
Por supuesto, las separaciones interplanares se pueden calcular directamente a partir de los índices de Miller (hkl) y los valores de los parámetros reticulares (ejes de celdas unitarias). La siguiente tabla muestra que estas relaciones pueden simplificarse para la métrica correspondiente de las diferentes celosías.

Fórmula para calcular las separaciones interplanares (d hkl ) para una familia de planos con índices Miller hkl en una celda unitaria de parámetros a , b , c , α , β , γ . Barras verticales (para el caso triclínico) significan la función “determinante”. En el caso trigonal a = b = c = A ; α = β = γ . En todos los casos, obviamente, el espaciado interplanar calculado también representa la distancia entre el origen de la celda y el plano más cercano de la familia.
Los lectores interesados también deberían echar un vistazo al capítulo sobre planos de celosía e índices Miller que ofrece la Universidad de Cambridge.
Y ahora algunos conceptos más sobre celosías: la llamada celosía recíproca...
Cualquier plano también se puede caracterizar por un vector (σ hkl) perpendicular a él. Por lo tanto, la proyección del vector de posición de cualquier punto (perteneciente al plano), sobre esa línea perpendicular es constante e independiente del punto. Es la distancia del plano al origen, es decir, el espaciado (d hkl).
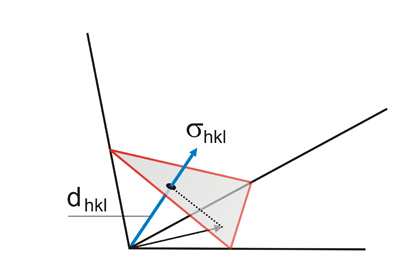
Cualquier plano puede ser representado por un vector perpendicular a él.
Considera la familia de planos hkl con la distancia interplanar d hkl. Del conjunto de vectores normales a la familia de los planos, tomamos el uno (σ hkl) con longitud 1/d hkl. El producto escalar entre este vector y el vector de posición (d' hkl) de un punto que pertenece a un plano de la familia es un entero (n), y este entero nos da el orden de ese plano en el familia hkl. Es decir: (σ hkl). (d' hkl) = (1/d hkl). (n.d hkl) = n (ver figura izquierda abajo)
n será 0 para el plano que pasa por el origen, 1 para el primer plano, 2 para el segundo, etc.
Así, σ hkl representa toda la familia de planos hkl que tienen un espaciado interplanar dado por d hkl. En particular, para el primer avión obtenemos: | σ hkl | d hkl = 1.

Si definimos 1/dhkl, como la longitud del vector σ hkl, el producto de este vector, multiplicado por el espaciado d hkl de la familia de planos es la unidad.
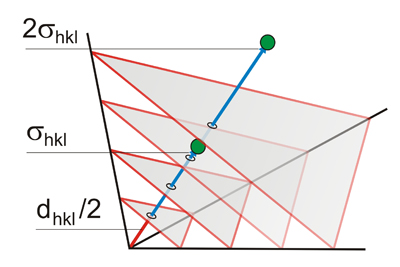
Si tomamos un vector 2 veces más largo que σ hkl, el espaciado interplanar de la nueva familia de planos correspondiente sería la mitad.
Si de este vector normal σ hkl de longitud 1/d hkl, tomamos otro vector, n veces (entero) más largo ( n. σ hkl), el producto mencionado anteriormente (| σ hkl | d hkl = 1 ) implicaría que el nuevo vector (n. σ hkl) correspondería a una familia de planos de índices nh, nk, nl que tiene un espaciado interplanar n veces menor. Es decir, por ejemplo, las longitudes de los siguientes espaciamientos interplanares llevarán la relación: d 100 = 2. (d 200) = 3. (d 300)..., de manera que σ 100 = (1/2). σ 200 = (1/3). σ 300 ... y de manera similar para otros aviones hkl.
Por lo tanto, parece que los módulos (longitudes) de los vectores perpendiculares (σ hkl) son recíprocos a los espaciamientos interplanares. Los puntos finales de estos vectores (flechas azules en la figura siguiente) también producen una celosía periódica que, debido a esta propiedad recíproca, se conoce como la red recíproca de la red directa original. Los puntos recíprocos obtenidos de esta manera (puntos verdes en la figura siguiente) se identifican con los mismos tripletes numéricos hkl (índices Miller) que representan los correspondientes familia de aviones.

Construcción geométrica de algunos puntos de una celosía recíproca (puntos verdes) a partir de una celosía directa. Para simplificar, asumimos que el tercer eje de la celosía directa (c ) es perpendicular a la pantalla. Las líneas rojas representan los planos reticulares (perpendiculares a la pantalla) y cuyos índices Miller se muestran en azul. Como ejemplo: el punto recíproco con índices (3,1,0) se ubicará sobre un vector perpendicular al plano (3,1,0) y su distancia al origen O es inversamente proporcional al espaciado de esa familia de planos.
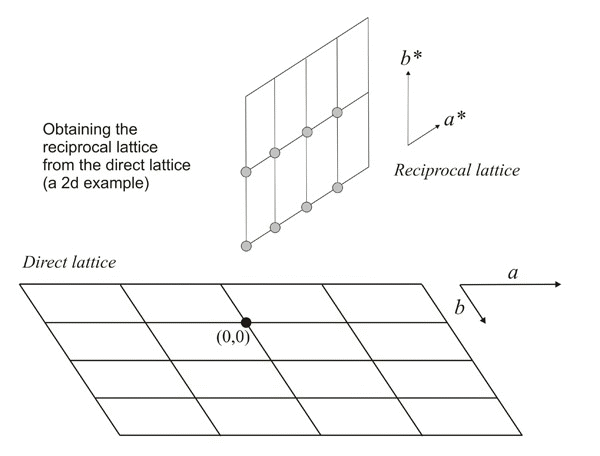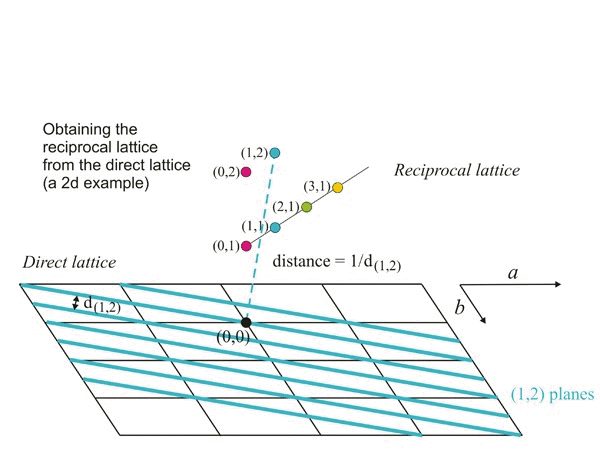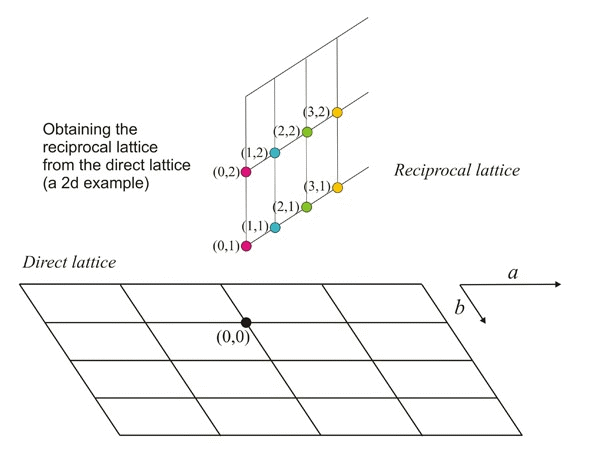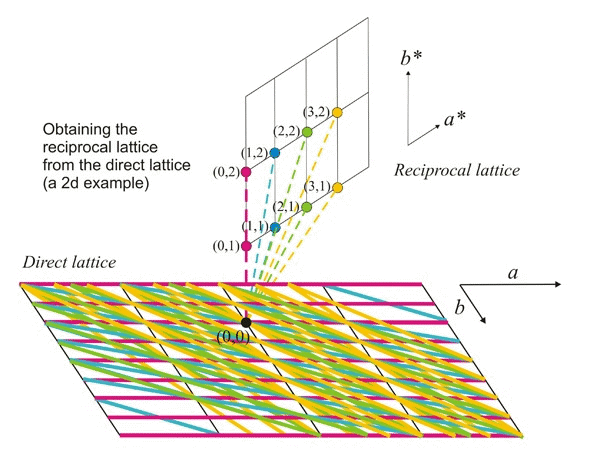
Ejemplo animado que muestra cómo obtener los puntos recíprocos a partir de una celosía directa
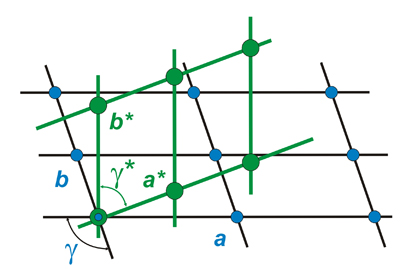
Ahora debería quedar claro que la celosía directa, y sus planos reticulares, están directamente asociados (enlazados) con la celosía recíproca. Además, en esta red recíproca también podemos definir una celda unitaria (celda unitaria recíproca) cuyas traducciones periódicas estarán determinadas por tres ejes recíprocos que forman ángulos recíprocos entre ellos. Si los ejes de las celdas unitarias y los ángulos de la celda directa son conocidos por las letras a, b, c, α, β, γ, los correspondientes los parámetros para la celda recíproca se escriben con los mismos símbolos, agregando un asterisco: a*, b*, c*, α *, β *, γ *. También debe quedar claro que estos ejes recíprocos (a*, b*, c*) corresponderán a los vectores σ 100, σ 010 y σ 001, respectivamente, de manera que cualquier vector recíproco puede expresarse como una combinación lineal de estos tres vectores recíprocos:
σ hkl = h a* + k b* + l c*
Vector de posición de cualquier punto recíproco

Relación geométrica entre celdas unitarias directas y recíprocas
La siguiente figura muestra nuevamente la fuerte relación entre las dos celosías (directa con puntos azules, recíproca en verde). En este caso, los terceros ejes recíprocos correspondientes (c y c*) son perpendiculares a la pantalla.
Y analíticamente la relación entre las celdas directa (= real) y recíproca puede escribirse como:
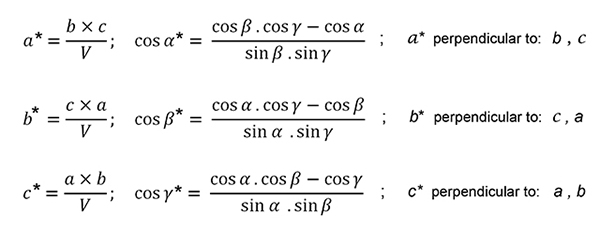
V = (a x b). c = a. b. c (1 - cos 2 α - cos 2 β - cos 2 γ + 2 cos α cos β cos γ) 1/2
Obsérvese que, de acuerdo con las definiciones dadas anteriormente, la longitud de a* es la inversa del espaciado interplanar d 100 (|a* | = 1/d 100), y eso | b* | = 1/d 010, y eso | c* | = 1/d 001. Por lo tanto, se pueden escribir los siguientes productos escalares (productos punto): a.a* = 1, a.b* = 0 y de manera similar con los otros pares de ejes.
Resumiendo:
- El espacio directo (= espacio real) es el espacio donde vivimos..., donde están los átomos..., donde crecen los cristales..., donde imaginamos las celosías directas (= celosías reales).
- El espacio recíproco es un espacio matemático construido sobre el espacio directo (= espacio real). Es el espacio donde se encuentran las celosías recíprocas, lo que nos ayudará a comprender los fenómenos de difracción cristalina.
- “Grande en el espacio directo (es decir, en el espacio real)”, significa “pequeño en el espacio recíproco”.
- “Pequeño en el espacio directo (es decir, en el espacio real)” significa “grande en el espacio recíproco”.
Además de esto, recomendamos descargar y ejecutar el applet Java de Nicolas Schoeni y Gervais Chapuis de la Ecole Polytechnique Fédéral de Lausanne (Suiza) para entender la relación entre celosías directas y recíprocas y cómo construir esta última a partir de una celosía directa . (Libre de cualquier tipo de virus).
Consulta también las páginas sobre el espacio recíproco que ofrece la Universidad de Cambridge a través de este enlace.
Y aunque estamos revelando aspectos correspondientes al siguiente capítulo (ver el último párrafo de esta página), el lector también debería mirar el video realizado por www.PhysicsReimagined.com, mostrando las relaciones geométricas entre directo y recíproco celosías, que se muestran a continuación como un gif animado:

El lector probablemente se esté preguntando por qué necesitamos este nuevo concepto (la celosía recíproca). Bueno, hay razones que lo justifican. Una de ellas es que una familia de planos puede ser representada por un solo punto, lo que obviamente simplifica las cosas. Y otra razón importante es que esta nueva celosía nos ofrece un modelo geométrico muy sencillo que puede interpretar los fenómenos de difracción en cristales. Pero esto se describirá en otro capítulo. ¡Vamos!


