9.3: Elasticidad del polímero y comportamiento de fuerza-extensión

La primavera entrópica

Para extender un polímero se requiere trabajo. Se calcula el trabajo reversible para extender la macromolécula a partir de la diferencia de energía libre de la cadena mantenida entre el estado inicial y final. Esto está naturalmente relacionado con la energía libre del sistema en función de la distancia de extremo a extremo del polímero:

\[w_{stretch} = F(r) - F(r_0) = - \int_{r_0}^{r} \vec{f_{rev}} \cdot d \vec{r} \nonumber\]

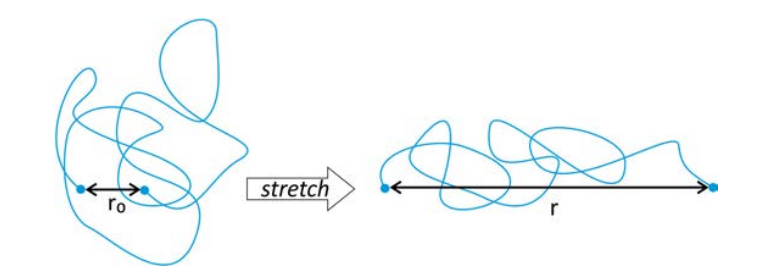
Para una cadena ideal, la energía libre depende únicamente de la entropía de la cadena:\(F = -TS\). Hay menos estados configuracionales disponibles para la cadena a medida que se estira a una extensión más grande. El número de estados configuracionales disponibles para el sistema se puede obtener calculando la función de partición conformacional,\(Q_{conf}\). Para estirar en una dimensión, la energía libre de Helmholtz es:

\[\begin{array} {rcl} {dF} & = & {-pdV - SdT + f\cdot dx} \\ {} & = & {-k_B T \ln Q_{conf}} \\ {S_{conf}} & = & {k_B \ln Q_{conf}} \end{array}\nonumber\]

\[f = - \left (\dfrac{\partial F}{\partial x} \right )_{V, T, N} = -k_B T \dfrac{\partial \ln Q_{conf}}{\partial x} = -T \dfrac{\partial S_{conf}}{\partial x} \label{eq9.3.1}\]

Cuando aumenta la distancia de extremo a extremo, disminuye el número de estados configuracionales disponibles para el sistema. Esto requiere una fuerza cada vez mayor a medida que la extensión se acerca a la longitud del contorno. Tenga en cuenta que se necesita más fuerza para estirar la cadena a mayor temperatura.

Dado que esta es una cadena unida libremente y todos los microestados tienen la misma energía, podemos equiparar la función de partición conformacional de una cadena en una extensión particular\(x\) con la densidad de probabilidad para las distancias de extremo a extremo de esa cadena

\[Q_{conf} \to P_{fjc} (r)\nonumber\]

Aunque estamos sosteniendo los extremos de la cadena fijos y estirando con los extremos restringidos a lo largo de una dirección (\(x\)), la función de distribución de probabilidad toma la forma tridimensional para dar cuenta adecuadamente de todas las configuraciones de cadena:\(P_{conf} (r) = P_0 e^{-\beta^2 r^2}\) con\(\beta^2 = 3k_B T/2n \ell^2\) y\(P_0 = \beta^3/\pi^{3/2}\) es una constante. Entonces

\[\ln P_{conf} (r) = -\beta^2 r^2 + \ln P_0 \nonumber\]

La fuerza necesaria para extender la cadena se puede calcular a partir de la eq. (\(\ref{eq9.3.1}\)) después de sustituir\(r^2 = x^2 + y^2 + z^2\), lo que da

\[f = -2\beta^2 k_B Tx = -\kappa_{st} x\nonumber\]

Entonces tenemos una relación lineal entre la fuerza y el desplazamiento, que es el clásico resorte de la Ley de Hooke con una constante de fuerza\(\kappa_{st}\) dada por

\[\kappa_{st} = \dfrac{3k_B T}{n\ell^2} = \dfrac{3k_B T}{\langle r^2 \rangle_0} \nonumber\]

Aquí\(\langle r^2 \rangle_0\) se refiere a la distancia cuadrática media de extremo a extremo para el FJC en ausencia de fuerzas aplicadas. Recuerda:\(\langle r^2 \rangle_0 = n \ell^2 = \ell L_C\). En el caso de que toda la fuerza restauradora se deba a la entropía, entonces llamamos a esto un resorte entrópico\(\kappa_{ES}\).

\[\kappa_{ES} = \dfrac{T}{2} \left (\dfrac{\partial^2 S}{\partial x^2} \right )_{N, V, T}\nonumber\]

Esto funciona para fuerzas pequeñas, mientras que la fuerza es reversible. Observe que\(\kappa_{ES}\) aumenta con la temperatura —como debería esperarse para las fuerzas restauradoras entrópicas.

Ejemplo: Estiramiento de ADN ¹

A baja fuerza:

dsDNA\(\to \kappa_{st} = 5\ pN/nm\)

ssDNA\(\to \kappa_{st} = 160\ pN/nm \to \text{more entropy/more force}\)

A mayor extensión te acercas asintóticamente a la longitud del contorno.

Fuerza/Extensión de un Polímero de Caminata Aleatoria

Derivamos el comportamiento de extensión de fuerza para un polímero de caminata aleatoria en una dimensión. La distancia de extremo a extremo es\(r\), la longitud del segmento es\(r\), y el número total de segmentos es\(n\).

Para cualquier dado\(r\), el número de configuraciones disponibles para el polímero es:

\[\Omega = \dfrac{n!}{n_+ ! n_- !}\nonumber\]

Esto se deduce de reconocer que la extensión de una cadena de paseo aleatorio en una dimensión está relacionada con la diferencia entre el número de segmentos que caminan en la dirección positiva,\(n_+\), y aquellos que caminan en la dirección negativa,\(n_-\). El número total de pasos es\(n = n_+ + n_-\). Además, la distancia de extremo a extremo se puede expresar como

\[r = (n_+ - n_-) \ell = (2n_+ - n) \ell = (n - 2n_-) \ell \label{eq9.3.2}\]

\[n_{\pm} = \dfrac{1}{2} \left (n \pm \dfrac{r}{\ell} \right ) \ \ \ \ \ \ \dfrac{\partial n_{\pm}}{\partial r} = \pm \dfrac{1}{2\ell}\nonumber\]

Entonces podemos calcular la energía libre de la cadena de caminar aleatoria que resulta de la entropía de la cadena, es decir, la degeneración de los estados configuracionales en cualquier extensión. Esto parece una entropía de cálculo de mezcla:

\[\begin{array} {rcl} {F} & = & {-k_B T \ln \Omega} \\ {} & = & {-k_B T (n \ln n - n_+ \ln n_+ - n_- \ln n_-)} \\ {} & = & {nk_B T (\phi_+ \ln \phi_+ + \phi_- \ln \phi_-)} \end{array} \nonumber\]

\[\phi_{\pm} = \dfrac{n_{\pm}}{n} = \dfrac{1}{2} (1 \pm x)\nonumber\]

Aquí la extensión fraccionaria de extremo a extremo de la cadena es

\[x = \dfrac{r}{L_C}\]

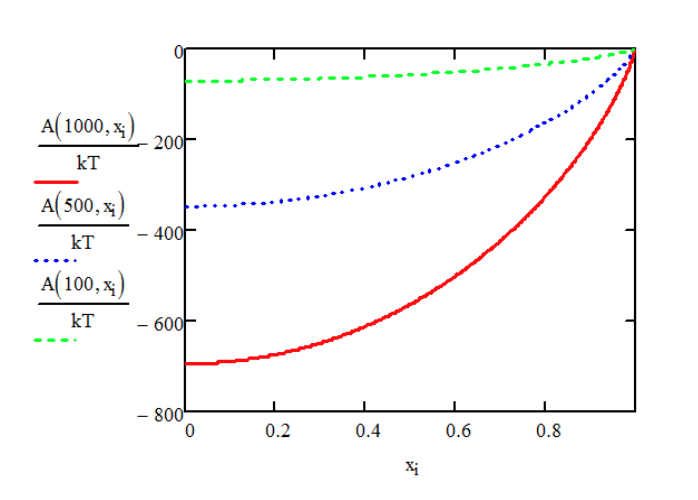
A continuación podemos calcular la fuerza necesaria para extender el polímero en función de\(r\):

\[f = -\dfrac{\partial F}{\partial r} \to \dfrac{\partial F}{\partial \phi_{\pm}} \dfrac{\partial \phi_{\pm}}{\partial r} \ \ \ \ \ \ \dfrac{\partial \phi_{\pm}}{\partial r} = \pm \dfrac{1}{2L_C} \nonumber\]

Usando eq. (\(\ref{eq9.3.2}\))

\[\begin{array} {rcl} {f} & = & {-nk_B T (\ln \phi_+ - \ln \phi_-) \left (\dfrac{1}{2L_C} \right )} \\ {} & = & {-\dfrac{nk_B T}{2L_C} \ln \left (\dfrac{1 + x}{1 - x} \right )} \\ {} & = & {-\dfrac{k_B T}{\ell} \dfrac{1}{2} \ln \left (\dfrac{1 + x}{1 - x} \right )} \end{array}\nonumber\]

\[f = -\dfrac{k_B T}{\ell} \text{tanh}^{-1} (x) \label{eq9.3.4}\]

donde\(I\) se utilizó la relación:\(\ln \left (\dfrac{1 + x}{1 - x} \right ) = 2 \text{tanh}^{-1} (x)\). Tenga en cuenta, aquí las fuerzas se escalan en unidades de\(k_B T/\ell\). Para fuerzas pequeñas\(x \ll 1\),\(\text{tanh}^{-1} (x) \approx x\) y eq. (\(\ref{eq9.3.4}\)) da\(f \approx \dfrac{k_B T}{\ell L_C} r\). Esto le da a Hooke el comportamiento de la Ley con la constante de fuerza entrópica esperada para una cadena 1D. Para una cadena 3D, esperaríamos:\(f \approx \dfrac{3k_B T}{\ell L_C} r\). Las escalas constantes de primavera con dimensionalidad.

La relación entre la posición, la fuerza y la función de partición

Ahora hagamos esto un poco más cuidadosamente. De la mecánica estadística clásica, la función de partición es

\[Q = \int \int dr^{3N} dp^{3N} \exp (-H/k_B T)\nonumber\]

Dónde\(H\) está el hamiltoniano para el sistema. El valor promedio para la posición de una partícula descrita por el hamiltoniano es

\[\langle x \rangle = \dfrac{1}{Q} \int \int dr^3 dp^3 x \exp (-H/k_B T)\nonumber\]

Si el hamiltoniano toma la forma

\[H = -f \cdot x \nonumber\]

Entonces

\[\langle x \rangle = \dfrac{k_B T}{Q} \left (\dfrac{\partial Q}{\partial f} \right )_{V, T, N} = k_B T \left (\dfrac{\partial \ln Q}{\partial f} \right )_{V, T, N} \nonumber\]

Esto describe la extensión promedio de una cadena si se aplica una fuerza a los extremos.

Comportamiento de fuerza/extensión para una cadena de unión libre

Haciendo uso de las expresiones anteriores y\(Q = q^N\)

\[q_{conf} = \int \int dr^3 dp^3 e^{-U/kT} e^{\vec{f} \cdot \vec{r}/k_B T} \ \ \ \ \ \ \ \langle r \rangle = Nk_B T \left (\dfrac{\partial \ln q_{conf}}{\partial f} \right )_{U, r, n}\nonumber\]

Aquí también insertamos un hamiltoniano general que da cuenta del potencial de interacción de la cadena interna y la fuerza ex la cadena:\(H = U - \vec{f} \cdot \vec{r}\). Para cadenas articuladas\(N\) libremente con n segmentos\(U \to 0\), establecemos y nos enfocamos en la fuerza ejercida en cada segmento de la cadena.

\[\vec{f} \cdot \vec{r} = \sum_{i = 1}^{n} \vec{f} \cdot \vec{\ell_i} = f \ell \sum_{i = 1}^{n} \cos \theta_i\nonumber\]

Tratando a los segmentos como independientes e integradores sobre todo\(\theta\), encontramos que

\[q_{conf} (f) = \dfrac{2\pi \text{sinh} \varphi}{\varphi} \nonumber\]

\[\langle r \rangle = n \ell \left [\text{coth} \varphi - \dfrac{1}{\varphi} \right ] \]

donde el parámetro de fuerza sin unidad es

\[\varphi = \dfrac{f \ell}{k_B T}\]

Como antes, la magnitud de la fuerza se expresa en relación con\(k_B T/\ell\). Tenga en cuenta que este cálculo es para la extensión promedio que resulta de una fuerza fija. Si queremos la fuerza necesaria para una extensión promedio dada, entonces necesitamos invertir la expresión. Tenga en cuenta que la forma funcional de la curva fuerza-extensión en eq. es diferente a la que encontramos para la caminata aleatoria 1D en eq. (\(\ref{eq9.3.4}\)). No esperamos la misma forma para estos problemas, ya que nuestro ejemplo de caminata aleatoria fue sobre una celosía cuadrada, y el FJC se propaga radialmente en todas las direcciones.

Derivación

Para una sola cadena de polímero:

\[\begin{array} {rcl} {q} & = & {\int \int dr^3 dp^3 e^{U/k_B T} e^{-f \cdot r/k_B T}} \\ {P(r)} & = & {\dfrac{1}{q} e^{-U/k_B T} e^{f \cdot r/k_B T}} \\ {\langle r \rangle} & = & {\dfrac{k_B T}{q} \left (\dfrac{\partial \ln q}{\partial f} \right )_u} \end{array}\nonumber\]

En el caso de la Cadena Libremente Articulado, juego\(U \to 0\).

\[\vec{f} \cdot \vec{r} = \vec{f} \cdot \sum_{i =1}^{n} \vec{\ell_i} = f \ell \sum_{i = 1}^{n} \cos \theta_i \nonumber\]

Segmentos desacoplados:

\[\begin{array} {rcl} {q} & \approx & {\int dr^3 \exp \left (\sum_i \dfrac{f \ell}{k_B T} \cos \theta_i \right )} \\ {} & = & {(\int_{0}^{2\pi} \int_{0}^{\pi} \exp [\varphi \cos \theta] \sin \theta d \theta d \phi)^n} \\ {} & = & {\left (\dfrac{2\pi \text{sinh} (\varphi)}{\varphi} \right )^n} \\ {\langle r \rangle} & = & {k_B T \dfrac{\partial}{\partial f} \ln q} \\ {} & = & {nk_B T \dfrac{\partial}{\partial f} \left [\ln \left \{\dfrac{2\pi \text{sinh} (\varphi)}{\varphi} \right \} \right ] \ \ \ \ \ \ \text{coth} (x) = \dfrac{e^x + e^{-x}}{e^x - e^{-x}}} \\ {\langle r \rangle} & = & {n \ell [\text{coth} (\varphi) - \varphi^{-1}]} \\ {\text{or } \langle x \rangle = \text{coth} (\varphi) - \varphi^{-1}} & \ & {\text{ The average fractional extension: } \langle x \rangle = \langle r \rangle / L_C} \end{array} \nonumber\]

Ahora veamos el comportamiento de la expresión para\(\langle x \rangle\) — también conocida como la función Langevin.

\[\langle r \rangle = n \ell [\text{coth} (\varphi) - \varphi^{-1}]\]

Mirando los límites:

• Fuerza débil\((\varphi \ll 1): f \ll k_B T/\ell\)
  Insertar y truncar la expansión:\(\text{coth} \varphi = \dfrac{1}{\varphi} + \dfrac{1}{3} \varphi - \dfrac{1}{45} \varphi^3 + \dfrac{2}{945} \varphi^5 + \cdots\), obtenemos
  \[\begin{array} {rcl} {\langle x \rangle} & = & {\dfrac{\langle r \rangle}{L_C} \approx \dfrac{1}{3} \varphi} \\ {\langle r \rangle} & \approx & {\dfrac{1}{3} \dfrac{n \ell^2}{k_B T} f} \\ {\text{or } \ \ \ f} & = & {\dfrac{3k_B T}{n \ell^2} \langle r \rangle = \kappa_{ES} \langle r \rangle} \end{array} \nonumber\]
  Obsérvese que este límite tiene la relación lineal esperada entre la fuerza y el desplazamiento, que se rige por la constante de resorte entrópica.
• Fuerza fuerte (\(\varphi \gg 1\)). \(f \gg k_B T / \ell\)Tomando el límite\(\text{coth} (x) \to 1\).
  \[\langle r \rangle \simeq n \ell \left [1 - \dfrac{1}{\varphi} \right ] \longleftarrow \lim_{f \to \infty} = \lim_{\alpha \to \infty} = L_C \text{ Contour length} \nonumber\]
  \[\text{Or } f = \dfrac{k_B T}{\ell} \dfrac{1}{1 - \langle x \rangle} \text{ where } \langle x \rangle = \dfrac{\langle r \rangle}{L_C} \nonumber\]
  Para un límite de fuerza fuerte, el comportamiento de extensión de fuerza se escala como,\(x \sim 1 - f^{-1}\).

Entonces, ¿cuál es el trabajo requerido para extender la cadena?

A fuerzas pequeñas, podemos integrarnos sobre el comportamiento lineal de fuerza-extensión. Bajo esas condiciones, para extender de\(r\) a\(r+\Delta r\), tenemos

\[w_{rev} = \int_0^{\Delta r} \kappa_{ES} r dr = \dfrac{3k_B T}{2n \ell^2} \Delta r^2\nonumber\]

Fuerza/Extensión de Cadena Tipo Gusano

Para el modelo de cadena tipo gusano, encontramos que la varianza en la distancia de extremo a extremo fue

\[\langle r^2 \rangle = 2 \ell_p L_C - 2 \ell_p^2 (1 - e^{-L_C/\ell_p}) \label{eq9.3.8}\]

donde\(L_C\) es la longitud del contorno, y la longitud de persistencia se relacionó con la constante de fuerza de flexión como\(\ell_p = \dfrac{\kappa_b}{k_B T}\). El comportamiento limitante para la eq. (\(\ref{eq9.3.8}\)) es:

\[\begin{array} {lclcrclcl} {\text{rigid:}} & \ \ & {\ell_p \gg L_C} & \ \ & {\langle r^2 \rangle} & \propto & {L_C^2} & \ \ & {} \\ {\text{flexible:}} & \ \ & {\ell_p \ll L_C} & \ \ & {\langle r^2 \rangle} & \sim & {2L_C \ell_p} & \ \ & {\therefore \text{for WLC}} \\ {} & \ \ & {} & \ \ & {} & = & {n_e \ell_e^2} & \ \ & {(2 \ell_p = \ell_e)} \end{array} \nonumber\]

Siguiendo un enfoque similar al FJC anterior, no es posible encontrar una solución exacta para el comportamiento de fuerza-extensión del WLC, pero es posible mostrar el comportamiento de extensión de fuerza en los límites rígidos y flexibles.

Configuración\(2\ell_p = \ell_e\) y uso de la extensión fraccionaria\(\langle x \rangle = \dfrac{\langle r \rangle}{L_C}\):\(\varphi = f\ell_e /k_B T\)

1. Fuerza débil (\(\varphi \ll 1\)) Comportamiento esperado de la Ley de Hooke
   \[f \ell_e \ll k_B T \ \ \ \ \ \ \ \ \ \ f = \dfrac{3k_B T}{\ell_e L_C} \longrightarrow \dfrac{f \ell_e}{k_B T} = 3\langle x \rangle \nonumber\]
   Para límite de fuerza débil, el comportamiento de extensión de fuerza se escala como,\(x \sim f\).
2. Fuerza fuerte (\(\varphi \gg 1\))
   \[f \ell_e \gg k_B T \ \ \ \ \ \ \ \ \langle r \rangle = L_C \left (1 - \dfrac{1}{2\sqrt{\varphi}} \right ) \longrightarrow \dfrac{f \ell_e}{k_B T} = \dfrac{1}{4(1 - \langle x \rangle)^2} \nonumber\]
   Para un límite de fuerza fuerte, el comportamiento de extensión de fuerza se escala como,\(x \sim 1 - f^{-1/2}\).

Una expresión aproximada para el resultado combinado (de Bustamante):

\[\dfrac{f\ell_p}{kT} = \dfrac{1}{4(1 - \langle x \rangle)^2} - \dfrac{1}{4} + \langle x \rangle\]

_____________________________

1. A. M. van Oijen y J. J. Loparo, Estudios de molécula única del replisoma, Anni. Rev. Biofys. 39, 429—448 (2010).